面向心血管疾病的自适应模块化神经网络预测模型

王振飞，陈金磊，郑志蕴，刘 冰

(郑州大学 信息工程学院，郑州 450001)

1 引 言

现代社会的日益发展使得人们的生活水平不断提高，原本的衣、食、住、行等一些基础性的需求已经不能满足人们对更高生活水平的追求.随之而来的是“健康”方面的问题越来越受到人们的重视.由于人们饮食方式的变化以及生活环境的污染，引起人们各种各样的健康问题，如罹患心脑血管等疾病的人群日益增多.心脏以及脑血管的疾病合称为心脑血管疾病，其病因一般为三高(即高血压、高血糖、高血脂)、动脉硬化和血液粘稠等.目前，由心脑血管病造成的死亡率不断上升，早发现，并在早期进行治疗，能很好的提高和保证病人的存活率，起到很好的预防效果[1].为了更好的提高心脑血管病人的存活率，不仅做到患病时的及时就医治疗，最为关键的是在未发病时的疾病预测和预防.心脑血管疾病及早地发现，是得到及早治疗的前提.因此，疾病风险预测研究是非常有意义的课题.

KL Chien等人利用台湾的一组中风病人数据，构建了一个预测中国成年人中风发病率的模型[2]，林倍倍等人通过探索上海社区群众的糖尿病发病状况，为在社区进行糖尿病防治工作提供依据[3].在机器学习领域，袁莺楹等人通过时间序列、神经网络等算法在进行疾病的预测[4].庞显涛等人使用了将多种机器学习模型相结合的方法来对疾病的发生进行预测，其将神经网络与遗传算法相结合提高了预测准确率[5].崔霞等人提出了SRGM模型组合算法，可以提升预测准确度[10].RBF神经网络具有很好的全局最优特性，不容易陷入局部极小值以及容错性高的特点[11]，但是针对心脑血管疾病预测，数据维数高和数据之间关系复杂的问题，RBF神经网络还存在着训练耗时长，训练结果达不到预期等一些问题.为了克服单一前馈神经网络的局限性，研究人员提出模拟人的大脑在分析处理问题时功能分区的模型，将一种模块化的方法融入其中，把一个相对较为复杂的问题，转化为多个较为简单的问题，运用“分而治之”的思想，单独的子模块能够处理接收到的较为简单的问题[6]，这种学习方式的优点是可以因问题特点实施不同网络结构学习复杂问题[7].本文针对心脑血管疾病这种复杂问题提出一种自适应模块化神经网络结构模型(Adaptive Modular Neural Network，AMNN).首先采用密度峰值聚类方法，找出数据集的聚类中心，以此确定每个子模块的训练样本集，然后每个模块采用BP神经网络算法，该算法能根据分配来的训练样本自适应构建模块结构，模块的网络结构由本身的学习任务自适应确定.最后以河南某地6000余名农村居民常见心血管代谢性疾病及健康影响因素体检问诊单为数据集，实验验证AMNN的性能.

2 自适应模块化神经网络(AMNN)

2.1 AMNN结构原理

AMNN的网络结构如图1，其与一般的BP神经网络有所不同，AMNN先对数据进行处理，利用模块化的思想将复杂问题分类研究.AMNN含有多个模块，其工作方式是，首先在数据处理阶段对不同的训练样本进行聚类分析，将数据样本分为多个类，根据聚类分析的结果，选择AMNN 中相应的模块进行学习.每个模块单元中为BP神经网络模型，其各层参数及学习率由样本数据聚类后分配来的不同的训练样本进行自适应构建，其任务是学习分配来的训练样本.

AMNN的工作流程和功能模块设计是将数据集进行聚类分析确定聚类中心、根据聚类结果将子数据集选择相应的子网络进行学习、子网络由匹配来的子数据集自适应的确定自己的训练参数.

2.2 任务分解

在数据输入后，任务分解的目的就是将整个数据样本空间通过聚类的方法归为若干个子数据样本空间.新的子数据样本空间中的数据被送入相应的子网络中.子样本空间的数目与子网络的数目一致.

本文借鉴Alex Rodriguez等人提出的点密度峰值聚类算法[8]，该算法可以确定训练样本聚类中心的数目，从而确定子网络的数目.该算法在如何确定聚类中心上有十分经典的研究，确定聚类中心的理论依据是，确定数据集聚类中心需要同时满足两个约束：第一，训练样本聚类中心的局部密度需要足够大，即聚类中心的“邻居”的局部密度都不超过其局部密度；第二，某个聚类中心与另外的局部密度相对较大的数据点的距离足够远.点密度峰值聚类算法的原理可以使用两个参量来描述，ρi和δi，其中数据点i的局部概率密度用ρi表示，δi表示数据点i与另外具有更高局部密度数据点之间的最小距离.

由此，设输入的训练样本集为S={(xk，yk)，k=1，2，…，N}，对于S中的任意数据样本，ρi和δi的定义为：

(1)

(2)

式(1)(2)中，dij=dist(xi，xj)代表两个样本点xi和xj之间的距离，此距离为欧式距离，dc为截断距离，其值大于0.dc的选取对算法的结果有较大的影响，如果取值过大，会造成ρi的值很大，区分度不高，极端情况下的取值所有数据点都归于一类；如果取值太小，会使一个类被分为两个类或多个类，因此dc的选值就十分重要，本文将所有两点间的距离dij进行升序排序，取前2%的值，四舍五入作为dc值，从某种程度上，降低了参数对具体问题的依懒性.

本文所用的点概率密度峰值聚类算法具体算法描述如下.

算法1.确定数据集的聚类中心

1.对数据集的预处理工作

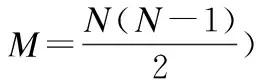
2.计算ρi，(i=1，2，…，N)，令ρi由大到小排列；

3.计算δi，(i=1，2，…，N)，令δi由大到小排列；

4.令γi=ρiδi，由此生成决策图得到聚类中心.

由算法1得到的数据集聚类中心是{c1，c2，…，cF}，共得到F个聚类中心，时间复杂度为O(n2).基于该算法得到的聚类中心，数据集中的所有样本点针对各个聚类中心生成模糊集，生成模糊集依赖公式(3)，共建立个F个模糊集：

(3)

其中，fik
表示训练样本xk隶属于第i个模糊集的模糊隶属度.指数部分分子表示样本xk与聚类中心ci的距离，分母的选取是为了扩大数值，从而提高模糊隶属度的辨识率，分母过大会造成隶属函数过于平缓，隶属度区分度不大，分母过小会使隶属函数过于“尖锐”和“陡峭”，会造成结果趋近于0的情况，从而无法分辨隶属度，由实验得到，分母选取0.02较为合适.对于数据集中的每个样本点，如果xk距离聚类中心ci越近，那么xk对于ci的隶属度就越高，并将xk归入相应的子样本空间，输入子网络进行学习.

2.3 子网络训练参数的自适应确定

AMNN 中的子网络为BP神经网络，误差反向传播与正向传播方向相反，其先从输出层开始由隐层到达输入层，依次层层返回，根据误差值修改各层单元联结权值，对以上过程描述如下.

(4)

联结权值的修改按公式(4)计算.

wjk(t+1)=wjk(t)+Δwjk

(5)

BP算法采用梯度下降方向修改联结权值，权值变化量为

(6)

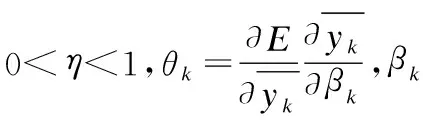
(7)

对于隐层有

(8)

BP神经网络的学习训练过程是在正向与反向传播作用下，不断修改各层单元权值的一个反复过程，直到实际输出达到要求精度或者达到最大训练次数.

算法2.模块自适应神经网络算法

1.依据算法1聚类分析划分的子样本集，将样本分配给对应子模块Qi；

2.由子模块Qi计算得出训练结果yk，并由误差函数公式(4)计算出误差E；

3.由输出层权值更新公式(7)与误差E，计算出输出层权值wjk；同理，由隐含层权值更新公式(8)与误差E，计算出隐含层权值vij；

4.重复步骤(1)，计算出新的权值wjk与vij.

利用上述算法1实现样本分类以及算法2实现模块的权值自适应算法，计算出每层权值，从而实现权值自适应调整，不需人工干预.

3 实验分析

3.1 数据来源

本文采用的数据来源于河南某地6000余名农村居民心血管代谢性疾病及健康影响因素体检问诊单数据集.

数据属性包括：年龄，性别，血压，饮酒状况，吸烟状况，睡眠状况，家族遗传史，心电图监测，BMI指数.实验通过对数据的预处理，将源数据进行加工处理，剔除其中的不合理数据，提高数据的准确性，将经过预处理之后的数据引入新的数据集中，为本论文所用的数据.所用数据选取80%为学习数据，20%为测试数据.

3.2 数据的归一化处理

由于数据集中每个属性所表示的含义不同，数量级也不尽相同，因此需要对使用到的数据采用一定预处理方法，从而减少或消除不同数据属性之间量级的差异而产生的影响，这种方法就是归一化方法.经过数据归一化后，数据值的范围在[0，1]之间.

本文采用Z-score方法对所用数据集进行归一化处理，采用该方法得到的数据呈正态分布，其所用转换原理是通过均值和标准差对数据样本进行处理，其原理如公式(9)所示.

(9)

其中μ是数据样本的平均值，σ是数据样本的标准差，首先计算出数据样本的均值，再根据公式(10)得出数据样本的标准差.

(10)

其中N为数据样本的个数，μ是平均值.最后进行数据的归一化处理，得出新的数据.

3.3 实验结果与分析

实验所用数据的属性如表1所示，其中年龄，血压，睡眠状况，BMI指数数据需要进行归一化处理.

表1 信息属性表Table 1 Information attributeTable

提取测试数据库中已经处理好的数据，利用已经训练好的预测模型，对人员发病情况进行预测，并与传统BP神经网络(BPNN)和标准的随机森林(RF)进行对比.得到如图2和图3所示结果.

图2 三种模型不同年龄的识别率对比图Fig.2 Comparison diagram of recognition rate of three models at different ages

从图2和图3可以明显看出模块化神经网络的预测正确率要比RF和传统的BPNN精确率有所提高，特别是在45-50年龄段，心血管代谢性疾病高发期，AMNN优势更明显.

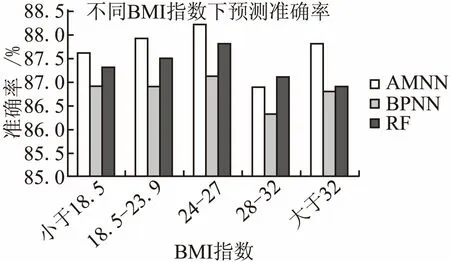
图3 三种模型关于BMI指数的识别率对比图Fig.3 Comparison of recognition rates of three models with respect to the BMI index

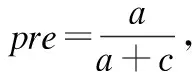
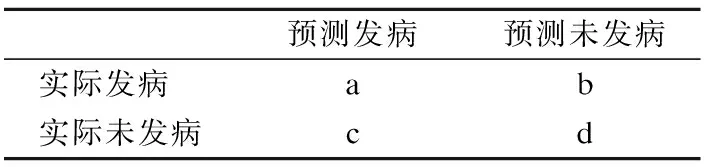
表2 混淆矩阵表Table 2 Confusion matrixTable

实际上数据可能会存在一定的不平衡性，我们使用F-value和G-mean的方法来进行预测结论的考察.

(11)

F-value能更好、更真实的对预测结果进行评估，如公式(11)，其中λ取值为正.如果λ≥1，那么说明查全率对评估带来主要的作用；反之，如果λ<1，说明查准率在评估过程中有主要影响，这里我们取1.

(12)

G-mean维持了数据在不平衡状态下时，预测结果的精度.

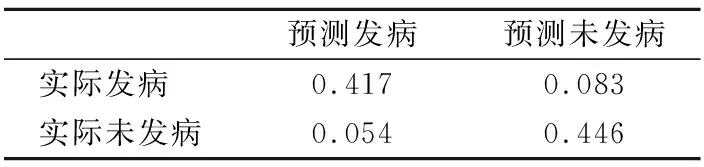
表3 测试数据库的混淆矩阵Table 3 Confusion matrix of test database

表4 F-value值和G-mean值(%)Table 4 F-value values and G-mean values (%)

表3表示对测试数据库内的人员信息进行预测之后结果的混淆矩阵，从表中我们可以得出，预测未发病但实际发病的概率和预测发病但实际未发病的概率都很低，这说明了神经网络模型对心脑血管疾病预测的准确度十分良好.表4表示的是心脑血管疾病发病的F-value和G-mean值.

4 总结和展望

为解决BP神经网络处理心脑血管疾病复杂问题的不足，提出一种自适应模块化神经网络模型，该模型采用点密度峰值聚类算法确定数据集的聚类中心个数，从而确定子网络的数目，每一个子网络采用BP神经网络算法，该算法可以由子数据集自适应确定训练参数，不需要人工参与；最后利用农村居民常见慢性病及健康影响因素体检问诊单数据集进行性能验证，与标准的随机森林和传统单一神经网络分类方法相比有效的降低了计算复杂度，提高了预测精度.

由于心脑血管疾病的种类繁多，病因复杂，因此进一步的研究可以关注于增加心脑血管疾病的属性个数，提高聚类算法精度来提高预测准确的概率.