基于Markov链修正的铁路运量灰色组合预测模型研究

贾鼎元,柴乃杰,王恩茂

(兰州交通大学土木工程学院,兰州 730070)

伴随着社会经济学理论、数学分析方法以及计算工具的不断完善和提高，人们对经济预测准确性的要求和需要也越来越高[1]。目前传统预测手段主要分为定性预测与定量预测两大类[2-3]。定性预测包括：市场调查法、类比法和专家调查法。定量预测方法按形成成因，大致可分为以因果关系和以时间序列为参数的2种预测方法，根据现有情况的需要，以时间序列为参数的预测方法的研究占绝大多数。基于时间参数的预测方法是将近年来实际客运量数据按照时间的顺序排列，通过对其反复训练与拟合，建立具有一定规律性的数学模型，并向外进行推算。目前比较有代表性的指数平滑法、线性回归法、灰色预测法、BP神经网络以及支持向量机等[4-9]，这些方法在本质上都是建立在原始数据的拟合模型，通过模型本身的反复训练，最大限度地提高自身的拟合精度。然而，以上这些方法各自也都或多或少地存在局限性，而且每一种模型都有不同的适用范围。所以，仅有弥补原单一模型自身的缺陷，才能取得更加精确的预测结果，否则仍然无法保证所得预测结果的准确性。

铁路客运量是一个受社会、经济等多种因素影响的复杂系统[10-11]。而传统的单一客运量预测模型由于自身缺陷与应用的局限性，已越来越无法适应复杂的客运量预测系统。因此，为了弥补原单一预测模型的不足，本文将引入灰色GM(1，1)[12]与灰色Verhulst[13]组合模型，这使得预测对象必须首先满足以下基本两点：(1)数据要求满足属于灰色系统范畴，多为离散时间序列；(2)要求数据无后效性。为能使这两种模型进行有机地集成，以达到有效地提高预测精度的目的，故采用信息熵中的熵权法。熵权法一方面可以充分地利用相对误差数据本身的效用值，另一方面还可有效地减少专家主观因素的影响。最后，运用Markov链方法对熵权法灰色组合预测模型的拟合值进行修正，使之能够将预测结果由单一数值修正成为预测年份的客运量区间，而且还可以有效估算出该区间产生的概率情况，增加了预测的可信度。

1 熵权法灰色组合模型的基本思路

1.1 灰色GM(1，1)模型的基本思路

灰色预测模型的基本思路是将部分已知的数据序列通过训练、拟合，寻找出一种具有某种规律的动态化数学函数。然后按照某种准则，反复修正提高白化度，直到达到期望的预测效果为止。其基础是建立模型，通常为一阶单变量模型GM(1，1)和一阶多变量模型GM(1，N)[14]。尤其是GM(1，1)模型，应用十分广泛。

GM(1，1)模型是一阶单变量线性微分方程，其离散形式为

(1)

式中，a、u为待识别的灰色参数。

计算式(1)中一阶单变量的线性微分方程的解，即为

(2)

其中

(3)

(4)

式中，k=2，3，…，n。

以上为GM(1，1)模型的基本公式和思路，其中称式(4)为GM(1，1)模型的基本结论。

1.2 灰色Verhulst模型的基本思路

设X(0)为原始数据序列，X(1)为X(0)的一次累加生成1-AGO序列，即

X(0)=(x(0)(1)，x(0)(2)，…x(0)(k)，…，x(0)(n))

(5)

X(1)=(x(1)(1)，x(1)(2)，…x(1)(k)…，x(1)(n))

(6)

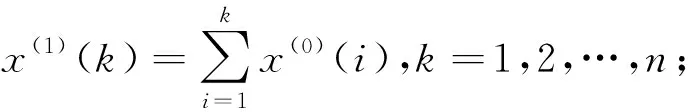
Z(1)为X(1)的紧邻均值生成序列，即

Z(1)=(z(1)(1)，z(1)(2)，z(1)(3)，…，z(1)(n))

(7)

其中，Z(1)(1)=X(1)(1)

则称式：

x(0)(k)+az(1)(k)=b(z(1)(k))α

(8)

为GM(1，1，α)幂模型[15]。

将式(8)进一步转化为

(9)

称为GM(1，1，α)幂模型的白化方程。

求得式(9)中GM(1，1，α)幂模型白化方程的解为：

(10)

当α=2时，则称式

x(0)(k)+az(1)(k)=b(z(1)(k))2

(11)

为灰色Verhulst模型。

称式：

(12)

为灰色Verhulst模型的微分方程。

对于式(12)中灰色Verhulst微分方程的解为

(13)

故离散型灰色Verhulst模型的预测模型为

(14)

1.3 组合预测模型

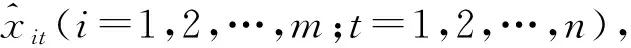
(15)

1.4 熵权法组合预测模型权系数的确定

组合预测是指通过合理的权系数将各种单一预测方法进行集成，以期望获得更加准确的预测结果，但目前最主要的问题就是如何求得恰当的权系数。通过分析，本文将借助信息熵理论[17-18]，根据不同预测方法相对误差的变异程度，确定组合预测中的各单一模型的权系数。

(1)设第t时刻的第i种预测方法相对误差为

(16)

(2)对预测相对误差进行归一化处理，即

(3)计算第i种预测方法的熵值Hi

(18)

因此，对第i种预测方法而言，如果fit全部相等，即fit=1/n，t=1，2，…，n。那么Hi取得极大值1，则有0≤Hi≤1。

(3)计算第i种预测方法的变异程度系数

vi=1-Hi，i=1，2，…，m

(19)

(4)确定第i种预测方法的权系数

(20)

(5)建立组合预测模型

(21)

1.5 Markov链方法对预测结果修正的基本思路

由于灰色组合模型的预测结果通常是一个单一的粗糙数值，这就容易产生较大的误差。为了减少误差，将组合模型的预测值拓展到一个较小的范围之内，故利用Markov链方法对灰色组合预测模型结果的修正，即将预测的结果由一个单一的数值修正成为预测年份的客运量区间，同时估算出该区间产生的概率情况[19-20]。

Markov链方法的核心环节是求得原始数据序列的一步状态转移矩阵。即设样本中状态Si出现的mi次，由状态Si转移到状态Sj的次数为mij，则一步转移概率的近似值为

Pij=mij/mi

(22)

式中，Pij为由Markov链状态Si转移到状态Sj的概率。

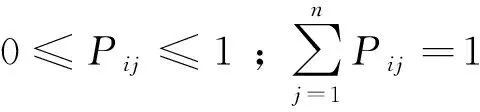
(23)

综上，构造一步状态转移矩阵形式为

(24)

针对熵权法组合模型所得到的预测结果，可通过式(22)～式(24) Markov链方法，获得该组合模型在已知年份的偏差规律，以此对所得预测结果进行修正，即由一个单一的粗糙预测数值修正成为区间和概率组成的预测范围，从而增加了预测的可信性。

2 实例分析

为验证基于Markov链修正的一种灰色组合预测模型应用的有效性和可靠性，以2004年～2015年甘肃省铁路客运量为例进行实证预测，如表1所示。

表1 2004年～2015年甘肃省铁路实际客运量及符号

2.1 GM(1，1)预测

以表1中所选取的2004年～2015年共12年的甘肃省铁路客运量原始数据为数据，并作符号标记。分别采用灰色GM(1，1)模型和灰色Verhulst对其进行拟合，具体拟合过程如下。

根据表(1)及式(1)、式(2)的GM(1，1)模型基本思路和公式，可得

B=

由此得到a=-0.079 4，u=1 239.768，所以u/a=-15 614.206 6。进一步计算得到甘肃省2004年～2015铁路客运量的灰色GM(1，1)预测式

同理，根据式(5)～式(14)得到甘肃省2004年～2015年铁路客运量的灰色Verhulst预测式

最后，根据灰色GM(1，1)和灰色Verhulst预测式分别计算甘肃省2004年～2015年铁路客运量的预测值，并将此两种模型的预测结果进行对比，如表2所示。其中，误差幅度(记为εt)计算公式为

i=1，2，…，m;t=1，2，…，n

(25)

表2 2005年～2015年两种预测方法结果对比

2.2 基于熵值法确定权系数的组合预测模型

在运用以上两种单一预测模型计算出预测拟合值后，根据熵值法的原理，利用式(17)～式(20)来确定两种单一预测模型的组合权系数，即得到的权系数向量为

ω=(0.689 3， 0.310 7)

从而得到相应的熵值法组合模型为

2.3 不同预测方法的精度比较

以预测值的平均相对误差作为衡量预测精度的指标，来比较各种预测模型的预测准确性。即通过分别计算两种单一预测模型和熵权法组合模型的平均相对误差，结果见表3，可以得出，熵值法组合预测模型精度明显高于两种单一预测模型的精度。其中，预测平均相对误差公式[1]为

同时，为更加直观地反映出该4种模型得出的模拟值与实际值的对比情况，绘制出图1加以说明。

表3 3种预测方法的平均相对误差

图1 3种预测模型拟合曲线

下面将运用Markov链方法对熵权法灰色组合模型的预测值进行修正。

2.4 Markov链方法对预测值进行修正

根据式(22)～式(24)Markov链分析方法的实际情况，同时对比年实际铁路客运量的数值，将熵权法灰色组合模型的预测结果划分为3种状态。

状态1 呈现预测高估状态，即残差(实际值减去预测值的差)占实际客运量的比例小于-15%、大于-5%。在12年之中仅有5年(2005、2006、2012、2013、2014年)呈现这种状态。

状态2 预测评估较为准确，即残差占实际客运量的比例在-5%～5%，可以称之为正常状态，在12年之中仅有2年(2007年、2015年)呈现这种状态。

状态3 呈现预测低估状态，即评估残差占实际客运量的比例在5%～15%。在12年中有5年(2008年～2011年、2016年)呈现出这种状态。

根据以上分类标准，可获得2005年～2015年各状态出现的情况，如表4所示。

然后，根据式(22)可得其一步转移频数矩阵M，从而构造出一步状态转移概率矩阵P(1)，即

同理，依次得出

P(n)=(P(1))n

表4 2005年～2015年组合模型的预测值及状态分类

根据马尔可夫链修正原理，在得到熵权法组合预测模型的预测值及状态划分之后，可由此推算出未来6年(2016年～2021年)的预测状态向量，如表5所示。

由表5可得，利用组合预测模型所得2016年、2017年的预测客运量分别为3 292万人和3 572万人，而查阅甘肃统计年鉴该两年的甘肃铁路实际客运量分别为3 353万人和3 604万人。通过两者对比发现，单一预测结果略微偏低，而与表5中预测年度的概率最大的状态均为一般状态(E2)的预测区间结果完全吻合，即2016年和2017年客运量分别为[3 128.335 8，3 457.634 4)和[3 393.486 5，3 750.695 6)，进一步验证了预测结果的准确性。同时，也表明在未来的4年内甘肃省铁路客运量将呈逐渐上升趋势，预测年度的概率最大的状态均为正常状态(E2)，最大的可能概率分别为80%、69%、62.95%、59.62%、57.79%、56.79%；其次的概率最大的是低估状态(E3)，即实际发生值会高于由灰色模型预测结果区间，其概率分别为20%、31%、37.05%、40.38%、42.21%、43.21%，而预测高估状态(E1)的概率却为0%。因此，从总体上来讲，由灰色预测得到的结论往往会偏低于甘肃省的实际铁路客运量，即预测未来几年内甘肃省铁路客运市场会向更加兴旺的方向发展。事实证明，对于铁路运量的预测问题来说，Markov链修正的熵权法灰色组合预测方法更加有助于铁路部门对未来客运量发展趋势作出判断。

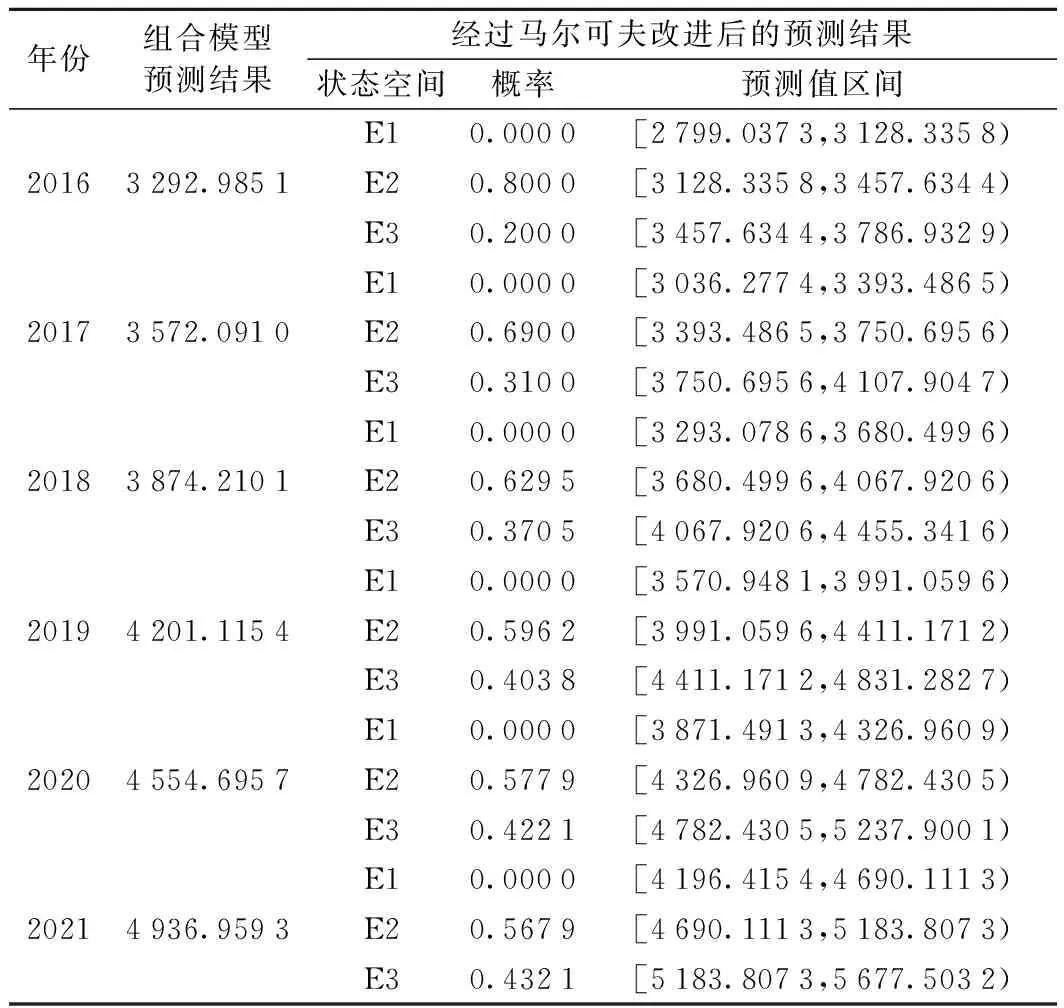
表5 2016年～2021年基于Markov链方法修正的预测结果

3 结论

通过对Markov链修正的熵权法灰色组合预测模型的研究，为改进预测模型的研究又提供了一种可行的思路，并得出如下结论。

(1)该方法的适用对象数据必须同时满足灰色GM(1，1)模型和Verhulst模型两种单一预测方法的要求，即既要满足灰色系统的范畴，多为离散时间序列，又要具有无后效性的特征。

(2)根据GM(1，1)和Verhulst两种单一预测方法所得的相对误差变异程度，运用信息熵理论确定各自的权系数，并对两种方法进行集成，能有效地提高预测精度。

(3)采用Markov链方法对熵值法灰色组合预测方法的拟合值进行修正，既能实现将预测结果由一个单一的粗糙数值修正成为预测年份的客运量区间，同时还能有效地估算出该区间产生的概率情况。

(4)根据预测中值和最大状态概率，推算和把握未来几年内经济现象的总体发展趋势，为决策者的经济行为提供重要的依据。