某面板堆石坝防渗墙内力与变形特性研究

谢江松，王政平，湛 杰

(中水珠江规划勘测设计有限公司，广东 广州 510610)

面板堆石坝的防渗体系关系到坝基稳定和大坝的安危，防渗体系的合理设计是大坝成功建设和运营的关键因素之一[1]。混凝土防渗墙作为大坝防渗体系的主体部分，其应力变形一直是结构设计关注的重点。

防渗墙在进行强度设计和配筋计算时，常常需要知道防渗墙的内力大小及其分布[2]。目前，对受力明确、结构简单的防渗墙强度设计一般采用解析法，按设计规范[3]的公式简化计算。该法使用方便、快捷，得到了广泛的运用；但在防渗墙受力复杂、非线性特征明显时受限，如覆盖层深厚、地层岩性差异较大的情况下，防渗墙受力复杂，且呈明显的非线性特征，此时采用解析法难以得到防渗墙的内力分布情况，必须考虑其他方法和手段。

20世纪80年代以前，郑秀培[4]等人将防渗墙视为地基梁，然而其计算结果和实测数据相差较远。近十几年来，随着岩土工程有限元技术日益成熟，为复杂防渗墙的应力和位移分析提供了更科学、可靠的手段。目前国内一些重要的大坝和围堰工程都采用数值手段分析和评价防渗墙的应力和位移，如程展林[5]利用数值方法对三峡二期围堰混凝土防渗墙的应力应变进行了分析，在假定防渗墙为弯压结构的前提下，给出了防渗墙应变、变形的分布规律；胡黎明[6]对三峡二期围堰抽水期与运行期防渗墙应力特性和变形进行了分析；郦能惠[7]采用多种本构模型计算了冶勒水电站大坝防渗墙的应力变形性状。

现有的研究多集中在防渗墙的应力和变形，而对于防渗墙的内力分布鲜有探讨，不能对防渗墙直接进行强度设计和配筋计算。本文以阿根廷奈斯托尔·基什内尔总统水电站工程为例，采用有限元法先分析完建情况、蓄水情况和地震情况下防渗墙结构应力变形特征，得到墙体的位移和节点刚度矩阵后，再通过有限元内力法[8]得到墙体的内力值，分析和研究深厚冲积层中混凝土防渗墙变形与内力分布特性，为类似工程防渗墙的设计和计算提供参考。

1 工程概况

某水电站位于阿根廷南部圣克鲁斯河，水库总库容58亿m3，多年平均发电量约为3 167 GW·h，为大(1)型工程。拦河坝为混凝土面板堆石坝和混凝土重力坝的混合坝型，坝顶全长约2 044 m，其中面板堆石坝长1 616 m，正常运行水位176.5 m，坝顶高程180.6 m，最大坝高73.3 m。大坝建筑级别为1级。

坝址河谷宽阔，坝基覆盖层为第四系松散冲积物，厚度25～35 m，主要由冰碛、冰水沉积、冲积及崩坡积物等组成；冲击层下部所处区域地层以第三系(Monte Leon组)粉砂岩及火山凝灰岩等沉积岩为主。基础防渗采用混凝土防渗墙+帷幕灌浆。防渗墙厚0.8 m，高47 m，上部10 m位于坝体填筑料内，坝体以下30 m为河床冲积层，防渗墙底部嵌入弱风化岩层7 m。

大坝建筑物级别高，工程量大，因此，对防渗墙的精准分析和研究对大坝的安全性和经济性具有十分重要的意义。

2 计算理论

采用有限元内力法，利用节点位移和节点刚度矩阵求解截面内力。其中，防渗墙的土压力和水压力由流固耦合计算得到。

对于某一结构系统，若用给定的截面π将结构分为1、2两个部分，并对这两个部分在制定界面上施加1组大小相等，方向相反的约束内力，则可建立平衡方程为：

(1)

式中i——非π截面上的节点；j——截面π上的节点；Fi——非π截面上节点荷载向量；Fj——截面π上节点荷载向量，{fj}1、{fj}2——π截面上1、2两个子结构之间的约束内力，有：

{fj}1+{fj}2=0

(2)

由于上面2个公式完全等价，则由有限元平衡方程解出节点位移后代入上式即可直接求解给定截面π上的约束内力：

{fj}1=-{fj}2=

[Kji]1{δi}1+[Kjj]1{δj}1-{Fj}1=

{Fj}2-[Kji]2{δi}2-[Kjj]2{δi}2

(3)

通过处理截面上网格单元信息和节点信息，再将求得的约束内力值合成为结构内力值[9]。

3 计算方案

3.1 有限元计算模型

面板堆石坝长1.6 km，且河床平坦无明显起伏变化，因此，按平面应变问题进行分析可满足精度要求。

根据设计方案和地质资料建立二维平面应变网格模型(图1)。防渗墙单元尺寸为0.2 m，坝体单元尺寸为0.2～1 m，地基单元尺寸为0.2～5 m。全模型共28 628个单元，42 288个节点。混凝土结构与坝体填筑料、冲积层之间因材料特性差异较大，因此，在面板、趾板和防渗墙之间,以及面板与大坝垫层和铺盖、趾板与基础、防渗墙与地基之间均采用接触算法,设置Goodman接触单元(图2)。

3.2 计算参数

采用有限元法计算土石坝应力与变形特性时，中国规范推荐采用E-B、K-G和双屈服面弹塑性模型[10]。本工程原设计单位按美国规范[11]采用摩尔-库伦模型对大坝应力与变形进行了分析；由于缺少E-B等模型试验参数，同时为了便于与原设计单位成果的对照和分析，本文对坝体也采用摩尔-库伦模型。坝体各材料计算参数见表1，坝基计算参数见表2。

表1 坝体材料力学参数

3.3 计算工况

水库最高水位为176.5 m，参照美国规范[11]，计算考虑3种主要控制工况，见表3。

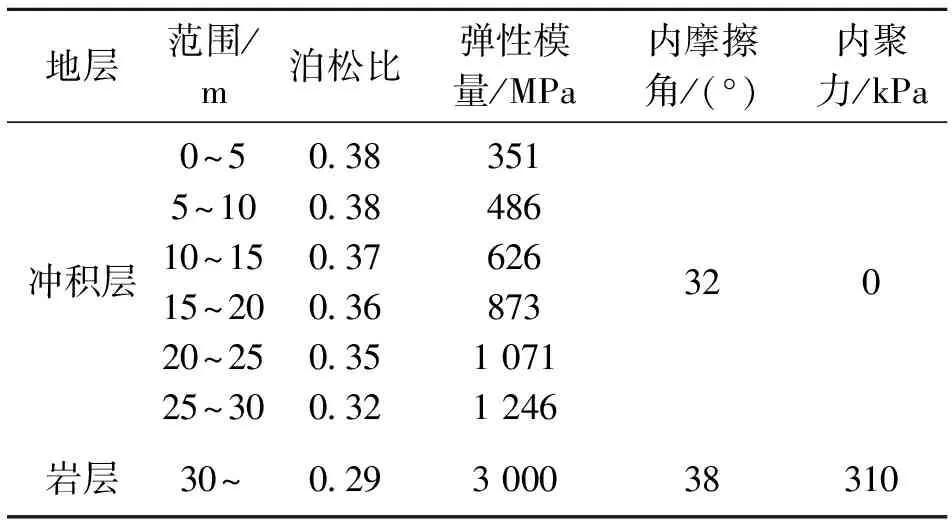
表2 坝基土岩力学参数

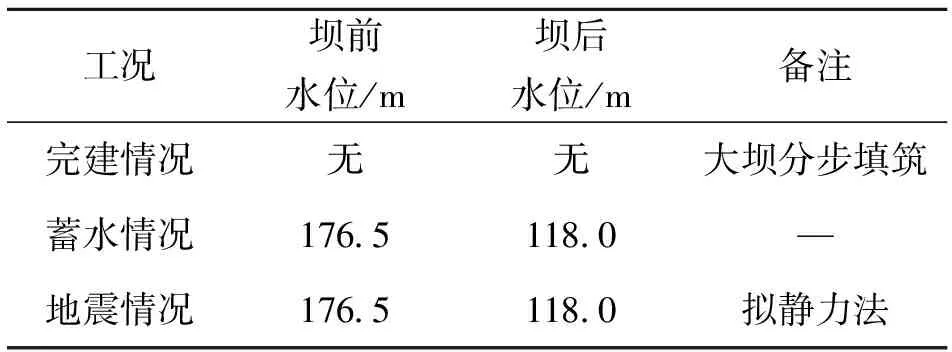
表3 计算工况

注：蓄水情况和地震情况的应力和位移均以施工完建情况为基准

4 计算结果与分析

4.1 变形

冲积层和混凝土防渗墙的模量相差大，在上游盖重作用下，防渗墙上部周边土体沉降较大，产生负摩擦效应；同时，大坝自重造成防渗墙上、下侧侧向土压力的差异，引起防渗墙向上游变位，见图3a。

蓄水和地震情况时，地下渗流场在防渗墙上游侧产生的孔隙水压力大，下游侧产生的孔隙水压力小，且上、下游孔隙水压力的差值随墙体高程增大而增大。防渗墙在孔隙水压力作用下向下游变位，并带动附近土体向下游变位，见图3b、c。

3种工况下防渗墙变形计算结果见表4，其中位移竖直向上为正，向下为负；水平位移向下游为正，向上游为负。

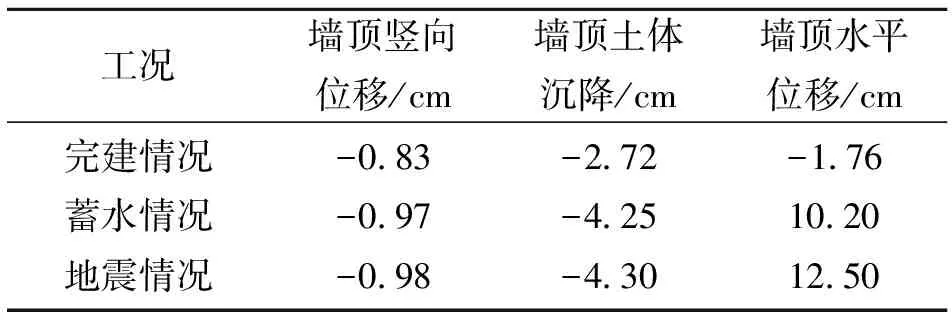
表4 防渗墙变形统计

完建情况下，防渗墙水平向上游变位，且高程越高，变位越大，墙顶向上游最大变位量为1.76 cm，见图4a；蓄水情况和地震情况下，防渗墙均向下游变位，且高程越高，变位越大，同高程地震情况的变位较蓄水情况大，墙顶向下游最大水平变位分别为10.2、12.5 cm，见图4b、4c。

将3种工况下防渗墙高程的变位点绘在同一张图上，见图4d。该图显示了各工况下防渗墙变位的相对关系。

4.2 应力

3种工况下，防渗墙上、下游侧水平应力均为压应力，且随深度增加而增加；在一定高程上，上、下游水平应力完建情况最小，地震情况最大，蓄水情况介于两者之间。3种工况下防渗墙上、下游侧应力沿深度方向分布见图5、6，防渗墙最大水平应力和最小水平应力见表5。拉应力为正，压应力为负。

表5 防渗墙应力最大值

在填筑荷载的作用下，坝体及覆盖层会产生较大的沉降，对防渗墙施加的摩擦力和侧向压力是引起防渗墙应力变形的主要原因。防渗墙长47 m，其中上部10 m位于大坝内部，因此，防渗墙的施工时机对墙体应力影响较大。本工程为了减小防渗墙的应力和变形，在大坝填筑到趾板基础高程后，坝体和冲积层基本完成了沉降变形，再施工防渗墙和趾板，所以防渗墙应力较小。

4.3 内力

采用有限元内力法，利用节点位移和节点刚度矩阵求解截面轴力、弯矩和剪力。防渗墙内力计算结果见表6，内力沿深度方向分布见图7。拉力为正，压力为负。

3种工况下，防渗墙均轴向受压，且同一高程下防渗墙轴力在蓄水情况最大，地震情况次之，施工情况最小。在完建情况，防渗墙轴力的最大值位于墙身1/3深度处，地震情况和蓄水情况下，防渗墙的轴力最大值在防渗墙中部。

完建情况的防渗墙中部以上单元受到剪力为顺时钟方向，中部以下单元受到剪力为逆时钟方向；蓄水情况和地震情况与施工情况正好相反。防渗墙剪力最大情况发生在地震情况，蓄水情况次之，完建情况最小且反向。防渗墙在深度25 m处出现剪力零点，剪力最大值发生在地震情况，为210 kN。

完建情况的防渗墙在深度5 m处产生最大弯矩，该处下游面受拉；蓄水情况和地震情况的弯矩方向与完建情况正好相反，最大值发生在深度25 m附近。防渗墙的弯矩0点位于深度11 m附近。防渗墙剪力值在地震情况最大，蓄水情况次之，完建情况最小且反向。

4.4 配筋计算

防渗墙强度的主控因素并不确定，因此，分别取最大轴力截面、最大弯矩截面和最大剪力截面每延米，按规范[3]分别进行配筋计算，配筋结果见表7。

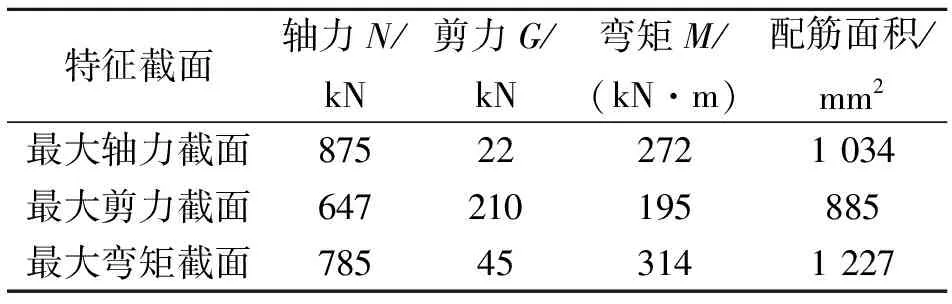
表7 配筋计算成果

表中，最大弯矩截面计算得到的配筋面积值最大，表明防渗墙的强度主要由最大弯矩控制；防渗墙每延米需配纵向受力钢筋1 227 mm2，为其防渗墙的强度设计提供了参考依据。

5 结语

深厚冲积层上的高面板堆石坝的防渗墙应力和变形特征十分复杂。运用有限元数值分析和有限元内力法，定量分析了典型特征工况下混凝土防渗墙的变形、应力和内力特性，并根据配筋计算，分析了防渗墙强度的主控因素，为防渗心墙的结构设计和强度设计提供了依据和参考，同时也表明有限元数值分析和有限元内力法是研究复杂情况下的面板堆石坝防渗墙特性的有效途径。