基于最小均方误差估计和稀疏性先验的图像去噪

孙 冬，向 豪，卢一相，饶儒婷，杨 杨

(1．安徽大学 电气工程与自动化学院，安徽 合肥 230601；2．安徽大学 电子科学与技术学院，安徽 合肥 230601)

噪声移除是图像处理领域的一个基本问题．由于人类视觉系统对图像边缘结构具有敏感性，因此对噪声污染的图像中相关边缘和纹理的精确恢复是图像去噪的主要研究内容．自20世纪60年代以来，大量的文献利用各类线性及非线性的方法对图像去噪问题进行了深入的研究和探索，采用的方法包括边缘保护去噪[1-2]、多尺度几何分析[3-6]、分形方法[7]、non-local块平均[8-10]、人工神经网络[14]和稀疏表达模型[16]等，这些算法的性能主要取决于在噪声去除的同时对图像边缘结构信息的复原能力．

近年来对图像表达模型的研究[11-13]表明，经过训练的冗余字典不仅对噪声具有较强的鲁棒性，能够产生更加稀疏的表达系数，可以灵活有效地捕捉图像的边缘结构，并且更重要的是字典的原子具有局部性、方向性和带通性的特点，这些特点与人类初级视皮层V1区的特性相符，因此相应的图像处理算法能够产生与HVS(human visual system)更加一致的结果．论文根据图像的稀疏表达模型，提出一种基于贝叶斯MMSE(minimum mean square error)估计复原框架下的图像去噪算法．

1 基于稀疏表达模型的MMSE图像复原方程

假设噪声信号的观测模型为

y=y0+e，

(1)

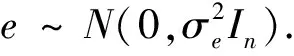
根据稀疏表达理论，若y0可被n×m维冗余字典A表达为y0=Ax0，则(1)式可写为y=Ax0+e．

通过对x0的MMSE估计，有

(2)

得到原始无噪信号y0的近似为

考虑x0的最大后验概率(maximum a posteriori, 简称MAP)估计为

(3)

记s为x的支撑，有

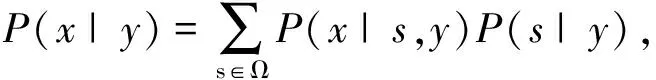
其中：Ω为x的所有可能的支撑构成的集合．对于具有某个特定支撑s*的可行解x，在进行P(x|y)求解时，求和号中只有支撑为s*的项会被保留，有

(4)

将(4)式代入(3)式得

又因为

P(xs|s,y)P(s|y)∝P(|s,xs)P(xs|s)P(s)，

有

(5)

(6)

(7)

上式也是x0的MMSE估计，即

(8)

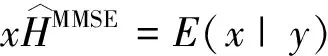
(9)

根据贝叶斯公式，(9)式可写为

(10)

上式中的P(s)项可近似为[16]

(11)

其中：α与β为参数，由x0支撑尺寸的概率密度函数P(k)决定．

对于(10)式中的P(y|s)项，由文献[15]知

(12)

其中：c1为常数．将(11)和(12)式代入(10)式，得MMSE复原方程为

(13)

2 数值求解算法

(14)

为进一步减少计算量，采用下述随机OMP算法对(14)式进行近似求解：

重复L次：

初始化阶段：k=0，初始解x0=0，初始残差r0=y-Ax0=y，初始支撑s0=support{x0}=Φ，下标集B={b1,b2,…,bm}={1,2,…,m}．

迭代阶段(重复k次)：

(1)k=k+1；

(2) 随机选择步：

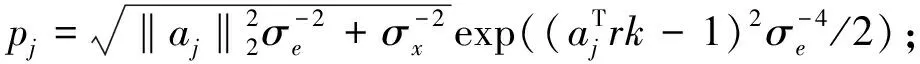
(b) 对概率pj进行归一化；

(c) 根据B中的bj所对应的概率pj，随机选择一个下标值bj0；

(3) 支撑更新步：

(a) 更新支撑sk=sk-1∪{bj0}；

(b) 更新下标集B=B/{bj0}；

(4) 更新解：计算在支撑sk下能够使‖Axk-y‖最小化的解xk；

(5) 更新残差：rk=y-Axk.

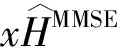
3 实 验

图1给出Lena图像在噪声标准差σe=20时的去噪结果．从帽子的边缘、眼睛的轮廓等细节可以看出，算法能够较好地对噪声污染的高频区域进行重建，主观视觉质量较高，不产生明显的锯齿和模糊现象．为进一步考查算法的去噪性能，图1给出了peppers图像在σe=50强噪声情况下的复原结果．由图1(a)、(b)可以看到，尽管图像中绝大部分的边缘细节已经几乎完全被淹没在噪声中，但该文提出的算法依然表现出了优秀的性能，提供了可接受的边缘复原结果．

图1 含噪图像(σe =50)及去噪结果((a)、(b))；含噪图像peppers去噪结果(PSNR=28.40)((c)、(d))

作为客观质量评价，图2给出了该文算法与其他3种去噪算法的PSNR结果进行对比，这3种算法分别是：Lee滤波器去噪[1]、基于平移不变contourlet变换(translation-invariant contourlet transform, 简称TICT)的去噪[10]和基于K-奇异值分解(K-singular value decomposition,简称K-SVD)算法的图像去噪[17]．

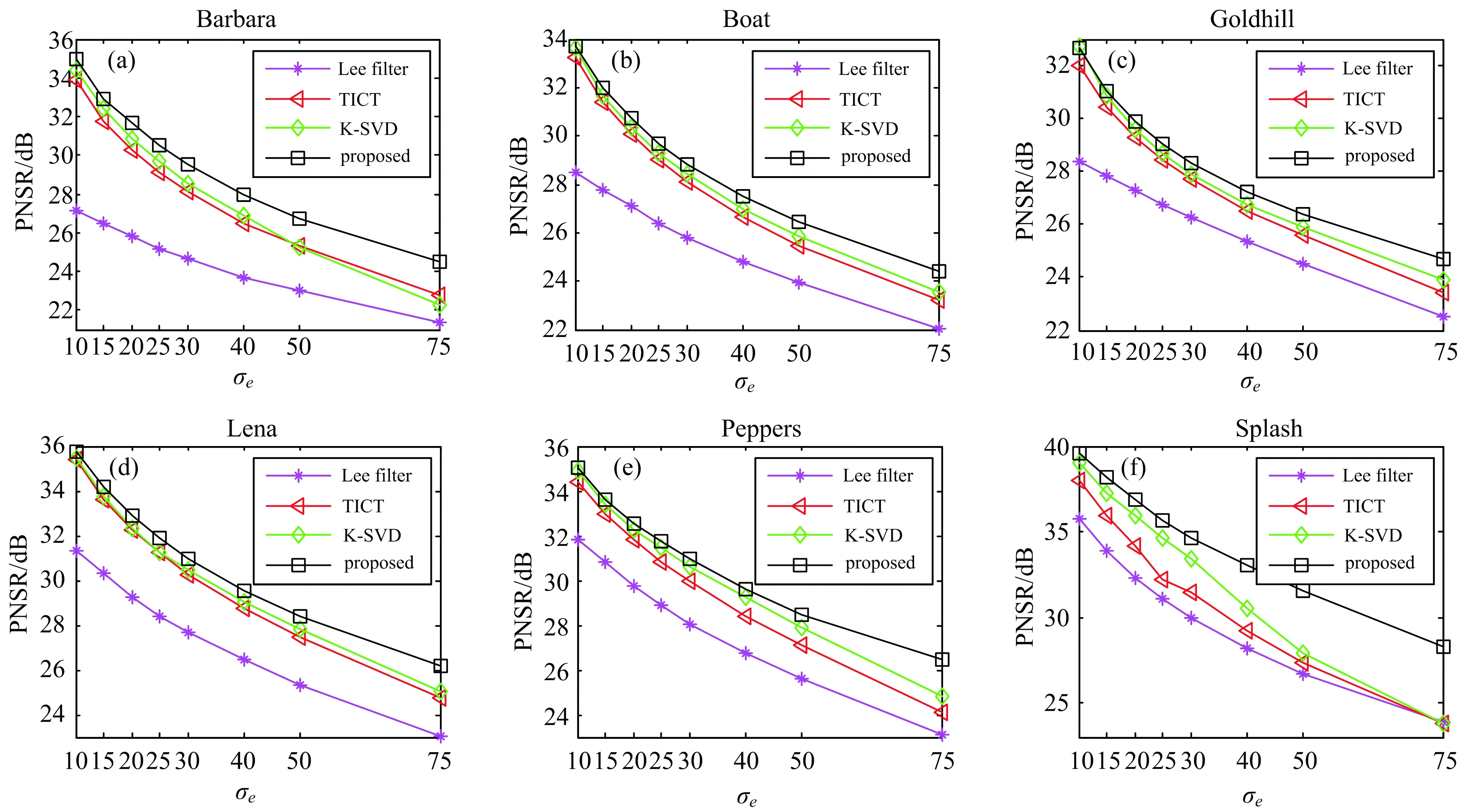
图2 PSNR数值对比

由图2可以看出，该文算法所对应的去噪图像有着更高的PSNR数值，与主观的视觉质量感受具有一致性．

4 结束语

综上所述，基于稀疏表达模型和MMSE估计的图像去噪算法能够在有效抑制噪声的同时，可以很好地保护图像的边缘结构信息，具有较高的去噪图像质量，在医学成像、测绘、视频监控等领域中拥有较大的应用潜力．下一步的研究目标应主要集中在降低去噪处理时间上，可以考虑使用图形处理器进行加速．