基于简化Bishop法的锚固路堑边坡稳定性计算

赵世乐

(湖南辉达规划勘测设计研究有限公司 长沙市 410000)

0 引言

山区公路特别是山区高等级公路地形地质较为复杂，受公路路线平面和纵面技术指标标准限制，深挖路堑较多，应进行边坡稳定性验算。对于不稳定的边坡常采用抗滑桩(预应力锚索抗滑桩)、锚杆(预应力或非预应力)框架、预应力锚索框架等锚固加强措施。当前，针对自然边坡稳定性评价的研究已趋于成熟，然而，对锚固边坡稳定性评价的介绍则相对较少。

边坡稳定性计算的方法很多，边坡破坏形态是选取计算方法首先考虑的重要因素。在公路工程中，对于规模较大的碎裂结构岩质边坡和土质边坡宜采用简化Bishop法，对可能产生直线破坏形态的边坡宜采用平面滑动面解析法，对可能产生折线破坏的边坡宜采用不平衡推力法。

针对在公路工程中大量运用的圆弧滑动面边坡稳定性计算的简化Bishop法，将锚索(杆)的锚固作用简化为作用在土条底面上的外力，推导出了锚固路堑边坡的简化Bishop法安全系数计算公式，这是对简化Bishop法的扩展，能够实现考虑锚固力作用下的边坡稳定性计算。

1 锚固路堑边坡稳定性计算

毕肖普于1955年提出一个考虑条块侧面力的稳定分析方法，称毕肖普法。但该法并没有考虑锚固力作用，无法对锚固力作用下的边坡稳定性进行计算。在基于简化Bishop法进行锚固边坡稳定性分析时，把锚固力简化为作用在土条底面上的外力，其计算简图如图1。作用在条块i上的力，除了重力Wi、土条底面的锚固力Ti外，滑动面上有切向力fi和法向力Ni。条块的侧面分别有法向力Ei、Ei+1和切向力Hi、Hi+1。

图1 锚固力作用下Bishop法条块作用力分析

若条块处于静力平衡状态，根据竖向力平衡条件，则有：

W

i

+ΔH

i

=N

i

cosα

i

+f

i

sinα

i

-T

i

sinθ

(1)

根据摩尔-库伦理论及满足安全系数为Fs时的极限平衡条件：

(2)

根据式(1)、式(2)即得：

(3)

(4)

考虑整个滑动土体的整体力矩平衡条件，各土条的作用力对圆心力矩之和为零。这时条间力Ei、Hi成对出现，大小相等，方向相反，相互抵消，对圆心不产生力矩。滑动面上的正压力Ni通过圆心，也不产生力矩。因此只有重力Wi、滑动面上的切向力fi、锚固力Ti对圆心产生力矩：

(5)

由于di=Rsinαi，且简化Bishop法假定ΔHi=0，将式(4)代入式(5)，并整理得：

(6)

其中：

式中：Fs—边坡稳定安全系数；

Wi—土条重力；

φ—土条摩擦角；

c—土条粘聚力；

li—土条底面滑动圆弧长度；

αi—土条底面滑动圆弧切向与水平向夹角；

Tj—锚固力(每延米，若该土条无锚固力则为零)；

θ—锚固力与水平向夹角。

若令锚固力Tj=0，则式(6)可简化为：

(7)

简化后式(7)即为无锚固力时简化Bishop法的计算公式。这从理论上说明了考虑锚固力时安全系数计算公式推导的正确性，这是对简化Bishop法的一个扩展，能够实现考虑锚固力作用下的边坡稳定性计算。

2 工程算例及分析

2.1 工程算例

采用文献[4]中的算例，该算例是澳大利亚计算机协会对边坡稳定性分析程序进行的一次调查中的考题，由于这次调查工作规模较大，所获得的成果比较可靠，可以作为单位或个人对自编程序考核的参考资料。其计算参数如下：

坡面水平投影长20m，垂直投影长10m，坡面线为一条直线，粘聚力3kN/m3，内摩擦角19.6°，重度20kN/m3。

文献[4]采用基于Janbu法的倾斜条块划分法计算了无锚固力作用下边坡安全系数，且与前述考题结果较吻合，并在此基础上分别采用基于Janbu法的倾斜条块划分法、理正软件、FLAC2D数值模拟计算了锚固边坡(距坡脚垂直高度为3m、4.5m和6m处加三排20kN锚固力，倾角40°)的安全系数。

按前述推导的扩展简化Bishop法安全系数计算公式，采用文献[4]中计算参数，将滑动土体划分为11块(计算简图如图2)，分别计算了无锚固力作用下、加锚作用下边坡稳定安全系数。

根据前述推导的扩展简化Bishop法，按迭代计算法，具体计算过程及结果如表1、表2：

表1 无锚固力作用下边坡安全系数计算

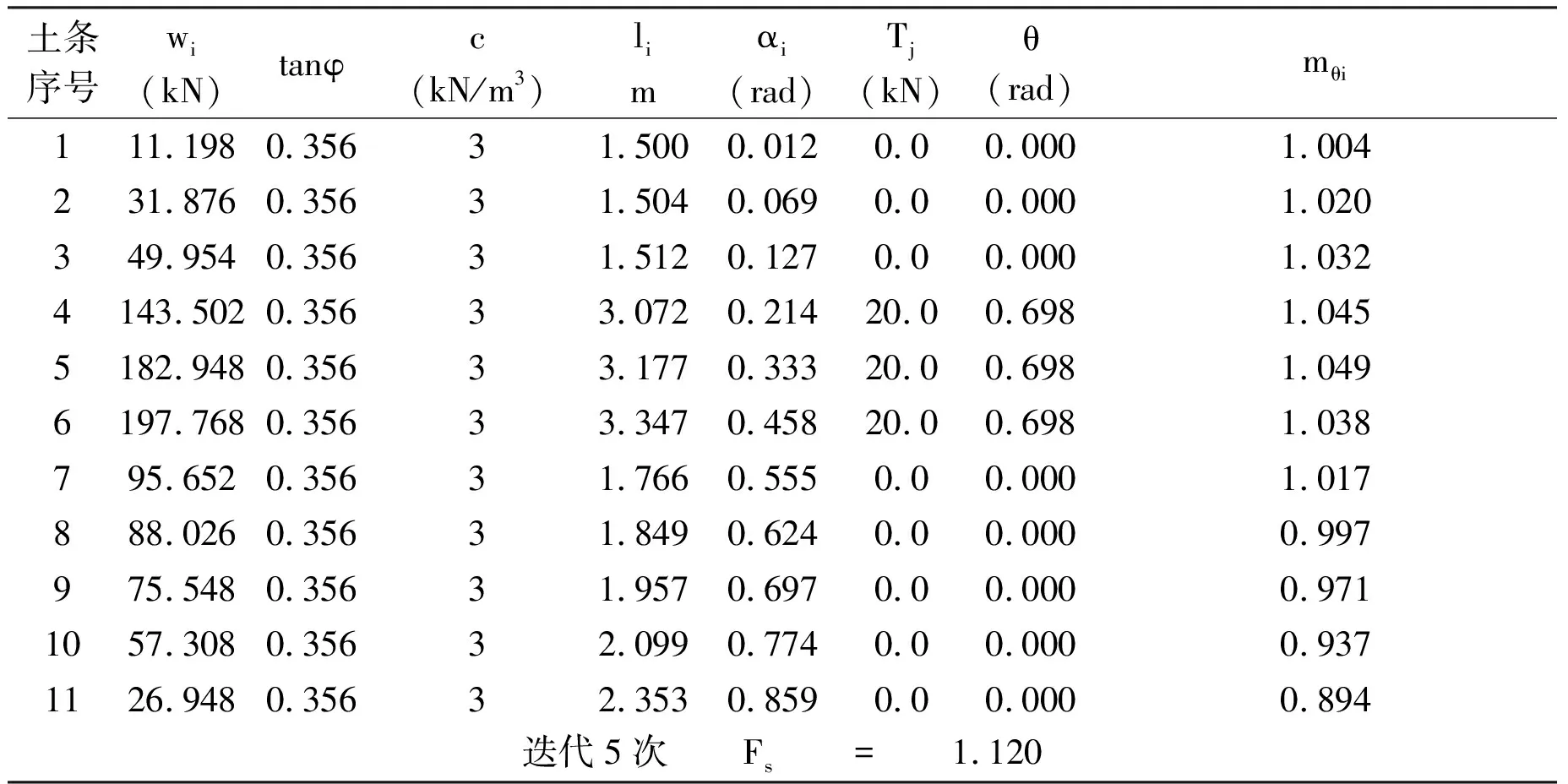
表2 锚固力作用下边坡安全系数计算

图2 边坡稳定性分析条块划分计算示意图

计算结果与文献[4]的计算结果对比如表3：

由表3可知，无锚固力作用下计算的边坡安全系数与文献[4]的三种计算结果均具有较好的吻合性，其误差均小于5%，能够满足工程要求。锚固力作用下计算的边坡安全系数与文献[4]的三种计算结果均具有较好的吻合性，特别是与Janbu倾斜条分法及FLAC2D数值计算法的计算结果，其误差均小于5%，能够满足工程要求，这也证明了按所述方法考虑锚固力作用下锚固边坡稳定性计算的可行性、合理性及正确性。

经过对比无锚固力作用下、锚固力作用下边坡的安全系数可知，无锚固力作用下自然边坡的安全系数为0.987，锚固力作用下加锚边坡安全系数为1.120，相对于自然边坡，锚固边坡的安全系数提高了约13%。锚索(杆)的加锚作用能够显著提高边坡稳定性。

2.2 计算分析

为了解锚索(杆)倾角、锚固力变化对锚固边坡稳定性的影响，维持锚固力不变，取锚索(杆)倾角为30°、35°、40°、45°、50°，或维持锚索(杆)倾角不变，取锚固力为10kN、15kN、20kN、25kN、30kN并计算其边坡安全系数。具体计算结果如表4、表5：

表4 不同锚索(杆)倾角下边坡安全系数

表5 不同锚固力下边坡安全系数

由此可见：随着锚索(杆)倾角的增加，边坡安全系数逐渐减小；随着锚固力的增加，边坡安全系数逐渐增大。因此，在锚固路堑边坡稳定不满足设计要求时，可适当减小锚杆(索)倾角或适当提高锚固力，以使边坡稳定性满足要求。

3 结论

针对在公路工程中大量运用的圆弧滑动面边坡稳定性计算的简化Bishop法，将锚索(杆)的锚固作用简化为作用在土条底面上的外力，推导出了锚固路堑边坡的简化Bishop法安全系数计算公式，这是对简化Bishop法的扩展，能够实现考虑锚固力作用下的边坡稳定性计算，并结合具体算例论述了本方法的可行性、合理性及正确性

另外，还对锚索(杆)倾角、锚固力变化对锚固边坡稳定性的影响进行了分析，并得出随着锚索(杆)倾角的增加，边坡安全系数逐渐减小；随着锚固力的增加，边坡安全系数逐渐增大。因此，在锚固路堑边坡稳定不满足设计要求时，可适当减小锚杆(索)倾角或适当提高锚固力，以使边坡稳定性满足要求，为今后类似的锚固路堑边坡稳定性计算提供了重要参考。