基于混合模型的国际原油价格预测研究

张金良，李德智，谭忠富

（1.华北电力大学 经济与管理学院，北京 102206；2.中国电力科学研究院有限公司 用电与能效研究所，北京 100192）

一、文献综述

在市场供需博弈、美元汇率、投机交易、地缘冲突、自然灾害等因素综合作用下，国际原油价格剧烈波动，增加了原油价格预测的难度。为此，构建科学合理的模型，较为准确地预测国际原油价格走势，成为学术界关注的热点和难点。

原油价格预测模型较多，归纳起来主要分为三类：时间序列模型、人工智能模型和混合预测模型。徐凌等（2013）[1]建立了自回归积分滑动平均模型对国际油价进行定量预测。包湘海等（2014）[2]通过原油价格和世界人均国内生产总值的回归模型，对国际原油价格进行了预测。熊熊等（2016）[3]将季节因子加入自回归积分滑动平均模型中，对2014—2020年的国际原油价格进行预测。尽管时间序列模型能够较好地刻画原油价格序列中的线性特征，其很难拟合原油价格序列中的非线性特征。为此，有学者将人工智能模型引入原油价格预测中。Shin等（2013）[4]利用神经网络模型预测1992年1月—2008年6月美国西德克萨斯轻质原油的月度价格。范秋枫等（2017）[5]建立模糊神经网络模型预测布伦特原油价格。Yu等（2017）[6]采用最小二乘支持向量模型预测美国西德克萨斯轻质原油价格。Zhao等（2017）[7]将深度神经网络模型应用于美国西德克萨斯轻质原油价格预测中。虽然人工智能模型能够较好地刻画原油价格序列中的非线性特征，其很难刻画原油价格序列中的线性变化趋势。由于原油价格受众多因素影响，使得其呈现出一定的周期性和非线性，单一模型不能刻画出原油价格序列的多重特性，因此，集成不同模型的混合模型将是一种有效的选择。张金良等（2013）[8]首先利用小波变换对原油价格序列进行分解，在此基础上，分别利用神经网络和广义自回归条件异方差分别对子序列进行预测。杨云飞等（2015）[9]运用经验模态分解方法将原油价格序列分解成若干个分量，在此基础上根据不同分量特征建立不同的模型进行预测。Zhang等（2015）[10]利用集合经验模态分解方法将原油价格序列分解成一系列子序列，然后分别建立最小二乘支持向量机模型和广义自回归条件异方差模型对子序列进行预测。Azevedo等（2017）[11]提出一种自回归积分滑动平均模型、指数平滑模型和动态回归的混合模型来预测美国西德克萨斯轻质原油和布伦特原油价格。Safar等（2018）[12]提出一种集成指数平滑模型、自回归积分滑动平均模型和非线性自回归神经网络的混合预测模型。现有混合预测模型较单一模型取得了较好的预测结果，但仍存在以下两点缺陷：第一，现有信号处理方法由于存在模态混叠、自适应性差等缺点，使得各分解分量的独立性不强，未能有效分离出周期性和非线性特征分量，影响了预测精度；第二，现有针对各分解分量的预测模型未能有效捕捉到原油价格序列中的周期性和非线性特征，降低了原油价格的预测精度。为此，本文首先利用变分模态分解将原油价格序列分解成一系列模态分量，变分模态分解能够克服传统分解方法中的模态混叠和自适应性差缺点；在此基础上，利用季节性差分自回归滑动平均模型预测周期性分量，其已被广泛应用于周期性时间序列的预测[13-15]；对于非线性分量则采用最小二乘支持向量机模型进行预测，其已被广泛应用与非线性时间序列的预测[16-18]。然而，最小二乘支持向量机的性能依赖于模型的参数，为此，本文利用果蝇算法对其参数进行优化，将优化后的最小二乘支持向量机用于非线性分量的预测；最后，将所有分量的预测值求和作为最终的预测结果。

二、预测模型

（一）变分模态分解

变分模态分解是由一种自适应的信号分解方法[19]。首先本征模态函数重新定义为调频-调幅信号

其中，模态分量 uk（t）可以看作一个幅值为 Ak（t）、瞬时频率为 ωk（t）的谐波信号；Ak（t）≥0；ωk（t）≥0；相位 øk（t）是一个递增函数。

假设原始原油价格序列f等于模态分量之和，则对应的约束变分模型表达如下

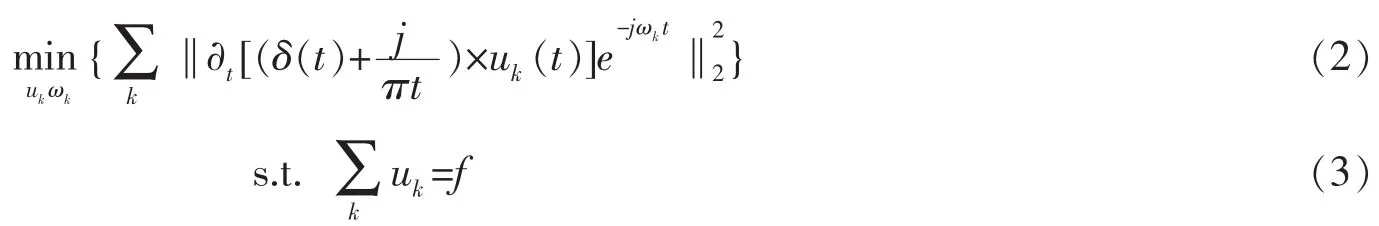
其中，uk＝{u1，u2，…，uk}为分解后的 k 个变分模态分量；ωk={ω1，ω2，…，ωk}为各模态分量的频率中心；δ（t）为狄拉克函数。

为求解式（2），将Lagrange函数引入，此时，约束性变成非约束，方程式如下

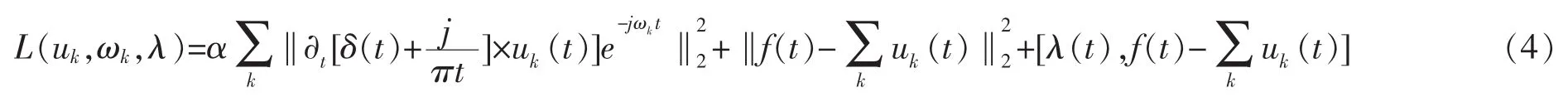
其中，α为二次惩罚因子，其值越大频宽就越小；λ（t）为拉格朗日乘法算子，利用交替方向乘子算法求约束变分模型的最优解，从而得到最终的k个模态分量。

（二）季节性差分自回归滑动平均模型

原油价格序列常常呈现出一些周期性变化规律，为此，可以采用季节性差分自回归滑动平均模型进行刻画，其表达式如下[20]

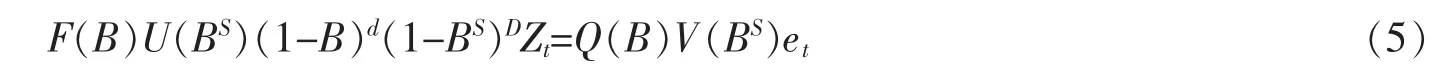
其中，F（B）＝1-χ1B-…-χpBp；Q（B）=1-σ1B-…-σqBq；U（BS）＝1-η1BS-…-ηqBks；V（BS）＝1-θ1BS-…-θoBos；p 为自回归阶数；q为移动平均阶数；d为普通差分阶数；D为周期性差分阶数；s为周期性长度；et为白噪声序列。一般来说，季节性差分自回归滑动平均模型的构建过程包括4个步骤：平稳性检验、模型识别、参数估计和诊断检验。

（三）果蝇优化的最小二乘支持向量机模型

1.最小二乘支持向量机

对于一个给定的原油价格子序列（zi，yi），i=1，2，…，l，zi∈Rn，yi∈R，利用非线性映射 φ（）将样本从输入空间映射到特征空间，其回归表达式如下[21]

根据结构风险最小化原理，回归问题可以转化为

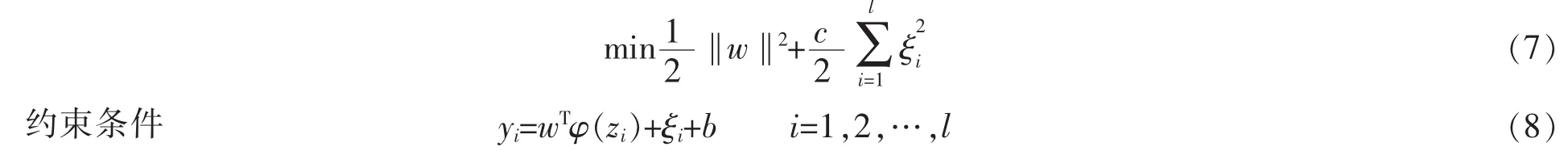
其中，w为权值系数；b为常值偏差；t为惩罚因子；ξi为松弛因子。引入拉格朗日函数，由KT条件求解，最终可得到如下的最小二乘支持向量机回归函数模型

最小二乘支持向量机常用的核函数有多种，本文选择径向基核函数，其具有较好的泛化能力[22]

此时，最小二乘支持向量机的参数选择问题即为核函数参数σ与惩罚因子c，将由果蝇优化算法给出。

2.果蝇算法

果蝇算法是一种新型的智能优化算法，其性能优于蚁群和粒子群优化算法[23]，算法步骤如下[24]：

1）设定群体初始位置（X0，Y0），种群规模M和最大迭代次数N。

2）根据初始位置，给出每个果蝇的随机方向和距离：Xi=X0+R（i），Yi=Y0+R（i）。 其中，R 为搜索步长；i为迭代次数。

4）将味道浓度判定值代入适应度函数，求出果蝇单体位置的味道浓度Smell：Smelli=Funcition（Si）

5）找出当前果蝇群体中味道浓度最高的个体：[BestSmell BestIndex]=max（Smelli）

6）记录当前最佳浓度和相应的坐标值，然后通过视觉向最佳位置飞去：Smellbest=bestSmell，X0＝X（bestIndex），Y0＝Y（bestIndex）

7）开始迭代寻优，重复步骤2）至5），判断味道浓度值是高于前者，如果是，则执行步骤6）。

（四）混合预测模型

由于原油价格受众多因素影响，使得其呈现出周期性和非线性多重复杂特性，这导致单一模型很难提高其预测精度。为此，组合周期性模型和非线性模型的混合模型将是一种提高预测精度的有效途径。然而直接利用这两种模型并不能取得较好的预期成效，为此，首先需要分离出原油价格序列中的周期性和非线性分量。本文利用变分模态分解模型将原油价格序列分解成一系列模态分量。在此基础上对每一分量进行频谱分析。若分量含有明显的周期性变化趋势，则利用季节性差分自回归滑动平均模型来预测，否则应用果蝇优化的最小二乘支持向量机模型来预测。将各模态分量预测值之和作为最终的预测结果，预测流程如图1所示，具体步骤如下：

1）利用变分模态分解方法对原油价格序列进行分解得到 u（1），u（2），…，u（k）等 k 个模态分量。

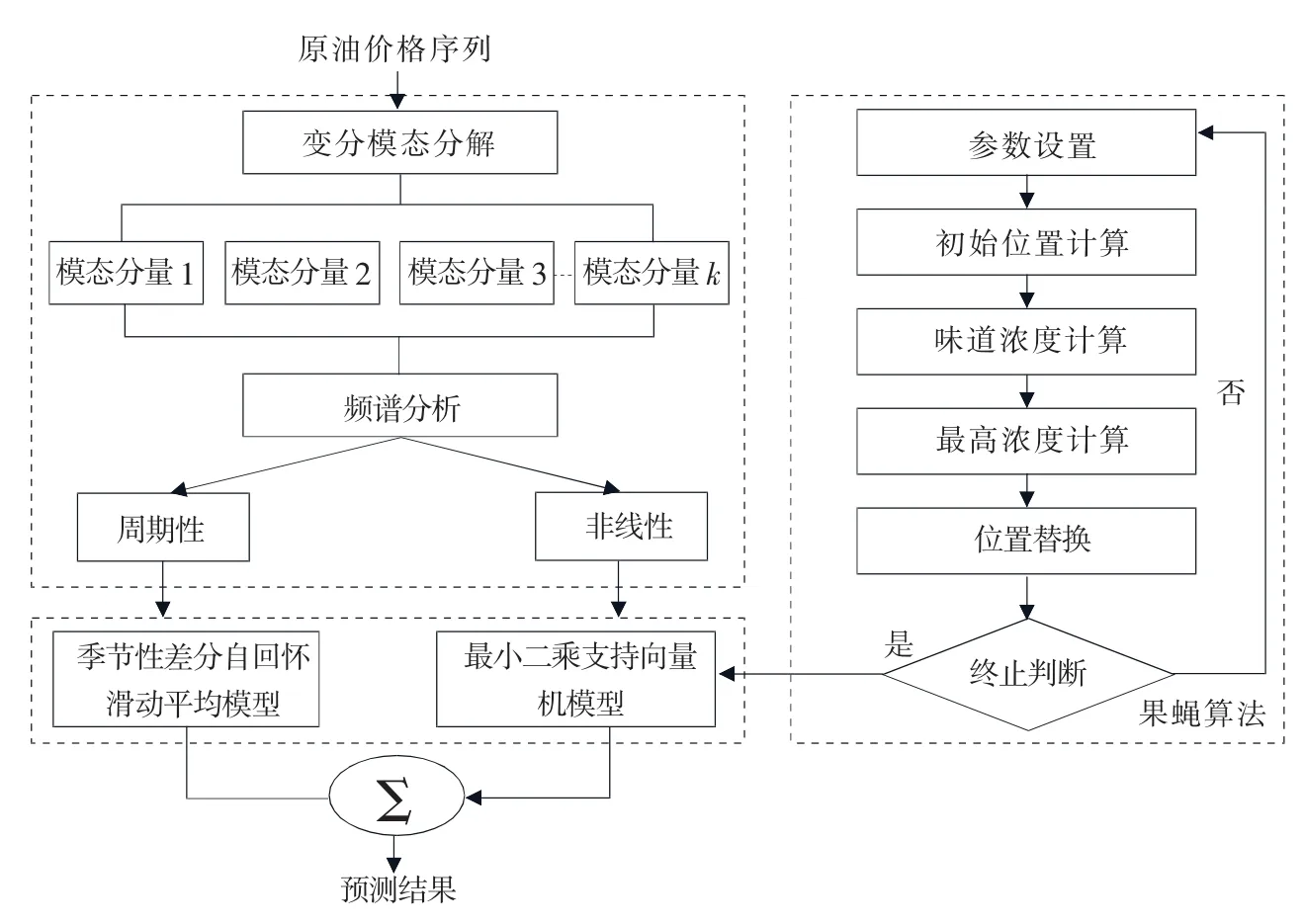
图1 混合预测模型的预测流程

2）对分解后的各分量进行频谱分析，判断哪些分量为周期性分量和非线性分量。

3）若分量具有明显的周期性趋势，则建立季节性差分自回归滑动平均模型进行预测。

4）对于剩余各分量，建立果蝇优化的最小二乘支持向量机模型进行预测。

5）将所有分量的预测值求和，作为最终的原油价格预测值。

三、算例分析

（一）预测精度的度量

为判断预测模型的实际效果，需要考察它们的预测精度。本文选择应用广泛的均方根误差（RMSE）和平均绝对百分误差（MAPE），其公式如下[25-26]

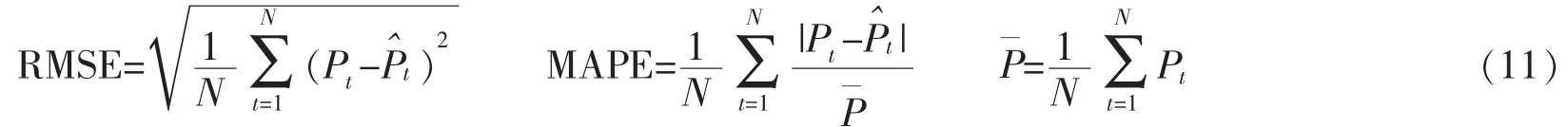
其中，Pt表示真实的原油价格；表示预测的原油价格；N是预测长度。

（二）预测精度的分析

本文选取具有代表性的美国西德克萨斯轻质原油价格作为研究对象，其数据来源于美国能源信息署官方网站。为验证本文方法的鲁棒性和精确性，这里分别对日原油价格、周原油价格和月原油价格分别进行预测。

1.日价格预测

基于上述方法，对2017年西德克萨斯轻质原油日价格进行预测分析。以2017年1月3日—2017年11月30日原油日价格作为样本数据，预测2017年12月1日—2017年12月29日的日原油价格。为检验本文模型的预测性能，分别选用变分模态分解组合季节性差分自回归滑动平均模型（即模型1）、变分模态分解组合果蝇优化的最小二乘支持向量机模型 （即模型2），季节性差分自回归滑动平均模型组合果蝇优化的最小二乘支持向量机模型（即模型3）作为对比模型进行验证。经变分模态分解后原油价格序列的各分量如图2所示。

由图2可观察到U1、U2变化呈现出一定的周期性趋势，可用季节性差分自回归滑动平均模型进行预测；而剩余各分量的非线性特性较为明显，因此，可用果蝇优化的最小二乘支持向量机模型进行预测，对比结果如表1所示。

从表1可以看出，本文提出的模型4的预测精度要高于3种对比模型。与模型1相比，平均绝对百分误差由3.39%减少至2.50%，预测精度提高了26.25%，这表明原油价格序列具有非线性特性，果蝇优化的最小二乘支持向量机模型能够较好地捕捉其变化趋势。与模型2相比，平均绝对百分误差由3.45%减少至2.50%，预测精度提高了27.54%，这表明季节性差分自回归滑动平均模型能够较好地拟合原油价格序列中的周期性变化趋势。与模型3相比，平均绝对百分误差由5.44%减少至2.50%，预测精度提高了54.04%，这表明变模态分解能够有效分离出原油价格序列中的周期性和非线性特性分量，达到分而治之的目的，从而提高了预测精度。同时，本模型的均方根误差也都小于对比模型，进一步说明了本文模型的优越性。

2.周价格预测

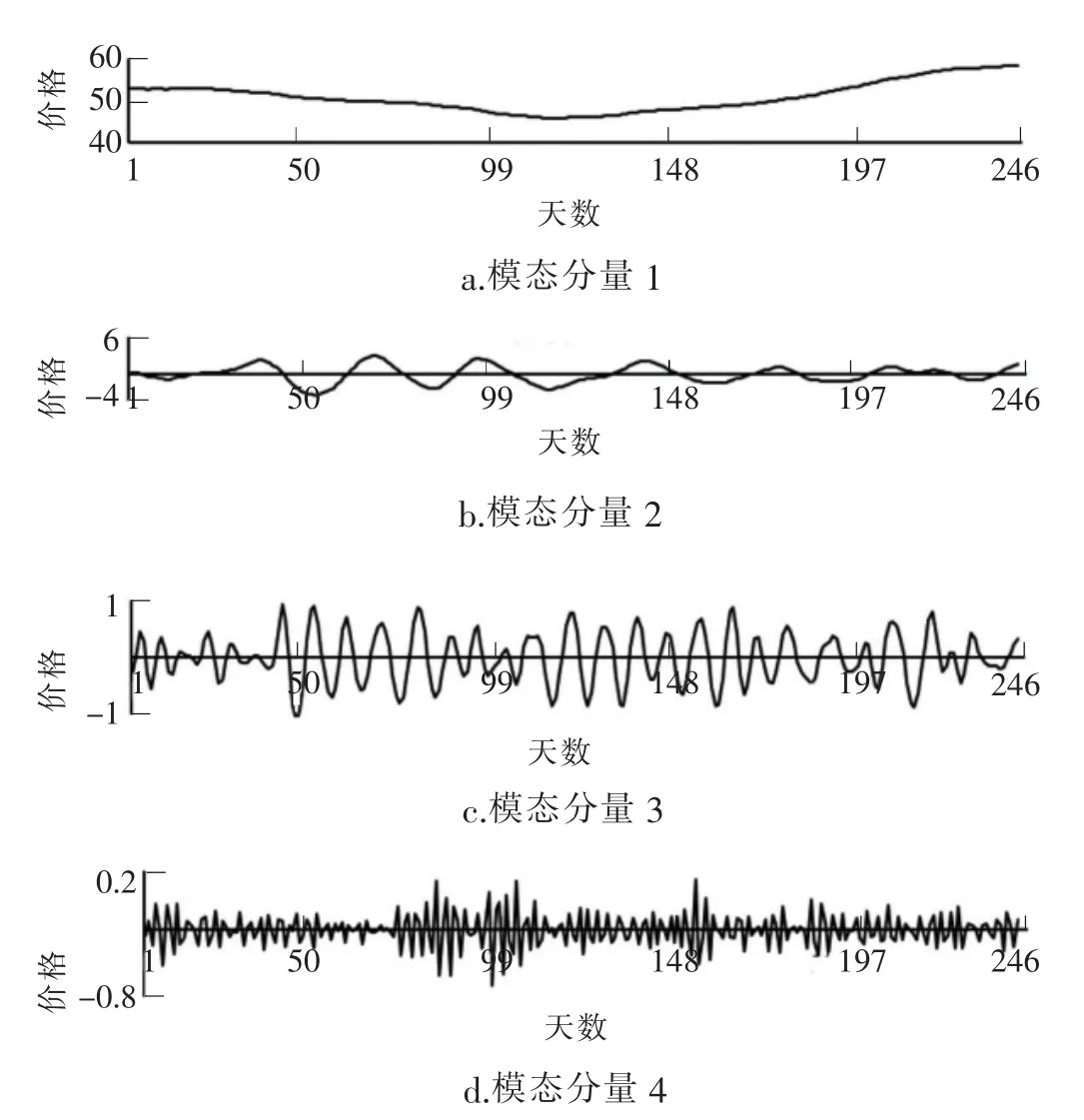
图2 原油价格序列分量

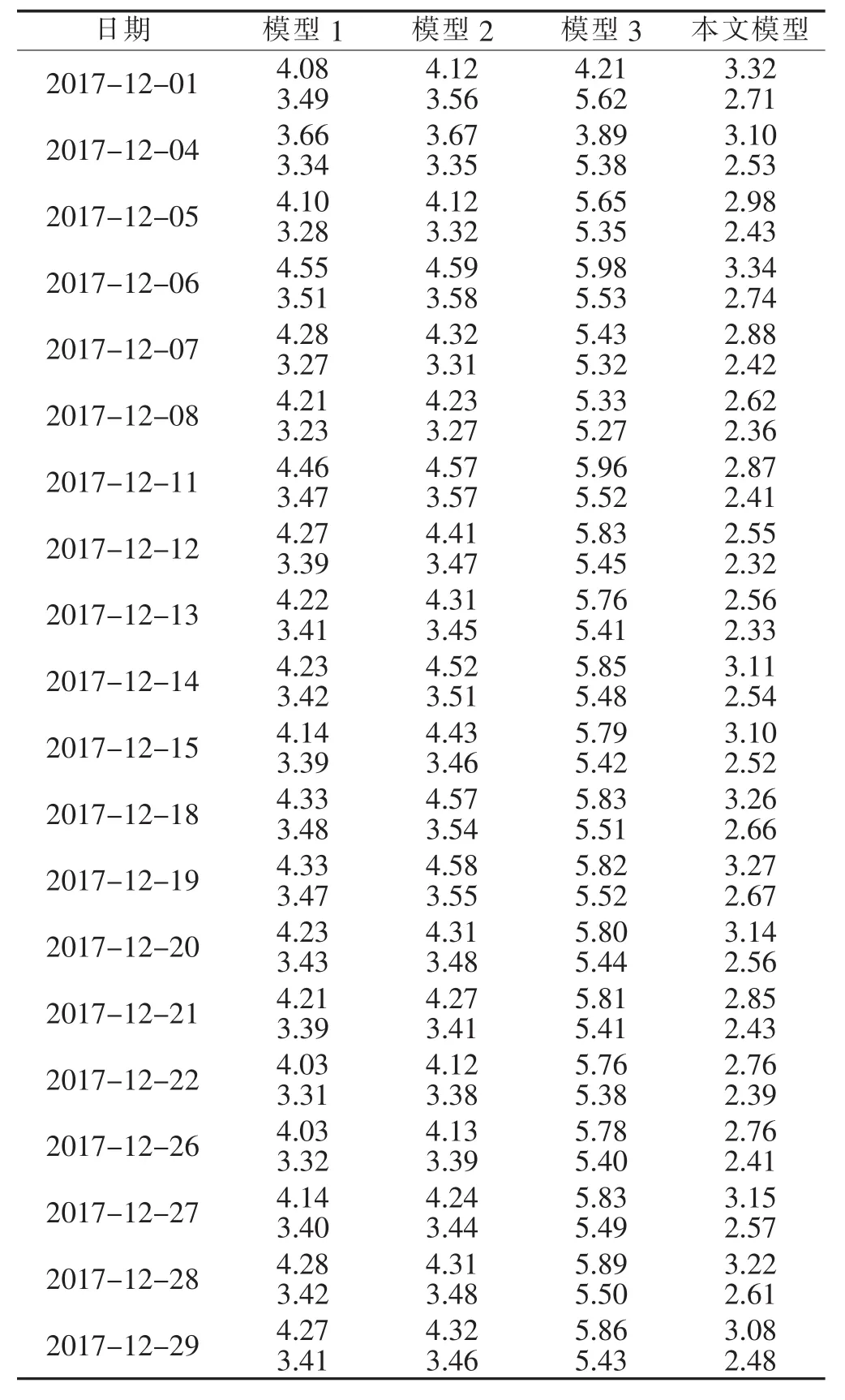
表1 不同模型RMSE和MAP的对比 %

由于原油价格预测效果受测试样本的影响，特别是样本中包括结构性断点或异常点将会导致极低的预测精度。为此，本文对西德克萨斯轻质原油周价格进行预测，这里以2000年1月7日—2008年5月30日的西德克萨斯轻质原油周价格为样本数据，预测2008年6月和7月各周的价格。历史数据表明，这两个月的原油价格是1986年以来的历史最高价格，之后国际原油油价开始暴跌，结构性断点特征明显。为验证本文所提模型的有效性，这里将其与文献[10]中的模型，集合经验模态分解+广义自回归条件异方差模型（即模型4）、集合经验模态分解+粒子群算法+最小二乘支持向量机（即模型5）、粒子群算法+最小二乘支持向量机（即模型6）进行对比，结果如表2所示。

表2 原油周价格的RMSE和MAPE %

由表2可以看出，本文提出的原油价格预测模型的平均绝对百分比误差在5%以内，可以接受，即该模型对周价格数据的预测性能也较好，特别是对原油价格序列中的异常点也有较好的预测精度。另一方面，本文提出的原油价格预测模型的性能要优于文献[10]中3种对比模型，显示了本文模型的优越性。

3.月价格预测

为进一步检验本文所提模型的预测效果，同时也为验证其泛化能力，随机选取1991年1月—2010年1月、1994年2月—2013年2月、1996年3月—2015年3月和1999年4月—2018年4月的西德克萨斯轻质原油月价格作为样本数据，以分别预测2010年2月、2013年3月、2015年4月和2018年5月的月价格。为验证本模型对原油价格的分解效果，本文分别选用小波变换+季节性差分自回归滑动平均模型+果蝇优化的最小二乘支持向量机模型（即模型7）、经验模态分解+季节性差分自回归滑动平均模型+果蝇优化的最小二乘支持向量机模型（即模型8）、集合经验模态分解+季节性差分自回归滑动平均模型+果蝇优化的最小二乘支持向量机模型（即模型9）作为对比模型进行验证。各模型的对比结果如表3所示。

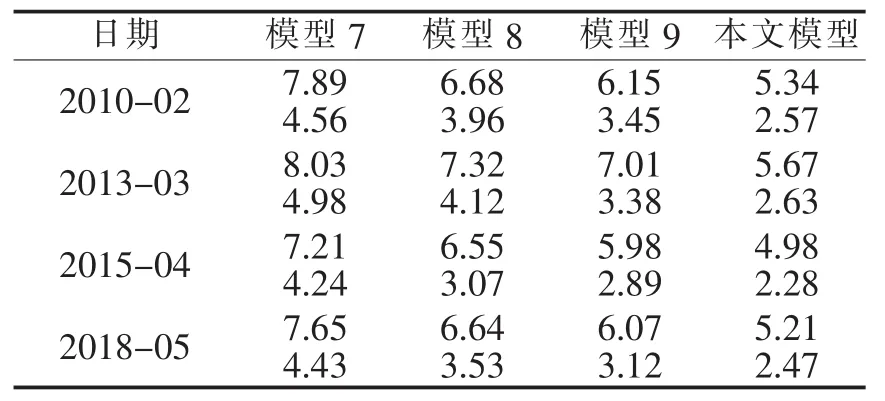
表3 不同模型RMSE和MAPE的对比 %

由表3可知，一方面，本文提出的混合模型的精度要优于对比模型，这说明本文所提模型的分解效果要好于对比模型，变分模态模型较传统信号处理方法能够更加有效地分离出原油价格序列中的不同特征分量；另一方面，本文模型对样本的选择范围不敏感，即适应能力较强，进一步证明了本文预测模型具有较好的鲁棒性。

四、主要结论

针对国际原油价格波动的复杂性，本文提出一种综合考虑原油价格周期性和非线性特征的混合预测模型，通过对西德克萨斯轻质原油日价格、周价格和月价格的测试，并与其他预测模型的对比，得出如下主要结论：第一，国际原油价格序列中的周期性和非线性分量能够被变分模态分解模型有效地分离，从而可为不同分量选择合适的预测模型。第二，季节性差分自回归滑动平均模型能够有效刻画原油价格序列中的周期性特征，而果蝇优化的最小二乘支持向量机模型能够较好地刻画原油价格序列中的非线性特性。第三，本文提出的预测模型对样本选择的随机性，样本中的结构性断点等均具有较强的适应能力，且较对比模型能够提供更为精确的预测结果，这为市场投资者预测国际油价走势，评估市场风险提供了重要借鉴，同时也为监管部门提供了重要的决策参考。