BIM技术在枢纽立交净空优化的应用研究
梁 颖 慧
(上海城建职业学院,上海 200438)
1 概述
建筑信息模型(Building Information Model,BIM)的概念由美国Autodesk公司2002年首次提出。目前已经在全球范围内得到业界的广泛认可,它可以帮助实现建筑信息的集成,从建筑的设计、施工、运行直至建筑全寿命周期的终结[1]。
净空是道路设计需考虑的关键因素,道路设计时必须满足道路最小净空要求,如各种机动车最小净空4.5 m,自行车、三轮车最小净空2.5 m[2]。现有常用的多种道路设计软件如EICAD等在立交设计方面已较成熟,虽然利用EICAD进行立交平面设计较为方便,但纵断面设计即涉及到错综复杂的上下层主线或匝道关系时仍略显欠缺。
现有二维设计中净空的考虑方法为:结合桩号对应关系,利用空间交叉的两条或多条中心线的纵断面高程结合桥梁结构厚度、横坡推算,以检查主线或不同匝道的空间交叉点是否能够满足净空要求。此方法可用于简单的双层立交检查,对于具有较近空间交叉点的三层或多层立交则变得异常复杂,效率较低。即使经过多次计算后,各交叉点虽然能够满足净空要求,但为了保证车辆行驶安全,在部分空间交叉点处通常留有一定富余,造成了资源浪费。
BIM技术中可用于检查净空的软件有多种,如Infraworks,Navisworks,Civil 3D等,但前两者更倾向于粗略测量和估计,Civil 3D可快速精确的检查且方便对净空进行优化调整。Civil 3D是一款针对多领域、一体化均适用的三维市政设计软件,由Autodesk公司在城市基础设施行业推出[3]。
2 立交净空优化原理
在Civil 3D中,数字地形模型称为“曲面”,以一块土地的三维空间模型表示,该模型由栅格或三角形组成。Civil 3D可以通过各种三维数据源如等高线、高程点等构建三维曲面,并可以对等高线、高程分布、坡度等进行分析。Civil 3D中共四种曲面:三角网曲面、栅格曲面、三角网体积曲面、栅格体积曲面,本文枢纽立交净空分析时,采用三角网体积曲面。
三角网体积曲面是从对照曲面和基准曲面中的点的组合创建的组合曲面,也称为差值曲面[4]。它能够表示出基准曲面和对照曲面之间的精确差异,从而得出精确的体积计算成果。三角网体积曲面中任何点的Z值都等于对照曲面与基准曲面在该点处Z值的差。在立交空间交叉处,可利用上层桥梁底部与下层道路或桥梁顶部先分别形成三角网曲面,进而利用两个三角网曲面形成交叉区域的三角网体积曲面,并分析三角网体积曲面的最小值,判断立交限界内能否满足最小净空要求。
3 立交净空优化方法
立交净空优化的流程见图1。
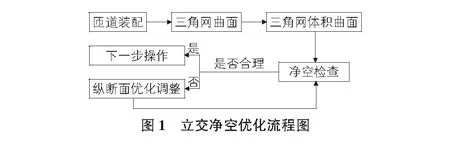
以下以立交中两条有空间交叉点的匝道SW与WN为例加以说明,其中WN匝道为上层匝道,SW匝道为下层匝道。
3.1 匝道装配
净空分析时只需分析交叉点处投影面重合的部分,故匝道装配时可根据桩号范围需要进行选择,无需在整条匝道起终点范围内进行。桥梁段匝道横断面装配、SW与WN匝道装配后的结果如图2所示。
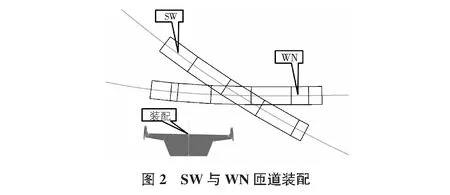
3.2 匝道三角网曲面
利用SW,WN匝道平面、纵断面、横断面装配生成道路后,提取各条匝道的三角网曲面,为三角网体积曲面的生成提供条件。另外,横断面装配设计时设置“顶部”与“底部”代码,因WN为上层匝道,SW为下层匝道,故提取WN匝道底部曲面,SW匝道顶部曲面,此两者曲面高差的大小即为净空值。提取后的匝道曲面如图3所示。

3.3 空间交叉点三角网体积曲面
SW匝道顶部与WN匝道底部三角网曲面生成后,可以利用两者生成表示各点处Z值差的体积曲面,具体操作如图4所示。曲面类型选定“三角网体积曲面”,并选取下层匝道SW的顶面作为基准曲面,上层匝道WN的底面作为对照曲面,点击“确定”即可生成。

生成后的体积曲面利用高程特性表示,如图5所示,根据图例可以看到,体积曲面最小高程为5.71 m,最大高程6.25 m,而本次设计机动车道最小净空采用5.0 m,故此节点存在优化空间。

3.4 纵断面优化调整
立交净空优化的根本在于交叉路线纵断面的优化。上述两条匝道之间最小净空为5.71 m,能够满足规范中最小净空要求,但存在富余,造成了资源浪费。在满足其他交叉点净空的前提下,可通过保持SW匝道纵断面不变,降低上层WN匝道的纵断面,使净空保持在较合理的范围区间。
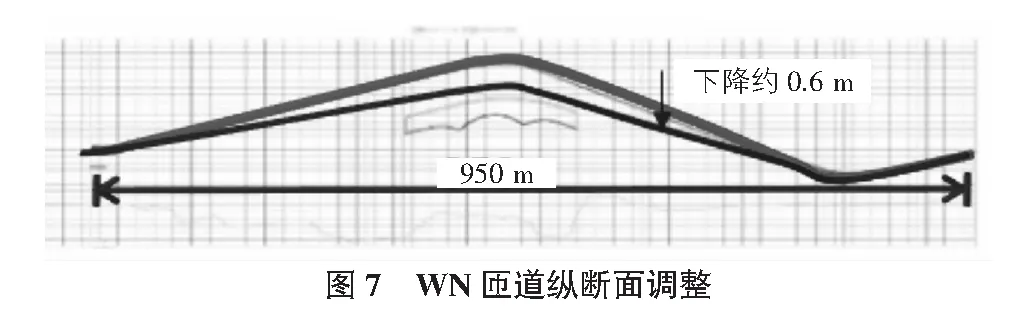
首先可用WN匝道纵断面作为基础,创建叠合纵断面,即将SW匝道纵断面投影在WN匝道纵断面上,标出交叉点的高程,如图6所示。对WN匝道纵断面进行调整,并实时查询交叉点处高程值。调整后的WN匝道纵断面高程平均下降约0.6 m,降低了匝道的整体高度,如图7所示。

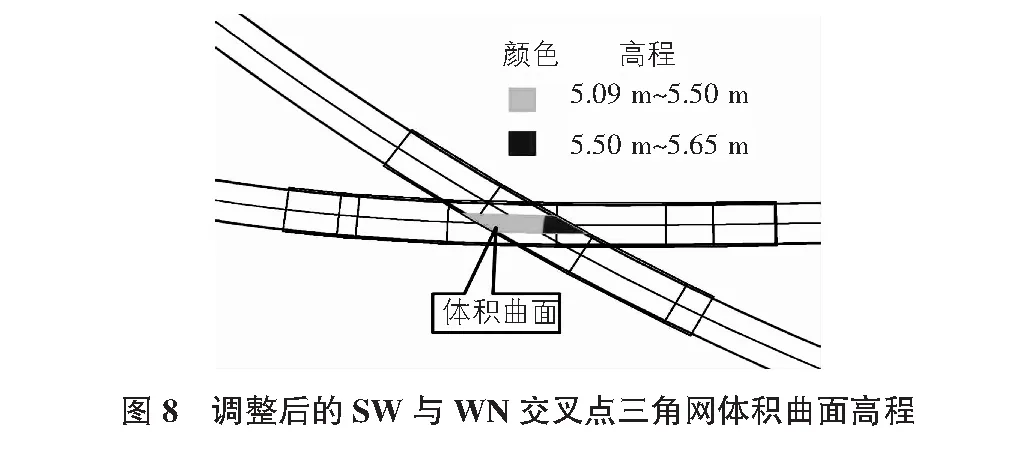
利用调整后的WN匝道纵断面,对WN匝道的三角网曲面进行更新,并与SW匝道三角网曲面重新生成交叉点处的三角网体积曲面,如图8所示。调整后的最小净空为5.09 m,符合规范要求且富余较少,节约了资源。
4 应用实例
以下通过某正在设计的枢纽立交工程北半部实例,来体现Civil 3D在净空优化设计中的应用。此立交位于某城市市区,周边环境较复杂,用地局促,设计时不仅要求平面拆迁量少,同时要求立交纵向尽量节约空间,以与周围建筑环境相匹配。为更好的体现Civil 3D在净空设计中的意义,本次设计时首先在二维条件下经过多次调整主线和匝道纵断面,得到现有二维设计条件下认为较合理的空间布置,然后利用Civil 3D进行立交净空的分析与优化。
4.1 立交净空分析
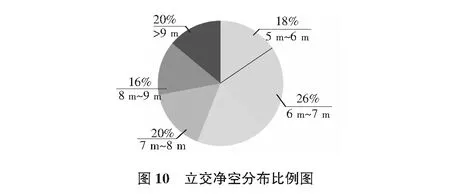
保留主线和匝道的中心线,将所有空间交叉的主线和匝道生成三角网曲面,并利用在地形投影面上有交集的三角网曲面两两生成三角网体积曲面(具体操作方法如3.3节)。 利用三角网体积曲面分析立交中所有空间交叉点的净空情况,并用不同的颜色表示不同区段的净空值,净空值分布及净空分布占比分别如图9,图10所示。

4.2 立交净空优化
由图9可以看出,立交北半部净空值为5 m~6 m比例为18%,根据本次设计对于机动车道5.0 m净空的要求,可判断此部分优化空间较大。且由图10可知,净空分布大于9 m的占比为20%,整体上分析应该存在较大的优化空间,经过对其他节点的净空值分析,可最终确定需进行调整的路线纵断面。需要注意的是,因立交匝道间上下层关系较复杂,同一条匝道可能存在下穿和上跨几条匝道的情况,故调整纵断面时应在满足规范的前提下,统筹考虑各纵断面间的关系,经过多次调整,最终达到各空间交叉点合理的净空值。
本文通过对多条匝道纵断面的调整及验证,最终得到优化后的立交净空分布如图11所示,分布比例如图12所示。
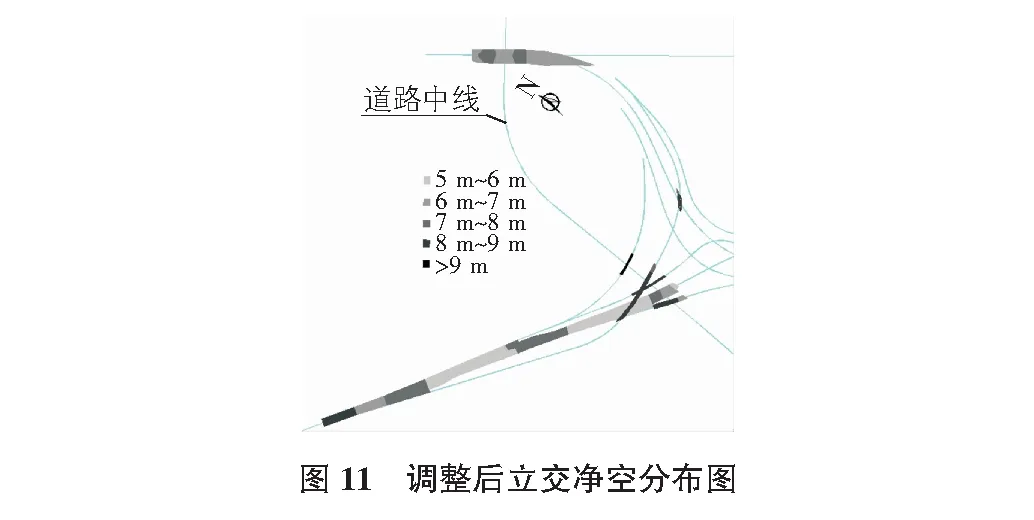

通过净空优化,立交北半部西段部分净空值平均下降约1.0 m。综合分析整个立交,第2层匝道净空值平均下降约0.5 m,第3层匝道净空值平均下降约0.8 m。调整后净空分布大于9 m的占比为14%,相对优化前下降6%。净空优化降低了立交的整体高度,使立交纵向空间设计更为紧凑且节约了工程造价。
由此可见, Civil 3D中的三角网体积曲面可反映任何立交空间交叉范围内的净空值,进而更准确的优化净空。
5 结语
现有的二维设计方法可用于枢纽立交的纵断面设计及验证,但将BIM技术尤其是Civil 3D软件应用于净空的优化,优势明显。Civil 3D用于净空优化可以节约工程造价,验证过程呈现动态变化,更直观准确。另外,BIM技术中的Civil 3D体积曲面目前多用于计算土方等工程量,将体积曲面用于立交净空检查,从而进行纵断面优化,化繁为简,具有一定的创新性与实际意义。

