层状土地基条件下具桩靴自升式钻井船插桩深度分析研究

李 晶

(交通运输部天津水运工程科学研究所 天津市水运工程测绘技术重点实验室，天津 300456)

自升式钻井船在海洋石油领域用途广泛，多用于钻井、修井，有时也被改造用于采油作业中，它一般依靠3～4根桩腿插入海底面以下一定深度，获得承载力支持[1]。在渤海的大部分油田区，沉积物来源以河流来沙为主，河流尾闾的多次摆动导致沉积物分层明显，再经波浪的分选改造后，呈现出互层且软硬不均的复杂现象[2-3]，包括迭层、软黏土与无黏性土互层、上硬下软地层关系、上软下硬地层关系等，一般层厚较小，单层厚度大多在1～5 m。软硬不均的地层特点，使得钻井船在浅层插桩时易出现承载力不足、插桩速率突变或桩底刺穿等情况[4]。为解决该问题，目前工作于中国渤海的很多钻井船都在桩端装有桩靴，大部分桩靴的最大截面宽度在6～12 m，较大的与地层接触面积降低了上部荷载的压强，能够充分利用浅部承载力，使钻井船更适合于在软土分布区插桩作业，桩基的自稳性也得到进一步增强。

新结构的应用需要相应的理论、认识、方法等的更新完善。在具桩靴钻井船的实际应用中，尚存在一些概念不明确的地方：①承载力应按浅基础计算还是按桩基础计算，在具桩靴钻井船的使用手册中，有些推荐桩基础计算公式[5]，有些推荐浅基础计算公式[6]，这反映了工程技术人员对于具桩靴钻井船作用下地基土的破坏机理认识并不明晰；②多层地基土中，当基础下一定深度范围内下卧两层或两层以上地基土时，各层土的性质对承载力的影响如何，即基础下各深度处土的强度对总承载力的贡献如何计算；③当持力层下存在软弱下卧层时，桩基础存在潜在的刺穿风险，目前的刺穿分析都是在假定软弱下卧层无限厚的基础上计算，实际常见的软弱下卧层与大尺寸桩靴的厚宽比通常很小，不满足假定条件，此时刺穿风险该如何分析。

本文基于浅基础及桩基础的极限破坏理论，以中国渤海海域的实际插桩工程案例为参考，应用有限元数值模拟手段，研究了在层状土地基条件下，具桩靴钻井船插桩时的地基土的破坏模式和插桩荷载影响深度，以及不同承载力计算公式的适用性，提出了考虑桩靴下一定深度范围内所有地层强度贡献和插桩时地层动态重分布的极限承载力计算公式，探讨了复杂地层条件下桩靴发生刺穿风险的分析方法，以期解决具桩靴钻井船应用中的工程技术疑难。

1 自升式钻井船承载力计算现状

目前，对具桩靴自升式钻井船的地基承载力及插桩深度进行评价时，常见的方法有两种，一种是以Skempton公式[7]、Terzaghi公式[8]、SNAME[9]规范等推荐的浅基础计算方法，另一种是以APIRP2A[10]等规范推荐的桩基础承载力计算方法。限于篇幅，本文不对公式进行详细介绍。

以上公式均基于均质地基土、破坏面已知、基础埋深一定等假定条件，依据静力学平衡关系建立。而自升式钻井船的桩靴基础一般为圆形或方形，地基土成层且非均质，插桩过程又是不断下插和破坏地基土的连续动态过程，很难满足公式的假定使用条件。

2 有限元数值模型建立

有限元法是一种求解偏微分方程边值问题近似解的数值技术。岩土材料有着非线性、各向异性等力学性质，大多数岩土问题非常复杂，通常难以得到准确解，而有限元法计算精度高，能适应复杂形状，在处理岩土工程问题中有着明显的优势[11-12]，一些学者利用有限元技术模拟了海洋工程插桩活动，取得了新的认识和符合实际的结果[13-15]。

本文拟采用有限元法，建立桩靴结构与海洋土体相互作用的有限元数值模型，对插桩活动进行数值模拟，通过将模拟结果与公式计算结果、插桩实例结果对比，来揭示具桩靴钻井船插桩时的地基土破坏方式，以及不同条件下的承载力计算方法。

桩靴单元为完全积分的线性实体单元，材料选用各向同性弹性材料。土体单元为完全积分的线性实体含孔隙流体单元，材料选用各向同性弹塑性材料，其中，不排水黏性土的本构模型为Mohr-Coulomb模型，排水无黏性土的本构模型为修正的Drucker-Prager/Cap模型，在帽子区域采用相关流动法则，在剪切破坏和过渡区域采用非相关流动法则。

图1 土体及桩靴的有限元网格Fig.1 FEM Meshes of spudcan and soil

本文采用的桩靴整体类似于陀螺形，下部呈锥体，最大截面直径为9.14 m。土体范围总宽度为100 m，土体深度为40 m。桩靴周边的网格单元尺寸为0.5 m，向远处逐渐增大至5 m，以节省计算成本。整个模型共有节点738个，单元683个，如图1所示。

桩土之间的接触关系为具有主从关系的面对面接触，以桩的接触面作为主面，土体接触面作为从面，采用罚函数算法，垂向接触属性为“硬”接触，切向接触可有限滑移，滑移摩擦由Coulomb接触法则控制。

整体模型受到的外部荷载主要为重力和静水压力，初始条件主要有重力、孔隙比和孔隙水压力的分布，边界条件包括侧边界的水平位移约束、底边界的垂直位移约束、桩靴体的初始平动和转动约束。为了控制整体模型在桩靴贯入之前不发生较大变形，首先设定地应力平衡分析步，在考虑桩土质量、形状尺寸和整体受力情况下，使土体均匀沉降，达到地应力平衡状态。

桩靴的贯入采用位移贯入法，在土壤力学分析步中，通过指定桩靴体的竖向位移—时间函数来实现。在该步骤中，网格单元会发生大的变形，因此，除了合理设置网格大小与插桩深度的尺寸比例以外，还利用了有限元模型本身的几何非线性分析功能，以适应大变形计算。同时，由于插桩过程是荷载的快速加载过程，孔隙水压力来不及消散，因此，采用瞬态孔隙水压响应方式。

3 有限元数值结果分析

为研究层状土复杂地基条件下桩靴底部承载力分布的规律，分别选取上硬下软地层、上软下硬地层两种情况进行模拟研究。

3.1 上硬下软地层中地基土破坏形式

设置上覆5 m厚的φ=22°砂土硬层，下伏c=15 kPa的黏性土软层作为地层模型，对桩靴贯入10 m深度地层的插桩现象进行了有限元仿真模拟。模拟结果显示，地基土的破坏形式在4.3 m以浅深度类似于整体剪切破坏，随后转为类似冲剪破坏，整体剪切破坏区的底界面并不是破坏形成的曲面，而是软硬土层的交界面。当在上部硬层插桩时，由于上层土的变形模量大于下层土，因此，上层土中的应力扩散现象明显(图2)，下部软层受应力扩散影响，塑性应变区范围呈一定倍数放大(图3)。这说明在上硬下软地层中插桩时，桩周受扰动土体的范围比较大，同时，下部软层虽不与桩靴直接接触，但发生了大范围的塑性变形，无疑会影响到层状土地层整体承载力的发挥。

图2 上硬下软地层中的剪切应力区分布Fig.2 Distribution of shearstress (S12) in upper-hard-lower-soft layers图3 上硬下软地层中的等效塑性应变区分布Fig.3 Distribution of equivalent plastic strain (PEEQ) in upper-hard-lower-soft layers

图4 上软下硬地层中的剪切应力区分布Fig.4 Distribution of shearstress (S12) in upper-soft-lower-hard layers图5 上软下硬地层中的等效塑性应变区分布Fig.5 Distribution of equivalent plastic strain (PEEQ) in upper-soft-lower-hard layers

3.2 上软下硬地层中地基土破坏形式

设置上覆5 m厚的c=15 kPa黏性土软层，下伏φ=22°的砂土硬层作为地层模型，对桩靴贯入10 m深度地层的插桩现象进行了有限元仿真模拟。模拟结果显示，地基土的破坏形式类似于冲剪破坏，当在上部软土层中插桩时，由于上层土的变形模量小于下层土，因此，上层土中的应力扩散现象不明显，主要在桩靴侧下方形成了尺寸略大于桩靴的应力泡(图4)，上部软土被挤向桩靴四周，难以在下方硬层生成等效塑性应变区(图5)。

3.3 上硬下软地层中的承载力分布

在上硬下软层状土中插桩时，随着插桩深度的增大，桩靴底部一定厚度的硬土层会被压入到软土层中，有学者称其为“砂土塞”[16]。本文有限元模拟结果也发现了这种现象，通过跟踪“砂土塞”的动态变化发现，其本质是原始地层结构在插桩过程中发生了重分布，部分硬土随桩靴压入到了下部软层，厚度随插桩深度的增大而减小，部分硬土涂抹在了井壁。可见，插桩过程中原始地层结构的重分布是个动态变化的过程，图6反映了桩靴底部有一定厚度的硬土被压入软土中且变得密实。通过多次拟合分析发现，桩靴下部硬土层的动态厚度与插桩深度呈如下关系

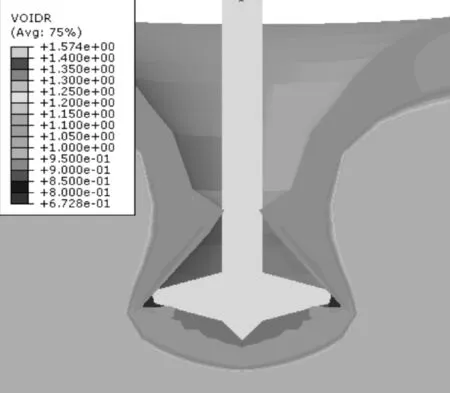
图6 “砂土塞”模拟过程示意图Fig.6 Schematic diagram of “sand plug” simulation process

(1)

式中：Hst为桩靴下端硬土层的实时厚度；Hs为硬土层的原始厚度；α为系数，与桩靴尺寸、上下地层强度比等因素有关，在本文有限元模型中约为0.15；Dt为实际插桩深度。

基于以上认识，本文提出一种计算具桩靴钻井船插桩承载力的新思路，既考虑了插桩影响深度范围内所有地层对总承载力的贡献，又考虑了插桩引起的地层动态重分布现象。具体实现方法为：当插桩至某深度时，将桩靴下部3.0B深度内的地层均作为地基持力层看待，首先将其离散成厚度很小的微元地层，并根据各微元地层距桩靴底面的距离，赋以不同的权重系数；然后利用均质土中承载力计算公式计算出每个微元地层的承载力；最后将各微元地层的承载力乘以相应的权重系数，并进行累加，即得到插桩至该深度时的地基极限承载力。可用公式表达为

(2)

式中：Pu,t为插桩至某一深度时桩靴底部地基的极限承载力；Pui,t为插桩至某一深度时各微元地层的极限承载力，可用均质土中承载力计算公式计算得出；ki为各微元地层极限承载力占总极限承载力的权重系数。

以有限元模型中假设的上硬下软地层参数为例，令各微元地层的厚度均为0.1 m，参考《建筑地基基础设计规范》[17]中附加压力系数随深度的减小以及软弱下卧层中的应力扩散现象，各深度处的相对权重分别设为：0～B/2范围，1.0；B/2～1.0B范围，0.8；1.0B～1.5B范围，0.6；1.5B～2.0B范围，0.4；2.0B～2.5B范围，0.2；2.5B～3.0B范围，0.1。

图7 上硬下软地层土中有限元 模拟与公式计算结果对比(上层φ=22°，下层c=15 kPa)Fig.7 Comparison between finite element simulation and formula calculations in upper-hard-lower-soft layers

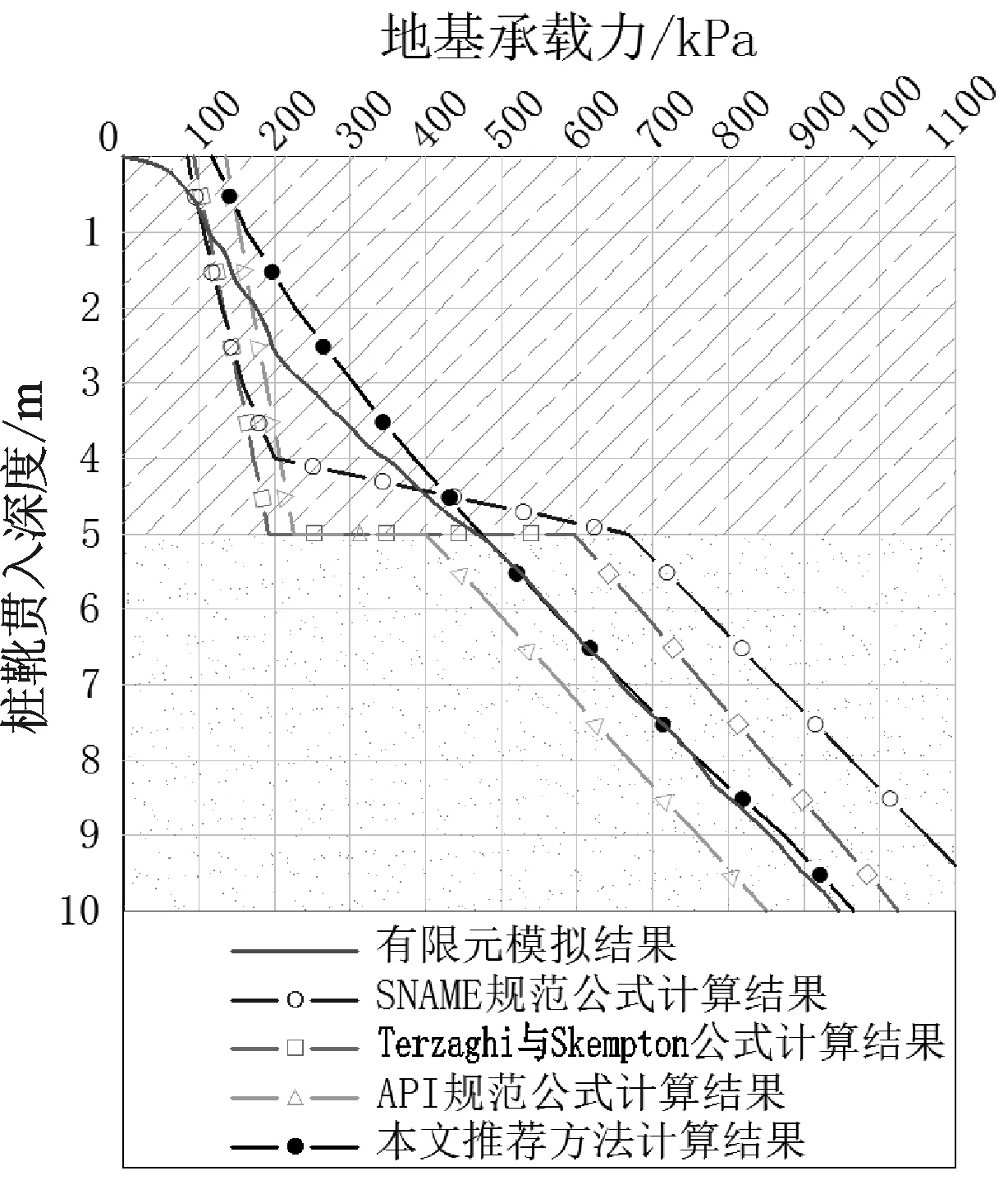
图8 上软下硬地层土中有限元 模拟与公式计算结果对比(上层c=15 kPa，下层φ=22°)Fig.8 Comparison between finite element simulation and formula calculation in upper-soft-lower-hard layers

本文基于Skempton公式和Terzaghi公式，分别计算出黏性土和砂土微元地层的承载力，然后应用公式(2)计算出总承载力。图7给出了有限元模拟地基承载力曲线及各公式计算结果，模拟曲线形态近似于a<1的幂函数，与均质黏土中的曲线形态很相似，表明较厚的下伏软黏土对总承载力的影响较大。比较公式计算结果和数值模拟结果，Terzaghi与Skempton公式组合、APIRP2A规范公式的计算结果在砂土硬层中偏大，而在黏土软层中偏小，这是由于在上层砂土中，公式未能考虑桩靴尺寸过大导致的下伏软黏土受压变形、及其对承载力的削弱影响，而在下层黏土中，公式无法体现插桩引起的部分砂土跟随贯入导致的地层重分布现象。SNAME公式的计算结果总体偏小，是因为它没有考虑到上覆砂土层的强度性质，只给出了下限解。采用本文推荐的公式(2)推得到的计算结果与数值模拟结果吻合很好。

3.4 上软下硬地层中的承载力分布

在上软下硬地层中插桩时，未出现地层结构动态重分布现象，而且由于应力扩散现象不明显，因此，在采用公式(2)计算的总承载力时，赋予下部地层的相对权重不宜过大。

图8给出了有限元模拟的承载力曲线及各公式计算结果，模拟曲线在上部黏土中微凹，在下部砂土近似于直线分布。SNAME规范公式、Terzaghi与Skempton公式组合的计算结果都在黏土中偏小而在砂土中偏大，SNAME规范虽能体现桩靴在上部软层中当距下伏硬层较近时出现的承载力增大现象，但在砂土中的计算结果明显偏大。API RP2A规范公式的计算结果整体偏小。本文推荐的公式(2)得到的结果在黏土中略大，在砂土中与模拟结果基本一致。

4 工程实例计算

某井场位于中国渤海曹妃甸区块，受古滦河三角洲沉积作用控制，地层软硬互层现象显著。工程地质勘察在40 m深度内揭示有15个地层，各层岩土定名及主要地层参数见表1。

表1 渤海曹妃甸区块某井场地层参数Tab.1 Stratigraphic parameters of a well site in Caofeidian

根据表1中的地层参数建立有限元模型，对桩靴贯入10 m深度的插桩现象进行了仿真模拟。结果显示，井场地层中存在上硬下软地层关系，在插桩过程中符合本文所揭示的地层动态重分布原则，且下部相对较软的黏土层因受压而变薄；从Mises应力的分布来看(图9)，应力在桩靴以下1B内的地层间传递与扩散较为连续，随着深度的增大，应力扩散变得不连续并逐渐衰减；当插桩至上部硬层时，桩靴能否发生刺穿可用软弱下卧层中的塑性应变是否超过了地层的塑性应变极限来衡量(图10)，但当软弱下卧层厚度过小时，进行刺穿分析实际意义不大，因为即便发生了刺穿也表现为桩靴竖向位移的微小调整。

图9 某井场插桩时的Mises应力分布Fig.9 Mises stress distribution of pile insertion in the well site图10 某井场插桩时的等效塑形应变区分布Fig.10 Equivalent plastic strain (PEEQ) distribution of pile insertion in the well site

实际在该井场就位的钻井船为“胜利六号”，桩靴宽9.14 m，高1.5 m，最大截面底面积72.25 m2，单桩极大荷载21 337 kN，实际插桩深度为2.5 m。图11给出了有限元模拟地基承载力曲线、公式计算结果及实际插桩荷载及深度。有限元数值模拟的插桩深度约1.9 m，与实际插桩深度仅差0.6 m，可见，有限元数值模拟结果具有一定的准确性。

采用SNAME规范公式预测的插桩深度为1.2 m。SNAME规范虽然考虑了上软下硬地层中的挤压破坏影响和上硬下软地层中的刺穿破坏影响，但在较厚层的砂土中计算结果整体偏大。

图11 某井场有限元模拟、公式 计算及实际插桩结果对比Fig.11 Comparison of FEM simulation results, formula calculation results and actual pile insertion results of the well site

采用Terzaghi与Skempton公式组合预测的插桩深度为1.5 m。在非均质土中，Terzaghi公式的计算结果偏大，但曲线走势与数值模拟结果较为接近，如采用一定的安全系数予以修正，也能得出较为满意的预测效果；Skempton公式的计算结果整体偏小，更适合用于计算表层厚层黏土的承载力。

采用API RP2A规范公式预测的插桩深度为4.0 m。API RP2A规范公式的计算结果整体偏小，预测结果偏于保守。

采用本文推荐方法计算得出的结果与数值模拟结果非常接近，预测的插桩深度也为1.9 m，可见，将本文推荐方法用于计算复杂层状土中的插桩承载力，具有较好的适用性，而且，在实际应用中，该方法远较建立有限元数值仿真模型简便快捷。

5 小结与展望

通过有限元数值方法，模拟了具桩靴自升式钻井船贯入层状土复杂地基中一定深度的动态过程，取得了地基土破坏形式、插桩荷载影响深度、地基承载力计算方法等多方面认识。

(1)在上硬下软的层状地层中插桩时，随着插桩深度的增大，地基土的破坏形式由类似整体剪切破坏转为冲剪破坏，整体剪切破坏时底界面是软硬土层的交界面。当插桩在上部硬层时，下部软层受应力扩散影响，塑性应变区范围呈一定倍数放大，随着插桩深度的增大，桩靴底部有一定厚度的硬土层被压入到软土层中，使地层结构发生了动态重分布。

(2)在上软下硬的层状地层中插桩时，地基土的破坏形式类似于冲剪破坏，当插桩在上部软土层中时，下部硬层受应力扩散影响的程度较小，上部软土主要被挤向桩靴四周，不会出现地层动态重分布现象。

(3)在实际工程中，地基土多为复杂的层状土，其层厚远小于桩靴的宽度，采用现有公式计算其承载力时，都具有各自的局限性。其中，SNAME规范公式虽能够反映出软硬交互地层中的挤压或刺穿破坏特点，但在砂土层中的计算结果过大；API RP2A规范公式属于桩基础公式，计算结果总体偏小；Terzaghi公式的计算结果在砂土中偏大，采用一定的安全系数修正后，可以用于预测插桩深度；Skempton公式单独用于计算层状地层中的黏土层承载力时，结果偏小。

(4)通过分析有限元模拟插桩过程中的应力应变分布规律，本文提出了一种插桩承载力计算的推荐方法，既考虑了桩靴下部3.0B深度内所有微元地层对总承载力的贡献，又考虑了在上硬下软地层中插桩时的地层动态重分布现象，通过采用Terzaghi公式与Skempton公式计算各微元地层的承载力，再乘以各微元地层权重系数，最后求得的总承载力，无论在上硬下软、上软下硬地层结构中，还是在复杂的实际层状地层中，其结果都和有限元数值模拟结果非常接近，其预测的插桩深度也和实际插桩深度较为接近，可以作为精确计算插桩承载力的一种方法使用。

(5)本文建立的有限元数值模型，在分析评价地基土的破坏形式、插桩荷载影响深度、承载力计算公式的适宜性等方面，取得了较好的应用，但未考虑到上部土体回淤对承载力的影响，也未给出桩靴发生刺穿风险的具体判别方法，在日后的研究中，还有待进一步完善与提升。