基于Budyko方程的小理河流域径流响应研究

巩 瑶,莫淑红, 李子龙, 沈 冰

(1. 西安理工大学 省部共建西北旱区生态水利国家重点实验室，陕西西安710048；2.三门峡市水利勘测设计有限责任公司，河南三门峡472000)

河川径流的变化作为全球变化的重要组成部分，其相关研究备受瞩目，由于气候条件的不断变化和人类社会的加速发展，河川径流在两者的综合作用下响应显著，这也导致区域水资源时空分布发生变化[1-3]。环境变化通常包括流域内人类活动和气候变化两部分，由于流域气候、人类活动对水文过程的综合影响，不同流域在不同年代的水文响应并不相同[4-6]，为此，定量区分气候变化和人类活动对径流变化的影响程度是非常必要的。统计和图形分析法、气候敏感性分析法和水文模型法是定量区分两大影响因子对径流量变化的影响程度的主要方法，但上述方法对水文气象及人类活动数据资料要求较高[7]。近年来，以Budyko 水热耦合平衡理论为基础的水量平衡方法也被广泛用于量化分析气候变化和人类活动对径流变化的影响[8-11]，相较于其他方法，该方法可直接单独估算出气候变化或人类活动对径流变化的贡献程度[12-13]。

小理河流域地处我国西北黄土高原地区，是生态环境脆弱带以及气候变化的敏感区域。20世纪70年代以来，伴随着国家一系列政策法规的出台实施，该地区生态治理、水利工程建设等人类活动不断加强，由于土地利用方式的改变，加之大量水土保持工程的建设，改变了流域下垫面条件，从而影响了流域水文循环和水资源形成过程[14]。因此，探究变化环境下小理河流域的水文响应特征，厘清气候变化和人类活动对径流变化的分项贡献，对指导该区域水资源规划和管理具有重要意义。本文基于Budyko方程对降水量、潜在蒸散发量、径流量关系的描述，定量计算研究区气候变化和人类活动对其径流变化的贡献，从而探讨该方法在黄土高原地区的适用性。

1 研究区概况及数据来源

小理河发源于陕西省横山县，是大理河的主要支流之一，位于东经109°16′～109°51′、北纬37°36′～37°49′之间。小理河全长63.7 km，总流域面积约为820.8 km2。小理河流域属黄土丘陵沟壑区，地形地貌特征为梁峁起伏，夏季气候炎热且降雨较多，冬季寒冷干燥且降雨较少。全流域以草地、耕地和林地为主要植被，大约占全流域的96.91%，流域土壤类型主要为黄土和风沙土，其面积分别占总面积的96.07%和2.32%[15]。

小理河流域出口断面控制站为李家河水文站，本研究收集了李家河水文站的径流资料；同时，收集了流域内艾好峁、大路峁台、高镇、李家坬、李孝河和李家河6个雨量站的降水资料，并基于ArcGIS平台利用泰森多边形法，将各雨量站资料加权平均作为流域降水量的基础数据。年潜在蒸散发量采用世界粮农组织(FAO)推荐的Penman-Monteith方法计算获得。气象资料来自于中国气象局的中国气象数据共享服务平台，收集整理了距离研究区最近的横山气象站的日照时数、平均最低气温、平均最高气温、平均本站气压、平均气温、平均风速、平均水汽压和平均相对湿度8个气象因子的资料，上述水文气象资料时间序列均为1978—2010年。小理河流域水文气象站点分布如图1所示。

图1 小理河流域水文气象站点分布Fig.1 Hydrological stations in Xiaolihe basin

2 研究方法

前苏联气候学家Budyko在进行全球水量和能量平衡分析时发现，地面长期平均蒸散发量主要由大气对地面的水分供给(降水量)和能量供给(净辐射量或潜在蒸散发量)之间的平衡决定。在多年尺度上，用降水量P代表陆面蒸散发的水分供应条件，用潜在蒸散发量EP代表蒸散发的能量供应条

件，对于量EP/P<1的流域，能量是其蒸散发量的制约条件，而对于EP/P>1的流域，供水条件是其蒸散发量的限制条件，其水热耦合定量关系可用Budyko方程简单表达为E/P=f(EP/P)=f(φ)[16]，其中φ为辐射干旱指数(简称干旱指数) ，E为流域蒸发能力。对于此方程，国内外学者们经过大量的分析，提出了如表1所示的不同形式的表达式，其中n、ω、w和ε是表征下垫面特征的参数。

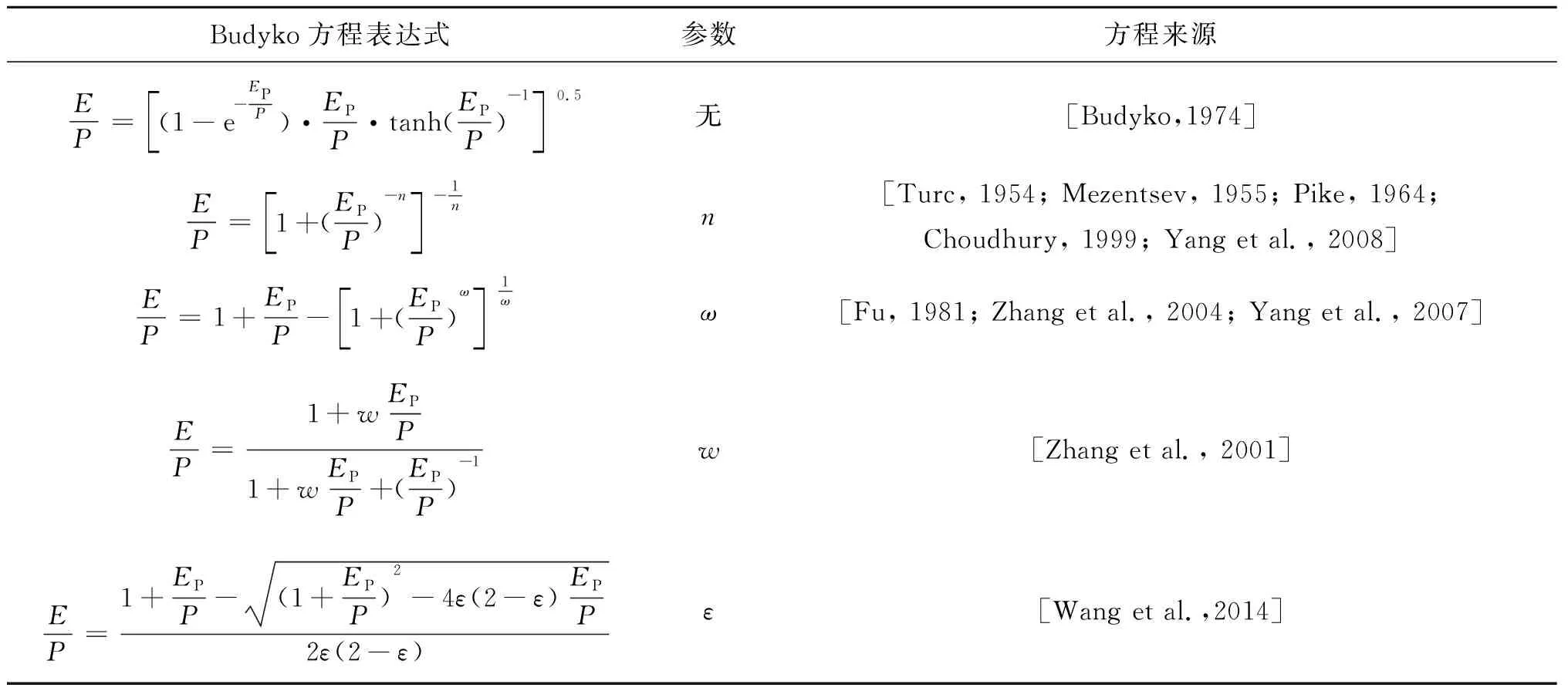
表1 多种形式的Budyko方程表达式

以Wang[17]依据相似性假设推导的Budyko方程表达式为参考，Budyko曲线上下限示意图如图2所示。当参数ε=1时，Budyko曲线的上限条件为：

(1)

当ε=0时，Budyko曲线则达到下限，此时

(2)

式中，R为径流深。

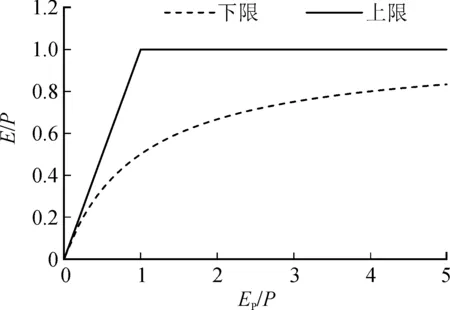
图2 Budyko方程曲线上下限示意图Fig.2 Upper and lower bounds of Budyko equation curve

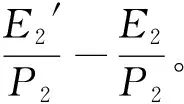
(3)

式中，ΔR为径流深变化总量；ΔRh为人类活动对径流深变化的贡献量；ΔRc为气候变化对径流深变化的贡献量。ΔRc和ΔRh可以是正的，也可以是负的。

图3 定量分解气候变化和人类活动对径流变化贡献的示意图Fig.3 Budyko curve and diagram showing the direct human and climate impacts on runoff

3 结果分析与讨论

3.1 水文气象要素变化趋势分析

采用Mann-Kendall (M-K)秩次相关检验法对小理河流域的径流深、降水量和潜在蒸散发量时间序列的变化趋势进行分析，结果如表2和图4所示。由图可知，径流深变化呈不显著下降趋势；降水量在20世纪90年代之前维持在300～500 mm之间，变化平稳，1995年左右出现短暂下降，随后在本世纪初回升，呈不显著上升趋势；潜在蒸散发量对环境的响应比较敏感，所以波动起伏明显，但总的来说维持在1000～1200 mm左右，呈不显著下降趋势。综合小理河流域水文气象要素变化规律，气候要素中降水量和潜在蒸散发量分别有上升和下降趋势，但径流深的变化却呈下降趋势，这意味着气候变化不是该流域径流变化唯一的影响因素，人类活动可能也是小理河流域径流深减少的重要原因，需进一步深入分析辨识气候变化和人类活动对径流变化的贡献。

表2 小理河流域水文气象要素M-K趋势检验表

Tab.2 Results of M-K test for hydrometeorologicalelements in Xiaolihe basin

水文气象要素统计量U趋势性显著性径流深-1.08下降不显著降水量0.59上升不显著潜在蒸散发量-0.22下降不显著

注：显著性水平α=0.05。

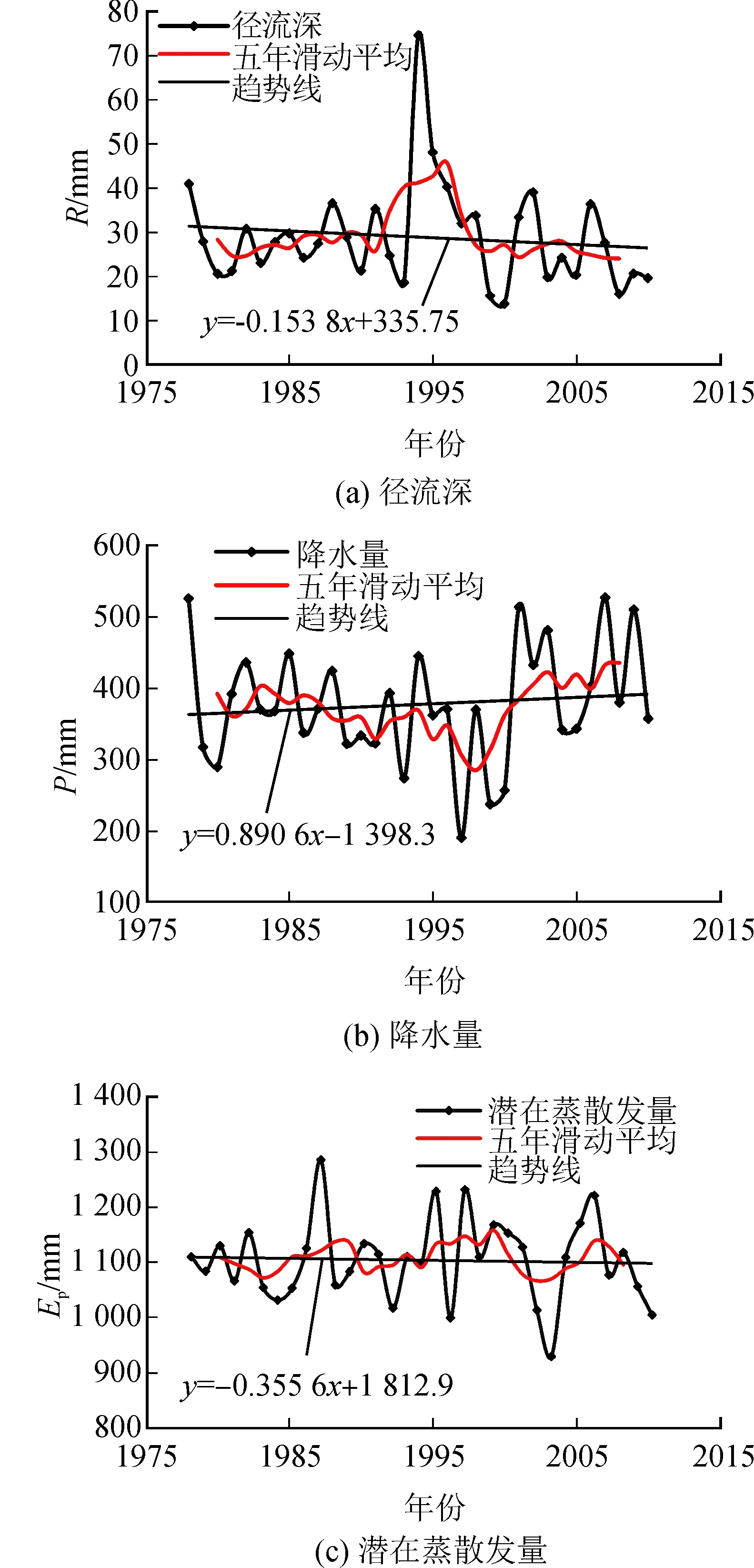
图4 小理河流域水文气象要素变化趋势分析 Fig.4 Change curves of hydrometeorological elements in Xiaolihe basin

3.2 径流深变化突变点的确定

有序聚类法[18]又称最优分段法，该方法是由费歇在1958年提出的，其实质是求最优分割点，使同类之间离差平方和最小，而类与类之间离差平方和最大。有序聚类法是提取水文序列突变点的一种常见方法。传统的T检验法是对变异点的显著性进行检验的方法，并不能用来寻找变异点。雷红富[19]提出了既可以寻找变异点又可以检验变异点显著性的滑动T检验法。综合有序聚类法和滑动T检验法对小理河流域径流变化进行突变分析，结果如图5和图6所示，均表明小理河流域径流深序列的突变点为1998年。

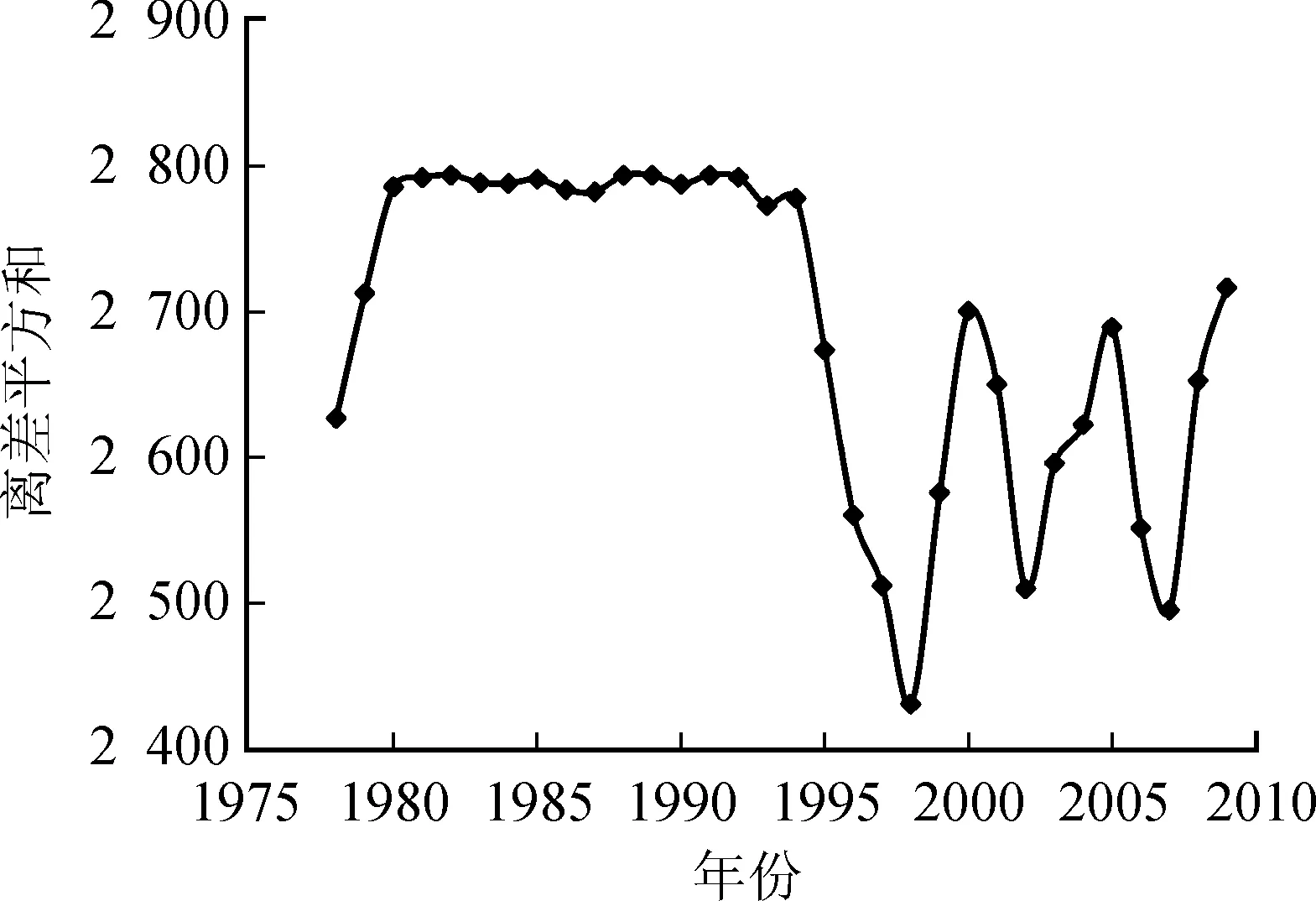
图5 年径流有序聚类法分析曲线Fig.5 Sequential clustering curve of runoff

图6 年径流滑动T检验分析曲线Fig.6 Moving T test curve of runoff

3.3 气候变化和人类活动对径流变化的贡献分析

以1998年为时间节点，划分1978—1997年为基准期，1998—2010年为变化期，且为了满足水量平衡方程，降水量、潜在蒸散发量、径流深数据均采用5年滑动窗口计算处理，经率定，本文所采用的Budyko方程中的参数ε为1.47。

由于Budyko方程中的参数ε由基准期的数据序列率定，代表 1978—1997年的多年平均水平的A点(3.04，0.91)必定落在曲线上(如图7所示)，若仅有降水量及潜在蒸散发量发生变化，A点应沿曲线移动至C点(2.76，0.90)，但实际情况是代表1998—2010年的多年水平的B点位于A点的左上方。1978—1997年多年平均径流深为31.76 mm，1998—2010多年平均径流深为24.70 mm，相对减小了22.23%，根据式(3)计算，Rh为-13.70 mm，Rc为6.64 mm。说明气候因素的变化对径流深的贡献是使径流深增加6.64 mm，大规模的直接人类活动使径流深减小了13.70 mm，两者的综合作用使径流深仅减小了7.06 mm。小理河流域人类活动的影响促使径流深减小了43.14%，而气候因素的变化对径流深的影响抵消了20.91%，与气候变化的影响相比，人类活动是影响该流域径流变化的主要因素。

图7 小理河流域径流变化归因分析Fig.7 Contribution analysis of runoff change in Xiaolihe basin

3.4 讨 论

王随继[20]提出累积量斜率变化率比较法可用于确定气候变化和人类活动对径流变化的贡献，黄生志[21]、郭爱军[22]等也通过实例验证了该方法可以应用在干旱半干旱地区河流径流变化及其影响因素的定量评估中。现利用累积量斜率变化率比较法定量分析小理河流域气候变化和人类活动对径流变化的贡献，与Budyko方程定量分析的结果进行比较，从而探讨Budyko方程定量分析方法在黄土高原地区的适用性及可靠性。

由径流深序列的突变点(1998年)可以将小理河流域径流深、降水量、潜在蒸散发量的时间序列分别划分为两个不同时期，即1978—1997年和1998—2010年，求出累积径流深、降水量、潜在蒸散发量不同时期的累积量斜率，如表3所示，根据斜率变化率的比值可计算得出降水量和潜在蒸散发量对径流深变化的贡献分别是-70.46%和5.03%，即降水量的变大促使径流深增加70.46%，潜在蒸散发量的变小促使径流深减小5.03%，两者的共同作用为气候变化对径流深变化的贡献，为-65.43%，所以人类活动对径流深变化的贡献为165.43%。此处的贡献是指各影响因素的贡献相对于径流深变化量的占比。由于1998—2010年的多年平均径流深相对于1978—1997年减小了7.06 mm，故可计算出气候变化使径流深增加了4.62 mm，其中降水量使径流深增加了4.97 mm，潜在蒸散发量使径流深减小了0.35 mm，而人类活动使径流深减小了11.68 mm。

表3 小理河流域累积径流深、降水量、潜在蒸散发量的斜率变化

对比Budyko方程定量分析方法，两种计算方法对气候变化和人类活动的贡献量的偏差为2.02 mm，但结果近似，即气候变化使径流深增加，而人类活动抵消了气候变化的影响，使径流深总体上减小了7.06 mm，这两种方法均认为人类活动是导致径流深减小的主要驱动因子。

实际上，自20世纪70年代以来，国家在黄土高原地区开展了大面积、大规模的生态环境建设和水土流失综合治理措施，小理河流域采用了坡面造林、种草与修建淤地坝相结合的治理手段，其中淤地坝的减洪减沙作用比较明显，图8为小理河流域1978—2010年淤地坝的修建情况。可以看出，1998年前后，淤地坝数量激增是导致径流减小的主要人类活动，当然，伴随着社会经济的发展，逐步开展的各项经济活动增加了过程用水，这亦是径流减小的原因所在，可见，要维护小理河流域水资源的可持续发展，需要充分合理规划各项工农业生产及水保工程建设。

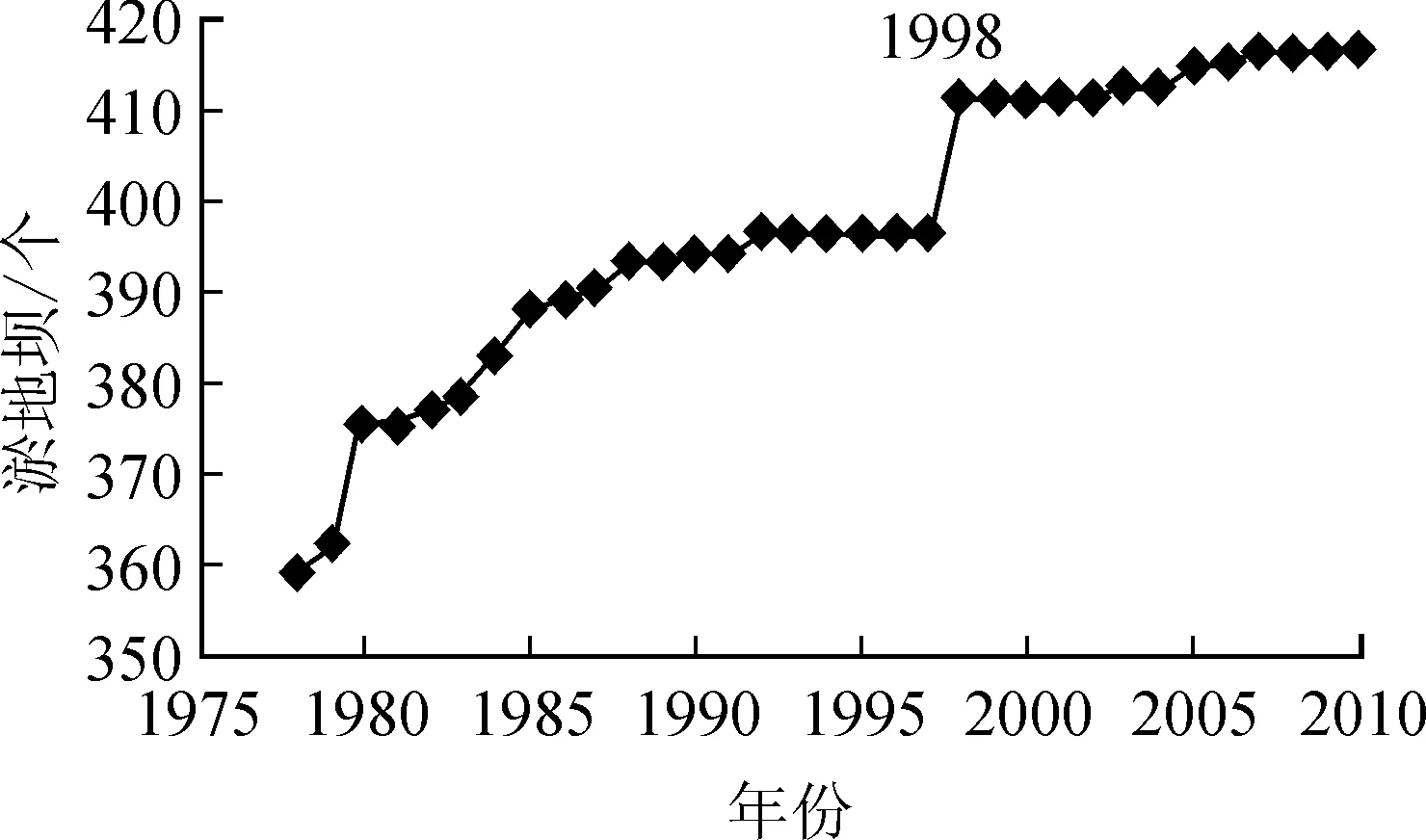
图8 小理河流域淤地坝建设情况Fig.8 Warp land dams in Xiaolihe basin

目前，定量分析环境变化对径流变化的贡献时，气候因素一般仅考虑降水量，这就导致能量供给(由潜在蒸散发量表征)的作用被忽视。通过对小理河流域径流变化影响因素的研究，恰恰说明水分供应和能量供给都是气候变化过程中的重要环节，两者缺一不可。Budyko方程兼顾了降水量和潜在蒸散发量的作用，将降水量、潜在蒸散发量、实际蒸发量之间的关系用简洁的方程式进行描述，其定量计算结果与累积量斜率变化率比较法接近，从而佐证了Budyko方程在黄土高原地区的适用性及可靠性。

环境变化对径流变化的贡献是众多专家学者关注的热点，也是水文序列分析中的难点，Budyko方程着眼于气象水文要素之间密切的相互关系，无疑于为水文过程对环境变化的响应和定量计算拓展了新的思路。本研究的定量分析方法基于两个假设：①如果没有人类活动的影响，当EP/P改变时，E/P也将改变，但仍然处于同一条Budyko曲线；②降水量和潜在蒸散发量的变化可能是自然气候变化造成的，但全球变暖、城市化、城市热岛效应、大规模灌溉等人类活动也能诱发降水量和潜在蒸散发量的变化，气候、人类活动和水文系统的关系是错综复杂的，因此，该理论中的人类活动应该是对径流变化产生影响的直接人类活动，不包含间接造成降水量和潜在蒸散发量变化的人类活动。

此外，Budyko方程中参数ε的物理意义研究、Budyko方程是否可以处理涉及更多变量的数据集、Budyko方程对预测未来气候变化是否具有参考价值等仍需要更深入的探索。

4 结 论

本文利用小理河流域1978—2010年的降水量、潜在蒸散发量及径流深等资料，基于Budyko水热耦合平衡方程，考虑气候因素中水分供应和能量供给两方面对径流的影响，结合人类活动资料，分析计算了不同影响因素对小理河流域径流变化的贡献程度。

1) 分别使用有序聚类法和滑动T检验法对小理河流域径流深序列进行突变检验，两种方法的检验结果均表明，年径流深序列的突变发生于1998年。小理河流域人类活动的资料也证实了这一结论，1998年该流域淤地坝修建数量陡然增加，剧烈的人类活动对小理河流域的下垫面环境造成了不可忽视的影响。

2) 以1978—1997年为基准期，率定Budyko方程的参数ε为1.47。计算结果表明：1978—1997年多年平均径流深为31.76mm，1998—2010年多年平均径流深为24.70mm，减小了22.23%，其中人类活动的影响促使径流深减小了13.70mm，气候因素变化的影响促使径流深增加了6.64mm，因此，人类活动是导致径流深减小的主要驱动因子。

3) 利用累积量斜率变化率比较法定量分析了小理河流域气候变化和人类活动对径流深变化的影响，人类活动使径流深减小了11.68mm，气候变化使径流深增加了4.62mm，其中降水量使径流深增加了4.97mm，潜在蒸散发量使径流深减小了0.35mm。累积量斜率变化率比较法的计算结果证明了Budyko方程定量分析结果的可靠性以及Budyko方程在黄土高原地区的适用性。