基于冗余度和方差的P-Cycle圈构造算法的研究

孙 强，李德莉，任 叶

(北京交通大学电子信息工程学院，北京 100044)

网络生存性方案追求的目标是快速的恢复速度和较高的资源利用率。从未来网络结构来讲，高速铁路光传送网的网络结构会逐步复杂化；从网络传输的业务种类来讲，其传输的业务会逐步多样化；从客户需求来讲，客户的大带宽、大颗粒业务需求也对网络提出了更高的要求[1]。研究网络生存性、可靠性的目的，是为了在发生网络故障后，使故障业务能尽快倒换到提前为其设置的保护路径传输，减少业务中断时间及其给网络运营带来的影响，提高网络质量，避免因为不能快速恢复业务传输而给铁路运行带来巨大损失，保障乘客生命安全。

以牺牲带宽来换取保护是环恢复技术的较大特点，文献[2]为了避免用200%～300%的冗余带宽进行保护，构造一个Hamiltonian环来连接网络中的每一个节点，但可能会造成保护带宽的利用率不高。文献[3]针对上述缺点，提出建立多个小环来覆盖网络中所有节点，不同小环可通过同一个节点，因此有效提高了备份带宽的利用率。文献[4]为了降低节点保护环的ILP容量需求，提出ILP设计模型。文献[5]针对全光网络有望发展为网状网结构的趋势，提出P-Cycle保护的概念，P-Cycle保护同时结合了环网保护倒换快与网状网选路灵活的优点，资源利用率较高。当通过ILP算法来实现P-Cycle保护时会需要较长的时间，文献[6]提出提前选择出可用的圈来降低运行ILP算法所需时间，进而压缩保护过程所需时间，不过这需要在选择前列举网络中所有的P-Cycle，工作量较大，不能保证准确率，关键还会影响算法最终的结果。文献[7]为避免列举P-Cycle，提出跨接链路算法SLA(Straddling Link Algorithm)，但该算法的保护效率与资源利用率较低，因为它构造的圈只能包含一条跨接链路。

总之，P-cycle保护以环结构为基础，利用网络中的空闲资源提前为网状网中的业务设置保护通道[8]，其不同于传统环保护方案最大的特点在于，不仅可以为环上链路的业务提供一倍的保护资源，还可以为跨接链路的业务提供两倍保护资源，资源利用率高[9]。本文提出RVPA P-Cycle构造算法，以冗余度、方差为圈扩展标准，降低为保护网络中所有业务请求所需的P-Cycle数量与资源占用率，使网络资源得到均衡的同时减少了网络保护倒换时间。

1 RVPA算法

之前提出的P-Cycle构造算法只计算扩展候选圈的冗余度，以致于在最初圈扩展时，P-Cycle的圈上链路、跨接链路未得到保护的工作容量方差及大小差距较大，使进一步圈扩展覆盖的链路中，有部分链路上的工作容量均已保护完，而其他链路上还有很多没被保护的工作容量，为使这部分工作容量也得到保护，就需要设置更多的圈，占用更多的空闲容量，资源利用率不高。因此，本文提出RVPA圈构造算法来改善POCA算法的P-Cycle保护效果，它在圈扩展时以所有候选圈上未保护工作容量的方差、冗余度两个指标为比较标准，选择两者都满足条件的圈作为本轮最终扩展圈，有效限制网络保护所需圈个数；同时通过网络未保护链路比率UPL、冗余度、参数M来限制扩展圈长度，使圈个数与圈上节点数做到有效均衡，仿真对比分析在不同M取值下RVPA算法、已有POCA算法[10]的性能，并为RVPA算法选择其性能最优时对应的M值。

1.1 RVPA算法应用举例

POCA算法单纯以冗余度为标准进行圈扩展，为了改进此不足，以及完善其只通过选取取值在某一范围内的参数K来限制圈长度，而并未选择、比较出算法在性能最优时的K值的缺憾，本文提出RVPA算法，它同时以方差、冗余度为圈扩展标准，并对比分析两算法在不同M取值下的仿真结果，最终为RVPA算法选择、设置最优M值。

图1中的网络拓扑包含7个节点、11条链路，链路权重代表该链路承载的业务请求数量，以该网络拓扑为例说明POCA、RVPA算法的保护过程。

图1 RVPA算法与POCA算法

步骤1以3-6链路为基础构造最小圈，因为该链路上未保护工作容量最大，具体算法构造过程见表1。

表1 最小圈构造

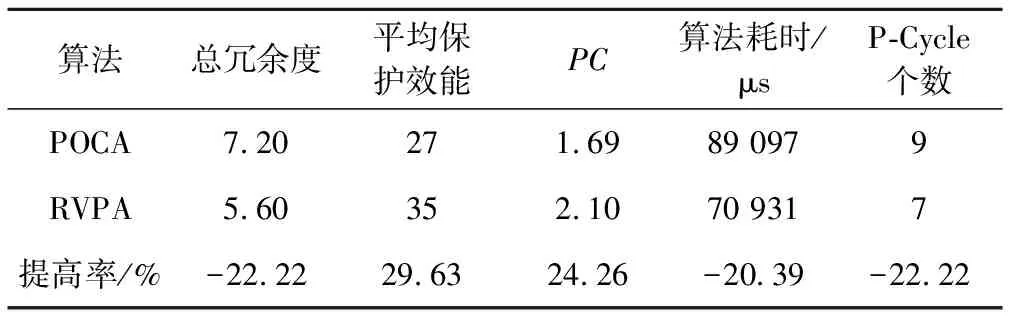
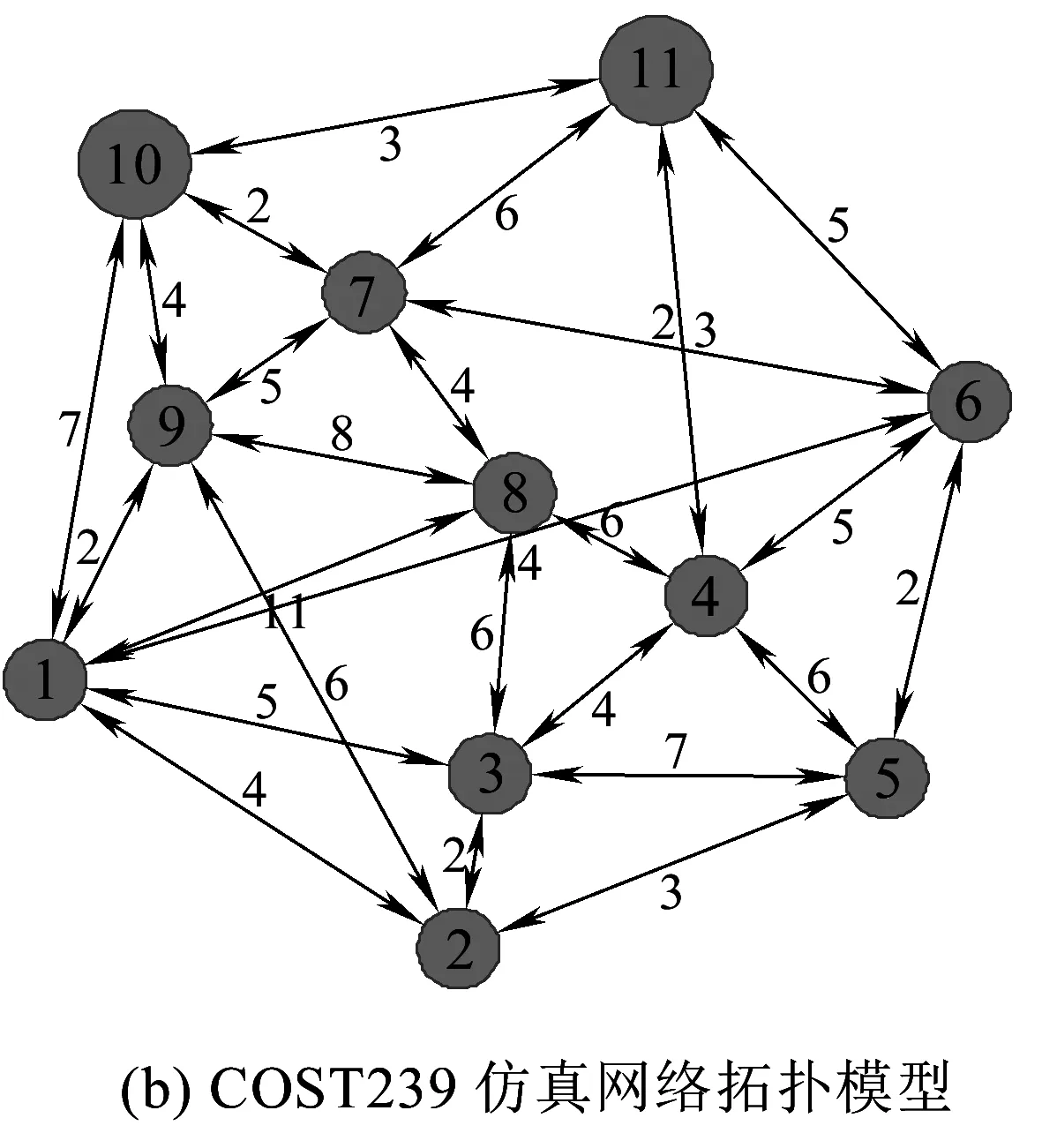
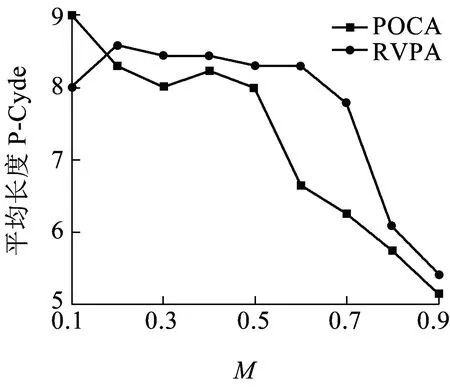
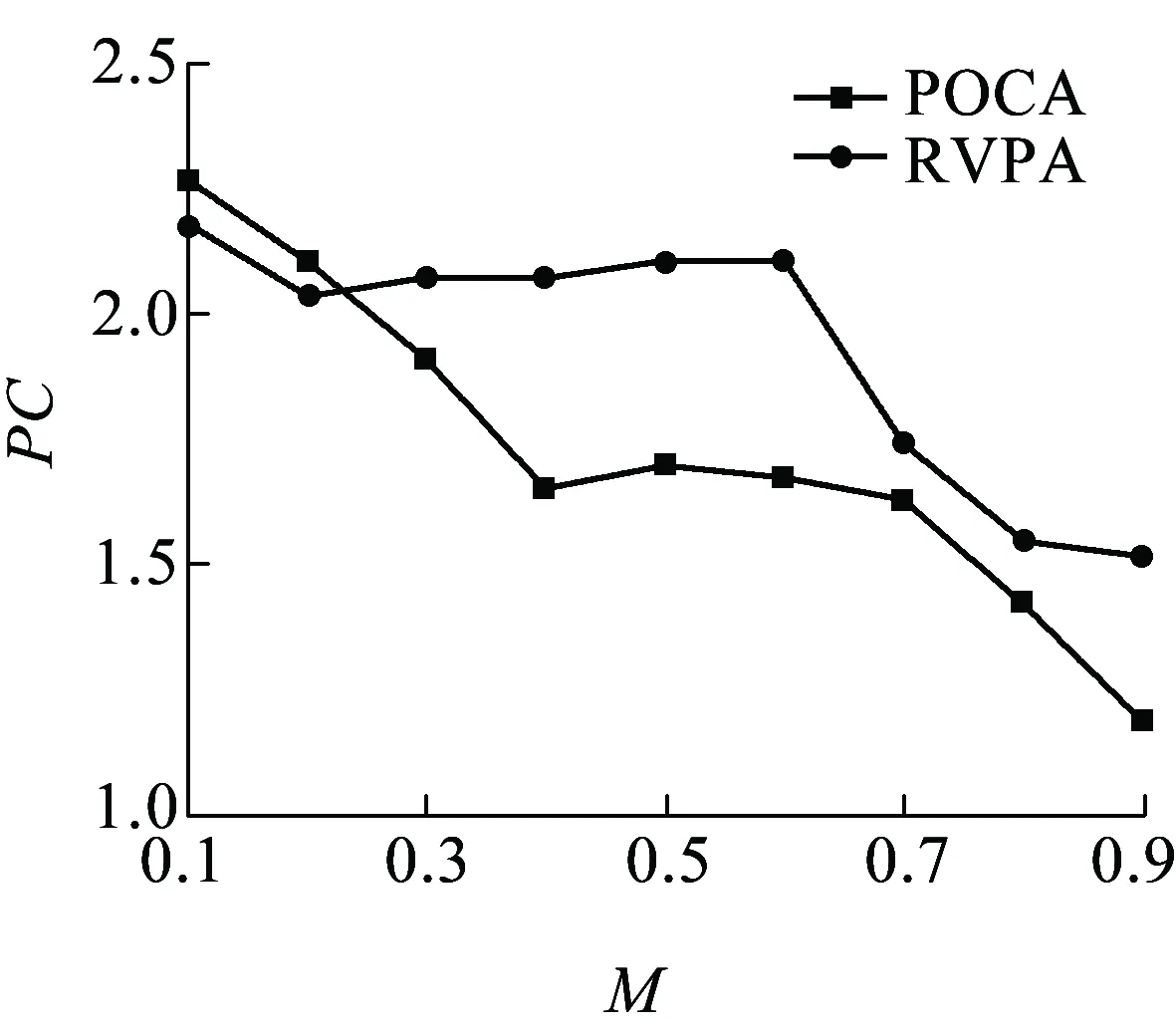
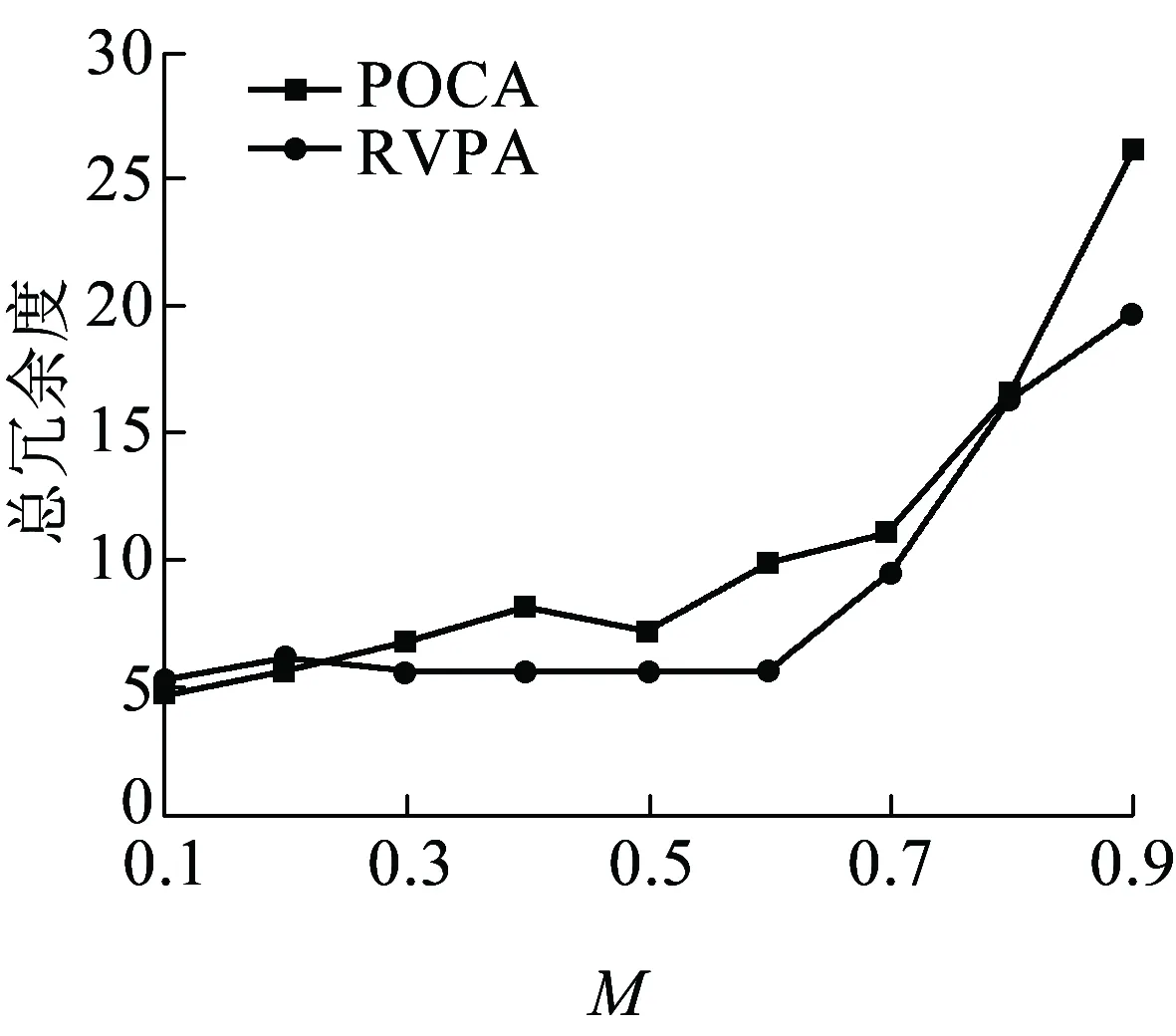
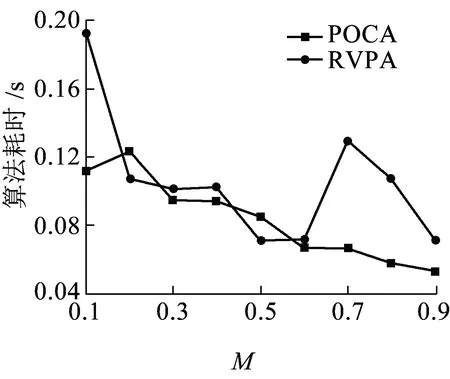
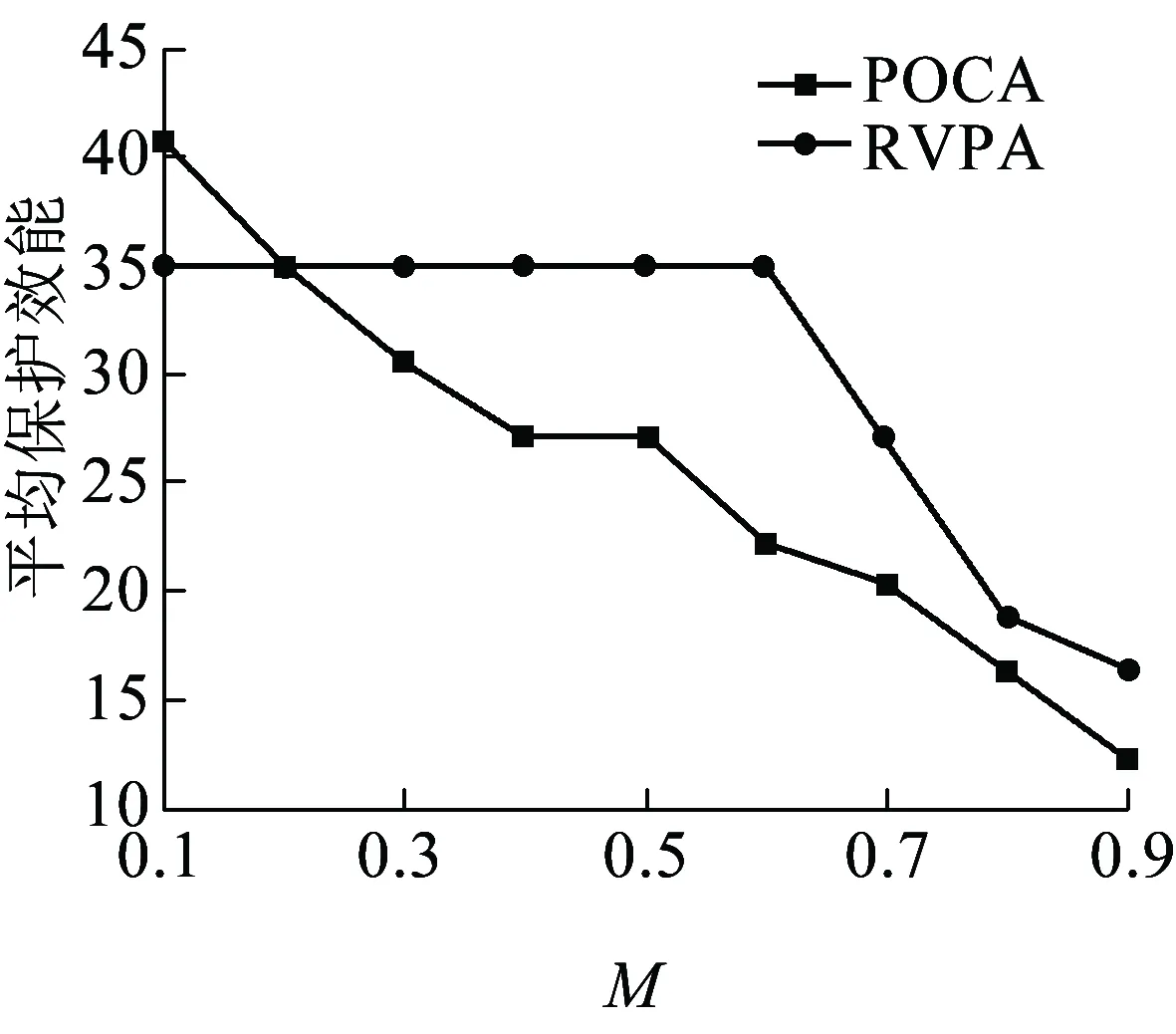
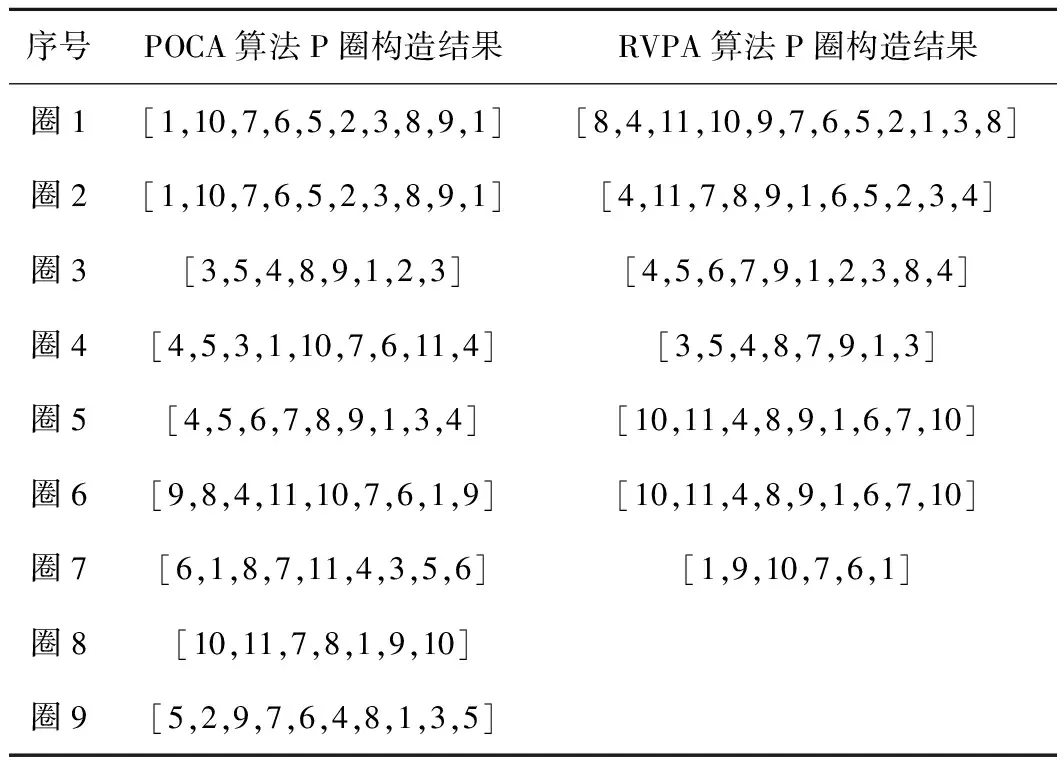
步骤2设定参数M=0.5，得到此时全网UPL为0.85，不满足UPL

步骤3以最小圈C3为基础开始圈扩展，具体过程见表2。

表2 最小圈C3扩展表

POCA算法圈扩展结果会三选一，而RVPA算法圈扩展结果为5-3-1-4-6-5，但其未保护链路比率不满足小于其冗余度的条件，所以需在第一次圈扩展结果5-3-1-4-6-5的基础上继续进行圈扩展，当达到扩展圈的未保护链路比率同时小于参数M和冗余度时，则本次P-Cycle构造完成。然后更新本轮构造P-Cycle覆盖链路的工作容量，即圈上链路减1、跨接链路减2，之后进行新一轮的构造最小圈、最小圈圈扩展、扩展圈配置。

1.2 RVPA算法参数

算法参数说明见表3。

表3 算法参数说明

1.3 RVPA算法性能指标

算法性能评价指标说明如下。

(1)算法计算时间：即算法运算时间，该值越小越好，它是网络故障后受损业务保护倒换时间的一部分。

(2)PC：该值越大越好，是被保护的工作容量除以为它配置保护消耗的空闲容量。

(3)P-Cycle个数：指为保护全网工作容量所需圈的总个数，它越小越能降低算法计算时间与圈配置错误的风险。

(4)冗余度R(p)：PC值的倒数，越小越好，用于评价P-Cycle资源利用效率[10-11]，即配置P-Cycle使用波长总数除以圈上、跨接链路上被保护波长的和。

( 1 )

式中：XP,i为圈的各边能保护的工作容量大小，其取值由链路i与圈的关系决定，i为圈上边时其值取1，i为跨接边时其值取2，当两者都不是时其值取0。

(5)总冗余度：该值越低表示网络资源利用率越高，则可用较少空闲容量来保护全网工作容量。

(6)P-Cycle平均保护效能：单个P-Cycle保护能力的象征，为整个网络配置的所有P-Cycle可保护的工作容量与圈个数的比值，该值越高则网络资源利用率越高[12]。

2 RVPA算法流程

算法输入：G=(N，L)、Wi、ui、M。

算法输出：各项性能指标，如算法计算时间、PC值、P-Cycle个数、冗余度R(p)、总冗余度、P-Cycle平均保护效能，以及算法P-Cycle构造结果。

算法具体步骤如下：

步骤1为G配置业务请求，分配工作容量，初始化ui=Wi(i∈L)，m=1。

步骤2在G中寻找承载最大工作容量的链路L1，其两个端点分别为l1、l2，删除L1，分别以l1、l2为起始节点、目标节点，运行Dijkstra算法寻找最短路径L2，将L1与L2首尾相连构造最小候选圈C1；删除L2，重复上述寻找最短路径过程，若可再次找到最短路径L3，则将L3与L1首尾相连构造最小候选圈C2，且L3与L2首尾相连构造最小候选圈C3，可得L1为C3跨接链路；若没找到最短路径L3，则设L3=L1；将3个候选最小圈中冗余度最小的圈记为Cmin，其最小冗余度值记为Rmin。

步骤3若此时网络的未保护链路比率UPL满足UPL

步骤4以所有圈上边为基础依次进行圈扩展，即删除圈上边i(i≥1)，运行Dijkstra算法找到与该边链路分离的最短路径Di，此时Di作为圈上边与原有圈构成了以第i条链路为跨接边的新候选圈，计算该新候选圈的未保护工作容量的方差并存为V(c+i)、冗余度存为R(c+i)，i=i+1进行循环，直至i不能再增加，即所有圈上边都扩展后转至步骤5。

步骤5依次分别比较步骤4中储存的R(c+i)、V(c+i)与R1、V1的大小，若满足V(c+i)≤V1且R(c+i)≤R1圈扩展条件，则V1=V(c+i)、R1=R(c+i)，并找到满足上述扩展条件的最优圈，然后储存为Cnew并释放其他扩展候选圈；若此时网络的UPL满足UPL

步骤6更新G工作容量矩阵(工作容量为0的链路不更新)，即圈上链路工作容量减1、跨接链路工作容量减2，直到所有的工作容量都得到保护时算法停止运行，否则转至步骤2，进行算法迭代，更新m=m+1。

算法流程如图2所示。RVPA算法对于圈长度的约束力度通过参数M(0.1

图2 RVPA算法流程

3 RVPA算法仿真结果与分析

3.1 仿真环境配置

COST239含11个节点、26条边，节点平均度为4.73，为网状网络拓扑模型，生存性技术P-Cycle适于保护网状光网络，如图3所示，本文选用泛欧COST239[13]为仿真网络拓扑，图3(a)节点名称与具体地理位置相对应[14]，图3(b)链路权重表示该链路上的工作容量(单位为波长的个数)，假设在仿真过程中，已知COST239工作容量矩阵，且其节点可全波长变换，业务流向双向对称。

图3 仿真网络拓扑

3.2 仿真结果

图4～图9显示了M从0.1开始以步长0.1为单位增长到0.9时，两算法各性能指标的取值情况。

由图 4可知，两种算法所需P-Cycle个数在M取值依次增长时，均整体呈上升趋势，且POCA算法增长率较大，由M=0.1时的取值6增长到最大值20，而RVPA算法M取0.1～0.6时的恒定值7增长到最大值15，所需P-Cycle个数降低33.33%。M=0.5时POCA、RVPA算法所需P-Cycle个数分别为9、7，PVPA算法比POCA算法所示P-Cycle个数低22.22%，由此可见，RVPA算法性能比POCA算法性能更加稳定，性能更优。

如图5可知，当M取值依次增长时，保护全网相同业务请求需要的圈数量与圈平均长度整体相反。当M取0.5时，圈平均长度取值适中，满足要求。

图5 不同M取值下P-Cycle平均长度

由图 6可知，两种算法的PC值在M取值依次增长时，RVPA算法要整体高于POCA算法取值；且在M=0.5时，POCA、RVPA算法的PC取值分别为1.69、2.10，RVPA算法取值大，比POCA算法提高24.26%。由此可见，RVPA算法性能更优。

图6 不同M取值下PC值

图7 不同M取值下的总冗余度

由图 7可知，两种算法的总冗余度在M取值依次增长时，RVPA要整体小于POCA算法取值，但两者取值均呈整体上升趋势，且M=0.5时，POCA算法取值为7.2，而RVPA算法取最小值5.6，PVPA算法比POCA算法降低22.22%。由此可见，RVPA算法性能更优。

运行环境不同则算法耗时也不同，算法运行耗时呈随机分布，如图8所示。由图8可知，RVPA算法耗时在M取0.2、0.5时少于POCA算法耗时；且当M=0.5时，RVPA、POCA算法耗时分别为0.070 931、0.089 097 s，PVPA算法比POCA算法耗时降低20.39%。

图8 不同M取值下的算法耗时

新增方差运算会增加算法复杂度，延长算法耗时，但在保护相同业务请求时，RVPA算法所需P-Cycle个数少于POCA算法，而且单个P-Cycle上节点数较少，降低了算法整体耗时。

图9 不同M取值下的平均保护效能

由图 9可知，两算法的平均保护效能在M取值依次增长时，均整体呈下降趋势，且RVPA算法取值由M取0.1～0.6时的最大值35下降，但其整体取值与最小取值大于POCA算法的整体取值与最小值。M=0.5时，POCA、RVPA算法平均保护效能分别取值27、最大值35，RVPA算法比POCA算法提高29.63%，RVPA算法性能更优。

3.3 仿真结果分析

表4中显示了在M=0.5时RVPA算法的各指标取值与不同M取值下各指标的平均取值对比情况。除P-Cycle平均长度外，其他性能指标均是PVPA优于POCA，这是因为M取较小值时算法的约束力度较高，所以构造出的圈上节点数量较少，拉低了平均值，但圈数量偏多。

表4 RVPA算法性能汇总

M=0.5对应算法最优性能，此时两算法的圈构造结果见表5。

表5 M=0.5时两算法圈构造结果

由表 5可知，当M取0.5时，POCA、RVPA算法在保护相同的业务请求时，所需要P-Cycle个数分别为9、7，而且后者的P-Cycle构造结果平均长度较小，整体性能更优。图10是以表5中第7个圈为例在COST239网络拓扑中的构造结果。

图10 P圈构造结果说明示例

4 结论

本文提出RVPA算法，通过求取扩展候选圈上未保护工作容量的方差，在圈扩展时以所有候选圈上未保护工作容量的方差、冗余度两个指标为比较标准，当两者同时满足圈扩展条件时，选该候选圈为本次扩展的最终圈，与POCA算法相比有效限制了保护全网工作容量所需圈个数。仿真结果表明，在COST239网络拓扑中，当POCA、RVPA算法保护相同业务请求时，后者在有效降低保护全网所需圈个数的同时，通过参数M限制每个P-Cycle的节点个数，使圈个数与圈长度得到有效均衡，降低全网总冗余度，提高P-Cycle平均保护效能、PC，最终分析可得M=0.5时可达到最优仿真效果。M取0.5时POCA、RVPA算法的各性能指标取值见表6。由表6可知，RVPA算法各项性能指标优于POCA算法。

表6 M取0.5时两种算法性能指标取值

由表6可知，POCA、RVPA算法同一个网络中保护相同的业务请求时，在M=0.5时，PVPA算法比POCA算法的总冗余度降低22.22%，平均保护效能提高29.63%，PC取值提高24.26%，算法耗时降低20.39%，P-Cycle个数降低22.22%。综上可得，RVPA算法性能整体优于POCA算法性能，且M=0.5时RVPA算法保护效果最优。预计到2030年，铁路光传送网的网络结构将朝着网状网格局发展，铁路建设将会基本形成内与外互联互通、县与域基本覆盖、区际之间多路畅通、地市之间快速通达、省会之间高铁连通的局面[15]，故本文提出的适用于网状光传送网的基于冗余度和方差的P-Cycle圈构造算法RVPA，随着P-Cycle保护技术在铁路光传送网中的大力推广，将对铁路光传送网保护技术有一定的借鉴意义。