层状顶板破坏范围及形态研究

罗 霄，李 伟，王振伟

(1.煤炭科学技术研究院有限公司 安全分院，北京 100013； 2.煤炭资源高效开采与洁净利用国家重点实验室(煤炭科学研究总院)，北京 100013；3.辽宁工程技术大学,辽宁 阜新 123000)

我国煤炭资源赋存的多样性决定了开采方式不同，目前井工和露天是主要的煤炭开采方式，但露井联采也在逐渐兴起，它既具备露天矿开采的特殊性，也具备井工开采的特征，尤其是露井联采中的井工开采的巷道遇到层状顶板的问题，急需要深入了解巷道顶板破坏状况，提出支护对策[1]。因为层状顶板物理力学特性具有显著的差异，加之软弱岩层抗拉强度极弱，在垂直地层荷载、水平构造应力及动压影响下，层状顶板于跨中挠度最大处会出现拉裂并发生大范围失稳冒落，严重威胁煤矿的安全生产[2]。露井联采中的井工矿巷道在实际工程中通过工程类比或施工经验来确定层状顶板的支护方案及其参数，缺乏针对巷道层状顶板支护设计的理论依据，导致顶板安全事故频发，使层状顶板发生较大离层甚至破断，表现为支护设计的可靠性低，巷道返修率较高，提高了巷道的维护成本,也影响了煤矿的正常生产。因此，从露井联采中的井工矿巷道层状顶板的破坏范围及形态为出发点，应用高等数学、经典力学、岩体力学及围岩承载圈等知识[3-5]改进平衡拱理论；根据支护的及时性，层状顶板平衡拱分为初始平衡拱和极限平衡拱；基于两帮不同破坏形式得出了平衡拱存在3种形态即：自然平衡拱、隐形平衡拱、扩展隐形平衡拱，也得出了支护时极限平衡拱的矢高，进而确定了锚索长度，这可为层状顶板在支护设计中提供参考依据。同时，也能进一步丰富现有的巷道支护理论，具有极其重要的工程实用价值和理论意义。

1 层状顶板的发育破坏特性

层状顶板主要特征[6]是：不稳定的层状岩层累计厚度大；各层之间物理力学特性各不相同，总体的强度比较低；松散易碎，稳定能力差，整体性较差；顶板各岩层自然赋存形态差异较大，各层间有弱面存在，抗剪强度比较低，容易发生离层脱落。巷道开挖后，围岩应力重新分布，顶板在垂直地层荷载和水平构造应力综合作用下发生弹塑性变形破坏后冒落[7]，如图1所示。

1—自然平衡拱；2—隐形平衡拱；3—扩展隐形平衡拱图1 层状顶板变形破坏示意

露井联采中井工矿巷道层状顶板的变形破坏过程及形成不同形态的平衡拱通常包括以下几个阶段：

(1)巷道进行开挖后，层状顶板下层由以前的三向应力受力状态转变为二向应力受力状态，层状顶板各层所受应力发生重分布，进入弹性阶段，出现略微挠曲变形，在此时软弱夹层会出现不均等裂纹。

(2)若不及时支护，层状顶板应力进一步释放，顶板在垂直荷载和水平荷载的共同作用下，挠曲变形进一步加剧，其中的软弱夹层逐渐破坏，层状顶板跨中开始出现裂纹，此时帮部维持稳定，未发生明显破坏。由于水平构造应力及地应力继续联合作用，导致顶板跨中下侧岩石开始断裂垮落，逐渐冒落为一个无支护条件下的初始平衡拱，此时也属于自然平衡拱的初始状态。若继续不及时支护，巷道两帮与顶板肩部压应力高度集中，导致帮部岩层由于压应力及应变过大开始破坏，此时顶板上方继续垮落形成自然平衡拱中的极限平衡拱。当巷道帮部破坏、滑落，形成不同程度的片帮，失去承载上部层状顶板的能力，进而突破自然平衡拱中的极限平衡拱，逐渐冒落成为隐形平衡拱中的初始平衡拱。

(3)若仍然不及时支护，随着层状顶板下部岩层的进一步拉裂和帮部岩体继续破坏片帮，层状顶板各岩层在水平构造应力和垂直地层荷载联合作用下部分岩层挠度越来越大，顶板各层岩体的裂缝很快发育、直至最后变形破坏，其岩体逐次往上冒落，同时巷道帮部岩体破坏范围继续增大，突破隐形平衡拱中的极限平衡拱，最后形成拓展隐形平衡拱中的初始平衡拱及极限平衡拱。根据层状顶板的变形破坏过程及形成不同形态平衡拱的变化特征，若在发生变形破坏各间段采取及时支护措施，则会起到很好的巷道及顶板维护效果，大大降低巷道的维护成本，提高了煤矿安全生产效率。

2 普氏平衡拱学说留存不足与改善

2.1 普氏平衡拱理论的不足之处

20世纪早期，普氏平衡拱学说在某种水平上体现了地下平巷或隧洞顶板冒落的一般规律，但该理论在条件假设和分析推导中尚存在以下几方面的不足[8]：

(1)未考量水平构造力对层状顶板平衡拱的影响。

(2)未考虑巷道帮部片帮形式的多样化。

(3)未考虑层状顶板依次脱落的工程特征。

2.2 层状顶板平衡拱理论的改进

层状顶板由于层与层的厚度不同，加之岩石的各向异性，所有层状顶板变形破坏和冒落具体表现为：

(1)冒落拱从顶板底部逐层向上发育，各层冒落拱形状和高度各不相同。

(2)底层发育的状况影响上层发育，底层发育形成的宽度是上层继续发育时的跨距。

(3)各层冒落拱的形态与高度，决定于各层冒落时的跨距及各层岩性。

针对普氏平衡拱理论存在的问题，将巷道帮部破坏分为单斜面剪切滑移和楔形破坏两种工况[9]，并考虑不同水平构造应力对层状顶板平衡拱形态的影响，分析各种情况下的层状顶板平衡拱的形态及其矢高，为层状顶板在支护设计中提拱参考依据。

3 层状顶板平衡拱呈现状态及矢高

基于上述分析，建立层状顶板在垂直地层荷载和水平构造应力共同作用下的平衡拱力学模型，如图2所示。可以看出，隐形平衡拱和扩展隐形平衡拱较自然平衡拱而言，仅是巷道有效跨度有所差异。为便于分析，在此仅对自然平衡拱的形态及矢高进行研究。

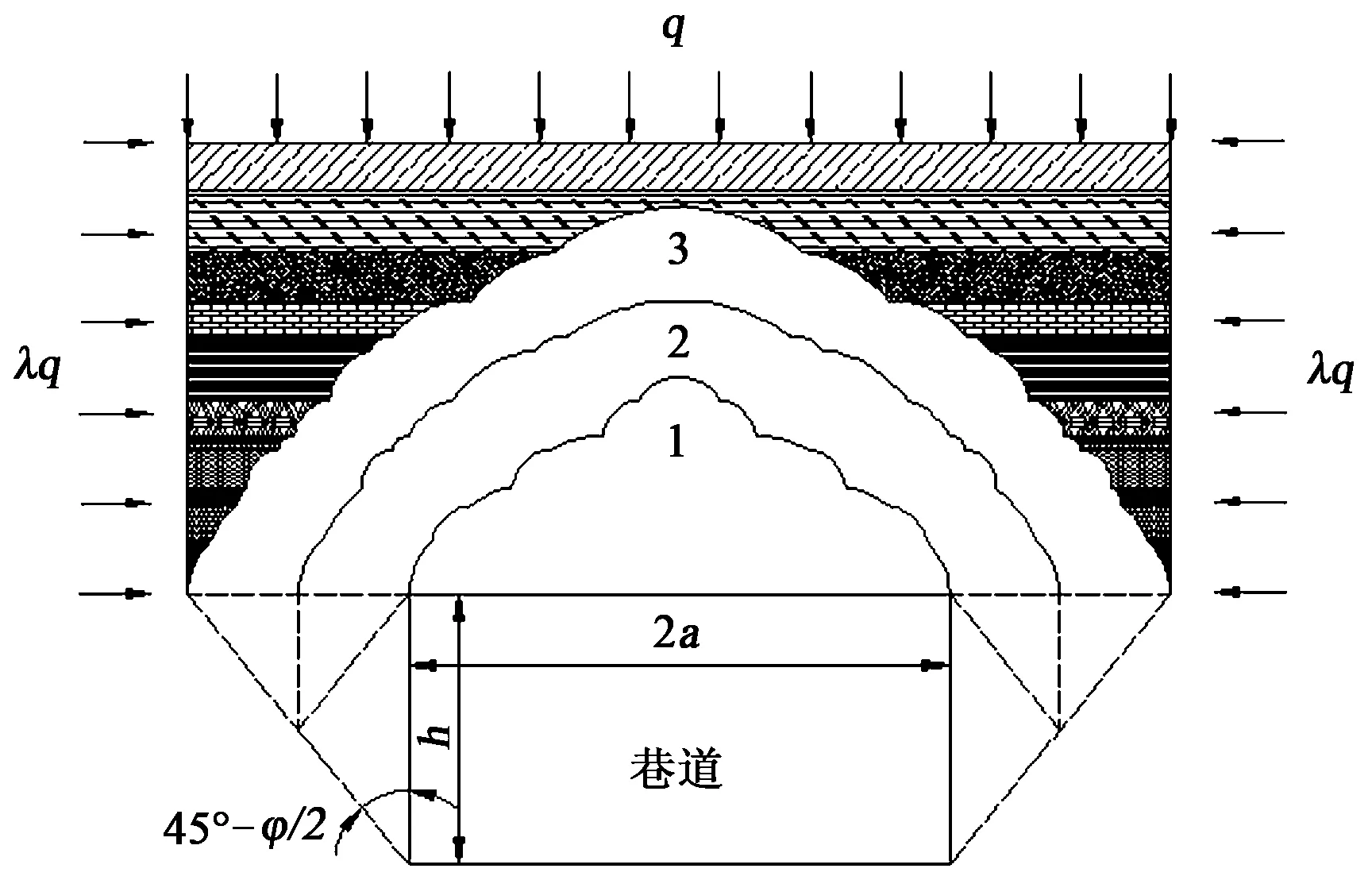
1—自然平衡拱；2—隐形平衡拱；3—扩展隐形平衡拱图2 层状顶板平衡拱力学分析模型

初始自然平衡拱在层状顶板变形破坏并冒落至一定阶段时形成，该平衡拱形成后应当及时采取人为支护，否则该平衡拱将进一步冒落最终形成极限平衡拱，如图3所示。为便于分析，将层状顶板垮落形成的平衡拱轨迹线简化为光滑曲线。

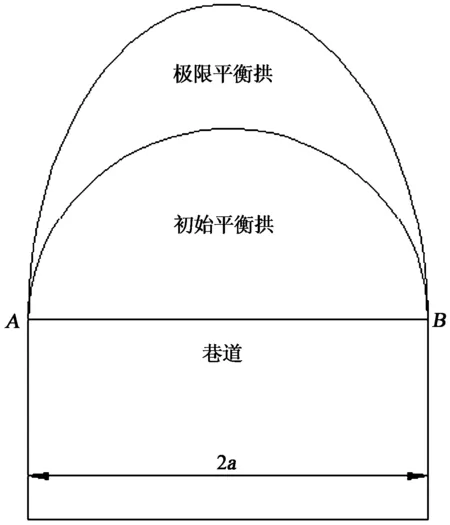
图3 不同稳定状态下的顶板平衡拱形态

3.1 自然平衡拱的形态及矢高分析

3.1.1 初始自然平衡拱的形态及矢高分析[10-11]

为便于研究，取层状顶板自然平衡拱的左半边为研究对像，建立力学模型，如图4所示。

图4 层状顶板自然平衡拱模型

在平衡拱上任取一点M(x,y)，以OM为研究对象。由于平衡拱轴线不能承受拉力，则所有外力对M点的弯矩应为0，即有：

(1)

式中，T为拱顶所受水平切力，N；q为应力，N；λ为水平侧压力系数。

整个左半拱在水平x轴方向受力平衡，则：

T-λqb1-T′=0

(2)

式中，b1为自然平衡拱矢高，m；T′为拱脚所受水平切力，N。

拱脚A受水平切力T′和垂直反力qa的作用，二者合力为W。在水平x轴方向上，拱脚A要维持稳定必须满足：

KT′-qaf=0

(3)

式中，K为安全系数；f为层状顶板下部岩层与两帮界面上的摩擦系数；a为巷道半宽，m。

由式(1)～(3)可得两帮稳定时层状顶板自然平衡拱的方程为：

(4)

讨论不同水平构造应力下的层状顶板自然平衡拱显现状态和矢高：

(1)当λ=0时，由式(4)即有：

(5)

式(5)表明在无侧压时，两帮稳定条件下层状顶板自然平衡拱的方程仍为一抛物线。当x=a，K=2时，初始自然平衡拱的矢高为：

(6)

(2)当0<λ<1或λ>1时，将式(4)化简后得：

(7)

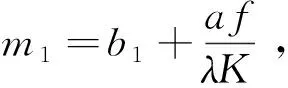
(8)

将x=a，y=b1代入式(4)得：

(9)

解得：

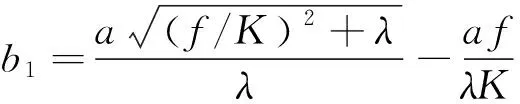
(10)

进而得到：

(11)

式(11)表明，椭圆状自然平衡拱的矢高b1随拱脚处稳定安全系数K的增加而增加。

(3)当λ=1时，由式(4)即得：

(12)

圆的方程，圆心(0,m1)，与顶板AB的距离：

(13)

令式(10)中λ=1，即得圆弧时的拱高：

(14)

式(14)表明，当拱脚处稳定安全系数K和综合摩擦系数f一定时，层状顶板平衡拱的矢高b1与巷道设计半宽a呈正比例关系。

3.1.2 极限自然平衡拱的呈现状态及矢高分析

若不及时支护，层状顶板平衡拱将不断脱落，直至形成抛物线状的极限自然平衡拱。图5为建立的极限自然平衡拱左半部分力学分析模型。任取拱曲线上一点M(x，y)，以OM作为研究对象。对M点取力矩平衡方程仍可得式(1)。左半拱沿水平方向静力平衡，有：

T-λqb2+T′=0

(15)

式中，b2为极限自然平衡拱的矢高，m。

由拱脚平衡可得：

KT′-qaf=0

(16)

式中，摩擦力qaf方向为负。

将式(15)和(16)代入式(1)得：

(17)

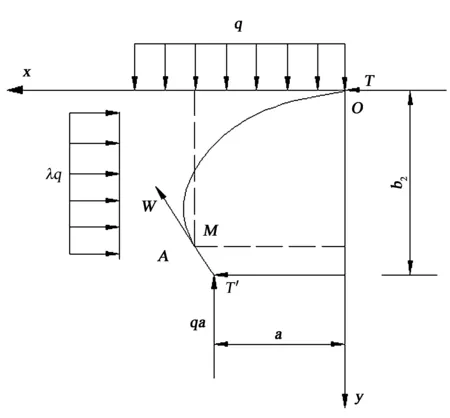
图5 极限自然平衡拱计算模型

对不同侧压力系数下极限平衡拱的形态及其矢高进行讨论：

(1)当λ=0时，由式(17)即有：

(18)

式(18)与无侧压条件下的普氏抛物线形自然平衡拱相似，其中af表示小于0的矢量。将x=a，y=b2，K=2代入式(18)得：

(19)

式(19)与普氏理论所得结论相吻合。

(2)当0<λ<1或λ>1时，将式(17)化简后得：

(20)

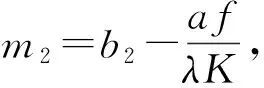
(21)

将x=a，y=b2代入式(17)得：

(22)

式(22)是关于极限平衡拱矢高b2的二次方程，解得：

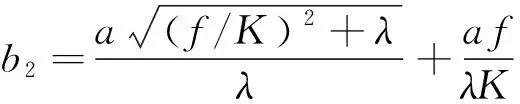
(23)

得到：

(24)

由式(24)可知，拱脚处稳定安全系数K越大，极限平衡拱的矢高b2越小。反之，在垂直反力qa所产生的摩擦力qaf一定下，矢高b2越大，拱脚处越危险，矢高b2越小，则越安全。

(3)当λ=1时，由式(17)即得：

(25)

圆心(0，m2)，与顶板AB的距离为：

(26)

令式(23)中λ=1，得极限自然平衡拱为圆弧拱时的矢高为：

(27)

由式(27)可知，当矿山巷道围岩处于静水压力状态时，若拱脚处的稳定安全系数K和综合摩擦系数f一定时，圆弧状极限平衡拱的矢高b2与巷道半宽a仍成正比例关系。此处，极限平衡拱的矢高可为巷道非稳定情况下，计算出锚索的长度提供依据。锚索计算长度即为：

L=l1+l2+l3

(28)

式中，L为锚索的总长度，m；l1为锚索的外露长度，m；l2为极限平衡拱矢高，m；l3为锚入稳定岩层长度，m。

l3通过下式确定，即：

(29)

式中，K为安全系数，一般取1～3；D为锚索钻孔直径，m；P为锚索的极限拉拔荷载，kN；τr为注浆体与岩体间的粘结力，MPa。

3.2 层状顶板自然平衡拱矢高影响要素分析

由式(23)可以清楚地看出，当其他参数一定时，层状顶板的平衡拱矢高与水平侧压力和巷道跨度密切相关。

3.2.1 不同侧压下层状顶板的平衡拱矢高

根据式(23)，当巷道宽度为4～5m，侧压力系数分别为0，0.5，1.0，1.5，2.0，设坚固性系数f为1.9，安全系数K为2时，层状顶板的平衡拱矢高的计算值如表1所示，由此得到侧压系数与层状顶板平衡拱矢高的关系如图6所示。

表1 层状顶板的平衡拱矢高计算

图6 不同侧压下层状顶板的平衡拱矢高

由表1和图6可以得出：

(1)侧压系数λ对层状顶板平衡拱矢高有明显影响。一定宽度条件下，λ的逐渐变大，平衡拱矢高逐渐减小，λ<1时比λ>1时，矢高明显变大，即层状顶板的破坏范围增大。

(2)随着侧压系数λ的增大，水平构造应力加剧巷道顶板下位岩层的挠曲变形，同时使顶板上位岩层存在隆起趋势。与式(20)所得结论相吻合。

3.2.2 不同巷道跨度层状顶板的平衡拱矢高

根据表1亦可得不同巷道跨度条件下层状顶板的平衡拱矢高的变化曲线，如图7所示。

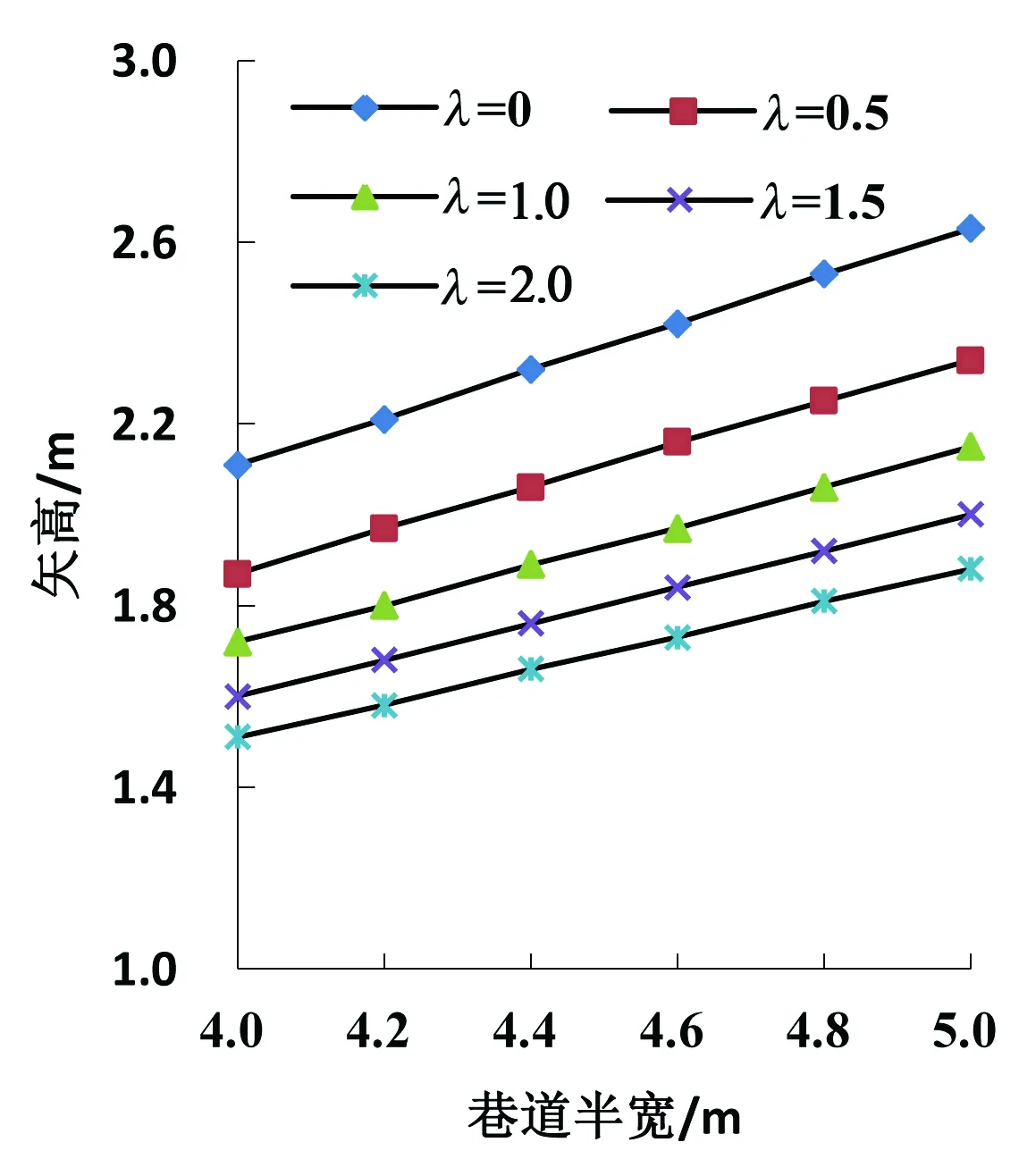
图7 不同巷道跨度下层状顶板的平衡拱矢高

由图7可以得出，当侧压系数相同时，随着巷道宽度的增大，层状顶板的平衡拱矢高逐渐增大。这是由于巷道跨度的增加，由巷道两帮和顶板承载的垂直荷载更大，层状顶板的冒落范围相应增加。

3.3 隐形和扩展隐形平衡拱的形态及矢高分析

图8所示为当巷道帮部失稳时，不同平衡拱下的巷道有效跨度。此时，层状顶板自然平衡拱将进一步演变为隐形平衡拱和扩展隐形平衡拱。

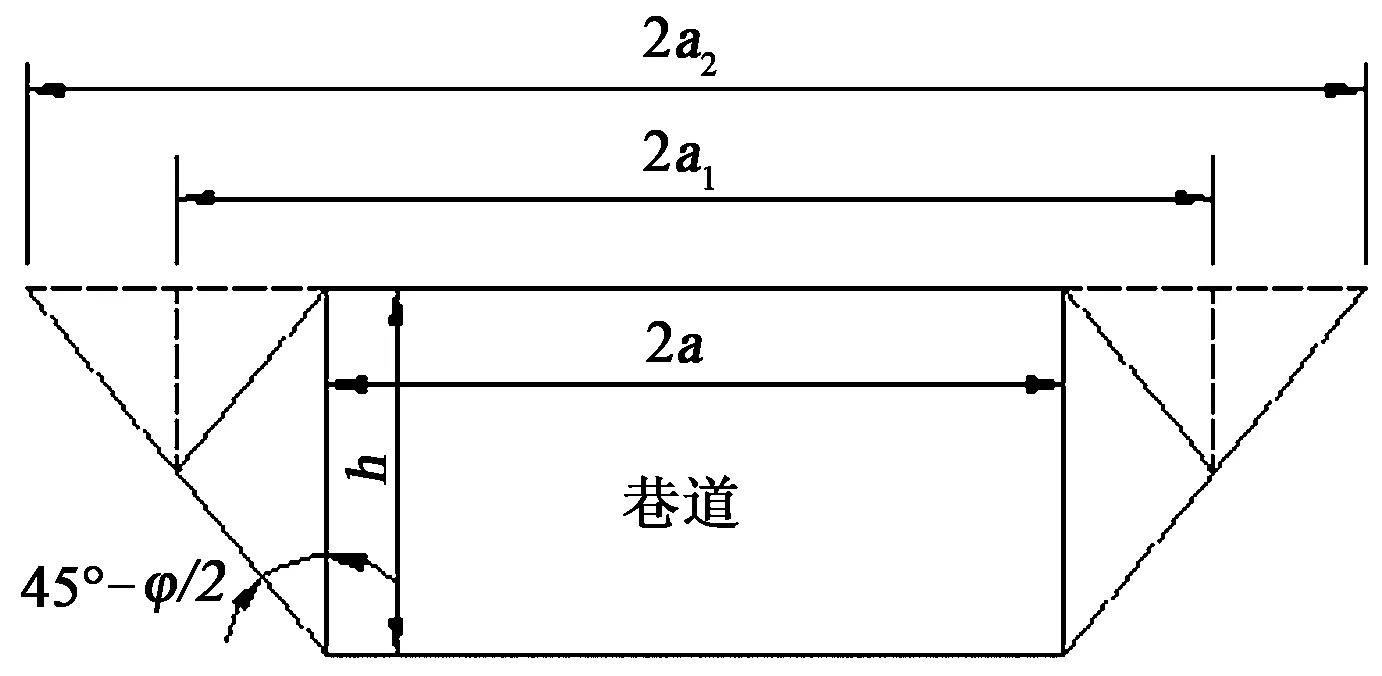
图8 不同平衡拱下的巷道有效跨度

由图8可得层状顶板隐形平衡拱和扩展隐形平衡拱的巷道有效跨度[12-13]为：

(30)

式中，a为巷道半宽，m；a1为隐形平衡拱半跨度，m；a2为扩展隐形平衡拱半跨度，m；h为巷道高度，m。

得到巷道有效跨度的基础上，基于上述分析过程可得在垂直地层荷载和水平构造应力联合作用下层状顶板的隐形平衡拱和扩展隐形平衡拱形态及矢高，通过公式(28)进而可得支护设计时锚索的长度。限于篇幅，在此不再赘述。

4 结 论

通过分析普氏平衡拱理论对于层状顶板变形研究存在的不足，考虑巷道两帮稳定状态与平衡拱形态及矢高的关系，对上覆地层压力和水平构造应力共同作用下露井联采中井工矿巷道层状顶板变形破坏后的平衡拱形态及矢高进行深入研究，考虑到理论计算与实际有一定区别，下一步将结合实际开展相关研究，该论文成果只是理论分析。

主要结论有：

(1)露井联采中井工矿巷道层状顶板岩体在垂直地层荷载和水平构造应力的综合作用下发生挠曲变形后将不断冒落而形成初始平衡拱。若不及时支护，层状顶板的初始平衡拱不断脱落，直至冒落成高形态极限自然平衡拱。

(2)露井联采中井工矿巷道层状顶板的平衡拱矢高与水平侧压力和巷道跨度密切相关。当λ<1时，地应力起主要作用，层状顶板上部一定范围内岩层在垂直地层荷载下出现较大塑性破坏范围，形成竖直方向的椭圆状平衡拱；相反，当λ>1时，水平构造应力起主要作用，层状顶板上部一定范围内的岩层在垂直地层荷载下出现较小塑性破坏范围，形成水平方向的椭圆状平衡拱。

(3)当巷道帮部为较软弱的岩体时，帮部易发生失稳，层状顶板自然平衡拱将进一步演变为隐形平衡拱和扩展隐形平衡拱。在得到巷道有效跨度的基础上，可分析在垂直地层荷载和水平构造应力联合作用下层状顶板的隐形平衡拱和扩展隐形平衡拱的形态及矢高，进而可得支护设计时锚索的长度。