中国混频金融状况指数的经济增长预测效果与检验
刘金全,张 龙
(吉林大学 a.数量经济研究中心;b.商学院,吉林 长春 130012)
一、引言
随着利率市场化、汇率市场化改革与中国金融业对外开放程度的不断深化与提高,金融冲击对实体经济的影响日益凸显,实体经济与金融市场之间的联系愈加紧密。一国的金融市场状况直接影响该国的宏观经济运行,金融稳定与经济增长是政策制定者的主要关注目标。宏观经济在内、外部冲击下,通过金融市场传导,呈现出一些持续性波动和周期性特征,金融稳定更是关系经济能否持续健康发展的重要因素。全球金融危机的爆发与蔓延,令各国政府清晰地认识到实体经济与金融市场之间的密切联系,而金融发展中的流动性“错位”可能带来“滞胀”等问题,给国家宏观经济调控带来了新挑战。新常态下,中国经济复杂多变,金融市场波动加剧,金融市场状况在经济形势评估中的作用愈加凸显。同时,地区金融发展与贫困减缓之间存在着明显的相关关系,正确认识二者之间的相关关系对中国金融精准扶贫工作的顺利开展具有一定参考作用[1]。在此背景下,构建反映金融市场波动、预测未来经济运行相对有效的动态金融状况指数,对于分析中国金融市场波动的典型特征、政府前瞻性地制定金融改革措施和宏观经济调整政策,意义重大。
金融状况指数(FCI)是涵盖调控金融市场的主要指标,便于政府判定金融市场稳定程度、把握宏观经济态势和评估经济政策效果,国内外学者对与之相关的问题展开了大量理论探讨与实证研究。
国外学者关于金融状况指数的研究,起源于20世纪80年代末加拿大银行提出的货币状况指数(MCI) 概念,大致经历了使用常系数模型构建静态FCI到使用时变系数构建动态FCI的演进过程。Freedman根据加拿大的金融运行状况,设计和测度了加拿大的MCI[2];随后,Ball基于利率和汇率指标,运用MCI考察了小型开放模型下的最优货币政策[3];Goodhart等进一步对MCI进行了金融变量拓展,基于利率、汇率、房价和股价通过总需求方程缩减式和VAR脉冲响应构建了7个主要发达经济体的FCI,并验证了FCI与CPI的领先滞后关系[4]。此后,关于FCI的研究主要集中在增加金融变量和使用动态权重方向上。Van den End在FCI基础上引入了金融机构偿付缓冲指数构建金融稳定状态指数(FSCI),开创了运用FSCI度量金融稳定状况的先河[5]。近期研究则集中在使用时变系数随机方差向量自回归(TVP-SV-VAR)模型、动态因子模型构建FCI,且在此基础上尝试对金融变量进行数量和维度上的扩展,如Matheson的有关研究[6];少数学者使用时变参数因子扩展向量自回归(TVP-FAVAR)模型测算的动态FCI对金融市场波动进行研究,如Koop等的有关研究[7]。
相比而言,国内对FCI的研究较晚,研究体系还不够成熟,选取合成FCI的金融指标大都参照国外已有模式。从研究方法上看,多数学者基于VAR模型、总需求方程缩减式、大型宏观经济计量模型等静态方法确定金融变量的权重,通过选取利率、汇率、股票价格、房地产价格、货币供应量等变量合成FCI,并分析FCI与经济增长、CPI之间的相关性及其预测能力,代表性学者有周德才等[8];针对上述研究方法,一些学者提出异议,具体认为VAR模型的变量排序存在一定主观性、总需求方程缩减形式要求金融变量相互外生、大型宏观经济模型的数据获取存在一定难度等诸多问题,提倡使用S-VAR、时变状态空间模型、VECM模型、TVP-FAVAR模型等动态方法确定各个金融变量的权重,分析FCI在不同区制、不同边界对经济增长和通货膨胀的预测,并尝试对新常态下的金融市场波动周期性特征进行动态解析,如邓创等的有关研究[9];个别学者采用了混频数据对中国FCI进行了动态研究,栾惠德等基于房价、货币供应量和社会融资规模等变量,并利用混频数据测算了中国的实时FCI,发现混频金融状况指数(MF-FCI)能够解释近年来中国货币政策的松紧程度,对经济增长和通货膨胀的预测效果较好[10];尚玉皇等基于国内生产总值(季度数据)与金融变量(月度数据)构建了一种MF-FCI模型,并运用MF-FCI模型对中国宏观经济进行了预测,认为MF-FCI的宏观经济预测效果优于同频FCI[11]。
梳理已有文献发现,国内外关于FCI的相关研究成果已经较为丰富,大量学者采用科学的动态方法测算了反映金融市场波动状况的FCI。动态方法克服了静态方法约束条件苛刻的问题,且考虑了参数权重的时变性特征,但受金融变量数据频率的制约,所构建模型的样本数据仍以加总或插值后的同频数据为主,而加总或插值法会导致信息损失和虚增,且构建的FCI只能依照金融变量可得的低频数据(年度、季度),而利率、汇率、房价和股价等数据均为高频数据(月度、日度),在构建模型时只能被迫转化为低频数据;低频数据的运用减少了样本容量,且不可避免地造成了信息损失,降低了数据样本信息和模型估计的有效性,导致预测精度的偏差,这在一定程度上使FCI丧失了部分金融市场流动性指示器的功能作用。然而,金融市场波动既不是一蹴而就,也不会持续变动,更多的是时断时续,具有一定随机性。鉴于此,本文综合前人的研究成果,运用TVP-FAVAR模型及其修订式测算中国FCI,比较同频与混频数据下FCI对经济增长的冲击效应及预测效果,并进一步通过MF-VAR模型检验SF-FCI和MF-FCI经济增长预测效果,以期为政府实现金融市场稳定和经济合理增长提供一定依据。
二、模型构建
金融市场发展与实体经济关系密切,科学测算FCI对稳定金融市场、保障经济持续增长意义重大。鉴于研究需要,本文构建TVP-FAVAR模型和MF-VAR模型,具体模型构建如下:
(一)TVP-FAVAR模型
FCI能够刻画金融市场整体的变动趋势,并对产出水平与通胀压力等有一定先导作用,为了追踪金融市场的波动态势,通常使用时变模型测算FCI:
(1)
(2)
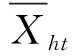
FCI的正负反映了一国的金融市场状况,一般将FCI均值定为基准0线,正值和负值分别表示金融市场状况向好和趋差。本文使用TVP-FAVAR模型对FCI的动态权重进行估计,VAR模型的估计原理是采用模型中各变量的滞后期值对其当期值进行回归,标准的VAR模型为:
yt=ρ1yt-1+ρ2yt-2+…+ρpyt-p+μt
(3)
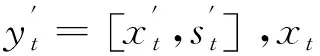
VAR模型对自由度的消耗使得一些金融变量很难通过有限变量完整地被呈现,而能够从大量数据集中抽取信息则成为VAR模型的改进方向。FAVAR模型假设经济中大量可观测序列的相互变化可由少数因子捕捉,将N维的可观测变量降解为K维的不可观测的因子向量,观测向量、因子与金融变量间的关联机制通过带有漂移项的随机游走进行刻画,具体形式如下:
(4)
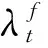
FAVAR模型解决了VAR模型由于自由度受限而导致信息量不足的问题,但对经济变量异常值敏感性的降低使FAVAR模型很难捕捉系统中各参数的时变特征,为了使模型结果更加可靠,本文参考Koop和Korobilis[7]的做法,构建TVP-FAVAR模型:
yt=ρ1tyt-1+ρ2tyt-2+…+ρp tyt-p+μt
(5)
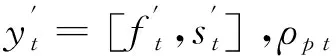
(6)
鉴于TVP-FAVAR模型的参数矩阵带有漂移变量,修正式(4)与式(5)得:
(7)
(8)
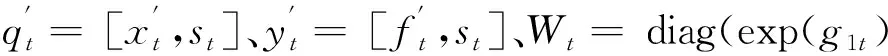
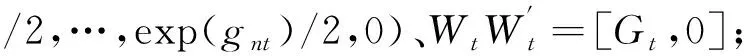
qt=λtρ1tyt-1+λtρ2tyt-2+…+λtρp typ-2+ϖt
(9)
(10)
TVP-FAVAR模型有效避免了VAR模型容易遗失信息的问题,且系数矩阵和扰动项协方差矩阵具有时变性。考虑本文主要研究经济增长率与FCI之间的关系,经济增长率为季度数据,合成FCI的金融变量为月度数据,式(2)中经济增长率受金融变量冲击时,同频模型的脉冲响应难以实现。
(二)MF-VAR模型
传统的Granger因果检验不可避免地会遇到数据频率不一致的问题,以往的处理方法是将高频数据通过加总或插值的方法将高频数据处理为低频数据,这种处理方法可能产生虚假Granger因果关系。鉴于此,本文参考刘汉等的研究[12],将混频技术和Granger因果检验结合起来,检验SF-FCI、MF-FCI与经济增长之间的因果关系。
首先对MF-VAR模型中的混频数据变量进行设定和说明,采用xh(ϑ,k)表示高频变量,xl(ϑ)表示低频变量,两者之间的比率为m;MF-VAR模型的主要做法是将可观测过程堆积为混频向量,在一个双变量混频数据模型中,一个高频变量和一个低频数据堆积成(m+1)×T的混频矩阵X(ϑ)=[xh(ϑ,1)′,xh(ϑ,2)′,…,xh(ϑ,m)′,xl(ϑ)′] ,如果低频数据为季度数据,高频数据为月度数据,则具体为X(ϑ)=[xh(ϑ,1)′,xh(ϑ,2)′,xh(ϑ,3)′,xl(ϑ)′] ,假定该堆积的混频数据服从MF-VAR(p)过程,则有:
(11)
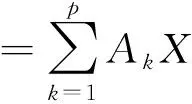
(12)
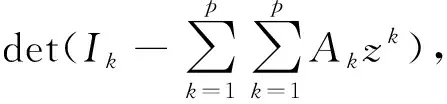
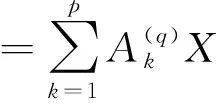
(13)
H0(q):RvecB(q)=r
(14)
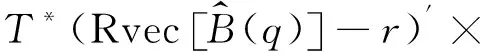
(15)
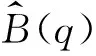
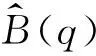
(16)
式(16)中PN(WT*)≤α表示在置信水平α下原假设不成立。当样本量较小时,通过自举的方法获得混频Granger因果检验的Wald统计量和P值。
三、理论推演与实证检验
(一)金融状况指数经济增长效应理论推演
运用FCI分析宏观经济问题,要求合成FCI的金融变量可以通过一定传导渠道对宏观经济产生影响。本文以扩张性货币政策为例,对合成FCI的各金融变量传导渠道进行理论推演。
1.利率传导渠道。随着中国利率市场化改革的逐步深入,以泰勒规则及其衍生形式为主的货币政策通过利率传导渠道对金融市场产生影响。具体而言,当中央银行实行扩张性的货币政策,而扩张性货币政策会导致实际利率水平下降,并带来企业筹资成本降低,引发企业投资支出增加,进一步影响总产出,利率传导渠道概括为“扩张性货币政策→利率下降→企业融资成本降低→投资支出增加→总产出增加”。
2.汇率传导渠道。货币主义学派认为汇率等资产的相对价格通过货币政策对实体经济产生影响,而资本账户开放和汇率市场化的逐步加深会使货币政策的汇率传导渠道更加畅通。具体而言,当中央银行实行扩张性的货币政策,而扩张性货币政策会导致实际利率水平下降、本币资产吸引力下降,带来本币汇率降低,引发净出口增加,进一步影响总产出,汇率传导渠道概括为“扩张性货币政策→利率下降→汇率下降→净出口增加→总产出增加”。张辉等基于货币政策和汇率传导模型,通过实证方法验证了中国货币政策的汇率传导机制各环节的有效性,并详细论述了市场和非市场条件下的传导机制[13]。
3.资产价格传导渠道。根据托宾q理论和财富效应理论,货币政策可以通过资产价格对投资和消费产生影响,进而影响总需求。具体而言,当中央银行实行扩张性的货币政策,居民实际货币持有量多于意愿货币持有量,居民用于购买生利资产(如股票)的货币支出增加,带来资产价格上升,托宾q值变大,引发投资支出增加,进一步影响总产出;同时,由于财富效应,当股票价格上升会带来金融财富价值上升,公众可利用资源增加,导致消费支出增加,进一步影响总产出。总之,货币政策通过影响资产价格,经“托宾q效应”和“财富效应”影响投资支出和消费支出,从而引起总需求变化。资产价格传导渠道可概括为:“扩张性货币政策→资产价格上升→托宾q增加/金融财富增加→投资/消费增加→产出增加”[注]利率和汇率实际可以看成资产价格,通过资产价格传导渠道进行分析,由于利率、汇率的传导渠道研究较为成熟;本文单独推演,文中资产价格传导主要指股票价格传导、房地产价格传导。。贾庆英等以房地产为代表,运用PVAR模型分析了资产价格对价格传导的影响,得出房价具有一定经济杠杆作用[14]。
4.信贷传导渠道。信贷传导渠道理论认为,由于信贷市场存在信息不对称现象,货币政策通过资产负债表和银行信贷等渠道影响企业投资和消费,从而对产出产生影响。具体而言,当中央银行实行扩张性的货币政策,而扩张性货币政策会导致银行准备金和存款增加,并带来引发银行可借贷资金增加,引发企业投资支出(或消费支出)增加,进一步影响总产出,信贷传导渠道概括为“扩张性货币政策→银行可借贷资金增加→投资/消费支出增加→产出增加”。姚余栋等利用中国短期融资融券和短期货款所构建的金融市场总量融资结构数据进行了计量分析,表明中国确实存在信贷传导渠道[15]。
需要说明的是,上述分析是基于单一传导渠道的分析,实际上金融变量有时会发生交互、联合传导,如汇率传导渠道中的利率效用。刘金全等运用DSGE模型分析“名义利率调整、资产价值修复、实体经济复苏”传导渠道的有效性,得出名义利率调整可以带来资产价值修复,进而带动实体经济复苏[16]。同时,就中国金融市场而言,房价指数是构建FCI的重要影响因素,郭娜等通过SVAR模型分析了中国房价和利率间关系,发现房价冲击对利率政策具有显著正向影响,进而对实体经济产生影响[17]。本文通过对货币政策的利率、汇率等传导渠道的分析,并参考已有相关文献,基于利率、汇率和房价等金融变量而合成中国的FCI。
(二)中国金融状况指数的经济增长预测与检验
1.中国金融状况指数的经济增长预测分析。本文借鉴Goodhart等的研究[4],构建包含利率、汇率等变量的FCI,样本区间为1996年1月至2017年9月,数据来源于中经网统计数据库和国际清算银行。在构建模型之前,需对各金融变量数据进行季节调整、HP滤波等处理[注]考虑到金融变量在数据类型和计量单位存在差异,为了避免不同缺口值在量纲上的差异,且使回归系数及变量权重具有可比性,需对缺口序列进行标准化处理,使其在技术上具有可比性和可加性。,具体处理如下:第一,利用银行间7天同业拆借利率消除通货膨胀得到实际利率,使用X12法季节调整、HP滤波计算实际利率缺口,记为R_GAP;第二,利用反映多边汇率的实际有效汇率指数取自然对数并经X12法季节调整、HP滤波法计算实际汇率缺口,记为EX_GAP;第三,利用上证综合指数与深圳成指月度加权平均交易量消除通货膨胀得到实际股价指数,取自然对数后使用X12法季节调整、HP滤波计算实际股价缺口,记为ST_GAP;第四,利用公式(国房景气指数-100)/100计算实际房价缺口,记为HA_GAP;第五,利用广义货币供给量M2消除通货膨胀得到实际货币供给量,取自然对数后使用X12法季节调整、HP滤波计算实际货币缺口,记为M2_GAP;第六,利用金融机构各项贷款月末数据消除通货膨胀、取自然对数后经X12法、HP滤波法计算实际信贷缺口,记为LD_GAP。
同时,本文采用ADF检验和PP检验对处理后金融变量数据的平稳性进行检验,具体平稳性检验结果见表1。
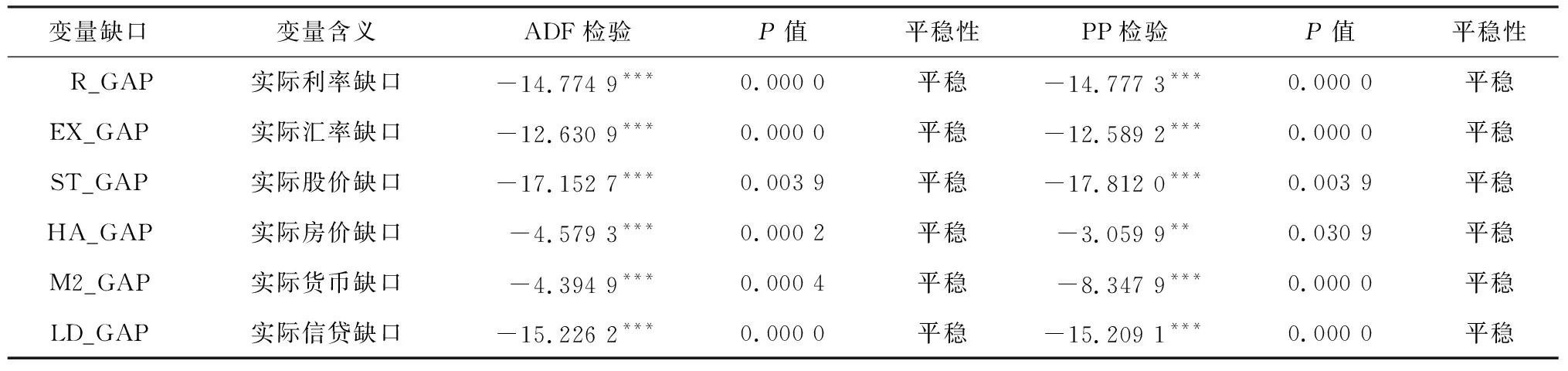
表1 金融变量单位根检验结果表
注:***、**表示在1%、5%的水平下显著;表中金融变量缺口反映货币市场、 资本市场、 房地产市场等比变动情况。
由表1可知,多数金融变量在1%的水平上拒绝存在单位根的假设,个别变量(HA_GAP的PP检验)在5%的水平上拒绝存在单位根的假设,说明金融变量数据为平稳时间序列,可以构建模型。直观观察合成FCI的各金融变量的时点、时序特征,有利于分析中国金融市场的变迁与波动态势,利用相关数据描绘合成FCI的各金融变量缺口,如图1所示。
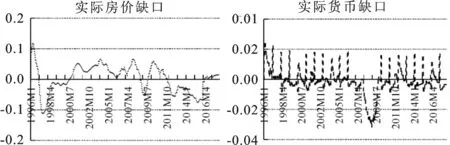
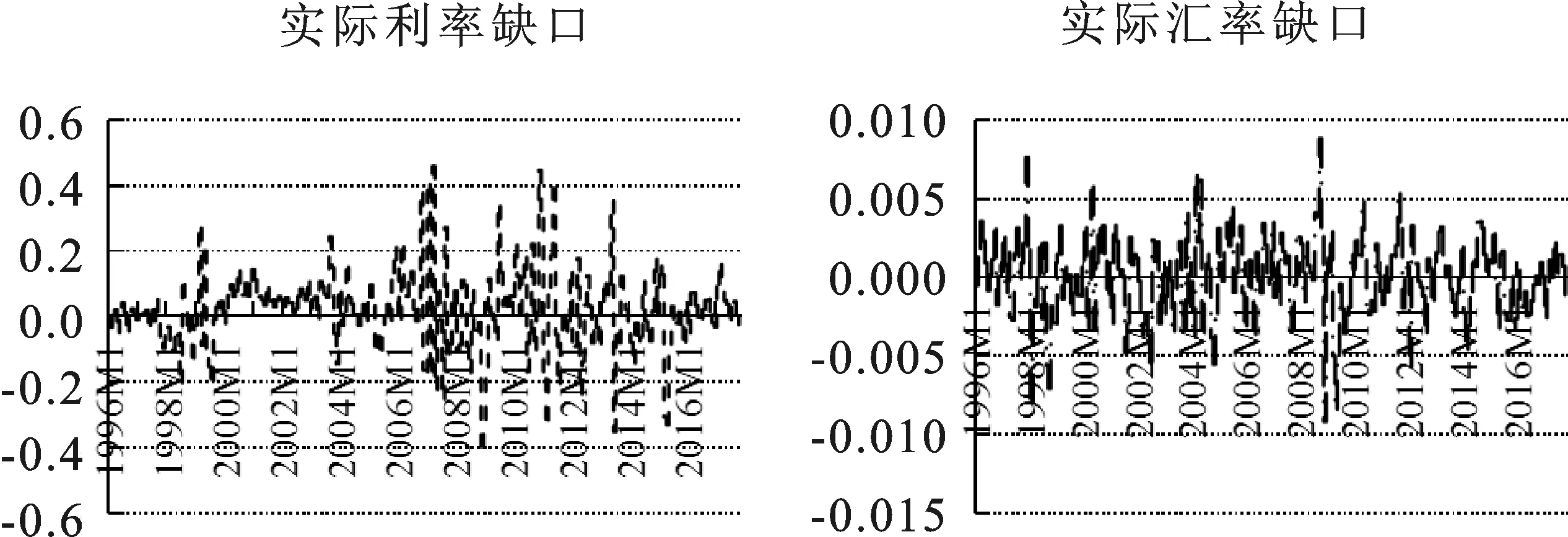

图1 合成FCI的各金融变量缺口图
从合成FCI各金融变量缺口的波动状况看,各金融变量的缺口波动幅度、走势等存在较大差异。横向看,同一金融变量在不同时点差距较大,具有一定政策分布性;纵向看,不同金融变量在同一时期差异较为明显,波峰、波谷分布及落差不尽相同,说明单一金融变量难以反映整个金融市场的发展态势。同时,金融变量月度数据波动的频繁性也说明将各金融变量的高频数据变换为低频数据,进而测算FCI的权重可能造成信息遗漏,可能存在偏差。
为了验证低频数据向高频数据转换简单平均做法的不合理,本文通过选取月度数据代表季度数据的做法进行横向对比分析。具体而言,选取1月份数据代表1季度数据、4月份数据代表2季度数据、7月份数据代表3季度数据、10月份数据代表4季度数据,由“1-4-7-10”月度数据组成新的季度数据,记为序列1;类似地选取“2-5-8-11”月度数据组成新的季度数据,记为序列2;选取“3-6-9-12”月度数据组成新的季度数据,记为序列3[注]类季度数据的选择有81种方案,本文选择其中一种序列构建方式予以说明,其他方案并未一一列举。此外,对于各金融变量的动态权重及其政策导向原因,并非本文研究重点,故并未做具体分析。。运用Matlab2017a软件通过TVP-FAVAR模型测算序列1、序列2、序列3的动态FCI,分别记为FCI1、FCI2、FCI3,脉冲冲击周期定为8期,为了形成完整对比,研究区间选为1996年1月至2016年12月,3个序列的FCI具体走势见图2。
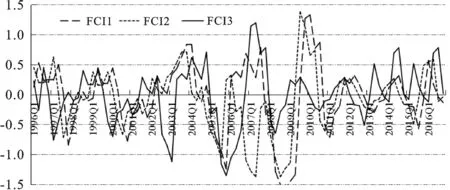
图2 中国FCI1、FCI2、FCI3走势图
观察图2可知,FCI1、FCI2、FCI3整体波动趋势大体相同,但FCI1、FCI2、FCI3的波峰、波谷位置存在差异性,且升降的起点、终点位置存在先后性,说明简单的数据频率转换存在一定误差,引入混频估计极为必要。为了说明FCI对于经济增长的预测功效及MF-FCI与SF-FCI的经济增长的预测优劣,本文运用TVP-FAVAR模型及其修订式测算中国SF-FCI和MF-FCI,并与经济增长率(GDPR)进行比较,SF-FCI、MF-FCI与经济增长的关系见图3。
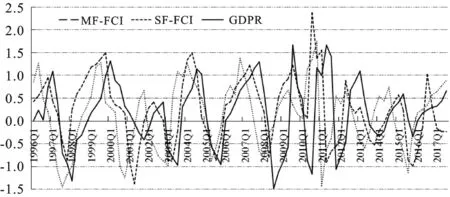
图3 中国SF-FCI、MF-FCI与经济增长关系图
观察图3可知,SF-FCI、MF-FCI的走势总体一致,且二者对于经济增长均具有一定先导性,但MF-FCI对于经济增长的预测效果更好。具体而言,从图3中的SF-FCI、MF-FCI与经济增长率的波峰和峰谷看,SF-FCI领先经济增长率大约1~2季度,拟合效果较好;MF-FCI显著领先经济增长率大约2~4个季度,拟合效果很好,二者对“次贷危机”、“欧债危机”等事件均具有一定预测性,说明SF-FCI和MF-FCI对于经济增长均具有一定先导性,但SF-FCI、MF-FCI对于2003年1季度的经济增长率低点均未有合理预测,而造成经济增长率下降的主要原因为SARS的爆发,属于不确定事件。
需要说明的是,“新常态”时期以来SF-FCI与经济增长率的走势出现较大背离,预测功效受到严重考验,MF-FCI的经济增长先导效果虽然也有所减弱,但总体预测功效仍然较好,分析其原因可能是,新常态下,中国金融市场更加复杂化,加之金融市场变量瞬息万变,传统同频处理方式造成的部分信息遗漏可能对预测功效产生较大影响。
2.中国金融状况指数的宏观经济效应分析。由图2可知SF-FCI和MF-FCI可能具有一定的经济增长效应,且MF-FCI的先导作用更加显著,为了进一步验证SF-FCI和MF-FCI的经济增长效应,本文通过带有随机波动率的TVP-FAVAR模型[注]带有随机波动率的TVP-FAVAR模型记为SV-TVP-FAVAR模型,此处不做详细介绍。,对SF-FCI和MF-FCI的经济增长效应展开三维脉冲响应分析。
1)变量选取与共同因子提取。SV-TVP-FAVAR模型所需数据来源于中经网统计数据库,为了有效避免经济系统的信息遗漏问题,本文选取46个相关变量提取共同因子,其中总量型变量需经CensusX12法季节调整和GDP平减等处理;指数型变量需转化为增长率数据,并进行标准化处理;剔除量纲影响,进行共同因子提取,共同因子序列需进行单位根检验,结果显示共同因子在1%的显著性水平上拒绝存在单位根,数据平稳。进一步以GDP增长率和CPI增长率为产出和通货膨胀的代理变量,发现共同因子与经济基本面变量波动转折点前后GDP和CPI的趋势性走势符合中国宏观经济既定发展事实。
2)产出对SF-FCI和MF-FCI冲击的脉冲响应分析。本文运用SV-TVP-FAVAR模型,检验1996年1季度至2017年3季度产出对SF-FCI和MF-FCI冲击的脉冲响应,SF-FCI和MF-FCI对产出增长率的冲击效应见图4(上图为SF-FCI,下图为MF-FCI)。
由图4可知正向的金融市场冲击主要引起产出增加,具体而言:
一是1个单位正向SF-FCI冲击主要引起产出的正向响应。从响应维度看,响应的持续期整体相对较长,响应期均值为8个季度,冲击发生后产出增长率的响应收敛性较好。从响应极值看:响应极大值发生在2009年2季度,响应值为0.09;响应极小值发生在1998年3季度,响应值为-0.04,最大响应差为0.13;冲击发生后产出增长率的冲击响应值有一定典型特征,主要体现在1998年前后的亚洲金融危机时期、2009年前后的全球金融危机时期和2015年前后的经济新常态时期。
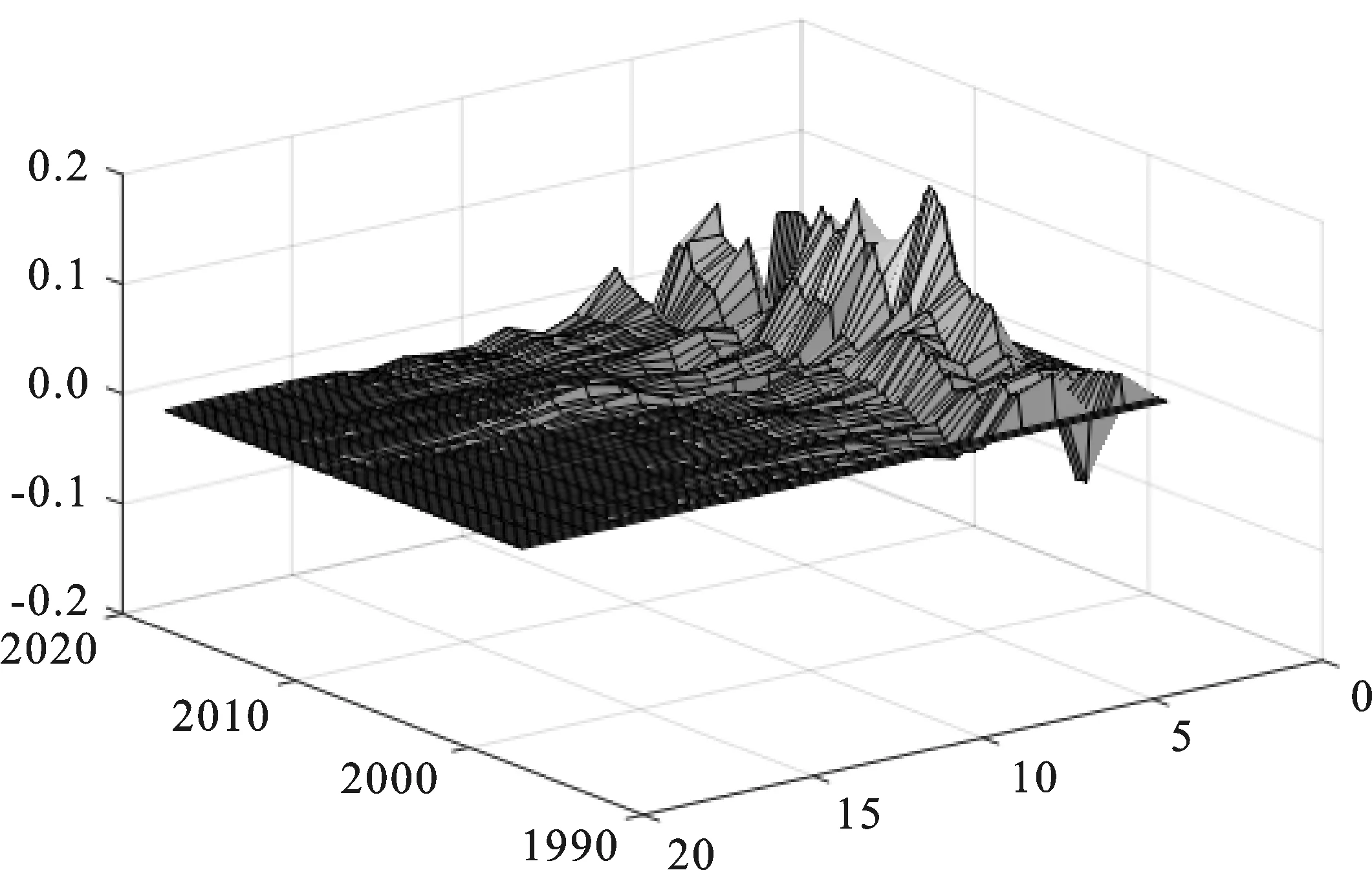
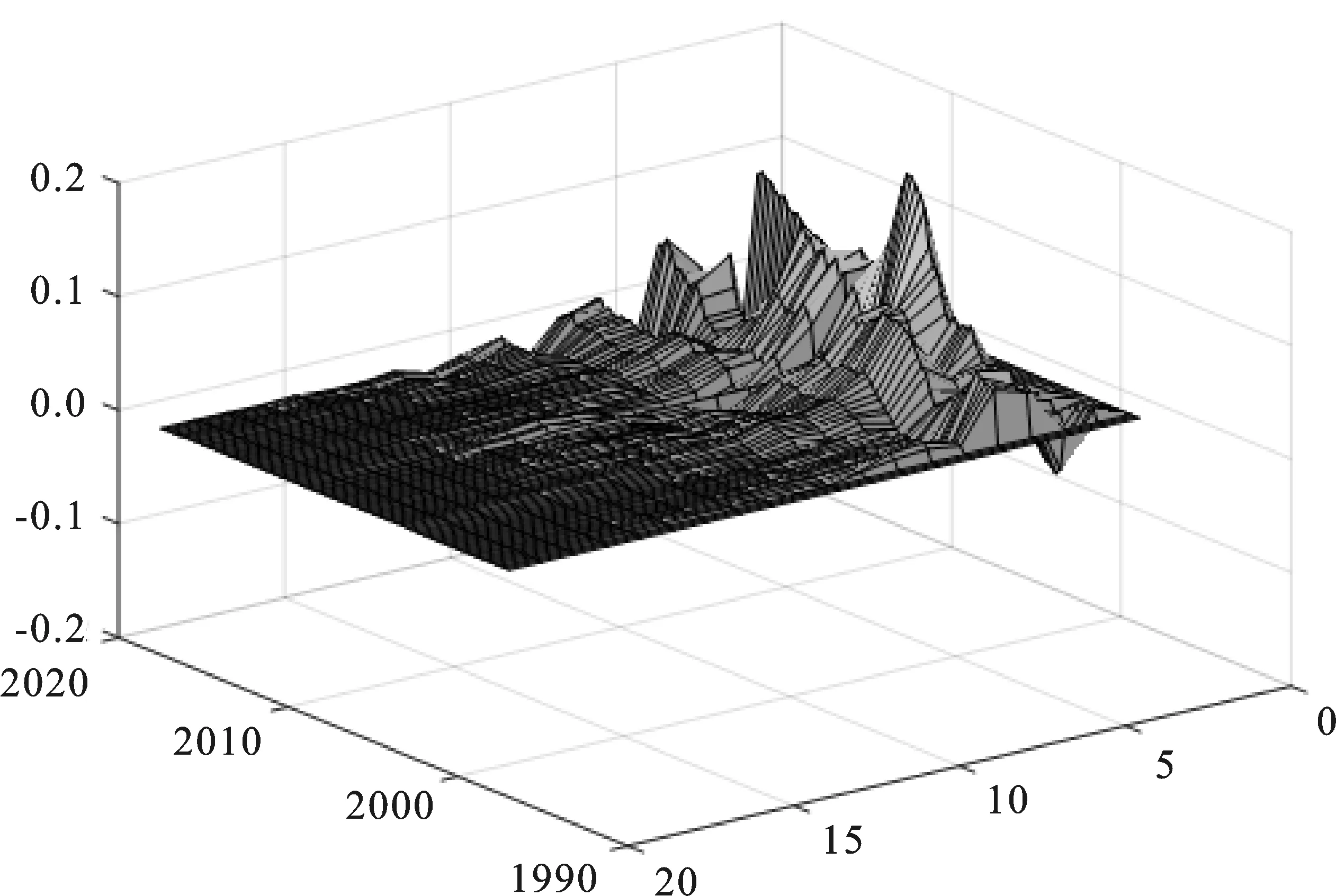
图4 SF-FCI和MF-FCI对产出的冲击图
二是1个单位正向MF-FCI冲击主要引起产出的正向响应。从响应维度看,响应的持续期较短,响应期均值为5个季度,冲击发生后产出增长率的响应收敛性较好。从响应极值看:响应极大值发生在2008年4季度,响应值为0.11;响应极小值发生在1997年4季度,响应值为-0.03,最大响应差为0.14;冲击发生后产出增长率的冲击响应值呈现出明显的周期性特征,主要体现在1998年前后的亚洲金融危机时期、2009年前后的全球金融危机时期和2015年前后的经济新常态时期。
综合SF-FCI和MF-FCI对产出增长率的冲击效应可知:产出增长率对SF-FCI和MF-FCI的脉冲响应维度一致,SF-FCI和MF-FCI的冲击基本不存在异质性,均能起到调控经济增长的作用;结合经济增长对SF-FCI和MF-FCI的冲击极值、响应周期、经济收敛性和冲击响应典型事件预测性等特征,MF-FCI在典型时期预测经济增长的先导性更强、正向冲击极值更大、负向冲击极值更小,而MF-FCI的经济增长效应更佳,且预测性更强。
3.中国金融状况指数与经济增长因果关系检验。本文通过混频Granger方法检验SF-FCI、MF-FCI与经济增长的因果关系,同时为了确定混频技术的优越性,对SF-FCI、MF-FCI和经济增长之间的因果关系进行Granger因果和混频Granger因果检验,具体结果见表2。
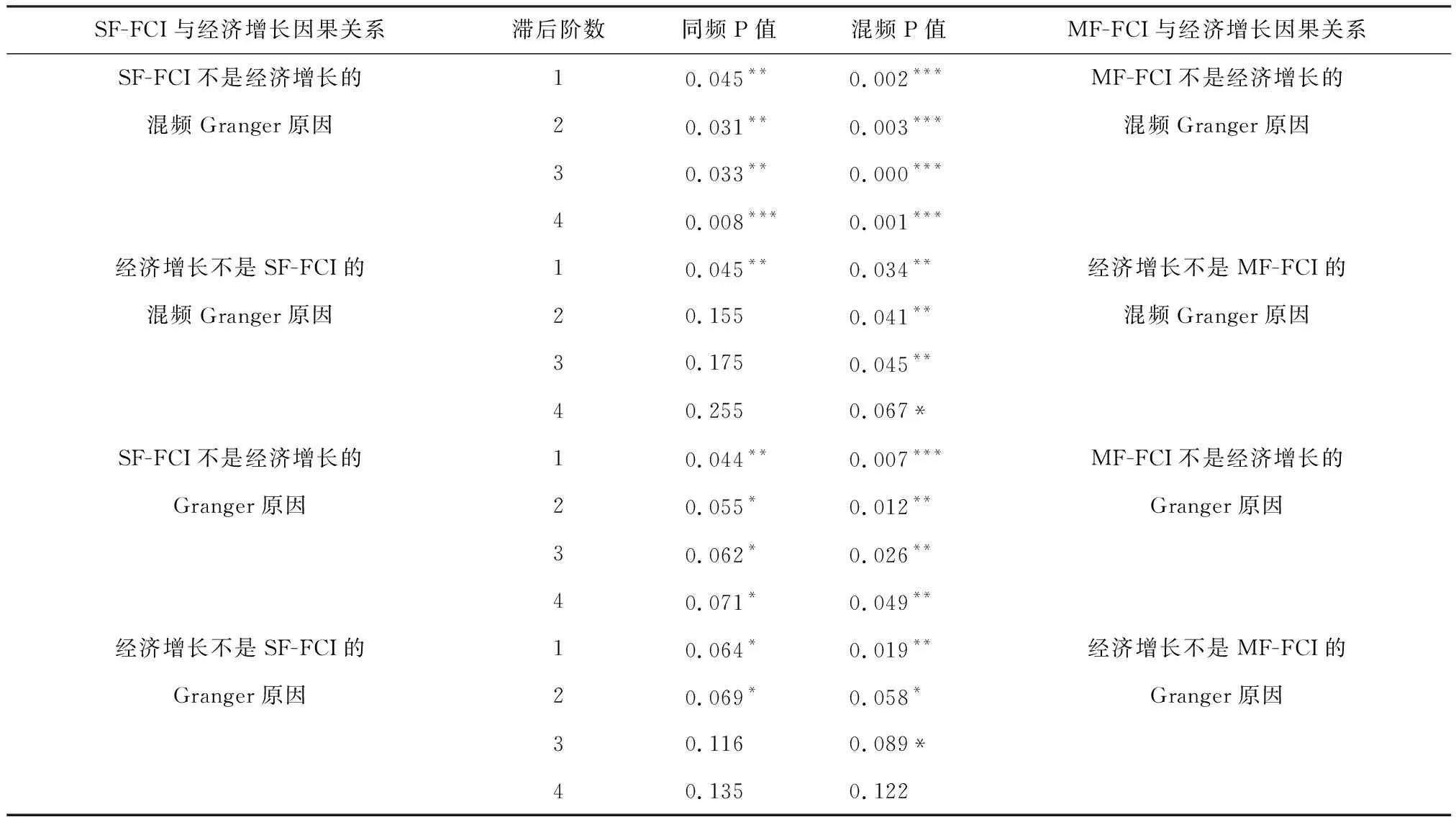
表2 SF-FCI、MF-FCI与经济增长的混频Granger因果检验表
注:***、**、*表示在1%、5%、10%的水平下显著;表中给出的SF-FCI、MF-FCI与经济增长的因果关系均为Granger因果检验和混频Granger因果检验的原假设。
从表2结果可看出,选择不同的滞后阶数,混频Granger因果和同频Granger因果检验结果存在较大差异,且Granger因果检验和混频Granger因果检验对于FCI与经济增长的因果关系有一定影响。
1)Granger因果检验。中国SF-FCI滞后1阶在5%的显著水平上拒绝原假设,表明SF-FCI是经济增长的Granger原因,滞后2~4阶在10%的显著水平上拒绝原假设,表明SF-FCI是经济增长的Granger原因;经济增长滞后1~2阶在10%的显著水平上拒绝原假设,表明经济增长是SF-FCI的Granger原因,滞后3~4阶在10%的显著水平上接受原假设,表明经济增长不是SF-FCI的Granger原因;中国MF-FCI滞后1阶在1%的显著水平上拒绝原假设,滞后2~4阶在5%的显著水平上拒绝原假设,表明MF-FCI是经济增长的Granger原因;经济增长滞后1阶在5%的显著水平上拒绝原假设,滞后2~3阶在10%的显著水平上拒绝原假设,表明经济增长是MF-FCI的Granger原因,滞后4阶在10%的显著水平上接受原假设,表明经济增长不是MF-FCI的Granger原因。通过对SF-FCI、MF-FCI与经济增长的Granger因果检验发现,MF-FCI是经济增长的Granger原因,SF-FCI基本认定是经济增长的Granger原因,二者可以用来预测经济增长的未来发展趋势,但MF-FCI与经济增长的因果关系比SF-FCI更密切。
2)混频Granger因果检验。中国SF-FCI滞后1~3阶在5%的显著水平上拒绝原假设,滞后4阶在1%的显著水平上拒绝原假设,表明SF-FCI是经济增长的混频Granger原因;经济增长滞后1阶在5%的显著水平上拒绝原假设,表明经济增长是SF-FCI的混频Granger原因,滞后2~4阶在10%的显著水平上接受原假设,表明经济增长不是SF-FCI的混频Granger原因;中国MF-FCI滞后1~4阶在1%的显著水平上拒绝原假设,表明MF-FCI是经济增长的混频Granger原因;经济增长滞后1~3阶在5%的显著水平上拒绝原假设,滞后4阶在10%的显著水平上拒绝原假设,表明经济增长是MF-FCI的混频Granger原因。通过对SF-FCI、MF-FCI与经济增长的混频Granger因果检验发现,MF-FCI和SF-FCI都是经济增长的混频Granger原因,二者可以用来预测经济增长的未来发展趋势,但MF-FCI与经济增长的因果关系比SF-FCI更密切。
综合来看,Granger因果检验和混频Granger因果检验均表明MF-FCI对于经济增长的预测效果更好,对比Granger因果检验和混频Granger因果检验对于MF-FCI与经济增长的检验发现,混频Granger因果检验揭示出的MF-FCI与经济增长的因果关系更密切,混频技术对于衡量FCI与经济增长之间的关系尤为必要。
四、结论
本文采用1996年1月至2017年9月的利率、汇率、股价等金融变量数据,利用TVP-FAVAR模型及修订式测算中国动态FCI,并基于SV-TVP-FAVAR模型比较MF-FCI和SF-FCI的经济增长效应,进一步运用混频Granger方法检验MF-FCI和SF-FCI的经济增长预测功效,得出主要结论如下:
第一,合成FCI的各金融变量缺口存在较大差异,FCI的混频估计比同频估计更合理。通过对各金融变量缺口及类季度数据FCI的比较分析可知,各金融变量的缺口波动幅度、走势等存在较大差异,同一金融变量在不同时点缺口数值差距较大,不同金融变量在同一时期缺口差异较为明显,波峰、波谷分布及落差不尽相同。在研究区间内,FCI1、FCI2、FCI3的趋势性特征存在一定差异,简单的同频转换存在一定误差,引入混频估计极为必要。
第二,MF-FCI比SF-FCI更适合中国,可作为经济增长的先行指标。SF-FCI、MF-FCI的走势总体一致,二者对于经济增长均具有一定预测性,但MF-FCI显著领先于经济增长率大约2~4个季度,SF-FCI领先于经济增长率大约1~2季度,MF-FCI对于经济增长的预测效果更好。“新常态”时期以来,SF-FCI和经济增长率的走势出现较大背离,预测功效受到严重考验;MF-MFI的经济增长先导效果虽然有所减弱,但总体预测功效仍然较好,MF-FCI在典型时期预测经济增长的先导性更强,正向冲击极值更大、负向冲击极值更小,MF-FCI的经济增长效应更加显著。
第三,MF-FCI与经济增长的因果关系比SF-FCI与经济增长的因果关系更密切。通过对SF-FCI、MF-FCI与经济增长进行Granger和混频Granger因果检验发现:MF-FCI是经济增长的Granger和混频Granger原因,经济增长是MF-FCI的Granger和混频Granger原因;SF-FCI是经济增长的Granger和混频Granger原因,经济增长不是SF-FCI的Granger和混频Granger原因;MF-FCI和SF-FCI均可以预测经济增长的未来发展趋势,但从显著性水平和滞后期显著性看,MF-FCI与经济增长的因果关系比SF-FCI更密切。
金融市场发展与实体经济关系密切,构建全面反映金融市场波动态势、预测短期经济运行的MF-FCI,对于政府前瞻性地制定宏观经济政策具有一定指导意义。

