高空作业车伸缩臂臂架截面优化
王余贤,高崇仁,孙 迪,殷玉枫
(太原科技大学 机械工程学院,太原 030024)
起重机的起重臂分为直臂式和混合式,是起重机作业时主要的受力构件,占起重机总重量百分比的20%~30%,大吨位起重机的幅度和起升高度受臂架自重的制约。因而,运用优化设计算法降低起重机臂架自重,对提升起重机整体性能有着很大的意义,也成为了起重机行业的竞争趋势。汽车起重机伸缩臂直臂式作为本文研究对象,选取QY50汽车起重机为研究对象。应用ansys软件对QY50U型臂架截面进行优化设计分析,降低起重机臂架自重,对提升起重机整体性能有着很大的意义。
1 有限元模型建立
随着起重机行业的发展,伸缩臂臂架的截面也在不断的优化,臂架也在不断地实现轻量化。起重机伸缩臂臂架发展过程中,典型截面形状代表有:四边形、梯形、六边形以及U形截面等。四边形截面臂架在中、小吨位汽车起重机中得到广泛的应用,但是这种四边形截面臂架在汽车起重机的承载能力方面不足,不能够充分发挥材料的性能;五边形截面具有上盖板宽,呈倒“V”形特点,此结构不仅改善了下盖板的局部稳定性能,而且材料的力学性能也能够得到较好的发挥。六边形是上、下盖板弯折形,受力合理,具有较高的抗屈服能力。U形截面臂架具有受力均匀的特点,不仅能够提高整体稳定性和抗屈服能力,而且材料的力学性能也得到了充分发挥,并且随着科学技术的持续发展,工业设备的生产能力大幅提高,U行截面的伸缩臂臂架的使用将会越来越广泛。
U型截面如图1:

图1 U型截面
Fig.1 U section
1.1 模型选择及简化
本文选取QY50典型的U形臂架为研究对象,基于有限元,运用ansys对汽车起重机伸缩臂臂架进行优化设计。为了建模方便,可以只考虑臂架内的液压缸的重量,归结为臂架的自重。对伸缩臂臂架影响较小的零部件或者加强筋忽略。简化后的零部件有:伸缩臂臂架和滑块。伸缩臂臂架的单元类型选择shell63单元,主要有三个原因。第一,当一个实体结构的厚度不大(相对于长宽尺寸)时,且弯曲作为其主要变形,可以用壳单元进行建模.第二,与实体单元相比,壳结构具有优化时间短,优化精度高的优点。第三,考虑到伸缩臂的实际情况,伸缩臂架模型上、下盖板的厚度由实际常数决定。因此盖板的单元类型选择为shel l63.由于滑块主要承受摩擦力和挤压应力,因而对滑块进行建模时,其单元类型为solid45.
1.2 约束处理
由于伸缩臂只相对于伸缩方向上的滑块滑动,伸缩臂的约束主要发生在基本臂的两端,转台的铰链和铰接的液压缸,因此两个方向的平移和三个方向的转动需要约束。通过节点耦合的方式解决臂架与滑块之间的耦合问题,比建立接触对的方式更加方便、快捷,计算结果更精确。[1]进行建模后,伸缩臂臂架的模型如图1所示:

图2 伸缩臂臂架模型图
Fig.2 Model of telescopic boom
2 载荷及工况确定
对臂架进行受力分析,在起升载荷的作用下,不仅会导致臂架弯曲,并且会导致起重机倾翻。伸缩臂臂架幅度的变化会导致两个分力大小的改变。起重机的起重量是随幅度变化而变化的:在小幅度时,臂架强度制约着起重机的起重量,超载可能导致臂架弯曲而不能正常工作,因而臂架的强度决定起重机正常工作时的起吊能力;大幅度时,起重机稳定性制约着起重机的起吊能力,在起重机失去稳定性时,会导致起重机倾翻。而钢丝绳强度的制约着起重机的最大起升载荷,而且超载会导致钢丝绳断裂。因而,对伸缩臂臂架进行优化设计时,只需考虑起重机在小幅度时的工况即可。伸缩臂臂架所受载荷有起升载荷、臂架自重、物品偏摆力、风载荷以及惯性载荷等。[2]
额定起升绳拉力Fs
(1)
式中:n是滑轮组倍率,η是滑轮组效率,η额定起升载荷。
在变幅平面内,沿臂架方向的轴向力
(2)
式中:θ-伸缩臂臂架在变幅平面内的倾斜角;
β-起升绳与臂架轴线的夹角;
Pab-臂架重力;
在变幅平面内,沿轴向的垂直力
(2)
在回转平面内,沿臂架轴线产生的轴向力
(4)
风载荷
PW=CPA
(5)
式中:C风力系数,P工作状态风压,取P=250 Pa,A臂架迎风面积由于汽车起重机在不同的条件下:臂架仰角和伸缩长度,能组合成不同种的工况。但本文只需考虑汽车起重机作业时的最不利状况,即伸缩臂臂架全伸,臂架仰角78,起重量8.5 t.对汽车起重机伸缩臂臂架进行强度、刚度和稳定性计算,最后利用ansys对汽车起重机伸缩臂臂架进行受力分析。[3]
3 伸缩臂静力分析
QY50汽车起重机伸缩臂臂架的质料为BS700钢板。额定最大起重量是50吨,其屈服极限σs=700 MPa,强度极限b=800 MPa,则钢板的许用应力为526 MPA.对已建模完成的模型进行加载以及求解分析,可以得到臂架在次工况下的等效应力图。如图3所示,可以看出伸缩臂最大应力出现在变幅液压缸支承铰点处,最大应力为270.294 Pa,最大静位移59.7789 mm.QY50汽车起重机伸缩臂在此工况下,满足强度和刚度需求,能够正常作业。但工作强度和刚度还有改善空间,因此可以对伸缩臂截面宽度和高度进行优化分析,降低臂架自重。

图 3臂架等效应力图
Fig.3 Equivalent stress diagram of boom

图4 最大局部放大图
Fig.4 Maximum local enlargement
4 伸缩臂截面优化
4.1 设计变量
设计变量就是在设计过程中不断地调整修正赋值的数据。就伸缩臂臂架来说,其长度是不能变更的,可改变的参数只有截面的材料以及宽B11度和高度H11.因此可以取伸缩臂臂架截面高度H11和宽度B11作为优化设计的变量。截面宽度B的设计变量有:B11、B21、B31和B41;截面高度H的设计变量有:H11、H21、H31和H41.
4.2 状态变量
状态变量是在满足设计变量参数下的因变量,是随着自变量的改变而改变,即是设计变量的函数。伸缩臂臂架能够正常工作的条件为满足应力和刚度,因此状态变量设置为伸缩臂臂架的应力和应变参数。即应力和应变满足:
0≤δmax≤[δ],0≤ιmax≤[ι].
4.3 目标函数
降低臂架自重作为伸缩臂臂架优化设计的主要目的,故将伸缩臂臂自重作为目标函数。在利用有限元模型进行求解分析时,应将伸缩臂总体积的最小值作为最优解。
V(X)=vmin(x)[4]
4.4 优化方法
在ANSYS分析软件中,提供了零阶方法和一阶方法,前者能够解决大多数优化问题,比较常用。后者基于目标函数对设计变量的分析程度,故非常适用于精确度高的优化分析。因此可以先将零阶方法和一阶方法结合使用,前者对模型进行快速优化求解。一介方法在前者优化序列不收敛时,在给定的约束范围内求得最优解。[5]
5 伸缩臂臂架优化结果
臂架截面高度H和截面宽度B与序列号之间的关系曲线图如图5、图6所示。从中可以看出:截面高度H和截面宽度B随着优化的次数增加,伸缩臂体积不断向最优值靠近。为了更清晰表达优化后的结果,列表列出了优化前后圆整后的截面数据如图表1:从表中我们可以得出优化后假面宽度B和截面高度H分别优化了30 mm和40 mm.臂架体积与序列号之间的关系曲线图如图7所示。从曲线中可以得到:在满足强度和刚度的双重约束条件下,第12次是臂架体积的最优解。
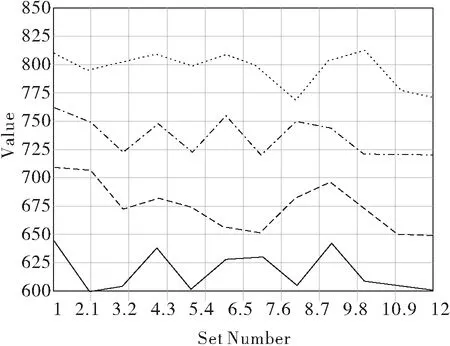
图5 截面H随序列号曲线图
Fig.5 Change chart of section H with sequence number

图6 截面B随序列号变化图
Fig.6 Change chart of section B with sequence number

图7 伸缩臂体积与序列号曲线图
Fig.7 Telescopic arm volume and serial number curve表1 伸缩臂臂架优化前后圆整后的参数
Tab.1 The parameters before and after optimization

/mm优化前优化后优化差值B1150047030B2155052030B3150047030B4145042030H1181077040H2176072040H3171067040H4164060040Dmax5998-39Smax270374-104
6 结论
QY50汽车起重机伸缩臂臂架建模时总体积0.60×109mm2,通过ansys优化后的总体积为0.57×109mm2,伸缩臂臂架优化前后的总体积减少了6%,与预期的结果相符。由此得出,通过运用ansys软件,对伸缩臂臂架进行优化设计是一种有效实用的方法。

