平行耦合带状线带通滤波器的分析方法

于正永，何晓凤，唐万春

(1.淮安信息职业技术学院 计算机与通信工程学院，江苏 淮安 223003；2.南京师范大学 物理科学与技术学院，江苏 南京 210023；3.淮阴工学院 电子信息工程学院，江苏 淮安 223001)

0 引言

滤波器作为一种无源器件，在微波集成电路系统和LTCC电路系统设计中被广泛应用[1-2]，其性能指标的好坏将直接影响整个电路系统的性能，平行耦合带状线带通滤波器[3]是较为常用的一种。目前对平行耦合带状线带通滤波器分析主要采用软件分析法[4-5]和传输线理论分析法[6]，其中传输线理论法将平行耦合带状线带通滤波器简单等效为多个带状线和多个平行耦合带状线的级联，但未考虑到该滤波器结构中开路线和阶梯跳变不连续性部分所带来的传输损耗，其分析结果不够准确。针对以上不足，本文依据已获得的带状线不连续性等效电路模型及其理论[7]，运用传输线基本理论推导出了附加开路线的平行耦合带状线的传输矩阵公式，将本文滤波器看作单根带状传输线、阶梯跳变和附加开路线的平行耦合带状线多个子网的级联，从而提出了一种平行耦合带状线带通滤波器的分析方法。

1 等效电路分析理论

平行耦合带状线带通滤波器通常是由多段耦合带状线级联而成，其结构中存在的开路线、阶梯跳变不连续性部分将产生一定的传输损耗，会直接影响到滤波器的性能，所以在分析该滤波器时应加以考虑。本文在已获得的带状线开路线不连续性等效电路模型及理论[7]基础上，将平行耦合带状线带通滤波器作为单根传输线、阶梯跳变、附加开路线的平行耦合带状线等多个子网的级联，很容易知道整个滤波器的ABCD传输矩阵等于上述各个子网的ABCD传输矩阵的乘积，再依据传输矩阵与散射矩阵之间的关系[8]，最终获得该滤波器的散射参数。其中，单根传输线子网的ABCD传输矩阵可以根据传输线基本理论计算得到[6]，阶梯跳变子网的ABCD传输矩阵可以根据文献[7]提出的不连续性等效电路模型计算获得，本文将重点推导附加开路线的平行耦合带状线子网的ABCD传输矩阵计算公式，在推导过程中将开路线不连续性部分传输损耗等效到耦合带状线中，以便较为准确地分析该滤波器的散射参数。

附加开路线的平行耦合带状线子网结构示意图如图1所示，是在传统平行耦合带状线的端口2、端口4上分别加载线长为Δz的开路线形成的。考虑到图1中开路线所带来的不连续性传输损耗，运用文献[7]中带状开路线的等效电路模型，得到了每个附加开路线的输入阻抗：

(1)

式中，C为图1中开路线的分布电容[9]，依据电容电感的对偶关系很容易得到图1中开路线的分布电感；Cexcess为开路线并联电容，是带状传输线的角频率。

图1 附加2个开路线的平行耦合带状线结构

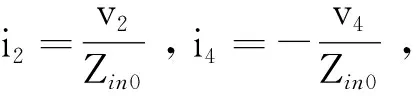
(2)

式中，

P11=P22=P33=P44=cosθ,

P12=P21=P34=P43=0,

式中，Z0e，Z0o分别表示侧边耦合带状线的偶模和奇模特性阻抗[11]；Y0e，Y0o为相应的偶模和奇模导纳；θ为带状传输线的电长度，对于带状传输线而言奇模电长度和偶模电长度是相等的。

2 算例验证与分析

为了验证本文等效电路分析方法的正确性和适用性，本文设计了一个平行耦合带状线带通滤波器，其结构示意图如图2所示。基本参数为：εr=2.2，h=2.0 mm，耦合带状线1和5：线宽W1=W5=0.19 mm，间隙S1=S5=0.176 mm，线长l1=l5=16.33 mm，耦合带状线2和4：线宽W2=W4=0.15 mm，间隙S2=S4=0.6 mm，l2=l4=16.19 mm，耦合带状线3：W3=0.215 mm，间隙S3=0.64 mm，线长l3=16.38 mm，输入输出端口处线长lp=10 mm，选取不连续性部分线长Δz=2 min(h1，h-h1)。

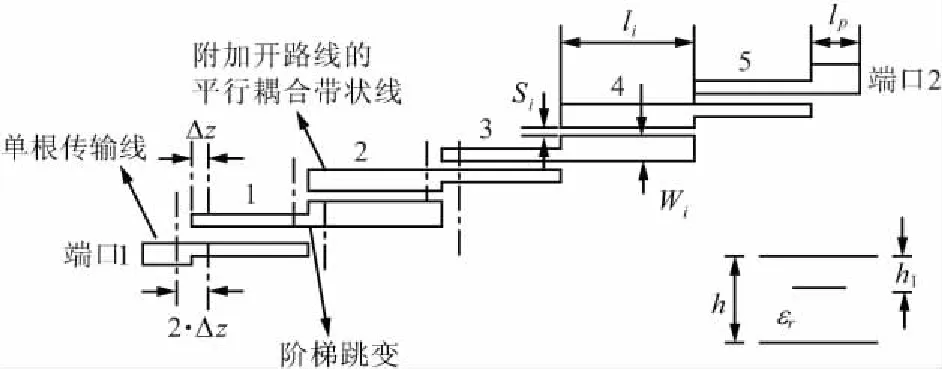
图2 平行耦合带状线带通滤波器结构

根据提出的等效电路分析理论，将图2所示滤波器等效成6个阶梯跳变子网(由2段长度均为Δz的不同宽度传输线连接而成)、5个附加双开路线的平行耦合带状线子网和输入输出端口处的2个单根传输线子网的级联。图3给出了在h1/h=0.1情况下，本文方法和仿真软件IE3D两种方法计算结果的对比曲线，其他h1/h取值情况也一样适用，这里不再给出。

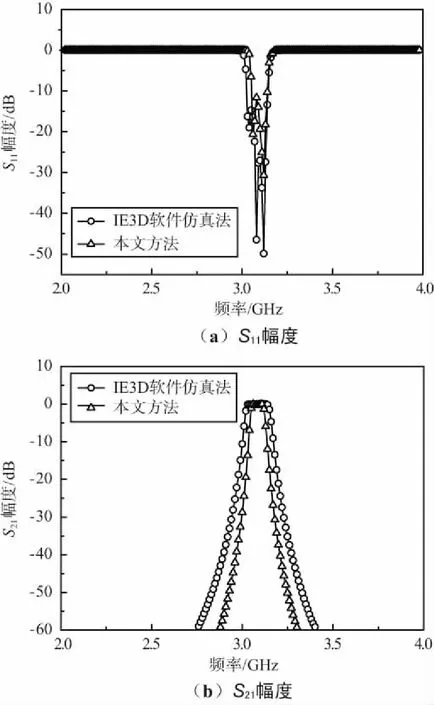
图3 平行耦合带状线带通滤波器的散射参数对比曲线

从图3可知，运用本文等效电路分析方法和IE3D软件仿真2种方法计算所得的滤波器S11幅度和S21幅度结果吻合良好，其平均误差小于2%。但也可以发现本文方法计算所得该滤波器的相对带宽较IE3D软件仿真结果有所变窄，主要原因是本文基于的带状开路线和阶梯跳变不连续性等效电路模型不够精确及相关公式的计算误差，后期可以通过文献[12]中的空间映射优化算法进一步优化和建模不连续性等效电路模型，从而确保更加准确地设计和分析此类微波电路器件。

3 结束语

在带状线不连续性等效电路模型基础上，推导出了附加开路线的平行耦合带状线传输矩阵的计算公式，通过将本文滤波器看作多个子网的级联，提出一种新颖的平行耦合带状线带通滤波器的等效电路分析方法，经验证得知，本文方法所得的计算结果与IE3D软件仿真结果吻合较好，且该滤波器散射参数的平均误差小于2%，为类似微波电路的设计和分析提供了借鉴。