传递矩阵法分析双层微穿孔管消声器的声学性能

王青，刘灿礼，陆静

(1.广西科技大学汽车与交通学院，广西柳州 545006；2.广西汽车零部件与整车技术重点实验室，广西柳州 545006)

0 引言

微穿孔吸声结构是马大猷教授提出并发展起来的新型共振吸声结构，具有良好的宽频消声效果，其吸声理论的正确性已得到学者们的验证，并且在声学控制中得到广泛应用[1-2]。微穿孔结构具有高声阻、低声抗、无多孔材料和无污染的优点，近年来逐渐用于消声器结构。微穿孔管消声器与穿孔管消声器具有相似消声原理，只是两者采用不同的穿孔声阻抗，因此，微穿孔消声器声学性能分析可以参考穿孔管消声器的计算方法。目前，微穿孔管消声器的研究通常采用微穿板理论和一维平面波理论，国内外学者们应用传递矩阵法对单层穿孔管消声器声学特性进行了理论计算，如程春等人[3-6]应用传递矩阵法对穿孔管消声器声学性能进行了分析。由于双层微穿孔结构具有更好的消声效果，双层微穿孔消声已逐渐用于工程实践，但双层穿孔管消声器声学特性的理论计算却鲜有文献介绍，且多局限于有限元法或实验研究[7]。因此，有必要提出双层微穿孔消声器声传递矩阵理论模型，对微穿孔管消声器进行参数化研究。本文作者基于平面波理论和微穿孔板吸声理论，推导了双层微穿孔消声器声传递矩阵控制方程，并结合时程精细积分进行计算。将理论计算结果与有限结果进行了对比，验证了方法的正确性，并分析了几何参数对双层微穿孔消声器声学性能的影响，该研究可为双层微穿孔消声器的研究提供新的思路和方法。

1 双层微穿孔消声器的声传递矩阵

图1为双层微穿孔消声器的声结构示意图，此消声器是由2层微穿孔管和膨胀腔组成。基于一维平面波理论，假设平面波在内、外层穿孔管和膨胀腔内传播，且声波在传播的过程中无机械能损耗。由连续性方程和运动方程[8]得到：

(1)

(2)

(3)

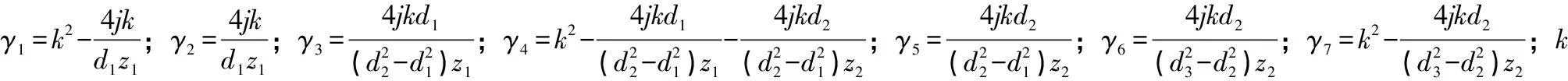
由运动方程得到内、外层穿孔管内和膨胀腔内声压与质点振速间的相互关系式为

(4)

(5)

(6)

式中：j2=-1；ρ为空气的密度；c为声速；u1、u2和u3分别为内、外层微穿孔管内的质点振速和膨胀腔内的质点振速。

图1 双层微穿孔消声器结构示意图

将式(4)—式(6)代入式(1)—式(3)，经整理后可得双层微穿孔消声器的一阶常微分矩阵控制方程：

(7)

根据精细积分法[9]，边界两端的传递关系可写成

W0=TW1

(8)

式中：W0为双层微穿管消声器的初始状态变量(x=0)；W1为消声器的终端状态变量(x=la)；T为传递矩阵，当系数矩阵A已知时，可精确计算传递矩阵T的值。

双层微穿孔管消声器膨胀腔两端与内插管形成一端开口一端闭口的直管，因此，在x=0和x=la处的膨胀腔内，有边界条件：

(9)

将式(9)代入式(8)中的后4式，经整理后可得

(10)

式中：H1=T41+Q1T31；H2=T42+Q1T32；H3=[T43+T44Q1]+Q1[T33+T34Q1]；H4=[T45+T46Q2]+Q1[T35+T36Q2]；H5=T61+Q2T51；H6=T62+Q2T52；H7=[T63+T64Q1]+Q2[T53+T54Q1]；H8=[T65+T66Q2]+Q2[T55+T56Q2]。其中，Q1=jtan(kla)；Q2=jtan(klb)，T11，......，T66为式(8)中传递矩阵T的元素。

由式(10)可得

p2(la)=N1p1(la)+N2u1(la)

p3(la)=N3p1(la)+N4u1(la)

(11)

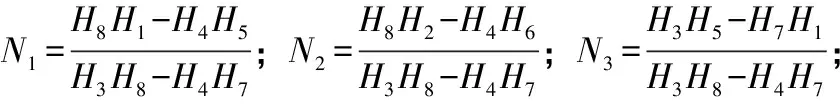
将式(9)和式(11)代入式(8)中的前2式可得

(12)

M11=T11+(T13+T14Q1)N1+(T15+T16Q2)N3

M12=T12+(T13+T14Q1)N2+(T15+T16Q2)N4

M21=T21+(T23+T24Q1)N1+(T25+T26Q2)N3M22=T22+(T23+

T24Q1)N2+(T25+T26Q2)N4

根据传递损失的定义，可得该消声器的传递损失[10]为

(13)

2 算例验证及声学性能分析

2.1 算例验证

在文中计算中，双层微穿孔管消声器的腔体长度l=80mm，扩张腔内径d3=50mm，内层穿孔管内径d1=20mm，外层穿孔管内径d2=30mm，穿孔管壁厚t=0.5mm，孔径dh=0.5mm，内插管长度l1=l2=10mm，穿孔率φ1=3%、φ2=1%，声速ca=340m/s，空气的密度ρa=1.225kg/m3。

双层微穿孔管消声器传递损失理论计算及有限元Virtual.Lab数值计算结果如图2所示。

图2 双层微穿孔管消声器传递损失计算值与仿真值对比

由图2可知，传递矩阵法计算结果与有限仿真结果在整个频域内吻合良好，故该理论模型的正确性得到验证，进而传递矩阵法被应用于双层微穿孔管消声器声学性能分析。

2.2 声学性能分析

设定双层微穿孔管消声器的内插管长度l1=l2=10mm，穿孔率φ1=φ2=2%，其他参数不变。图3为不同穿孔段长度对消声器声学性能的影响。从图3可以看出：随着穿孔管长度的增加，低频的消声性能下降，而中高频的消声性能得到改善，并且固有频率的峰值前移，频带变窄。

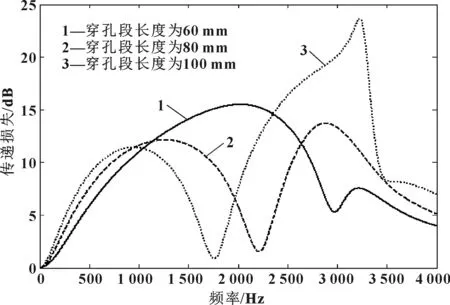
图3 穿孔段长度对消声器声学性能的影响

图4为不同外层膨胀腔厚度对消声器声学性能的影响。由图4可知：随着外层膨胀厚度的增加，低频的消声量得到改善，而高频的消声效果变差。因此增加外层膨胀厚度可改善中低频的消声性能。

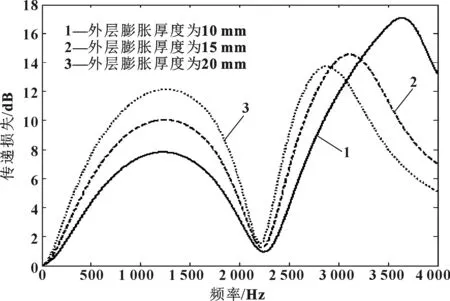
图4 外层膨胀腔厚度对消声器声学性能的影响

图5为不同穿孔直径对消声器声学特性的影响。从图5可以看出：随着孔径的增大，低频消声量变化不明显，但高频消声性能明显变差。因此，微穿孔管消声器的孔径不应太大。

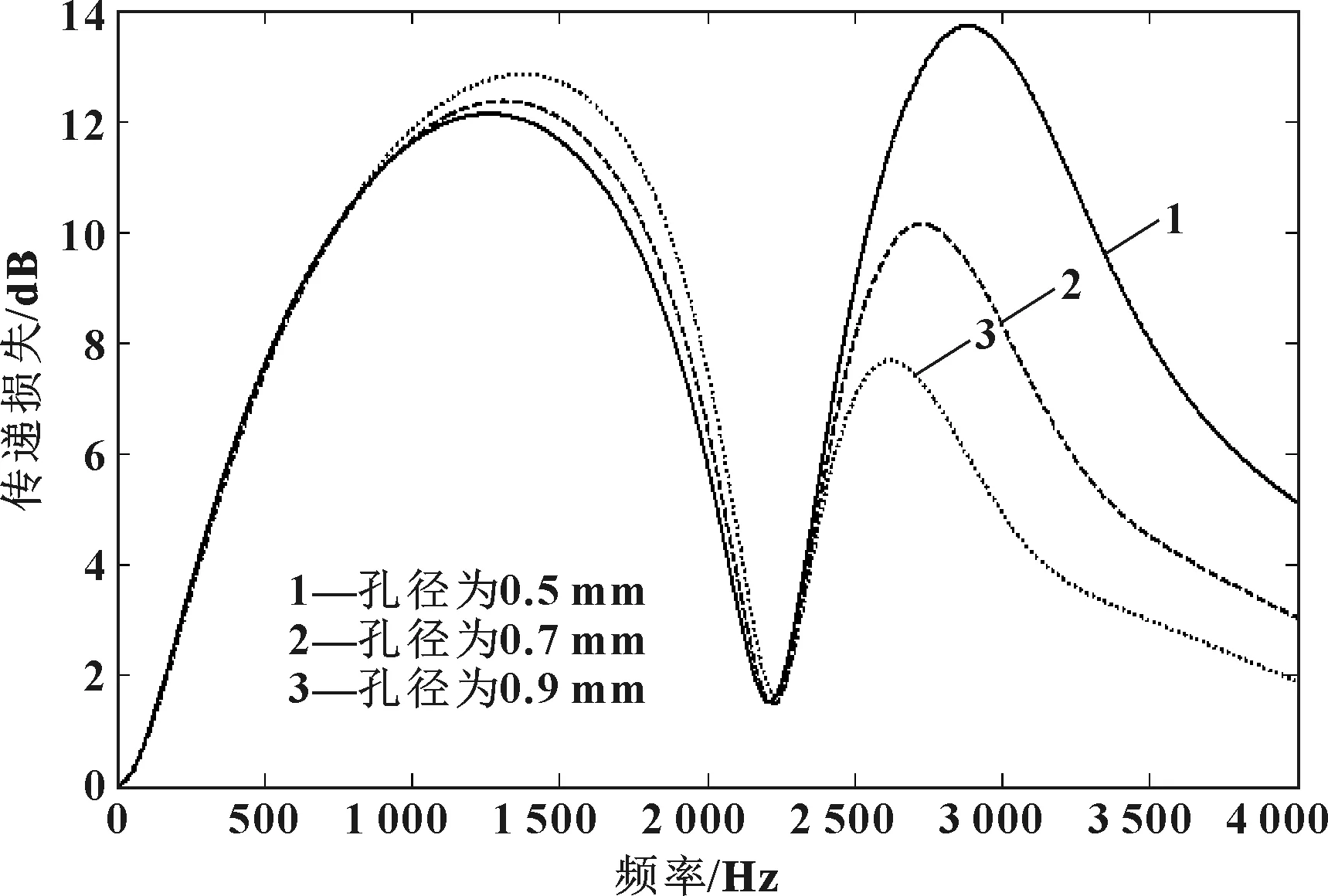
图5 穿孔直径对消声器声学性能的影响

3 结论

基于微穿孔板吸声理论和一维平面波理论，建立了双层微穿孔管消声器声学理论模型，与有限元计算结果进行对比，验证了传递矩阵法的正确性。通过数值分析发现，在不同的频段内，结构参数对消声器的消声效果的影响不同。增加穿孔段长度可以改善双层微穿孔管消声器中高频的消声性能，而低频消声性能变差。增加外层膨胀厚度对双层微穿孔管消声器的低频有效，而对高频无效。穿孔直径对双层微穿孔管消声器低频影响不大，而高频消声效果变差。因此，需要针对不同的频率范围和消声效果，对双层微穿孔管消声器进行结构优化。由于文中方法在结构参数变化时不需要重新编程和划分网格，相对于有限元法具有较高的计算效率，因此，此方法对多层微穿孔管消声器的设计和优化具有一定的指导意义。