涌泉根灌不同浓度肥液入渗特性及土壤湿润体模型研究

何振嘉，傅渝亮，王 博，费良军



涌泉根灌不同浓度肥液入渗特性及土壤湿润体模型研究

何振嘉1,2，傅渝亮3，王 博4，费良军5

（1. 陕西省土地工程建设集团有限责任公司，西安 710075；2. 国土资源部退化及未利用土地整治工程 重点实验室，西安 710075；3. 华北水利水电大学水利学院，郑州 450045；4. 陕西核工业工程勘察院有限公司，西安 710054；5. 西安理工大学水资源研究所，西安 710048）

为了研究涌泉根灌肥液入渗特性及湿润体水氮运移的变化规律，在陕北米脂山地微灌枣树示范基地原状土上进行了涌泉根灌肥液入渗试验。结果表明：累积入渗量与入渗时间之间符合Kostiakov幂函数关系（2>0.9，<0.01）；涌泉根灌入渗能力与增渗效果均随肥液浓度增大而增大；水平湿润锋与竖直湿润锋运移距离均随肥液浓度增大而增大，且均与入渗时间呈显著的幂函数关系，水平方向和竖直方向的湿润锋运移距离的拟合值与实测值的相对误差在–3.84%～5.20%以内。肥液浓度的不同对于湿润体大小略有影响。提出了涌泉根灌肥液入渗湿润体内土壤含水率和NH4+-N浓度分布的数学模型，即在一定浓度范围内，单位含水率的变化可引起的肥液浓度变化，且模型的计算精度较高（模拟值与实测值相对误差在10%以内），并符合湿润体内土壤含水率和NH4+-N分布规律，可对不同位置处土壤含水率及NH4+-N含量进行估算。水分分布情况对肥液浓度条件敏感性较低，NH4+-N分布情况对肥液浓度条件敏感性较高。研究可为涌泉根灌水肥高效利用提供参考。

入渗；氮；土壤；涌泉根灌；肥液入渗；湿润体；数学模型；水氮分布

0 引 言

涌泉根灌是一种可直接将水肥输送到果树根部进行灌溉的地下微灌技术，具有减少水肥蒸发，提高水肥利用效率的优势[1-2]。涌泉根灌器的制作也较为简单，价格较滴灌系统更为低廉，所需材料容易获取。并且涌泉根灌使得相关配套微灌设施的使用寿命较高，而相对微灌系统相关配套设备的投入较低[3]。同时，由于灌水器套管的保护，避免了灌水器滴头堵塞，较其他微灌优势明显[4]。近年来，国内外学者对点源入渗条件下滴头流量和湿润体特性之间的关系以及微灌湿润体水分入渗方面进行了大量研究，取得了众多成果[5-10]。Kohn等[11-12]通过灌水器地埋试验，证明了将灌水器埋于地下，水分利用效率可显著提高；Cote等[13-15]利用Hydrus模型对滴灌条件下水分运移情况进行了模拟，研究表明土壤质地和灌水量对湿润体形状有较大影响；Skaggs等[16]通过数值模拟，模拟了不同初始含水率、不同土壤质地条件对滴灌水分运移的影响，结果表明湿润锋运移和湿润体内部水分分布受土壤质地及土壤初始含水率影响较大。刘显等[17]进行了涌泉根灌不同灌水器埋深条件下土壤水分入渗试验，结果表明，灌水器埋深对湿润锋运移起到显著的影响。费良军等[18]研究了涌泉根灌在不同土壤容重条件下湿润体的特性，结果表明，土壤容重越大，湿润锋运移距离及湿润体内水分含量越小。黎朋红等[19]和费良军等[20]通过大田试验，证明了湿润锋运移距离随灌水器流量的增大而增大。李耀刚等[21-23]利用Hydrus-3D软件模拟了涌泉根灌水分运动，结果表明，流量与水分运移速率、湿润锋运移速率以及土壤含水率呈正相关关系，与湿润体体积呈负相关关系。李卓等[24]研究不同容重条件下的水分入渗，结果表明入渗能力与土壤容重呈负相关关系，入渗速率的参数与土壤容重呈正相关关系。樊晓康等[25]研究了不同土壤初始含水率、土壤干容重和灌水器埋深对湿润体的影响，结果表明初始含水率及土壤容重对湿润体的形状影响不显著。吴恒卿等[26]做了双点源入渗试验，结果表明滴头流量和滴头间距对涌泉根灌湿润体的运移距离、交汇时间、土壤含水率分布均有一定影响。牛文全等[27]做了室内入渗试验，结果表明各方向湿润锋运移距离随土壤初始含水率的增大而增大。费良军等[28]分析了入渗湿润深度范围内肥液浓度对土壤NO3–-N和NH4+-N含量分布特性的影响，结果表明涌泉根灌肥液浓度在50 g/L以内时，入渗量与湿润锋运移距离均与入渗时间呈极显著幂函数关系，且分别分析了入渗阶段和再分布阶段的水分、氨氮及硝氮运移分布影响，但未考虑土壤水分分布和铵态氮分布之间的湿润体函数变化关系。

综上所述，国内外对微灌以及涌泉根灌土壤水分运动规律进行了深入探讨，但其研究重点多从湿润体土壤水分运动特性等方面开展，不同肥液浓度涌泉根灌入渗条件下湿润体特性研究较单一，无法明确湿润体内部土壤含水率与铵态氮浓度之间的函数变化关系。本文通过涌泉根灌条件下不同肥液浓度湿润体入渗试验，分析了肥液入渗对土壤水分入渗、湿润体特征及铵态氮运移的影响，并研究土壤水分分布及铵态氮运移分布影响，以及由含水率分布变化引起的铵态氮浓度变化的函数关系，以期为涌泉根灌水肥高效利用提供参考。

1 材料与方法

1.1 试验地概况

试验在陕西榆林市米脂县远志山西北农林科技大学试验基地进行，本区地形为黄土高原丘陵沟壑，气候为半干旱性，根据米脂气象局提供的1971—2016年逐日气象资料统计，雨季为每年的7—9月，年均降水量451.6 mm。试验区土壤为黄绵土，其<0.002、0.002～<0.02、0.02～<0.20、0.2～2.0 mm粒径占比分别为17.55%、42.59%、38.86%、1.00%。土壤平均干容重为1.31 g/cm3，土壤初始含水率为10.4%，土壤田间持水量为23.4%，土壤饱和含水率39.8%，有效N、P、K质量分数分别为34.7、2.9、101.9 mg/kg，有机质质量分数是0.21%，土壤平均NH4+-N质量分数为0.89 mg/kg。

1.2 试验装置及试验设计

涌泉根灌入渗试验由带有刻度的截面积为70.88 cm2的硬质塑料制作而成的马氏瓶进行自动供水。灌水器模拟滴头流量为5 L/h，灌水量30 L，试验氮肥选用易溶性的尿素（CO(NH2)2）（氮素质量分数≥46.4%）作为试供肥料，设定肥液浓度梯度分别为5、10 和20 g/L，清水为对照（肥液浓度为0）。涌泉根灌灌水器上方有连通大气的气孔，马氏瓶提供恒定水头，通过调节马氏瓶底部旋钮开度控制流量，用秒表和20 mL的量筒来滤定滴头流量，并校验试验过程中部分时刻的灌水器流量，确保供水稳定。

涌泉根灌灌水器高30 cm，灌水器埋深15 cm，外径4 cm，灌水器与配套套筒通过螺口直接安装或拆卸，配套套筒（PVC材料）壁厚2 mm，内径4 cm，外径4.2 cm；在灌水器配套套管自下往上每隔2 cm打一个孔洞，孔径为2 mm，开孔度20%，开孔部分用纱布包裹，防止土壤颗粒进入灌水器产生堵塞。涌泉根灌示意图如图1所示。

1.3 试验方法及观测内容

将试验区原状土剖面作为观测面进行不同肥液浓度试验，试验系统如图2所示。进行不同肥夜浓度试验时，观测或计算湿润锋运移距离、累积入渗量及NH4+-N含量。为降低降雨和蒸发对湿润体的影响，试验结束后用塑料布遮盖湿润体。

图1 涌泉根灌示意图

图2 试验系统示意图

=π12+0.2×2π1() （1）

不同肥液浓度条件下累积入渗量曲线用Kostiakov[28]入渗模型进行描述，形式如下：

入渗率是在单位时段内通过单位面积的水量，由累积入渗量除以入渗时间确定，入渗时间由精度为0.01 s的秒表确定，不同时刻湿润锋运移距离使用钢卷尺直接在试验剖面上量出。土壤含水率采用烘干法获得，在灌水器处、距灌水器12.5 cm以及距灌水器25 cm处取土，在垂直深度0～100 cm范围内每隔10 cm测定不同时间段土壤含水率。在入渗阶段与再分布过程中均做3次重复以避免入渗阶段取土损伤影响再分布过程中相同位置处含水率测量准确度，所有含水率数据均取均值。

土壤NH4+-N含量使用CleverChem200全自动间断化学分析仪（德国DeChem-Tech.GmbH）测定。NH4+-N测定方法：在碱性条件下，铵离子和次氯酸盐，水杨酸钠发生反应生成显色的复合物，整个反应是在硝普钠的催化下进行，在660 nm波长下比色测定。

不同肥液浓度对水分及氮素分布情况的影响程度通过计算肥液浓度的变化程度对分析指标的影响确定，如下式[29]：

1.4 数据分析

采用Microsoft Excel 2007分析软件处理试验数据并进行绘图。

2 结果与分析

2.1 肥液浓度对入渗特性的影响

图3a和图3b分别为肥液浓度分别为0、5、10和20 g/L时累积入渗量及入渗率的变化曲线。由图可以看出，随着入渗时间增长，累积入渗量呈增大趋势，入渗率逐渐降低。从入渗开始，浓度为5和10 g/L累积入渗量差异不大，10和20 g/L累积入渗量差异较明显，随着时间增加，不同梯度间差异逐渐显著，入渗率逐渐减小，最终趋于稳定。这可能主要是因为肥液使土壤结构发生了改变，水分入渗通道不断增加，带有负电荷的土壤胶体被肥液中大量带有相反电荷的NH4+离子中和，使胶体之间排斥作用减弱甚至消失，微小胶体凝聚形成土壤团聚体，增加了土壤颗粒粒径，使得入渗能力增强。

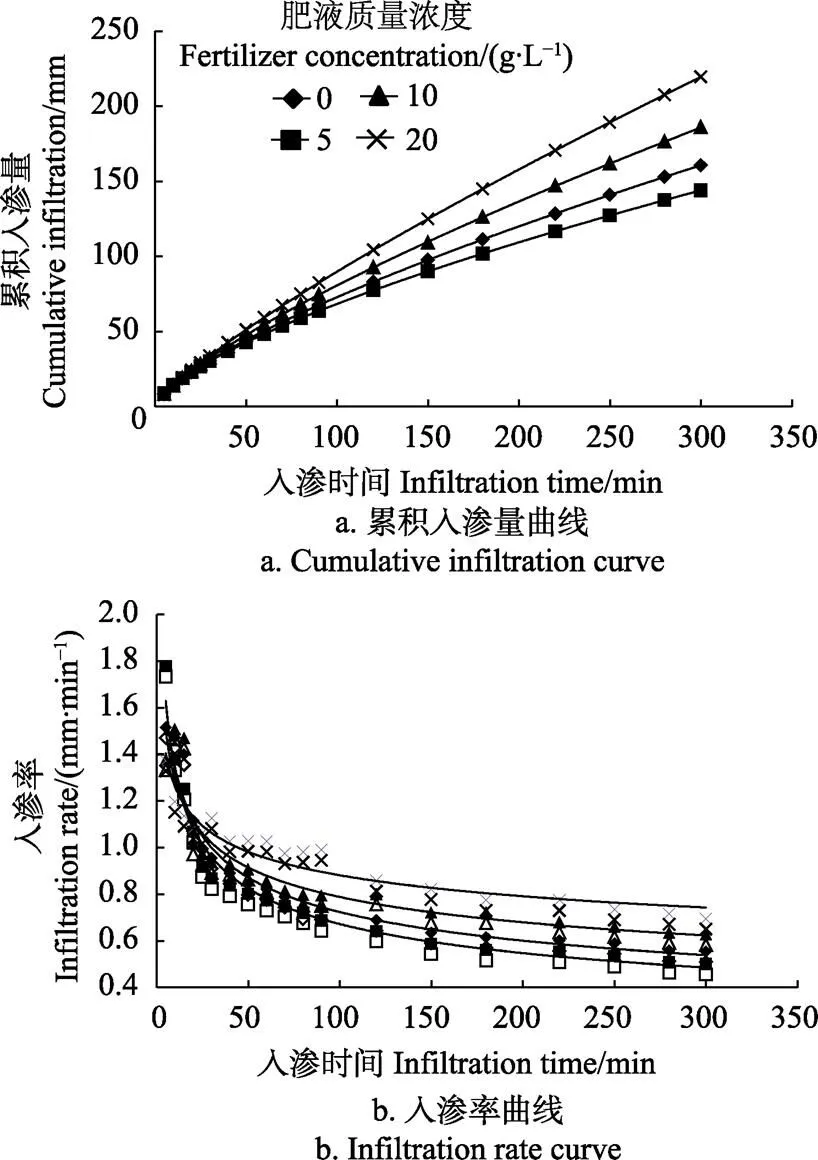
图3 肥液浓度对涌泉根灌累积入渗量及入渗速率的影响

为了量化肥液浓度对于土壤水分入渗的增渗效果，利用增渗率（同一入渗时刻，肥液浓度的累积入渗量较清水的增加量，并与清水累积入渗量的百分比，%）进行具体分析，结果如表1。

表1 累积入渗量与增渗率

表1为不同肥液浓度不同灌水历时累积入渗量与增渗率的比较。由表可以看出，各入渗时间，累积入渗量及增渗率均随肥液浓度增加而增大。采用Kostiakov入渗模型（式（2））对不同肥液浓度条件下累积入渗量曲线进行拟合，结果见表2。不同肥液浓度模拟出来的决定系数2均大于0.9，大于显著性水平0.01时的临界值（0.606），表明Kostiakov模型能够很好地描述涌泉根灌累积入渗量随时间变化关系。

表2 累积入渗量Kostiakov模型拟合参数

2.2 肥液浓度对湿润体特性的影响

2.2.1 肥液浓度对湿润锋特性的影响

图4为肥液浓度分别为0、5、10和20 g/L时湿润锋运移距离的变化曲线。水平、竖直向下、竖直向上湿润锋运移距离均随入渗时间增长而增加，随着肥液浓度越大，水平湿润锋运移距离略有增大，但差异较小；竖直方向湿润锋运移距离逐渐增大。涌泉根灌条件下肥液入渗在水平、竖直向下、竖直向上湿润锋运移距离与时间的关系符合幂函数关系（表3，2>0.9，<0.01），函数形式如式（5）所示，函数拟合参数如表3所示。

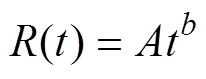
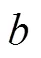
将式（6）～式（11）分别代入式（5）得到涌泉根灌水平方向和竖直向下、以及竖直向上湿润锋运移距离随时间和肥液浓度变化的数学模型：

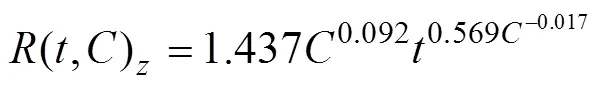
式中(,)为涌泉根灌不同肥液浓度条件下水平湿润峰随时间变化的运移距离，cm；(,)为涌泉根灌不同肥液浓度条件下竖直向下湿润峰随时间变化的运移距离，cm；(,)为涌泉根灌不同肥液浓度条件下竖直向上湿润峰随时间变化的运移距离，cm；为肥液浓度，g/L。

为验证模型的可靠性，以灌水器埋深15 cm，肥液浓度23 g/L为例，使用式（12）～式（14）得到各方向湿润锋运移距离模拟值，见表4。水平方向和竖直方向的湿润锋运移距离的拟合值与实测值的相对误差在–3.84%～5.20%以内，满足精度要求。

注：灌水器出水口位置为坐标原点。

表3 湿润锋运移距离幂函数拟合结果

注：()为湿润锋运移距离，cm。为入渗时间，min。

Note:() is wetting front shift distance, cm.is infiltration time, min.

2.2.2 肥液浓度对湿润体体积的影响

以灌水器埋深面将湿润面分为上、下两部分，下部为半椭球，上部为半椭球的一部分。用椭圆方程表示，令：

分别将不同方向湿润锋运移模型（式（12）～式（14））代入椭圆方程，得上半椭圆方程为：

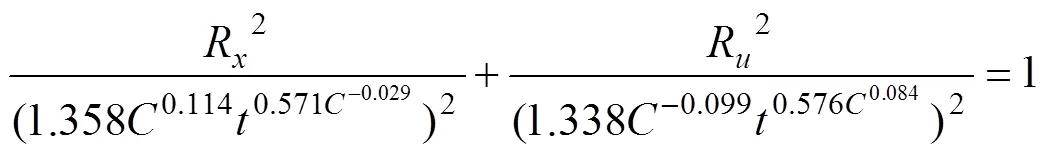
下半椭圆方程为：

根据灌水结束时不同方向湿润锋运移距离，按照式（16）及式（17）计算灌水器不同肥液浓度条件下湿润体体积，结果如表5。可以看出，随着肥液浓度越大，湿润体体积逐渐增大，增幅（施加肥液与清水灌溉湿润体体积的差值除以清水灌溉湿润体体积，%）分别达11.77%、15.01%、15.72%。肥液浓度的不同对于湿润体大小略有影响，但不能采用增大或减小肥液浓度的方式来调控湿润区域。

2.2.3 肥液浓度对湿润体土壤含水率分布的影响

图5a为灌水结束时相同肥液浓度条件下距离灌水器位置不同处土壤含水率曲线。图5b为灌水结束时不同肥液浓度条件下灌水器出水口处土壤含水率曲线。图5c为灌水结束、再分布1d以及3d时在距灌水器出水口25 cm 处不同土壤深度含水率数据，并对不同时间不同空间土壤含水率进行分析。

表4 水平方向和竖直方向湿润锋运移距离实测值和模拟值

表5 不同肥液浓度条件下湿润体体积

由图5a、图5b可以看出，在同一肥液浓度条件下，土壤含水率随距灌水器出水口距离的增大而减小；肥液浓度不同，土壤含水率分布有明显差异，土壤含水率随肥液浓度的增大而增大。由图5c可以看出，同一肥液浓度，随着时间的推移，土壤含水率总体降低。灌水结束到再分布1 d后这一阶段，土壤深度0～60 cm含水率减小幅度较大，60～100 cm深度含水率略有增大，说明在灌水结束到再分布1 d后时段内，土壤水分继续下渗，但下渗程度较小，说明田间条件下，这一深度水分入渗已较为缓慢。再分布1 ～3 d这一阶段，含水率变化显著，呈现出0～60 cm深度减小，60～100 cm增大的规律，在深度80 cm以下区域，含水率波动较小，说明在此区域以下，水分入渗能力更小。

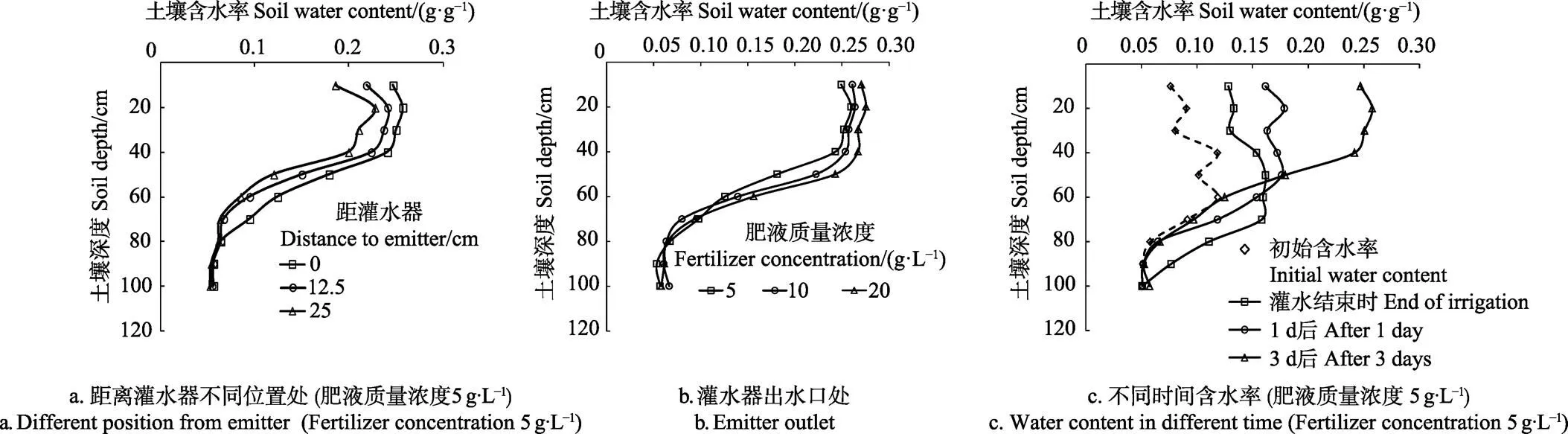
图5 肥液浓度对土壤含水率影响

涌泉根灌肥液自由入渗湿润体内土壤含水率分布模型为[30]

以肥液浓度为5 g/L为例，根据试验资料，有：

为验证模型精度，以灌水器埋深15 cm，土壤初始含水率为4.13%为例，使用式（21）得到含水率模拟值，见表6。可以看出，使用该模型对湿润体内部部分点位含水率进行计算，所得模拟值与实测值相对误差在–5.20%～4.19%以内，具有较高精度，可对不同位置处土壤含水率进行估算。

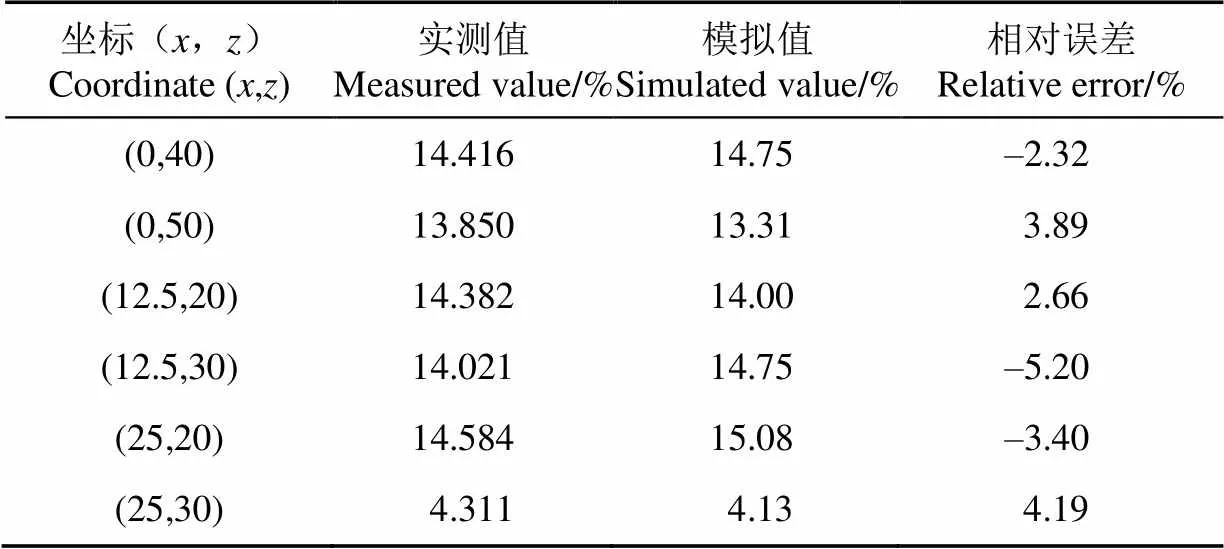
表6 土壤含水率实测值和模拟值

2.2.4 肥液浓度对涌泉根灌NH4+-N含量的影响

分别测得灌水结束、再分布1 d以及3 d不同土壤深度NH4+-N数据，并对不同时间不同空间NH4+-N含量进行分析。图6a为灌水结束时相同肥液浓度条件下距离灌水器位置不同处NH4+-N含量。图6b为灌水结束时不同肥液浓度条件下距离灌水器位置相同处NH4+-N含量。图6c为灌水结束、再分布1 d及3 d时NH4+-N含量。图6d为不同土壤深度NH4+-N含量随时间变化情况。

图6 不同肥液浓度对NH4+-N含量的影响

由图6a可以看出，灌水结束时，同一灌水器埋深条件下，距离灌水器越远，NH4+-N含量越低，这是因为NH4+-N带正电荷，易被带负电荷土壤胶体所吸附，因此入渗溶液中NH4+-N含量减少，使得主要通过扩散机理运移的NH4+-N继续扩散受到阻碍，但随着土壤吸附NH4+-N含量增加到一定程度，在水流的作用下部分NH4+-N继续 向远处运移，其运移受到土壤对NH4+-N吸附能力的影响。由图6b可看出，NH4+-N含量总体上随着肥液浓度增大而增大，由于肥液浓度越大，湿润锋竖向运移距离越大，在土壤深度60～90 cm，NH4+-N也表现为在竖直向下方向迁移也越远。由图6c，同一肥液浓度，随着时间的推移，3 d以内NH4+-N含量逐渐增加，这主要是由于肥液入渗之后，尿素水解逐渐产生NH4+-N。由图6d可以看出，从入渗开始直到入渗结束的3 h，土壤NH4+-N含量增加幅度最大，灌水结束后直到再分布3 d后NH4+-N含量增加幅度逐渐降低。这主要是由于入渗试验过程中，肥液中尿素水解产生大量NH4+-N，导致入渗过程结束后NH4+-N含量突然增大，灌水3 h结束后，没有肥液的进一步补给，水解的NH4+-N逐渐减少，且随着溶液中游离NH4+-N的存在，又对尿素的进一步水解产生抑制作用，水解率有所降低。同时，可以看出，在土壤深度0～30 cm，NH4+-N含量增加较为明显，是初始值的16.4倍（<0.01）、12.7倍（<0.01）、16倍（<0.01）；在深度50 cm及以下，NH4+-N含量增加幅度较小，是初始值的3.5倍（<0.01）。这是因为试验进行时间为中午，地表温度较高，有利于尿素的水解，且地表通气条件较好，有利于NH4+-N的挥发，使得入渗的溶液中游离NH4+-N含量降低，减小了其对尿素进一步水解的抑制作用。

涌泉根灌肥液自由入渗湿润体内土壤NH4+-N分布模型为[30]：

肥液浓度为5 g/L时，根据试验资料，有：

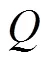
故湿润体内土壤NH4+-N分布模型为：

为验证模型精度，以灌水器埋深15 cm，肥液浓度为3 g/L为例，使用式（25）计算土壤NH4+-N含量，并与实测值进行比较如表7。可以看出，使用该模型对湿润体内部部分点位NH4+-N进行计算，所得计算值与实测值相对误差在10%以内，具有较高精度，可对不同位置处土壤NH4+-N含量进行估算。

表7 土壤NH4+-N质量浓度实测值和模拟值

根据式（20）与式（25），得到5 g/L条件下含水率与铵态氮浓度的关系：

2.3 肥液浓度对涌泉根灌湿润体土壤水、氮分布影响

选取计划湿润深度0～70 cm含水比率（计划湿润层占100 cm土层深度范围含水率的比例）及水分分布均匀程度为分析指标，对于一次灌水，水分分布应以便于作物吸收为主，以试验区枣树为例，根据枣树根区主要分布在水平180 cm，垂直70 cm范围的特点，此处选取计划湿润深度0～70 cm含水比率及水分分布均匀程度为分析指标。利用式（3）和式（4）计算得到水分分布情况对不同肥液浓度下土壤水分的敏感系数。（为减轻计算偏差，计划湿润深度0～70 cm含水比率及水分分布均匀程度权重均取0.5），判断不同肥液浓度对水分及氨氮分布情况的影响程度。同理，选取计划湿润层0～70 cm含氮比率及氮素分布均匀程度为分析指标，计算方法同式（3）和式（4）。通过计算肥液浓度的变化程度对分析指标的影响，得到氮素分布情况对不同肥液浓度的敏感系数（为减轻计算偏差，以计划湿润层0～70 cm含氮比率及氮素分布均匀程度权重均取0.5），判断不同肥液浓度对氮素分布情况的影响程度。计算结果见表8。

表8 肥液浓度变化对土壤水及氮分布敏感系数的影响

可以看出，水分分布情况对肥液浓度条件敏感性均较低，即变化肥液浓度对0～70 cm水分比率和水分分布均匀程度2个分析指标影响不大。相对而言，以肥液浓度10 g/L为基准，降低肥液浓度比增大肥液浓度影响更大。降低肥液浓度，0～70 cm水分比率略有升高，幅度极小，这是因为，肥液浓度的变化幅度未能使得水分入渗深度显著超出0～70 cm范围；水分分布均匀程度则明显降低，幅度较大。增大肥液浓度，0～70 cm水分比率几乎无影响，而水分分布均匀程度略有降低。

而NH4+-N分布情况对肥液浓度条件敏感性均较高，变化肥液浓度对0～70 cm NH4+-N比率和NH4+-N分布均匀程度2个分析指标影响较大。降低肥液浓度，0～70 cm NH4+-N比率略有降低，幅度极小，这是因为，肥液浓度的变化幅度未能使得NH4+-N变化深度显著超出0～70 cm范围；降低肥液浓度，NH4+-N分布均匀程度则大幅降低。增大肥液浓度，0～70 cm NH4+-N比率几乎无影响，而NH4+-N分布均匀程度明显降低。

3 结 论

本文通过涌泉根灌肥液入渗试验，对涌泉根灌肥液入渗特性及湿润体水氮运移的变化规律进行了研究，得到主要结果如下：

1）涌泉根灌入渗能力与增渗效果均与肥液浓度呈显著正相关关系；累积入渗量与入渗时间之间符合Kostiakov幂函数模型关系；水平湿润锋与竖直湿润锋运移距离均随肥液浓度的增大而增大，且均与入渗时间呈显著的幂函数关系。灌水结束时，相同肥液浓度在同一灌水器埋深条件下，距离灌水器越远，NH4+-N含量越低，在灌水器出水口位置附近NH4+-N含量达到峰值。同一土层深度处，土壤NH4+-N随着肥液浓度增大而增大。由于试验设置滴头流量为5 L/h，在入渗过程中，套管内已经为满蓄状态，灌水器内水头已高于出流孔，产生了一部分多余水分无法入渗到土壤中，由试验结果来看，建议设置滴头流量为小于5 L/h时，水量可能完全渗入，灌水器与套管的契合度会更好，不会产生过量的水分从气孔流出，能更好地发挥涌泉根灌高效灌水的优势。

2）分析了涌泉根灌不同肥液浓度条件下土壤水分分布及土壤NH4+-N分布及其随时间变化规律，提出了涌泉根灌肥液入渗湿润体内土壤含水率和NH4+-N浓度分布的数学模型，即在一定浓度范围内，单位含水率的变化可引起的肥液浓度变化，当（自由入渗土体中任一点至灌水器中心的距离）≤（自由入渗湿润锋至灌水器中心的距离）时，即在湿润体湿润范围内任意点处，湿润体内土壤含水率与铵态氮浓度的相关关系可由幂函数进行表征，当＞时，即在湿润体范围外任意点处，初始肥液浓度与初始含水率的比值为一常数，且模型的计算精度较高，并符合湿润体内土壤含水量和NH4+-N分布规律，可对不同位置处土壤含水率及NH4+-N含量进行估算。

3）水分分布情况对肥液浓度条件敏感性均较低，即变化肥液浓度对计划湿润层0～70 cm含水比率和水分分布均匀程度2个分析指标影响不大。NH4+-N分布情况对肥液浓度条件敏感性均较高，变化肥液浓度对计划湿润层0～70 cm含氮比率和NH4+-N分布均匀程度2个分析指标影响较大。

[1] 刘显，费良军. 灌水器流量对涌泉根灌土壤水氮运移的影响[J]. 排灌机械工程学报，2017，35(10)：903－911. Liu Xian, Fei Liangjun. Transport characteristics of water and nitrogen under bubbled root irrigation with emitter discharge[J]. Journal of Drainage and Irrigation Machinery Engin, 2017, 35(10): 903－911.(in Chinese with English abstract)

[2] 吴普特，朱德兰，汪有科. 涌泉根灌技术研究与应用[J].排灌机械工程学报，2010，28(4)：354－357，368. Wu Pute, Zhu Delan, Wang Youke. Research and application of bubbled-root irrigation[J]. Journal of Irrigation and Drainage, 2010, 28(4): 354－357, 368.(in Chinese with English abstract)

[3] 张志韬，吴普特，张俊英，等. 涌泉根灌土壤湿润体运移模型[J]. 排灌机械工程学报，2013，31(2)：173－179. Zhang Zhitao,Wu Pute,Chen Junying,et al.Prediction model of wetted front migration distance under bubbled-root irrigation[J]. Journal of Drainage and Irrigation Machinery Engin, 2013, 31(2): 173－179.(in Chinese with English abstract)

[4] 张志华，朱德兰，李向明，等. 涌泉根灌灌水器外套材料配方试验研究[J]. 节水灌溉，2013(11)：1－3. Zhang Zhihua, Zhu Delan, Li Xiangming, et al. Experimental study on material formula of bubbled-root irrigation device outer casing[J]. Water Saving Irrigation, 2013(11): 1－3.(in Chinese with English abstract)

[5] 张志刚，李宏，李疆，等. 地表滴灌条件下滴头流量对土壤水分入渗过程的影响[J]. 干旱地区农业研究，2014，32(4)：53－58. Zhang Zhigang, Li Hong, Li Jiang, et al. Effects of different dripper discharge on soil water infiltration under drip irrigation[J]. Agricultural Research in the Arid Areas, 2014, 32(4): 53－58.(in Chinese with English abstract)

[6] 刘晓英，杨振刚，王天俊. 滴灌条件下土壤水分运动规律的研究[J]. 水利学报，1990，21(1)：11－22. Liu Xiaoying, Yang Zhengang, Wang Tianjun. Study on water movement under trickle Irrigation[J]. Journal of Hydraulic Engineering, 1990, 21(1): 11－22.(in Chinese with English abstract)

[7] 孙海燕，李明思，张杰，等. 点源滴灌滴头流量设计模式的试验研究[J]. 石河子大学学报：自然科学版，2005，23(1)：81－84. Sun Haiyan, Li Mingsai, Zhang Jie, et al. Experimental research about dripper discharge design mode for point source drip irrigation[J]. Journal of Shihezi University: Natural Science, 2005, 23(1): 81－84. (in Chinese with English abstract)

[8] Patel N, Rajput T S. Dynamics and modeling of soil water under subsurface drip irrigated onion[J]. Agricultural Water Management, 2008, 95(12): 1335－1349.

[9] Ben-Asher J, Charach G, Zemel A. Infiltration and water extraction from trickle iggigation source:The effective hemisphere model[J]. Soil Scince Society of America Journal, 1986, 50(4): 882－887.

[10] Beggs, R A, Tchobanoglous G, Hills D, et al. Modeling subsurface drip application of onsite wastewater treatment system effluent[EB/OL]. St. Joseph: American Society of Agricultural and Biological Engineers, 2013: 701P0104. doi: 10.13031/2013.15765

[11] Kohn P,Roth A.Plant root watering device: USD456225[P]. 2002-04-30.

[12] Skier M.Bio-degradable plant root watering system: USD5842309[P]. 1998-12-01.

[13] Cote C M, Bristow K L, Charlesworth P B, et al. Analysis of soil wetting and solute transport in subsurface trickle irrigation[J]. Irrigation Science, 2003, 22(34): 143－156.

[14] Bristow K L, Cote C M, Thorbum P J, et al. Wetting and solute transport in trickle irrigation systems[C]//6th Intermational Micro-Conference, 2000: 1－9.

[15] Al-ogaidi A M, Wayayok A, Kamal M R, et al. Modelling soil wetting patterns under drip irrigation using hydrus-3D and comparison with empirical models[C]//Global Conference on Engineering and Technology, 2016.

[16] Skaggs T H, T J Trout, Y Rothfuss. Drip irrigation water distribution pattern: Effects of emitter rate, pulsing and antecedent water[J]. Soil Science Society of America Journal,2012,74(6):1886, doi:10.2136/2009.0341, 2010.

[17] 刘显，费良军，王佳，等. 灌水器埋深对涌泉根灌土壤水氮运移特性的影响[J]. 灌溉排水学报，2016，35(9)：20－25. Liu Xian, Fei Liangjun, Wang Jia, et al. Transport characteristics of water-and nitrogen under bubbled-root irrigation with burled depth of emitter[J]. Journal of Irrigation and Drainage, 2016, 35(9): 20－25.(in Chinese with English abstract)

[18] 费良军，刘显，王佳，等. 土壤容重对涌泉根灌土壤水氮运移特性的影响[J]. 农业机械学报，2017，48(8)：219－228. Fei Liangjun, Liu Xian, Wang Jia, et al. Effects of soil bulk density on transport characteristics of water and nitrogen under bubbled-root irrigation[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(8): 219－228.(in Chinese with English abstract)

[19] 黎朋红，汪有科，马理辉，等. 涌泉根灌湿润体特征值变化规律研究[J]. 水土保持学报，2009，23(6)：190－194. Li Penghong,Wang Youke, Ma Lihui, et al. Study on eigenvalues of wetted soil under bubbled root irrigation[J]. Journal of Soil and Water Conservation, 2009, 23(6): 190－194.(in Chinese with English abstract)

[20] 费良军，曹俊，聂卫波. 涌泉根灌土壤湿润体特性试验[J].排灌机械，2011，29(3)：260－265. Fei Liangjun, Cao Jun, Nie Weibo.Characteristics test of wetting body of surge and spring root irrigation[J]. Journal of Drainage and Irrigation Machinery Engineering, 2011, 29(3): 260－265. (in Chinese with English abstract)

[21] 李耀刚，王文娥，胡笑涛，等. 涌泉根灌条件下土壤水分运动数值模拟研究[J]. 灌溉排水学报，2012，31(3)：42－47. Li Yaogang, Wang Wene, Hu Xiaotao, et al. Numerical simulation of soil water movement under bubbled root irrigation[J]. Journal of Irrigation and Drainage, 2012, 31(3): 42－47.(in Chinese with English abstract)

[22] 李耀刚，王文娥，胡笑涛，等. 基于HYDRUS-3D的涌泉根灌土壤入渗数值模拟[J]. 排灌机械工程学报，2013，31(6)：536－552. Li Yaogang, Wang Wene, Hu Xiaotao, et al. Numerical simulation of soil water infiltration under bubbled root irrigation based on hydrus-3D[J]. Journal of Drainage and Irrigation Machinery Engineering, 2013, 31(6): 536－552.(in Chinese with English abstract)

[23] 李耀刚，王文娥，胡笑涛，等. 涌泉根灌入渗特性影响因素[J]. 水土保持学报，2013，27(4)：114－119. Li Yaogang, Wang Wene, Hu Xiaotao, et al. Influencing factors of infiltration characteristics under bubbled root irrigation [J]. Journal of Soil and Water Conservation, 2013, 27(4): 114－119.(in Chinese with English abstract)

[24] 李卓，吴普特，冯浩，等. 容重对土壤水分入渗能力影响模拟实验[J]. 农业工程学报，2009，25(6)：40－45. Li Zhuo, Wu Pute, Feng Hao, et al. Simulation experiment on effect of soil bulk density on soil infiltration capacity [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(6):40－45.(in Chinese with English abstract)

[25] 樊晓康，陈俊英，牛文全，等. 涌泉根灌土壤湿润体影响因素的试验研究[J]. 节水灌溉，2011(10)：1－4. Fan Xiaokang, Chen Junying, Niu Wenquan, et al. Experimental study on influencing factors of soil wetted body of clay loam under bubbled root irrigation[J]. Water Saving Irrigation, 2011(10): 1－4.(in Chinese with English abstract)

[26] 吴恒卿，黄强，魏群. 涌泉根灌双点源交汇入渗湿润体试验研究[J]. 西北农林科技大学学报：自然科学版，2015，43(5)：201－207. Wu Hengqing, Huang Qiang, Wei Qun. Moist body of two-point source interference infiltration of surge root irrigation[J]. Journal of Northwest A&F University: Natural Science Edition, 2015, 43(5): 201－207.(in Chinese with English abstract)

[27] 牛文全，樊晓康，赵晓波，等. 初始含水率对涌泉根灌土壤渗透特征的影响[J]. 排灌机械工程学报，2012，30(4)：491－496. Niu Wenquan, Fan Xiaokang, Zhao Xiaobo, et al. Effect of initial water content on soil infiltration characteristics during bubble irrigation[J]. Journal of Drainage and Irrigation Machinery Engineering, 2012, 30(4): 491－496.(in Chinese with English abstract)

[28] 费良军，傅渝亮，何振嘉，等. 涌泉根灌肥液入渗水氮运移特性研究[J]. 农业机械学报，2015，46(6)：121－129. Fei Liangjun, Fu Yuliang, He Zhenjia, et al. Transport characteristics of water and nitrogen under bubbled-root irrigation with fertilizer solution[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(6): 121－129. (in Chinese with English abstract)

[29] 王博. 涌泉根灌入滲土壤水氮运移特性试验与数值模拟[D]. 西安：西安理工大学，2015. Wang Bo. Experimental and Numerical Simulation of Water and Nitrogen Transport Characteristics in Soils under the Bubbled-root Irrigation[D]. Xi’an: Xi’an University of Technology, 2015.(in Chinese with English abstract)

[30] 费良军，程东娟，朱兴华. 单膜孔点源肥液入渗水氮分布特性试验研究[J]. 农业工程学报，2006，22(10)：12－15. Fei Liangjun, Cheng Dongjuan, Zhu Xinghua. Water and NO3--N distribution characteristics in single film hole point source fertile solution infiltration[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2006, 22(10): 12－15.(in Chinese with English abstract)

Infiltration characteristics and wetting body model of bubbled-root irrigation under different fertilizer concentration

He Zhenjia1,2, Fu Yuliang3, Wang Bo4, Fei Liangjun5

(1.710075,; 2.710075,; 3.450045,; 4.710054,; 5.710048,)

Bubbled-root irrigation is an effective method of irrigation that transports water and fertilizer to roots of fruit trees. This study investigated the infiltration characteristics of the bubbled-root irrigation and the changes of water and nitrogen transport in the wetting body. A field experiment was carried out in Yulin city, Shanxi. During the experiment, water was supplied by a Markov bottle. The emitter flow rate was 5 L/h. The irrigation amount was 30 L. The nitrogen-fertilizer was urea with nitrogen not less than 46.4%. The fertilizer concentration was 5, 10 and 20 g/L. The irrigation without fertilizer was as control. The cumulative infiltration was determined and it dynamic change was fitted by a Kostiakov model. The infiltration-increasing rate was calculated by difference between cumulative infiltration of fertilizer treatments and that of control dividing by the cumulative infiltration of control. In addition, the water content and ammonium N content were measured. Soil samples along the profile 0-100 cm (in an interval of 10 cm) were collected from the position where the emitter was, at the distance of 12.5 and 25 cm away from the emitter, respectively. The sensitivity of water distribution and nitrogen distribution in soils was assessed by comprehensive sensitivity coefficient when the fertilizer concentration increased by 100 g/L or decreased by 50 g/L. The results showed that the cumulative infiltration increased with infiltration time following a Kostiakov power function model (2>0.9). The infiltration rate decreased with time. The cumulative infiltration and infiltration-increasing rate both increased with increasing fertilizer concentration. The wetting front shift distance increased with infiltration time. When the fertilizer concentration increased, the horizontal wetting front shift distance increased slightly but the vertically upward and downward wetting front shift distance increased greatly. Models of wetting front shift distance based on fertilizer concentration and infiltration time were established. It had a high accuracy and the relative error between measured and simulated value was -3.84%-5.20%. The fertilizer concentration could slightly affect the volume of wetted body. Models were established to estimate soil water content and NH4+-N concentration of bubbled-root irrigation under different fertilizer concentrations. Both of the models had the high accuracy with the relative error between measured and estimated values less than 10%. The models could estimate the soil water content and NH4+-N content at different locations. Within the wetted body, the relationship between soil water content and NH4+-N content could be described by power functions, while in the outside of the wetted body, the ratio of initial fertilizer concentration to initial soil water content was a constant. The change of fertilizer concentration could be caused by the change of unit water content within a certain concentration range. At the end of irrigation, NH4+-N content decreased with increasing the distance away from the emitter at the same buried depth of emitter. It increased with the increase in the fertilizer concentration. The NH4+-N content increased greatly before 3 h and the increase amplitude gradually decreased after 3 days. The comprehensive sensitivity coefficient of water distribution to fertilizer concentration change was 0.029-0.076 while that of NH4+-N distribution was 0.148-0.662. It indicated that the water distribution was less sensitive to fertilizer concentration, and the distribution of NH4+-N was more sensitive to fertilizer concentration.

infiltration; nitrogen; soils; bubbled-root irrigation; fertilizer solution infiltration; wetted body; mathematical model; water and nitrogen distribution

何振嘉，傅渝亮，王 博，费良军.涌泉根灌不同浓度肥液入渗特性及土壤湿润体模型研究[J]. 农业工程学报，2018，34(24)：90－99. doi：10.11975/j.issn.1002-6819.2018.24.011 http://www.tcsae.org

He Zhenjia, Fu Yuliang, Wang Bo, Fei Liangjun. Infiltration characteristics and wetting body model of bubbled-root irrigation under different fertilizer concentration[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(24): 90－99. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.24.011 http://www.tcsae.org

2018-03-31

2018-11-10

国家自然科学基金资助项目（51279157）；“十二五”国家科技支撑计划（2011BAD29B04）

何振嘉，工程师，主要从事节水灌溉与土地工程方面研究。Email：471128226@qq.com

10.11975/j.issn.1002-6819.2018.24.011

S275.4

A

1002-6819(2018)-24-0090-10