蓖麻茎秆弯曲力学特性试验及仿真分析

侯俊铭，白晶波，杨 勇，姚恩超

（沈阳农业大学工程学院，沈阳 110866）

蓖麻为油料作物，含油量为35%～57%，经济价值很高[1-2]。蓖麻籽油及其衍生物广泛应用于化工、医药、国防等领域[3-4]。收获是蓖麻生产加工过程重要环节。我国大部分地区依靠人工收获，劳动强度高、损失率大，严重影响蓖麻收获产量。实现蓖麻机械化收获将有助于提高蓖麻产量。蓖麻茎秆切割装置是蓖麻收获机械关键部件，在切割过程中，茎秆与割刀接触区域可产生复杂应力和变形，影响切割效果。

沈成等通过拉伸、压缩、弯曲等力学试验，获得苎麻茎秆力学模型全部参数[5]。Tavakoli等探讨不同试验条件对玉米秸秆剪切强度和剪切能影响[6]。李小城等测定小麦茎秆弹性模量和抗弯刚度，分析剪切特性[7-8]，Chandio等对比分析不同加载速率对小麦和水稻秸秆剪切特性影响[9]。Ince等探讨不同条件下向日葵秸秆弯曲和剪切特性[10]。Džugan等在甘蔗粉碎机上模拟工作加载条件，探究甘蔗动态力学特性[11]。王伟等对木薯茎秆上、中、下三部分作压缩、弯曲试验，获得收获期木薯茎秆抗弯强度和压缩强度[12]。黄汉东等和施印炎等利用有限元计算方法分别研究甘蔗和芦蒿在破坏载荷下破损形态及应力应变分布[13-14]。有限元法可分析作物茎秆内部复杂应力应变规律，广泛应用于农业科学领域[15]。蓖麻茎秆结构复杂，利用有限元法从微观角度研究其弯曲力学特性鲜有报道。

蓖麻茎秆在不同含水率、载荷加载部位、加载速率等条件下弯曲力学特性差异较大。为揭示各因素对茎秆抗弯强度影响，本文以通辽地区广泛种植通蓖7号和通蓖17号蓖麻茎秆为研究对象，在不同试验组合下开展蓖麻茎秆弯曲试验，获得各因素对茎秆抗弯强度影响规律；从茎秆微观角度，结合有限元法分析蓖麻茎秆纤维导管含量（导管-茎秆体积比）对抗弯强度影响，验证加载部位对抗弯强度影响取决于该部位纤维导管含量。蓖麻茎秆弯曲力学特性研究，可为开发蓖麻收获机构提供理论依据。

1 材料与方法

1.1 材料

试验采用通辽地区广泛种植通蓖7号（蒴果无刺）和通蓖17号（蒴果有刺）蓖麻茎秆，取样方法为随机取样，蓖麻茎秆取地表至一级蓖麻蒴果结果位置一段主茎。试验材料通直，无病虫害，少分支。

1.2 试验装置

试验设备主要有VHX-5000超景深显微镜[基恩士（中国）有限公司]、WDW-2型微机电子万能试验机（美特斯工业系统有限公司，2000N）、101-OA型数显示电热恒温干燥箱、CP423S电子天平（精度1 mg）、游标卡尺（精度0.02 mm）、密封袋等。试验于2017年11月在沈阳农业大学工程学院实施。

1.3 试验方法

在已获得蓖麻茎秆含水率及主茎高度基础上，选取蓖麻茎秆含水率（%）X1、施加载荷部位（mm）X2、施加载荷速率（mm·min-1）X3为变量，以茎秆最大抗弯强度为试验指标，采用三元二次回归通用旋转组合设计，将各因素按其水平及取值范围作因素编码，加载部位定义为以蓖麻茎秆根部为坐标轴原点，沿茎秆生长方向建立坐标轴，加载点距根部坐标原点距离即为加载部位。试验方案如表1所示。弯曲试验方法参照GB/T14452-1993金属弯曲力学性能试验方法。

选用WDW-2型微机电子万能试验机（最大负载2000 N）作弯曲试验。试验时，将茎秆试样放入工作平台，压头对茎秆施加弯曲载荷。每组试验取3个试样作测试，将图1中最大值作为抗弯强度表征量。

1.4 弯曲破坏过程

茎秆抗弯强度与茎秆含水率相关，两种蓖麻茎秆在含水率10%、15%、20%条件下作弯曲破坏测试。得出蓖麻茎秆出现裂纹位置主要集中在压头附近，且与茎秆含水率相关。当含水率较低（10%）时，茎秆呈脆性，压头附近产生裂纹，向茎秆两端扩展，形成贯穿裂纹。当含水率增加时，茎秆韧性增强，裂纹主要在压头正下方，无明显贯穿裂纹出现。相同条件下弯曲试验，通蓖17号蓖麻茎秆抗弯强度小于通蓖7号，茎秆更易变形。

通蓖7号和通蓖17号蓖麻茎秆在10%、15%、20%含水率条件下得到应力-应变曲线见图1。

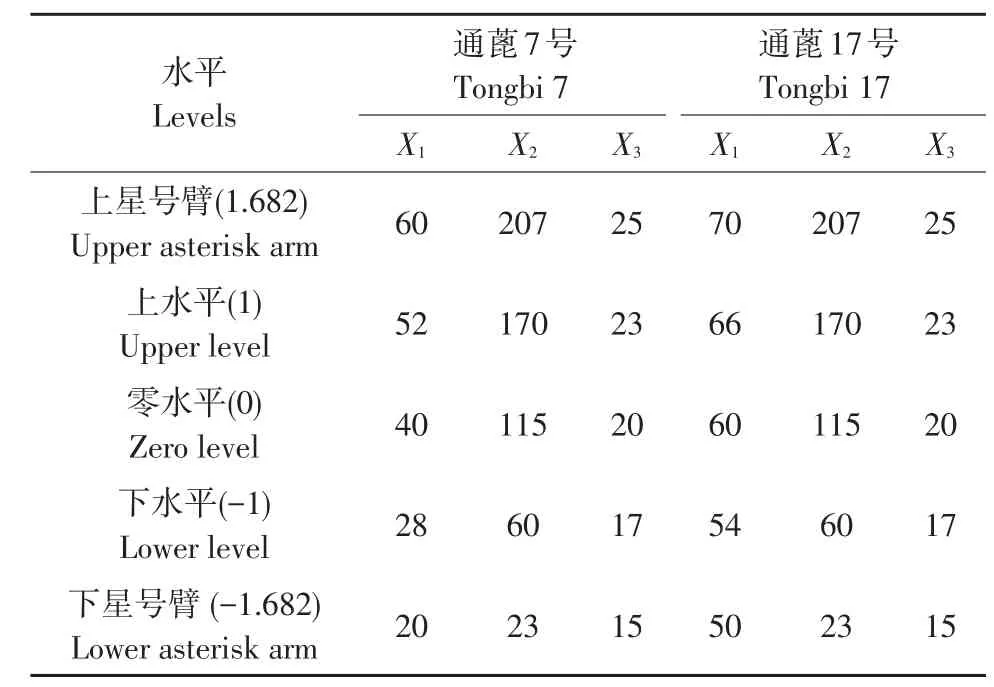
表1 通蓖7号和通蓖17号试验因素编码Table1 Coding of factorsand levelsof Tongbi7 and Tongbi17

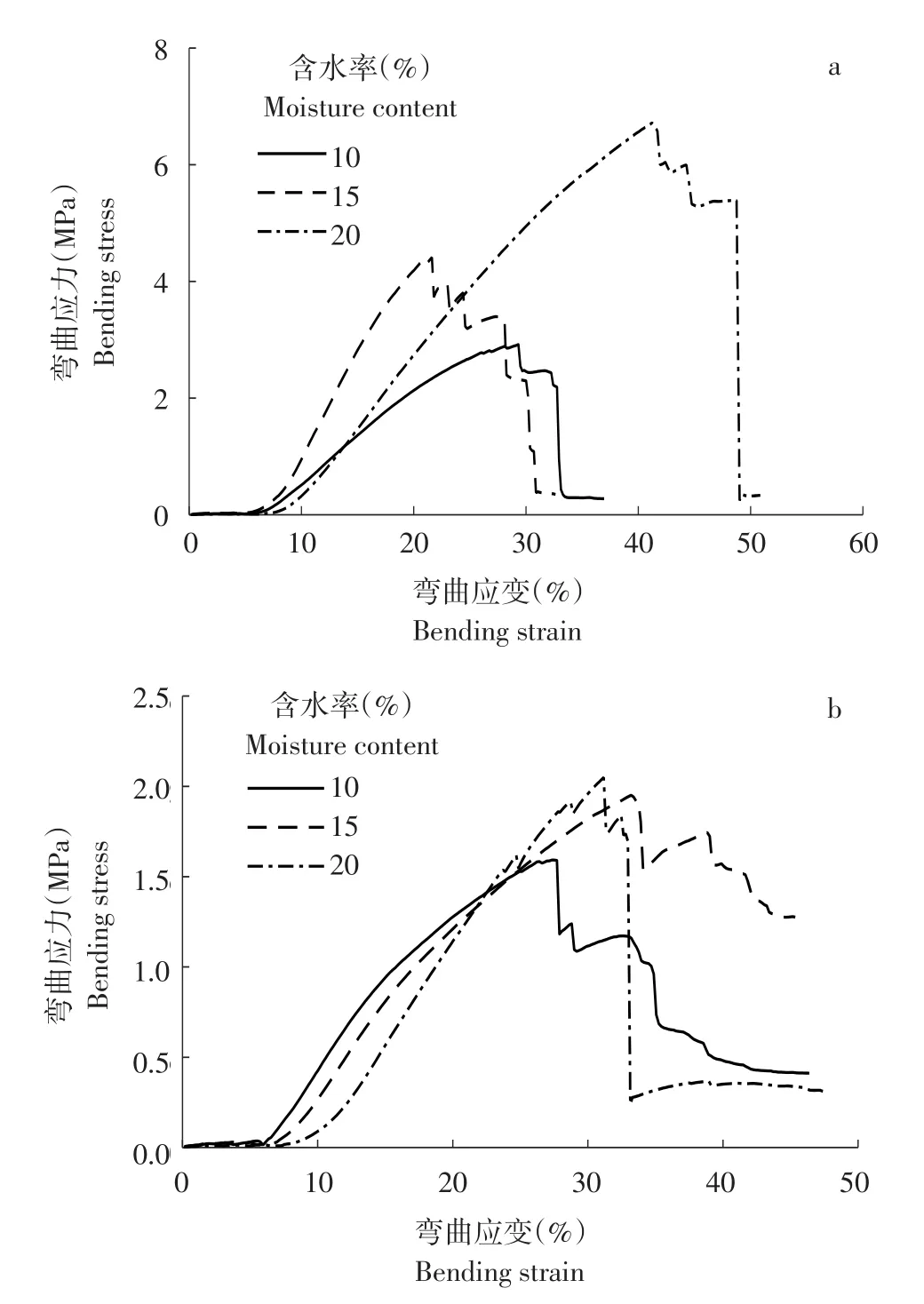
图1 通蓖7号和通蓖17号蓖麻茎秆应力-应变曲线Fig.1 Stress-strain curves of Tongbi7(a)and Tongbi17(b)castor stem

由图1可知，随弯曲应变增加，两品种蓖麻茎秆弯曲应力增大。当弯曲应变达到某一数值时，弯曲应力出现峰值，随弯曲应变继续增加，应力值开始减小，茎秆产生局部破损，直至发生断裂。随含水率增加，两品种蓖麻茎秆抗弯强度增大。说明含水率对蓖麻茎秆抗弯强度影响较大。

2 结果与分析

2.1 通蓖7号回归方程建立与显著性分析

采用三元二次回归通用旋转组合试验，结果见表2。对通蓖7号蓖麻茎秆弯曲试验抗弯强度作回归分析，求得三元二次回归方程为：

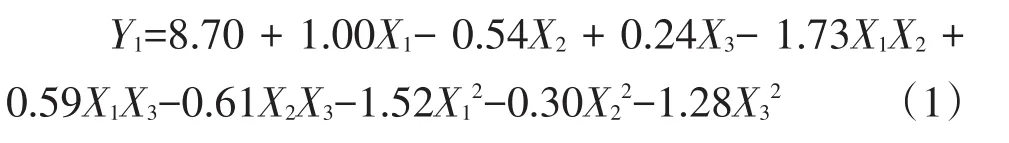
式中，Y1-抗弯强度（MPa）；X1-含水率（%）；X2-加载部位（mm）；X3-加载速率（mm·min-1）。

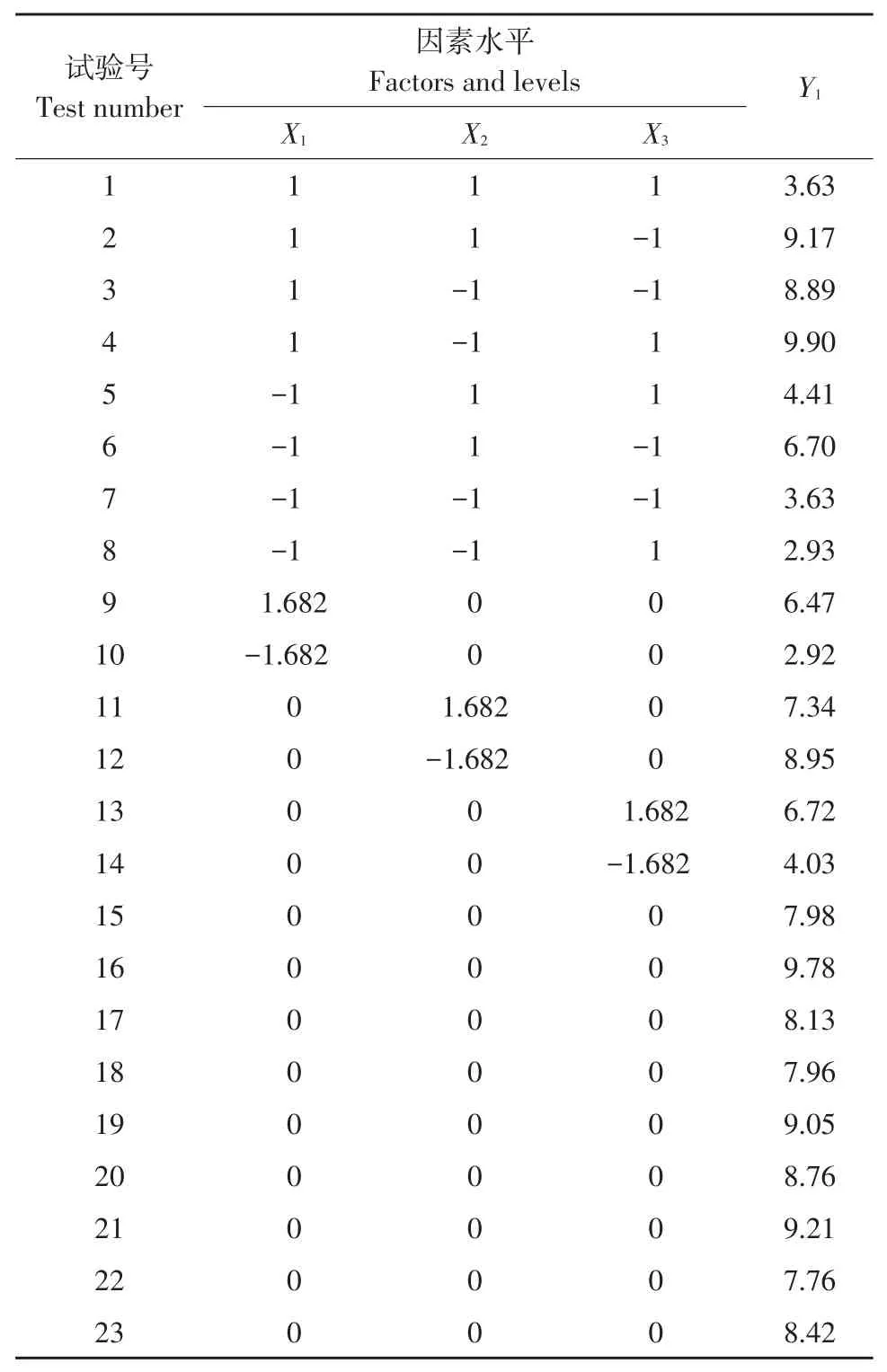
表2 三元二次通用旋转组合试验设计及结果（通蓖7号）Table 2 Experimental design and resultsof second general combination of rotating design(Tongbi 7)

为研究各试验因素对通蓖7号蓖麻茎秆抗弯强度影响程度，对回归方程作显著性检验和方差分析（显著性水平α=0.05），结果见表3。

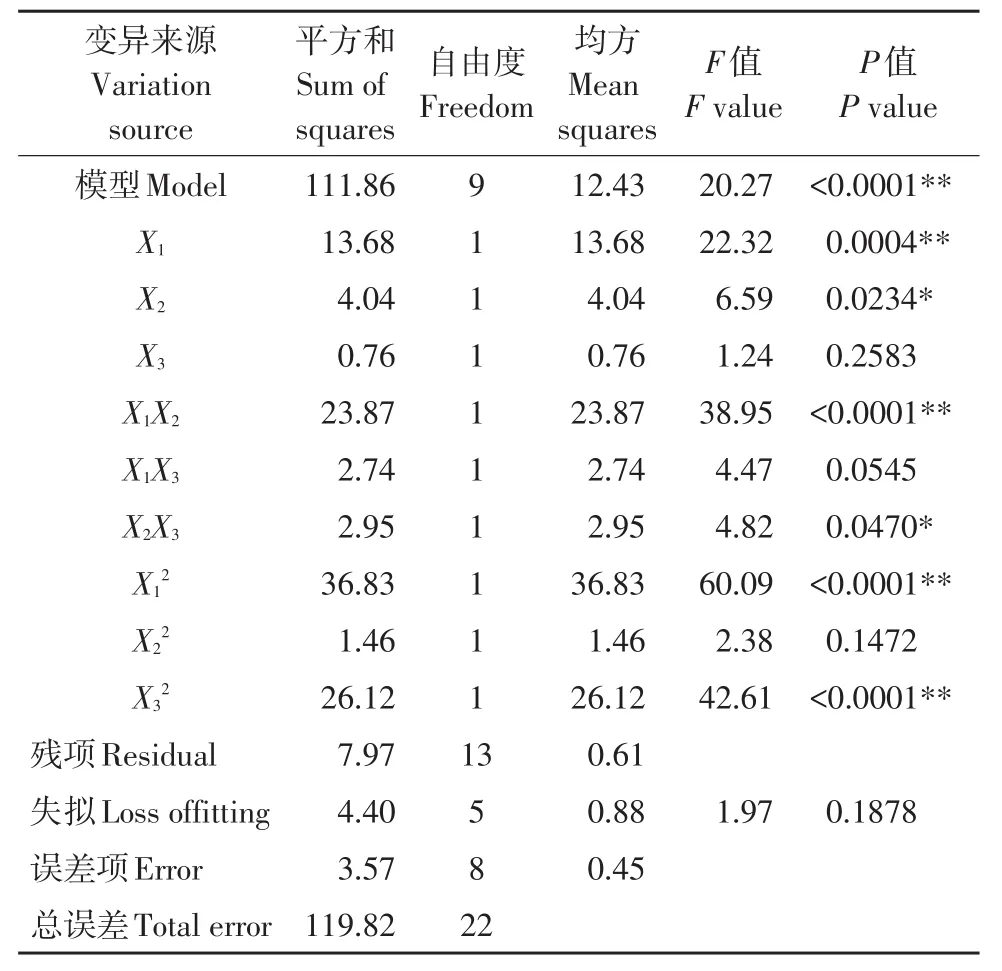
表3 弯曲试验回归方程方差分析（通蓖7号）Table 3 Varianceanalysis of bending test(Tongbi7)

由表3可知，通蓖7号蓖麻茎秆弯曲回归方程模型P＜0.0001，回归模型极显著；含水率X1对茎秆抗弯强度影响显著（P=0.0004＜0.05），失拟项P=0.1878>0.05，说明回归方程拟合较好，可用于预测各因素对抗弯强度影响。通过回归分析得出，各因素对抗弯强度影响主次顺序为：含水率>加载部位>加载速度。交互作用中，含水率与加载部位交互作用对试验指标影响极显著（P＜0.0001），加载部位和加载速度交互作用对试验指标影响显著（P=0.0470＜0.05）。剔除α=0.05不显著项，简化回归方程为：

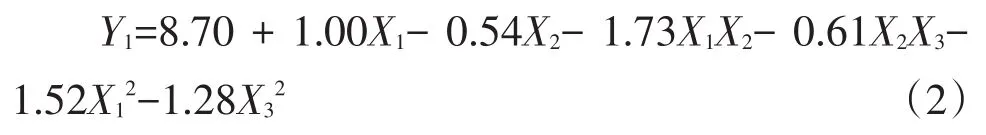
2.2 通蓖17号回归方程建立与显著性分析

采用三元二次回归通用旋转组合试验，结果见表4。对通蓖17号蓖麻茎秆弯曲试验抗弯强度回归分析，求得三元二次回归方程为：

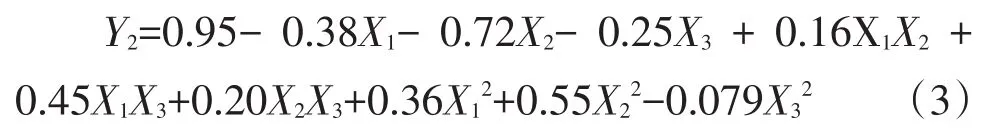
式中，Y2-抗弯强度（MPa）；X1-含水率（%）；X2-加载部位（mm）；X3-加载速率（mm·min-1）。

在α=0.05显著水平下，作显著性检验与方差分析，结果见表5。

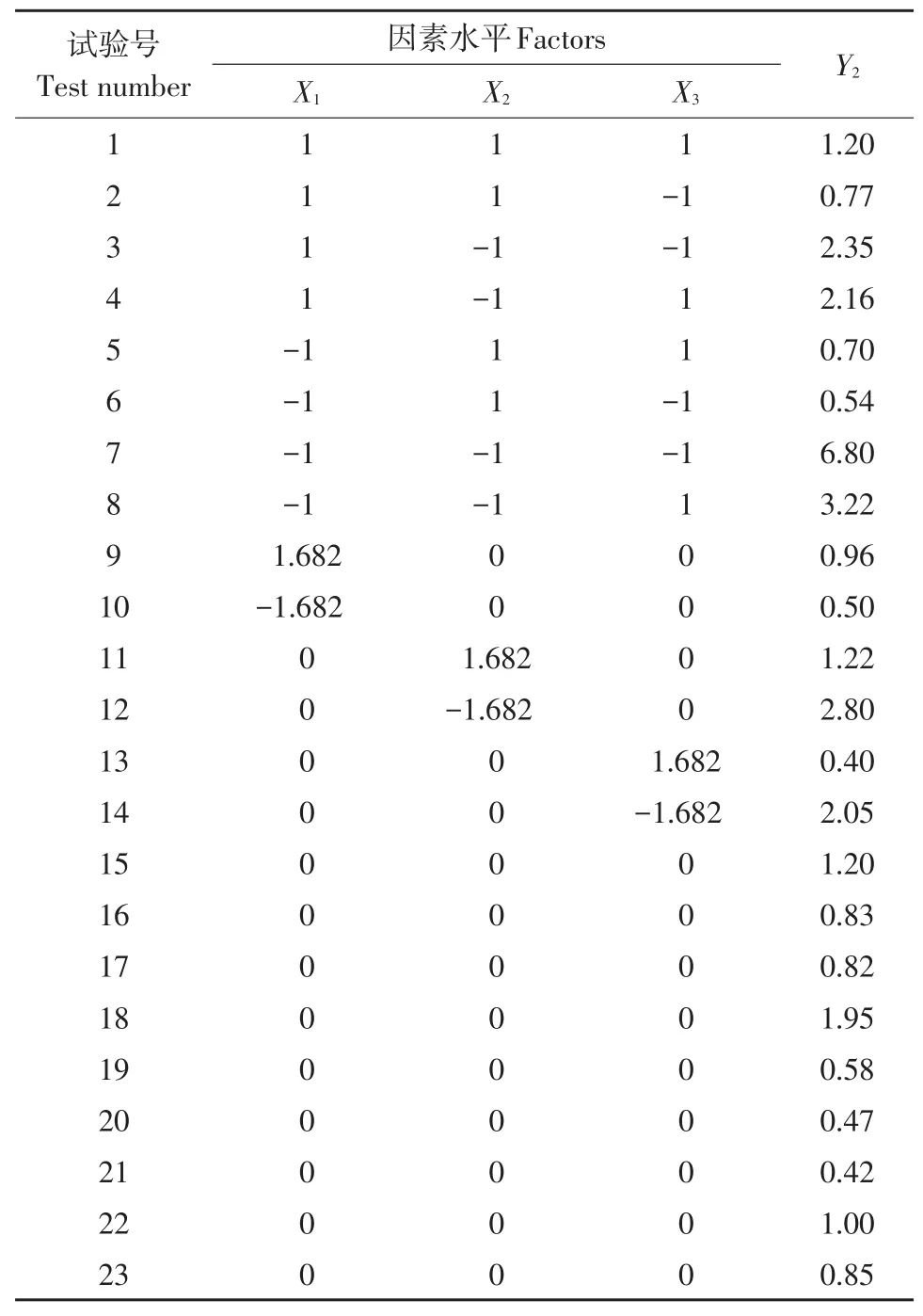
表4 三元二次通用旋转组合试验设计及结果（通蓖17号）Table4 Experimental design and resultsof second general combination of rotating design(Tongbi17)

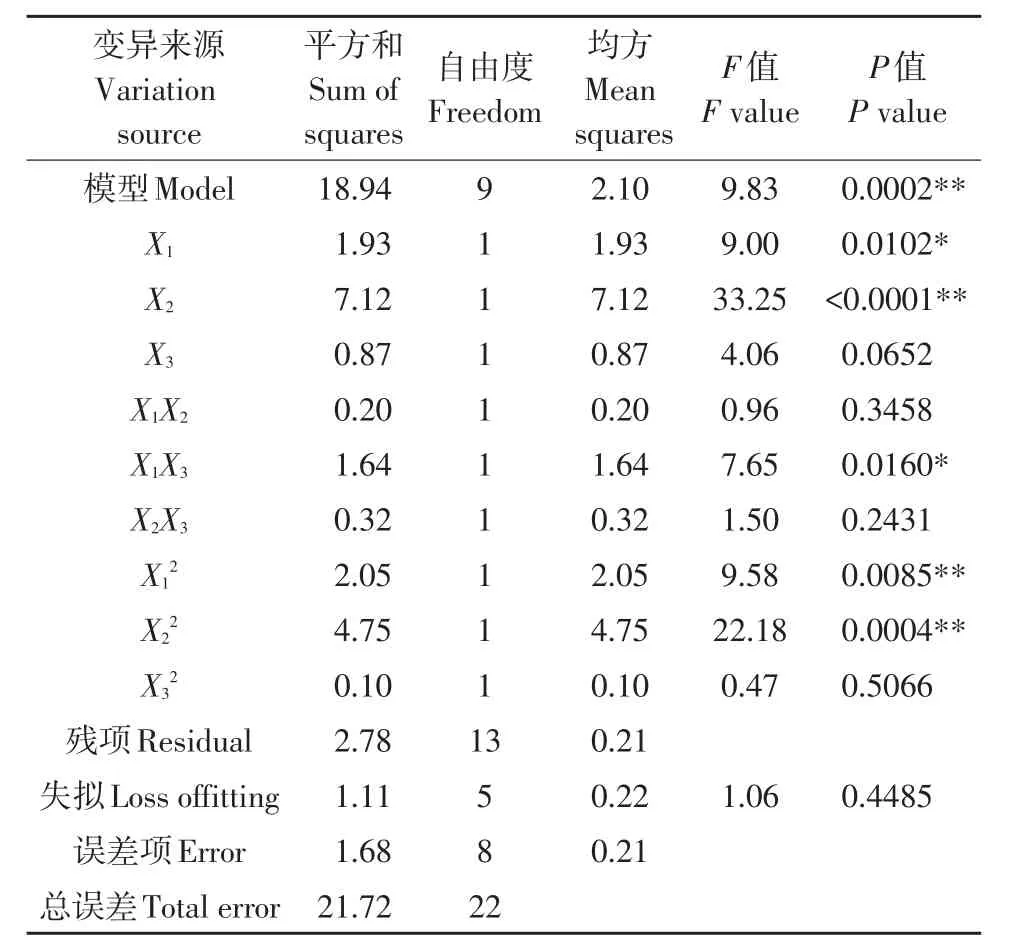
表5 弯曲试验回归方程方差分析（通蓖17号）Table5 Variance analysisof bending test(Tongbi 17)

回归方程模型P=0.0002，回归极显著；含水率对茎秆抗弯强度影响显著（P=0.0102＜0.05），加载部位对茎秆抗弯强度影响极显著（P＜0.0001）。失拟项P=0.4458>0.05，说明回归方程拟合较好，可预测各因素对抗弯强度影响。通过回归分析得出，各因素对抗弯强度影响主次顺序为：加载部位>含水率>加载速度。交互作用中，含水率与加载速度交互作用对试验指标影响显著（P=0.0160＜0.05）。剔除α=0.05不显著项，简化回归方程为：

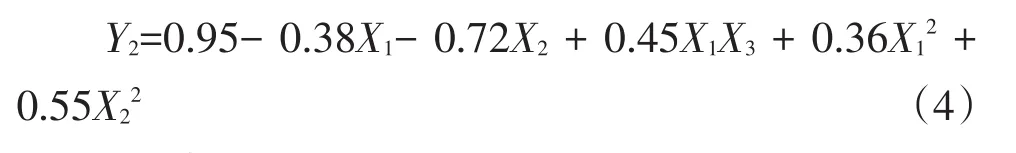
2.3 因素响应面效应分析及优化结果

各因素对通蓖7号蓖麻茎秆最大抗弯强度影响见图2，各因素对通蓖17号蓖麻茎秆最大抗弯强度影响结果见图3。

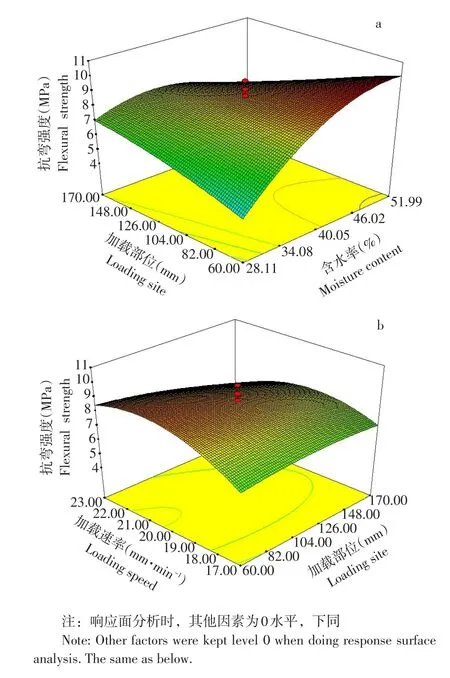
图2 各因素对通蓖7号蓖麻茎秆抗弯强度影响Fig.2 Effects of various factors on the bending strength of castor stem of Tongbi7

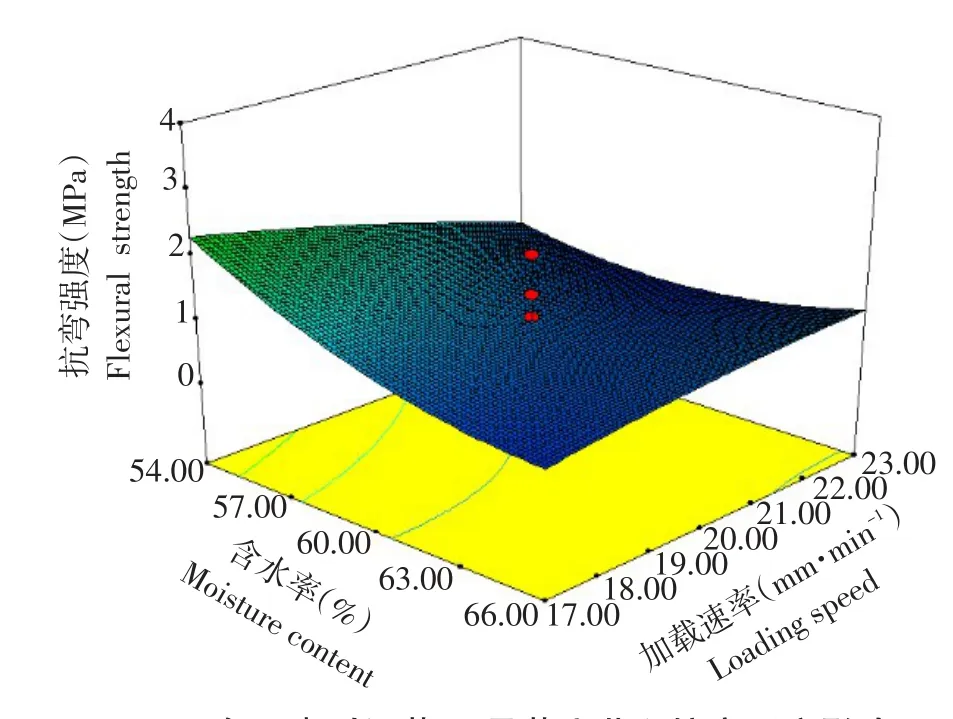
图3 各因素对通蓖17号蓖麻茎秆抗弯强度影响Fig.3 Effectsof various factorson the bending strength of castor stem of Tongbi17

由图2a可知，当加载速率为20 mm·min-1时，在不同加载部位下，抗弯强度随含水率增加呈不同变化趋势。加载部位在60～115 mm，抗弯强度随含水率增加而增加，在115～170 mm，抗弯强度随含水率增加先增后减，说明含水率与加载部位交互作用对抗弯强度影响显著（P＜0.0001）。由图2b可知，当含水率为60%时，蓖麻茎秆抗弯强度随加载速率增加呈先升后降趋势，随加载部位升高增强；说明含水率与加载部位交互作用对抗弯强度影响显著（P＜0.05）。

由图3可知，当载荷加载部位在115 mm时，蓖麻茎秆抗弯强度随含水率增加变化规律不同，加载速率17～20 mm·min-1时，抗弯强度随含水率增加而减小，加载速率20～23 mm·min-1时，随含水率增加，抗弯强度先减后增，说明含水率和加载部位交互作用，对蓖麻茎秆抗弯强度影响显著（P＜0.05）。

以茎秆抗弯强度为响应值，利用Design export 8.0.6软件设定茎秆抗弯强度目标值为Minimum，得到茎秆最小抗弯强度预测值及各影响因素见表6，研究结果可为设计切割装置提供参考。

表6 抗弯强度最小时各因素组合Table6 Combination of factorswhen the bending strength is minimized

3 纤维导管含量计算

3.1 蓖麻茎秆结构

蓖麻茎秆主要由秆皮部、木质部、髓部和纤维导管组成[16]。通蓖7号蓖麻茎杆各节中部截面见图4。

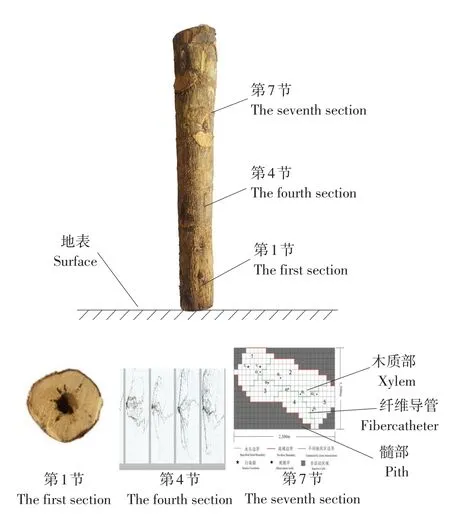
图4 蓖麻茎秆截面Fig.4 castor stem section

由图4可知，不同生长高度蓖麻茎秆内部结构差异较大，各节纤维导管含量分布不均。靠近地表处第1节茎秆木质部较厚，无明显髓部和纤维导管。第4节处有一定数量纤维导管且分层状明显，第7节处木质部与第4节相比无差异，但纤维导管数量明显多于第4节。说明不同生长高度对应纤维导管含量影响蓖麻茎秆抗弯强度。

3.2 单束纤维导管截面积

采用VHX-5000超景深显微镜放大20倍条件下拍摄茎秆截面见图5。单束纤维导管可近似为圆柱体，利用VHX-5000测量功能测得各节纤维导管直径均值，计算导管截面积。由图6可知，通蓖7号蓖麻茎秆在接近地表1～3节处，单束纤维导管截面积随高度增加而减小。3～5节处通蓖7号单束纤维导管截面积增加趋势明显，且在第5节处出现最大值。

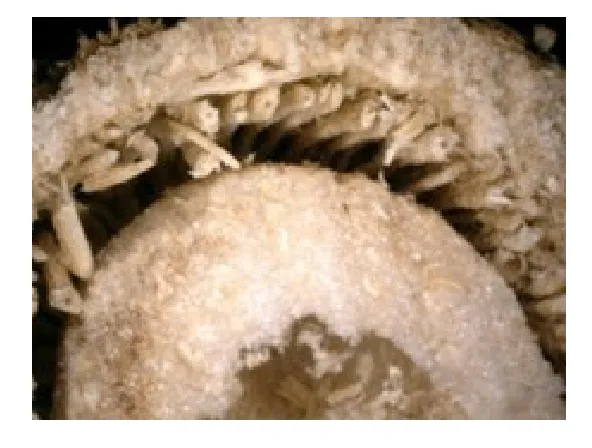
图5 蓖麻茎秆显微截面Fig.5 Castor stem micro section

图6 单束纤维导管截面积分布规律Fig.6 Distribution ruleof cross-sectional area of fiber conduit

3.3 导管-茎秆体积比

为研究纤维导管含量沿蓖麻茎秆生长方向变化规律，采用导管-茎秆体积比作为衡量各节纤维导管含量标准。由蓖麻茎秆截面显微结构统计5根通蓖7号蓖麻茎秆各节纤维导管，取均值。根据单束纤维导管截面积即可计算各节纤维导管面积。各节纤维导管平均数量分布见图7，可见各节纤维导管数量差异较大。通蓖7号纤维导管-茎秆体积比随生长高度变化见图8。

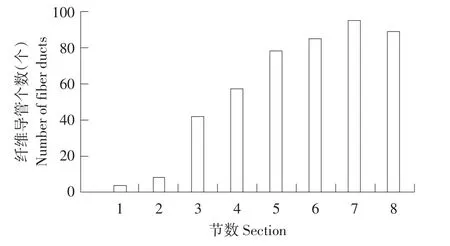
图7 纤维导管数量分布Fig.7 Distribution number of fiber ducts

图8 导管-茎秆体积比随高度变化规律Fig.8 Density ratio of catheter to stem varies with height

由图8可知，导管-茎秆体积比随生长高度变化规律近似为二次函数，通蓖7号纤维导管含量随生长高度增加而增加。导管-茎秆体积比与生长高度定量关系为：

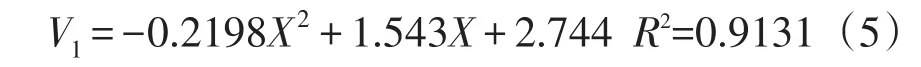
式中，V1-通蓖7号纤维导管含量（%）；X-生长高度（mm）。

4 有限元仿真

为探讨导管纤维体积比对茎秆抗弯强度影响，本文用有限元法对3种不同导管-茎秆体积比（3%、4%、5%）通蓖7号蓖麻茎秆作弯曲试验仿真分析。有限元分析过程中相关假设：①忽略秆皮部影响，蓖麻茎秆近似为圆柱体。②蓖麻茎秆各部分材料简化为：轴向同性，径向异性。③仿真时各部位导管-茎秆体积比一致。④施加载荷前，蓖麻茎秆内部应力为零，且在仿真过程中，含水率和温度无变化。

4.1 几何模型建立

建立蓖麻茎秆几何模型时，将其简化为由木质部、纤维、髓部3部分组成圆柱体。采用游标卡尺（精度0.02 mm）测量10株通蓖7号蓖麻茎秆（取均值）：主茎长度232 mm、直径26 mm、髓部内腔直径3 mm，髓部壁厚9 mm。根据已测茎秆主要尺寸参数，采用三维设计软件Solidworks创建蓖麻茎秆三维实体模型，如图9所示。

4.2 网格划分及材料属性

网格划分时，单元类型选取Solid186，采用自由划分网格方法，网格精度设置2 mm。划分网格之后模型见图10。

图10 蓖麻茎秆模型网格划分Fig.10 Castor stem model grid division

3点弯曲试验测得蓖麻茎秆各部分弹性模量。测量纤维导管弹性模量时将茎秆杆皮部剥离，测量髓部弹性模量时将附着在秆皮内表面上纤维导管剥离。

采用引伸计测得各部分在单向受压状态下横向应变与轴向应变，由公式（6）确定各部分泊松比。

式中，σ-泊松比；ε1-横向应变；ε2-轴向应变。

采用真实密度测试原理，通过试验测得蓖麻茎秆真实密度0.18 g·cm-1。

各部分材料属性见表7，将表中材料参数输入对应模型。

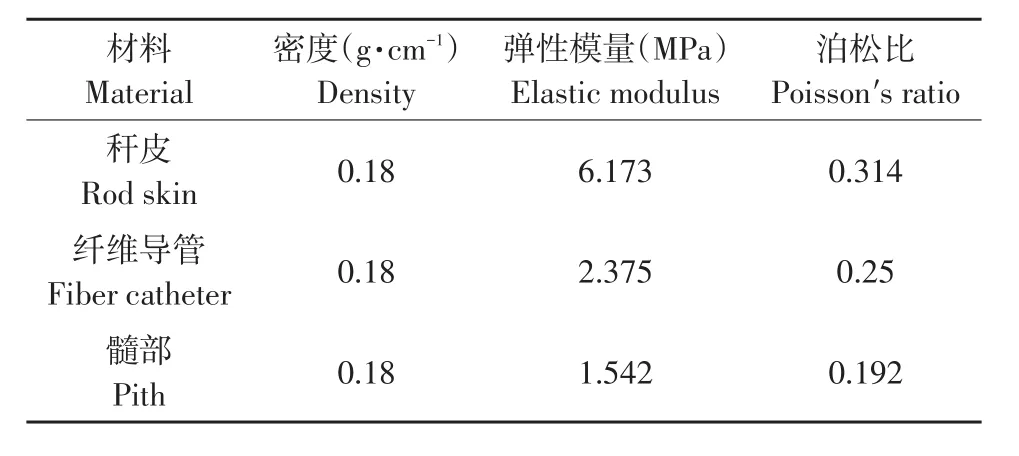
表7 茎杆各部分材料参数Table7 Stem partsmaterial parameters

4.3 边界条件设置

为模拟真实3点弯曲试验过程，在蓖麻茎秆几何模型上下位置，分别创建压块与下支撑块，下支撑块与茎秆接触，压块与茎秆之间保持一段距离。压块施加垂直向下速度，其值与茎秆弯曲试验时WDW-2型微机控制电子万能试验机加载速度一致，下支撑添加固定约束。

4.4 仿真结果与分析

根据所建3种不同导管-茎秆体积比蓖麻茎秆有限元模型，利用ANSYS中Explicit Dynamics显示动力学分析模块[17]分析求解，得到3种不同体积比下蓖麻茎秆弯曲应力云图，如图11所示。

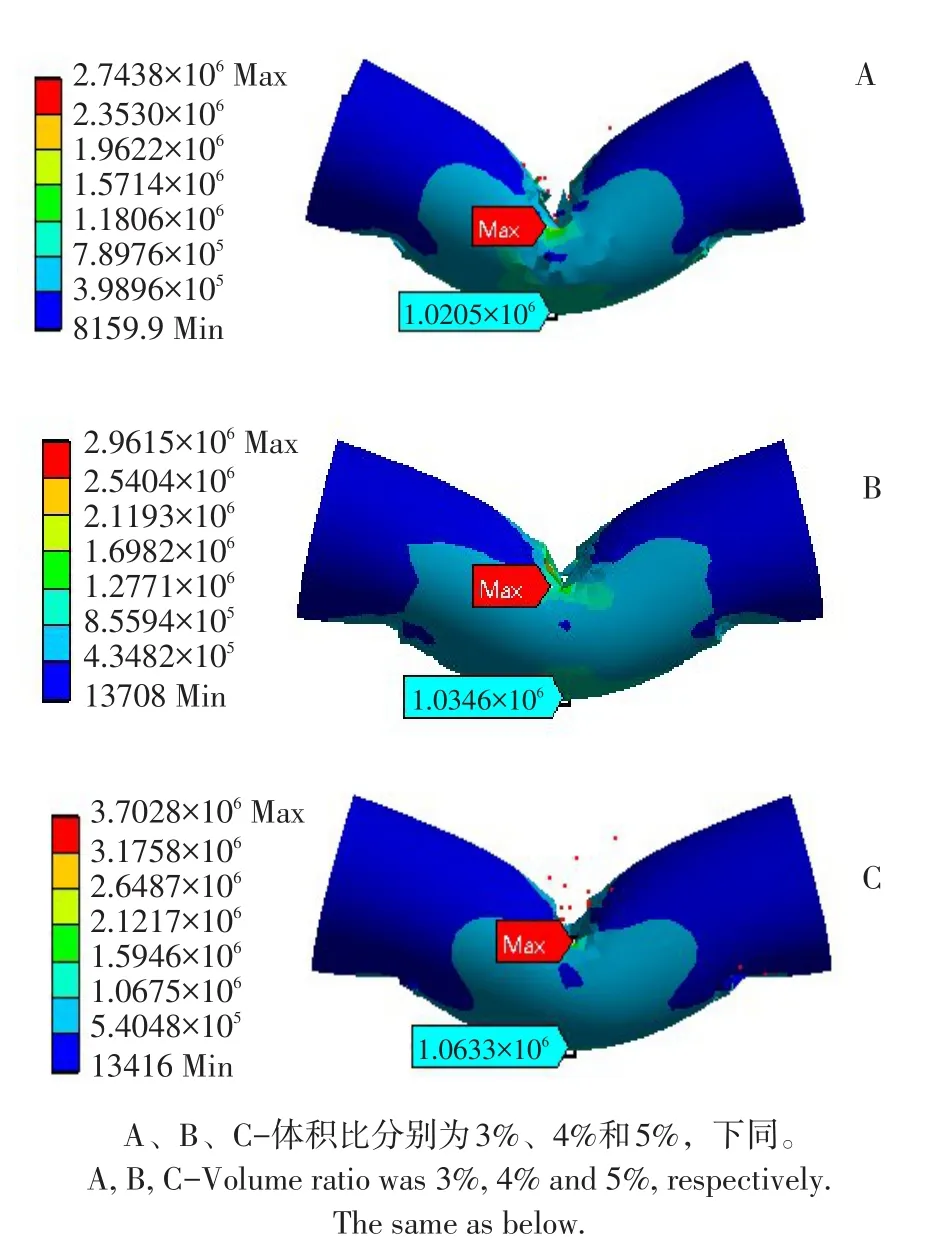
图11 蓖麻茎秆弯曲时应力云图Fig.11 Equivalent stress map of castor stems when bent

由图11可知，3种不同纤维导管含量条件下茎秆应力分布规律基本一致：以压块与茎秆接触位置处为中心，应力向四周扩散且逐渐减小，在压块与茎秆接触处附近出现应力峰值，最大值分别为2.7438 MPa（体积比3%）、2.9615 MPa（体积比4%）和3.7028 MPa（体积比5%）。且3种体积比条件下，茎秆最大位移处应力分别为1.0205 MPa（体积比3%）、1.0346 MPa（体积比4%）和1.0633 MPa（体积比4%），说明随纤维导管含量增加，茎秆抵抗变形能力增强，破坏时越不易产生裂纹。

压块与茎秆接触损伤区域见图12。从茎秆受损坏形式上看，在压块与茎秆持续接触过程中，接触区域网格质量急剧下降，此时茎秆破裂，茎秆损伤由接触区域向四周扩展。随导管-茎秆体积比增加，损伤面积减小。说明随导管纤维含量增加，导管对茎秆支撑作用逐渐增强，茎秆抗弯强度增加，不易损坏。

图12 不同体积比茎秆损伤规律Fig.12 Different volume ratios of stem damage

4.5 体积比及对应加载部位与抗弯强度关系

选取3%～4.8%体积比对应加载部位试样，通过试验得到加载部位对抗弯强度影响拟合曲线，并对比有限元仿真结果，如图13所示。导管-茎秆体积比与茎秆抗弯强度呈非线性递增关系，当体积比3%～4%时，抗弯强度增加速率较缓慢，当体积比大于4%时，递增趋势显著加快。

采用最小二乘法拟合数据，得到抗弯强度与体积比拟合方程为：

式中，y-茎秆抗弯强度（MPa），x-纤维导管含量（%）。

两变量间相关程度可由式（8）确定，其值介于-1与1之间，当R值越接近1时，说明两变量间相关程度越大[18]。

式中，R-相关系数；Y1-试验结果；Y2-仿真结果。

计算得两曲线相关系数R=0.9014，仿真结果与试验结果呈正相关，说明载荷加载部位对茎秆抗弯强度影响由加载部位点茎秆内部纤维导管含量决定。

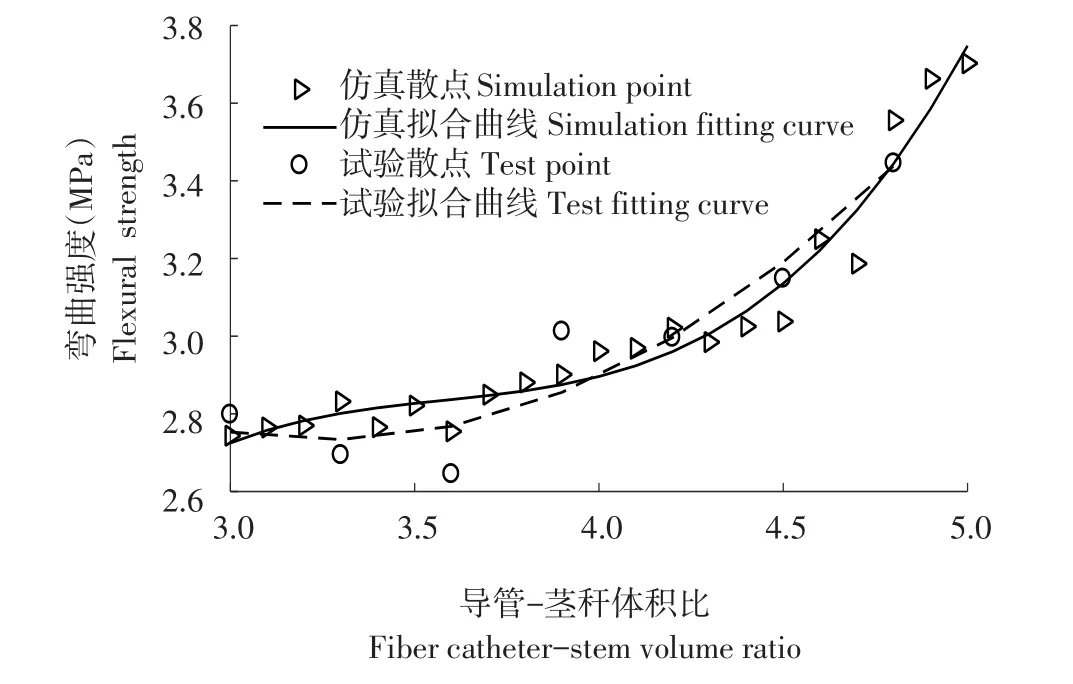
图13 体积比与抗弯强度拟合曲线Fig.13 Volumeratio and bending strength curve

5 讨论与结论

a.试验结果表明，各因素对通蓖7号蓖麻茎秆抗弯强度影响排序为：含水率>加载部位>加载速度。其中，含水率与加载部位交互作用对试验指标影响极显著（P＜0.0001），加载部位和加载速度交互作用对试验指标影响显著（P=0.0470＜0.05）。各因素对通蓖17号蓖麻茎秆抗弯强度影响主次顺序为：加载部位>含水率>加载速度。其中，含水率与加载速度交互作用对试验指标影响显著（P=0.0160＜0.05）。

b.利用Design export 8.0.6软件优化程序分别得出两品种茎秆抗弯强度最小时最佳因素组合：当通蓖7号含水率为59.25%，加载部位为92.03 mm，加载速度为15.56 mm·min-1时，抗弯强度最小，为2.774 MPa；当通蓖17号含水率为55.97%，加载部位为150.94 mm，加载速度为24.54 mm·min-1时，抗弯强度最小，为0.229 MPa。试验结果可为蓖麻收获机械切割装置设计提供参考。

c.以通蓖7号蓖麻茎秆为对象，通过研究茎秆微观结构，分析不同生长部位茎秆内部纤维导管含量变化规律。借助有限元软件分别得出纤维导管含量和加载部位对抗弯强度影响拟合曲线，两曲线相关系数R=0.9014。研究表明，加载部位对抗弯强度影响实际上取决于该部位纤维导管含量。