不同替代模型在地下水污染源释放历史反演中适用性研究
邢贞相,曲睿卓,赵 莹,纪 毅,张 涵
(1.东北农业大学水利与土木工程学院,哈尔滨 150030;2.农业部农业水资源高效利用重点实验室,哈尔滨 150030)
随着城镇化建设和经济快速发展,地下水污染日益严重。地下水系统复杂,污染源信息不易获取[1],难以在源头治理地下水污染,治理成本高、难度大[2],治理修复措施无法完全发挥作用[3]。因此,降低地下水污染风险,识别地下水污染源特征成为当前研究重点。Bagtzoglou和Atmadja运用直接水文反演方法,重建保守污染羽空间分布[4]。Alapati和Kabala使用非线性最小二乘法识别地下水污染物羽流释放历史[5]。优化算法是解决地下水反演问题最普遍且高效的方法[6-7]。优化算法分为局部优化算法[8]和启发式算法[9]。相对于局部优化算法,启发式算法不会陷入局部极小值,可解决非凸模型优化问题,广泛应用于地下水污染源识别[10]。遗传算法(Genetic algorithm,GA)是最常见启发式算法,应用于解决二维含水层中污染源反演问题,可提高模型计算效率[11]。利用GMS软件中MODFLOW和MT3D两个模块可建立地下水污染运移过程模拟模型,将优化模型与模拟模型结合,通过反演求得污染源释放过程。遗传算法可提高计算效率,但反演过程反复调用模拟模型,耗时较长,适用性较弱。替代模型计算时间短,功能与模拟模型相似。替代模型研究中,曾主要以人工神经网络(Artificial neural network,ANN)为主[12]。Zhao等研究发现克里格(Kriging)模型在相同地质条件下,反演速度和准确性均优于ANN[13]。其他替代模型包括双响应面法[14]、BP神经网络模型[15]、径向基函数神经网络(RBF)[16]、支持向量机法(SVM)[17]等。
替代模型是解决地下水污染源反演有效方法,但不同替代模型对水文地质条件区域适用性不同。因此,本文选用Kriging、广义回归神经网络(GRNN)和最小二乘支持向量机法(LSSVM)3种应用较广泛替代模型,对比分析不同复杂水文地质条件下其对地下水污染源释放历史反演适用性。目前Kriging和RBF替代模型较广泛。但RBF替代模型存在难以确定隐层节点等问题且适用性一般,故选用GRNN替代模型。GRNN替代模型在学习速率与逼近能力方面明显优于RBF替代模型[18]。选择LSSVM作为替代模型速度更快、精确度更高[19]。为探究3种替代模型适用性,将选择相同输入输出训练模型,从模型学习能力和反演时间、准确性和稳定性等方面评价。
1 研究方法
1.1 克里格(Kriging)
Kriging模型是依据协方差函数对随机过程空间建模和预测回归的算法[20]。其基本形式为:

其中x代表输入数据,y(x)代表模型输出,g(x)代表原始函数全局模型,Z(x)代表高斯随机函数。Z(x)协方差可计算如下:
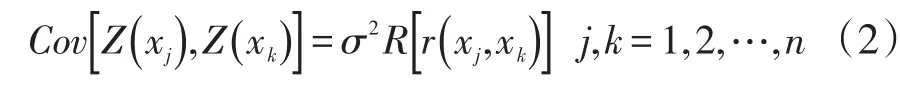
其中R代表相关函数,r代表对称相关矩阵,n代表样本数。

1.2 广义回归神经网络(GRNN)
广义回归神经网络具有很强非线性拟合能力和柔性网络结构[21],GRNN模型由输入层、模式层、求和层和输出层组成。输入层神经元数目等于学习样本中输入向量维数。模式层为隐含层,其神经元数目等于样本数n,神经元i传递函数为:
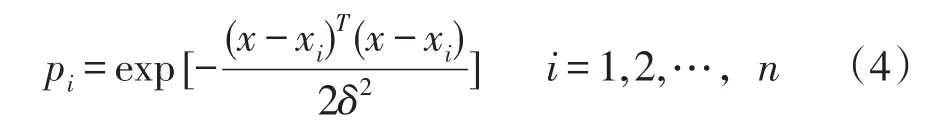
式中,xi为各单元核函数中心向量。
在求和层中,计算模式层各单元输出之和与模式层各单元输出加权,其传递函数分别为:

式中,yi为各训练样本加权和权重值;最后由输出层计算输出,输出层神经元数目等于样本中输出向量维数[22],公式为:

1.3 最小二乘支持向量机(LSSVM)
LSSVM用于解决模式分类和函数估计问题,通过计算样本最小平方误差拟合。其功能描述如下[23]:

训练样本集是{( xi,yi)|i=1,2,…,n} ,xi是输入变量值,yi是对应输出变量。其中x是输入向量,ω是权重向量,d是偏差,φ是高维特征空间映射。根据结构风险最小化原则,寻求ω最小化方程为:

其中γ是惩罚因子,ei是误差控制函数。将约束条件在方程式(8)中给出:
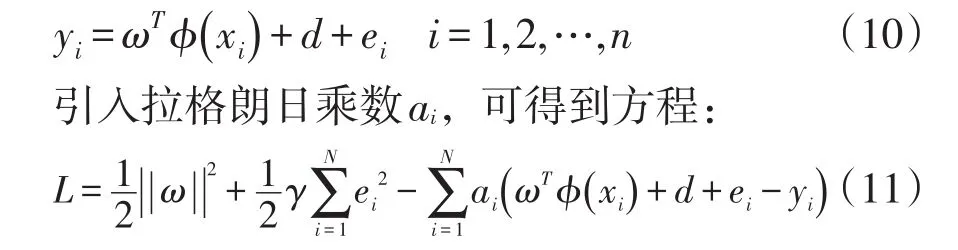
根据(Karush-Kuhn-Tucker)KKT条件,LSSVM方程两边偏导数为:
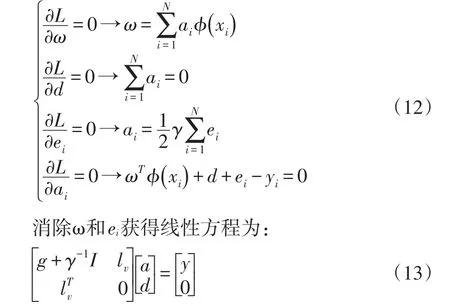
式中,y=[y1,y2, …,yn]T,a=[a1,a2, …,an]T,lv=[1,1,...,1]T,I为单位矩阵,g为相邻矩阵。g(xi,xj)=φ(xi)Tφ(xj),i,j=1,…,n,为满足Mercer理论核矩阵[24]。径向基函数具有广泛收敛域和强泛化能力,为理想回归核函数。可表示如下:
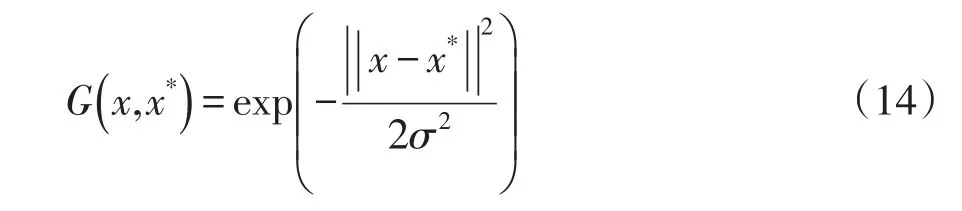
式中,σ-核宽度参数,影响LSSVM在特征空间中获得最优分类超平面泛化能力。LSSVM预测模型可表示为:

1.4 评价指标
为验证替代模型精度,采用确定性系数(R2)、相对误差(RE)和均方根误差(RMSE)3种精度评估指标。R2越接近1,表示模型拟合精度越高。RE和RMSE越接近0,表示模型精度拟合精度越高。其公式如下:
①确定性系数(Coefficient of determination,R2)

式中,yi为模拟模型输出值,即真实观测浓度值;yˆi为替代模型输出值;yˉi为模拟模型输出值平均值。
②相对误差(Relativeerror,RE)

2 地下水流数值模拟模型建立
2.1 替代模型建立
利用拉丁超立方抽样方法对模型输入抽样,即为地下水污染源释放浓度。本文研究3种不同水文地质条件案例分别有500组输入数据。分别输入GMS模拟模型中,得到500组输出值,即得到观测井观测浓度值。将其中相同450组输入和输出作为3个替代模型训练样本,利用剩余50组输入和输出数据作为检验组验证替代模型精度。
2.2 替代模型验证
3种替代模型不同情况下模拟表现存在差别,不同案例情况下3种替代模型得到训练,验证模型精度,分析模型学习能力。结果见表1和2。
确定性系数反映模型预测值与实际观测值拟合度,其可检验替代模型模拟能力,但无法检验预测极值能力。而相对误差对模拟值中极大或极小值误差反映敏感。通过模拟3个案例观测值发现,3种替代模型R2均在0.9以上,RE均在20%以内。说明建立这3种替代模型有效,可运用于后续反演。对比发现,GRNN替代模型学习能力较弱,但表现较稳定,在案例1和案例2条件下R2和RE较接近。在案例3情况下,模拟精度下降。Kriging替代模型学习能力较强,R2均在0.99以上,但对于极小值和位置较远观测井观测值模拟能力较弱。在案例3中,第6、7观测井位置RE高于其他口井位置。LSSVM替代模型在水文地质较为简单情况下,预测能力较强,随水文地质条件变化,R2降低,RE增高。通过案例1和案例3对比可知,LSSVM在复杂水文地质条件适用性较差。
2.3 地下水污染源识别模型建立
完成Kriging、LSSVM和GRNN替代模型建立后,将其替代模拟模型与优化模型结合,反演地下水污染源释放过程。运用Matlab中GA优化工具箱求解未知参数,种群数为20,迭代200次达到收敛。当观测数据存在噪声时,优化过程增加至迭代500次。
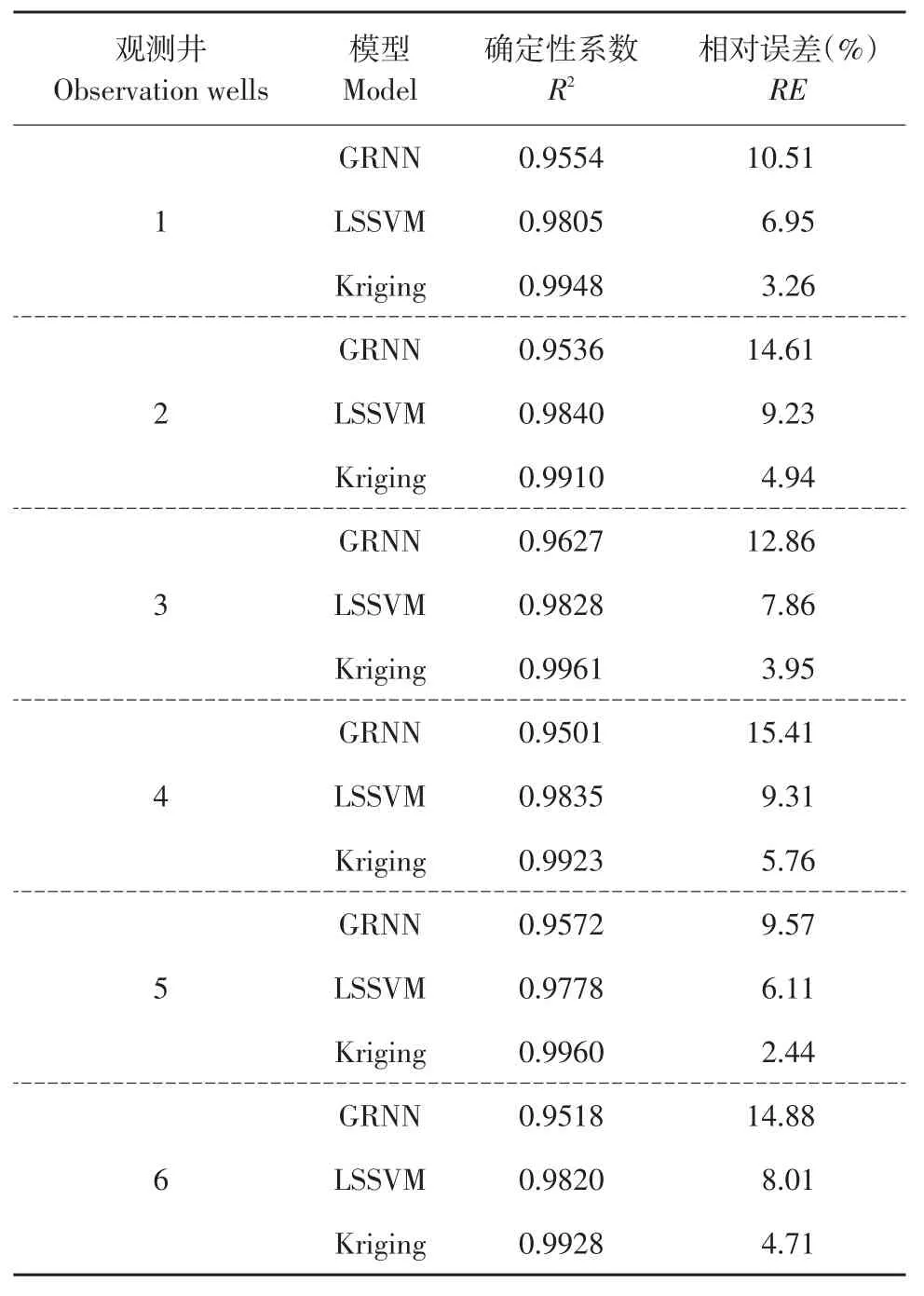
表1 替代模型在案例1中模拟结果Table1 Simulation resultsof surrogatemodelsin case 1
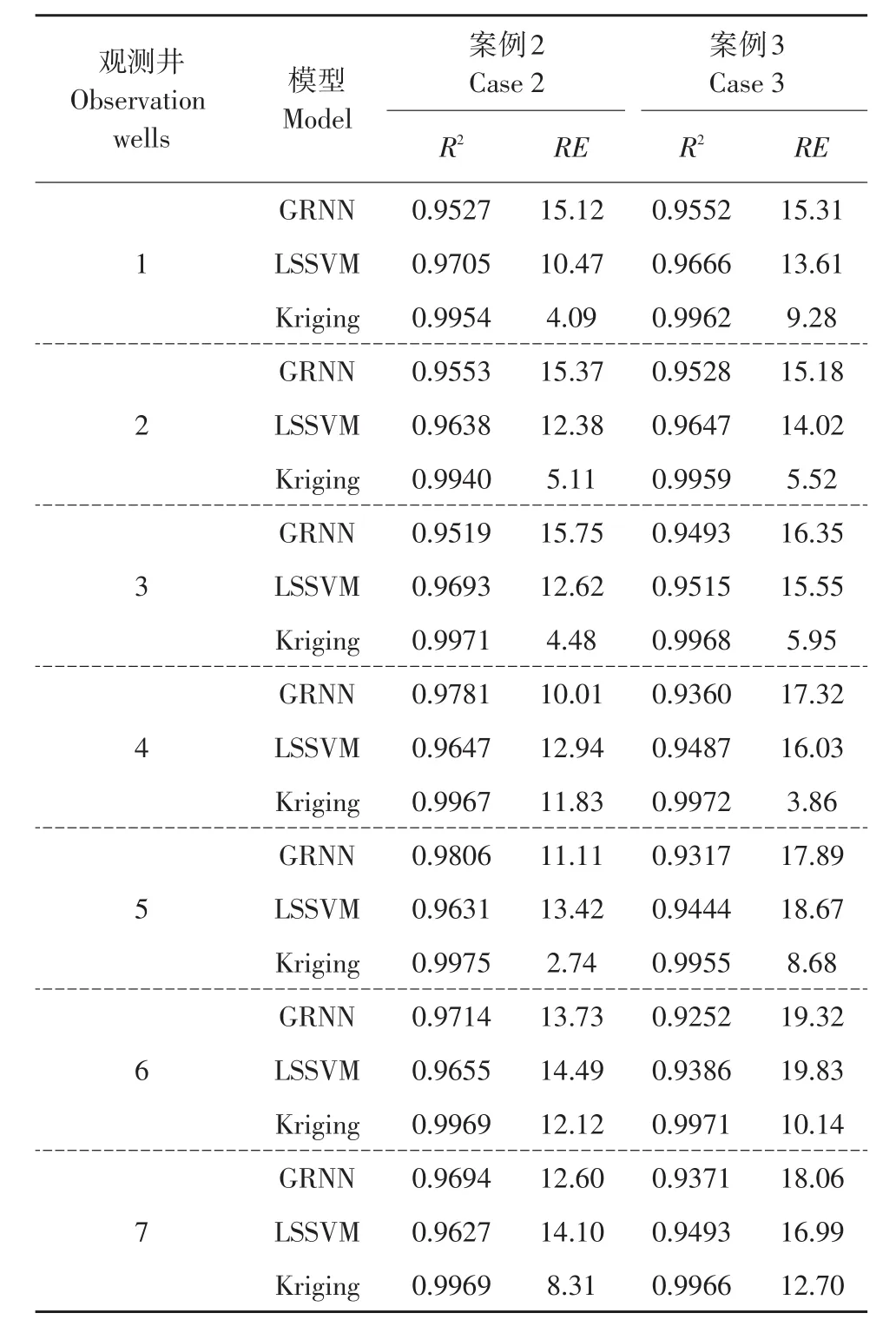
表2 替代模型在案例2和案例3中模拟结果Table 2 Simulation resultsof surrogate modelsin case 2 and case3
2.4 测量误差
由于野外和实验室研究均可能存在测量误差,观察浓度具有不确定性。因此,实际浓度如下式:

其中C为观测污染物浓度。ε是误差矩阵,表示数据中存在噪声水平。如果a<0.10,则噪声水平低。如果0.10≤a≤0.15,则噪声水平适中。如果a>0.15,则噪声水平高。
3 案例分析
3.1 二维规则边界稳流均质含水层(案例1)
本研究通过3种不同水文地质条件案例,测试反演模型性能。第1种水文地质研究区域平面图见图1。

图1 案例1含水层结构平面Fig.1 Aquifer structureplane of case 1
含水层模型边界条件是东侧和西侧特定水头线性变化,北侧和南侧无流动。该含水层有3个污染源和4个采样点,每个采样点采集污染浓度。模拟时间为5年(60个月),分为20个相等压力期,每个压力期持续3个月。假设源在前4个压力期间释放污染物。表3列出实际污染源释放浓度。根据上述建立模拟-优化模型对案例1作地下水污染源释放过程反演,得到结果见图2,误差分析结果见表4。
由图2可知,3种替代模型反演结果与真实地下水污染源释放浓度较接近。R2均在0.99以上,RE均在5%以内,RMSE均为1.5。说明案例1水文地质情况下,3种替代模型反演精度较高,适用性较好。

表3 案例1地下水污染源流量实际值Table 3 Actual value of groundwater pollution sourceflux in Case 1
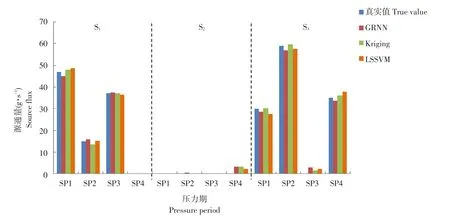
图2 不同替代模型对案例1污染源释放历史反演结果Fig.2 Retrieval results of different surrogatemodels on the release history of case 1 pollution sources

表4 案例1反演结果误差Table 4 Retrieval result error in case 1
3.2 二维非规则边界非均质稳流含水层(案例2)
案例2研究区域是几何不规则形状,含水层不均匀,平面图见图3。该含水层有5个不同水力传导带,每个区域水力传导率值恒定。水力传导率值为:K1=0.0004 m·s-1,K2=0.0002 m·s-1,K3=0.0001 m·s-1,K4=0.0003 m·s-1,K5=0.0007 m·s-1s。
该含水层有2个污染源和7个取样点。模拟时间为10年(120个月),且分为20个相等压力期,每个应力期持续6个月。假设源在前4个应力期释放污染物。
表5列出实际污染源释放浓度。反演结果见图4,误差分析结果见表6。

图3 案例2含水层结构平面Fig.3 Aquifer structure plane of case 2

表5 案例2地下水污染源流量实际值Table 5 Actual value of groundwater pollution source flow in case 2
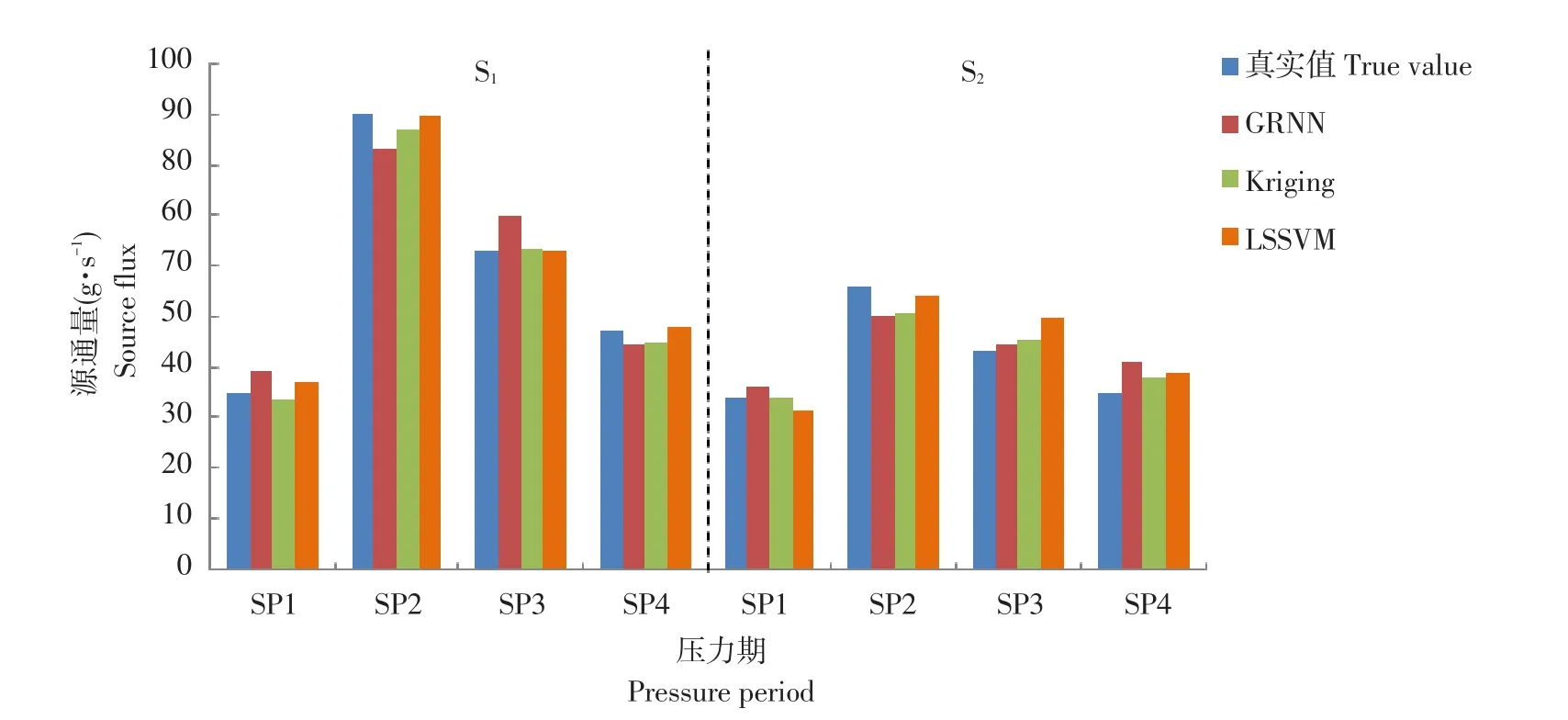
图4 不同替代模型对案例2污染源释放历史反演结果Fig.4 Retrieval results of different surrogate models on the release history of case 2 pollution sources
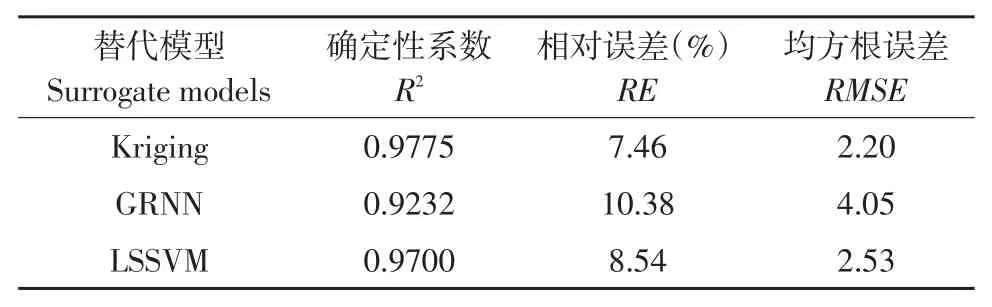
表6 案例2反演结果误差Table6 Retrieval result error in case 2
由表6可知,在案例2较复杂含水层条件下,Kriging和LSSVM替代模型表现较稳定。与案例1相比,Kriging和LSSVM替代模型R2下降0.02%,RMSE升至2.20,RE均小于10%,表明两种模型对案例2含水层条件适用性较好。而GRNN替代模型RE和RMSE均较高,且R2下降0.07%。虽然反演结果在合理范围内,但相较于其他两种模型,反演结果误差较大。
3.3 二维非规则边界非稳流非均质含水层(案例3)
由图5可知,含水层其他特征与第2种情况相同。与案例2不同的是,1个抽水井存在于地质层中心,模拟地下水水流瞬态流动和瞬态传输条件。所需反演实际值与案例2相同。反演结果如图6所示,误差分析结果如表7所示。
由图6和表7可知,Kriging替代模型反演结果较其他2种替代模型更优,R2接近0.99,RE在10%以内且RMSE为2.8。运用LSSVM替代模型反演结果不如Kriging替代模型,但相较于案例2,表现较稳定。其RE在10%以内,RMSE在5以内,说明在案例3情况下,LSSVM替代模型适用性较好。运用GRNN替代模型反演结果精度较低,R2小于0.9,RMSE为6.62,RE高达20%以上,误差较大。说明GRNN替代模型对于案例3水文地质情况适用性较差。
为进一步检验3种替代模型结合优化模型对地下水污染源释放历史反演适用性和稳定性,反演结果和误差分析见图7。
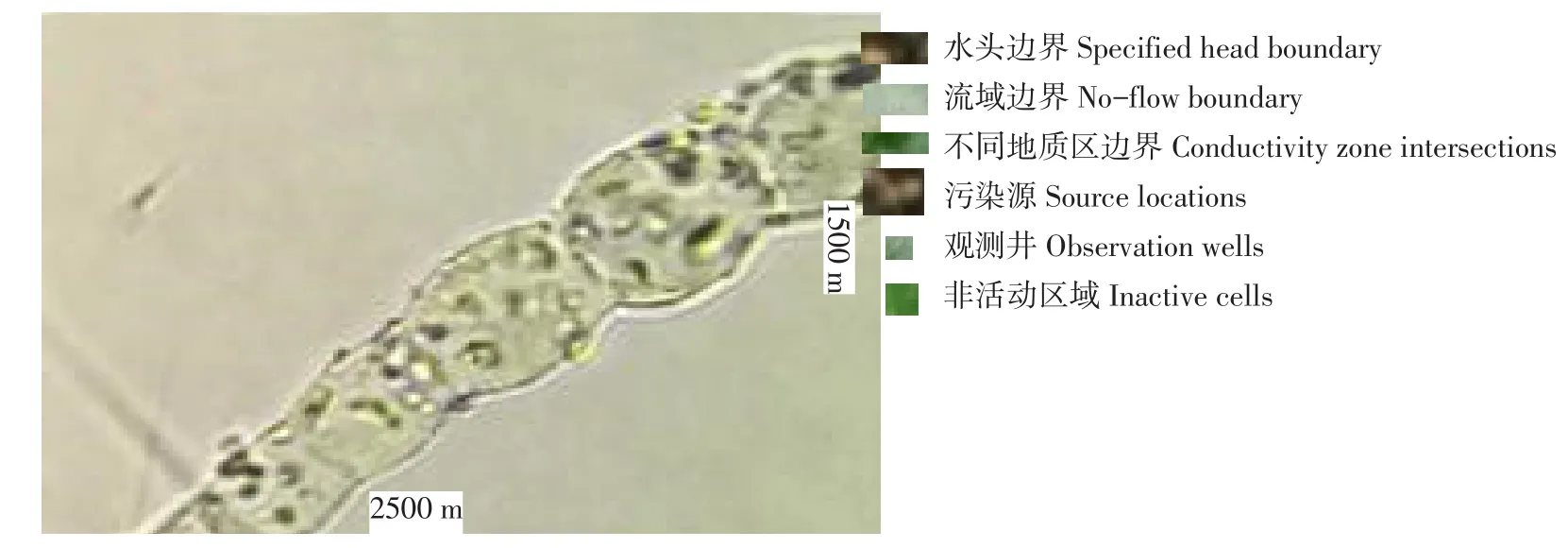
图5 案例3含水层结构平面Fig.5 Aquifer structureplaneof case 3
图6 不同替代模型对案例3污染源释放历史反演结果Fig.6 Retrieval results of different surrogate models on the release history of case 3 pollution sources

表7 案例3反演结果误差Table7 Retrieval result error in case 3
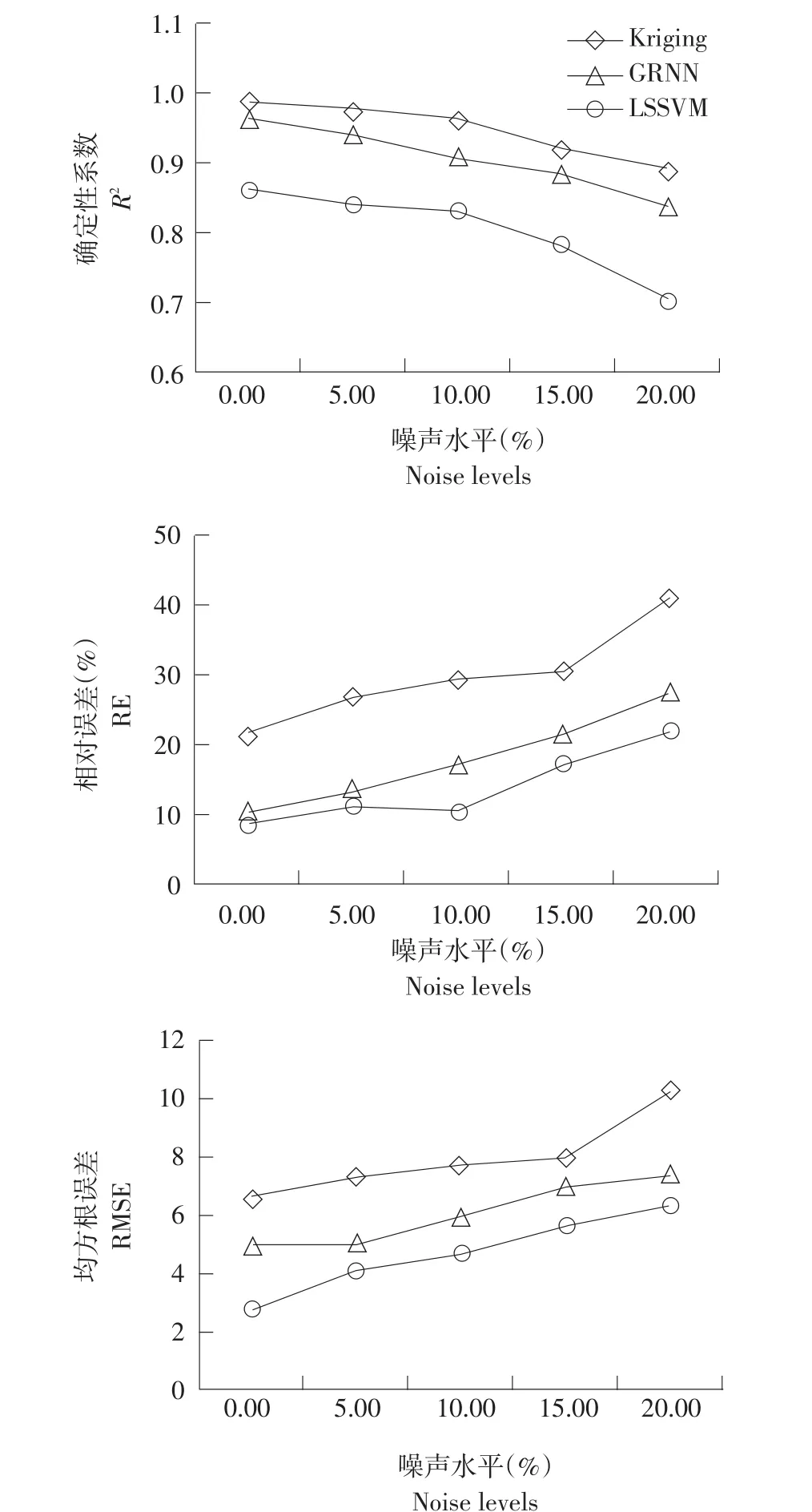
图7 在不同噪声水平下替代模型反演结果误差分析Fig.7 Error analysis of the retrieval results of surrogate models at different noiselevels
随噪声水平增加,反演结果误差增加。在无噪声情况下,运用GRNN替代模型反演精度较低,反演结果较合理。当观测值存在噪声情况下,即使在低噪声水平下,反演结果RE高达26.88。在高水平噪声条件下,R2降至0.7,反演结果较差。而LSSVM替代模型,随噪声水平增加,反演结果误差变大,但该模型表现稳定,误差值上升平稳。在中等噪声水平或以下,反演结果和Kriging替代模型反演结果接近。与前两种替代模型相比,Kriging替代模型在噪声水平a=10%情况下,R2在0.96以上,RE为10%,RMSE小于5,说明在中等噪声水平下,运用Kriging替代模型反演精度良好。此外,由图7可知,即使在高水平噪声下,Kriging替代模反演精度被接受。
综合以上3个案例反演结果发现,Kriging替代模型适用于所有案例,观测值存在较高水平噪声时可获得精度较高反演结果。LSSVM替代模型适用于所有案例,但在观测值噪声水平较高情况下适用性次于Kriging替代模型。而GRNN替代模型仅在案例1和案例2水文地质条件下适用性优良,在案例3中反演精度较低。尤其在观测值存在噪声情况下,反演结果可能不被接受。提出替代模型主要目的是提高计算效率。在3个替代模型反演过程中,分别记录反演所需时间。对比可知,运用Kriging替代模型反演过程所需计算时间是LSSVM和GRNN反演所需时间2倍。
4 结论
本文分别运用Kriging、LSSVM和GRNN建立替代模型,结合遗传算法反演3种不同含水层条件和多个噪声水平下地下水污染源释放过程。重点讨论相同情况下3种替代模型反演精度和各单一替代模型在不同复杂情况适用性,研究成果可为解决案例相似条件下地下水污染源释放历史反演现实问题中替代模型有效选择提供试验支撑。本文在研究过程中设定3种案例中监测污染物稳定不可降解,但监测污染物可被降解和吸附,后续将研究不稳定污染物污染源反演。
a.GRNN替代模型仅在简单水文地质情况下适用性较好,其他较复杂情况下反演结果较差,尤其在非稳定流地下水含水层,但反演时间短。
b.LSSVM替代模型虽在复杂水文地质情况适用性优良且反演时间短,但当观测值存在较大观测误差时,反演精度下降,适用性较差。
c.在3种替代模型中Kriging替代模型最为稳定,在复杂水文地质情况适用性更强,更适用于观测值存在噪声情况。但Kriging替代模型反演所需时间成本较高,现实应用应根据实际情况选择替代模型。

