基于火焰体积法的燃烧室熄火特性数值模拟预测

黄 夏，王慧汝

(中国航空发动机研究院基础与应用研究中心，北京101304)

1 引言

随着航空发动机对推力的要求越来越高，燃烧室必将向高温升燃烧方向发展[1]。要实现高温升，则需减少用于掺混、冷却的空气量，使进入主燃区参与燃烧的空气量增多，而导致燃烧室的熄火边界变窄，火焰稳定困难[2]。另一方面，民用飞机污染排放要求日益严格，为降低航空发动机的污染物(NOx、CO等)排放，目前已应用或正在研制的低污染燃烧室，如贫油预混预蒸发燃烧室(LPP)[3]、贫油直喷燃烧室(LDI)[4-5]、富油-淬熄-贫油燃烧室(RQL)[6-9]、催化燃烧室、驻涡燃烧室(TVC)[10]和双环预混旋流燃烧室(TAPS)[11-13]等，其设计工作点大多远离化学恰当比并偏向燃料的可燃极限，使得燃烧室更有可能发生熄火[14]。这些要求都使得准确预测火焰的吹熄特性成为一项十分重要的工作。

火焰稳定的机理是来流速度与火焰传播速度之间的平衡[15]。从理论上讲，对于一个特定的燃烧现象，只要比较流场中每一点的流动速度与火焰传播速度，就能预测火焰的吹熄特性。这种方法应用于层流火焰还较为可行，因为层流火焰的流场可近似看作线性分布，如作者对本生灯火焰吹熄特性的研究[16-19]。然而由于工程实际中的燃烧现象大部分处于湍流流态，使用上述方法预测熄火特性很难实现。因此，在预测实际燃烧现象的熄火特性时，往往采用以能量守恒为基础的方法。

对于基于能量守恒预测熄火特性的方法，早期研究者主要针对钝体火焰进行了研究，并提出了两大模型：一是以Longwell等[20]为代表的回流区均匀搅拌器模型，二是以Zukowski等[21]为代表的回流区点火模型。以Longwell对钝体的研究为基础，Ballal等[22-23]针对钝体燃烧室均相燃烧的贫熄特性进行了研究，考察了14种钝体燃烧室的熄火特性，研究中燃烧室来流工况范围为压力0.02～0.09 MPa(表压)，温度300～575 K；之后又针对钝体火焰的非均相燃烧进行了研究。在这些研究的基础上，Lefebvre[24]针对8种型号发动机的燃烧室进行了贫油熄火试验，最终得到液态燃料贫油熄火特性关系式。

目前，在航空发动机燃烧室设计中采用的熄火特性预测模型，基本上采用的是Lefebvre关系式或其衍生形式，但该半经验关系式对于航空发动机燃烧室熄火边界预测的通用性还有待考证。Mongia等[25]用实验的方法验证了目前的贫油熄火经验或半经验关系式，结果表明没有一个关系式能应用于现代涡轮发动机燃烧室贫油熄火的预测计算。因此，目前采用Lefebvre关系式或其衍生形式进行预测，大多只能得到熄火特性的定性变化趋势以用作设计时参考，而无法得到与实验数据符合程度较高的结果。

Lefebvre的贫熄关系式中，参与燃烧的空气量是整个来流的空气量，燃烧区大小是掺混孔之前整个燃烧室的体积。而谢法等[26]所做的燃烧室贫熄可视化实验研究表明，当燃烧室接近熄火时火焰只存在于火焰筒头部的一部分空间。Mongia[27]在报告中首次提出，用燃烧区大小代替Lefebvre关系式中燃烧室体积大小，但没有深入研究这种直接替代是否合理。

谢法[26]以某旋流燃烧室为基础，通过改变旋流器、主燃孔结构研究了不同结构下火焰的贫熄特性，发现不同燃烧室结构其熄火时的火焰体积大小不同。火焰体积大小不同意味着参与燃烧的空气量也不相同，因此只要确定了熄火时的火焰体积大小和参与燃烧的空气量，就完成了对Lefebvre贫熄关系式的改进，这种改进的方法称为火焰体积法。采用火焰体积法模型计算文献[26]所用燃烧室的贫熄特性，与试验结果误差在±15%左右；而Lefebvre预测公式的误差在±45%左右。

文献[26]中的火焰体积法仅用于描述熄火特性实验数据的变化规律，并不具备预测熄火特性的功能，但该研究说明了用火焰体积代替Lefebvre模型中燃烧室体积的可行性。为此，本文在文献[26]中火焰体积法的基础上，通过数值模拟提取燃烧室中的火焰体积，将该方法改进成了可预测燃烧室熄火特性的方法。

2 火焰体积迭代数值预测方法

Lefebvre的贫熄关系式为：

式中：qLBO为贫油熄火时油气比，A′为经验系数，fPZ为主燃区空气比例，Vc为掺混区前的火焰筒体积(即主燃区体积)，ṁa为来流空气质量流量，p3为来流空气压力，T3为来流空气温度，Dr为液滴平均直径，λr为液体燃料蒸发系数，LHVr为燃料低位热值，D0为液滴在不同温度下的初始直径。Lefebvre建议A′fPZ取29。

谢法的火焰体积法模型为：

式中：α为燃烧室头部进气量，也即头部参与燃烧的空气量，其值由头部进气面积与燃烧室总进气面积的比值确定；β为燃烧室接近熄火时的火焰体积与主燃区体积之比；K为经验系数，取43。

根据式(2)，只要确定α、β，就能预测出贫熄油气比。按照流动相似，α只与燃烧室结构有关，通过数值模拟很容易确定。若也想采用数值模拟方法得到β，则首先需知道燃烧室的油气比——这一油气比正是需要通过式(2)计算得出。因此，式(2)并不能直接用于预测贫熄油气比，需要采用迭代的方法才能实现。该方法的步骤如下：

(1) 假设燃烧室油气比为qn-1，当n=1时即为燃烧室油气比的迭代初始值q0(理论上可为任意值，为加快收敛速度，建议取0.005 0)。以q0为燃烧室油气比，通过数值模拟方法得到燃烧室热态流场。

(2) 根据数值模拟结果，确定αn-1与βn-1，n=1时即为α0与β0。

(3) 将各数据代入式(2)，得到预测的贫熄油气比qLBO,n-1，n=1时即为qLBO,0。

(4)若相对误差ε的绝对值 ||

ε=，则取为燃烧室油气比重新数值模拟得到新的热态流场。若qLBO,n-1-qn-1＞0，Δq取正值；反之 Δq取负值。为加快收敛，| |Δq建议取值范围0.000 1～0.001 0。

(5) 根据新的数值模拟结果得到qLBO,n。由于燃烧室设计中，贫熄油气比的预测误差在±10%以内都可接受，因此反复进行(1)～(4)步，直到||ε≤0.1，此时的qLBO,n即为贫熄油气比的预测结果。

2.1 火焰体积的确定

文献[26]中，火焰体积通过观测火焰的发光区域计算得到。对于数值模拟结果，需采用别的标准来确定火焰的边界。根据王慧汝的研究[28]，本文选取当地当量比在航空煤油可燃边界范围内的区域作为火焰区域。常温常压下，碳氢燃料可燃边界的当量比ϕ范围为0.5～2.0。可燃边界与压力、温度都有关系。当压力高于标准大气压时，压力增大，可燃边界扩大，但主要是富燃边界扩大，贫燃边界基本无变化。温度增高，可燃边界也扩大，但幅度很小[29]。本文研究的是贫油熄火特性，因此在任意来流工况下，都将可燃边界范围近似看作不变，即当量比0.5～2.0。

2.2 温度、压力与空气流量

式(2)中K基于一系列来流空气压力271.5 kPa、温度288 K的熄火实验结果所得[26]，当来流空气的压力、温度与上述实验条件不同时，如果直接将这些数据代入式(2)，其预测结果是否准确有待商榷。

为了能直接使用式(2)，式中的压力、温度应分别取271.5 kPa和288 K，空气流量则依据流动相似原理变换为上述压力与温度下所对应的流量。根据火焰稳定与吹熄的基本原理，影响火焰是否吹熄的两大因素为来流速度与燃料浓度，而来流速度由空气流量决定。因此，为保证熄火特性相似，相似变换前后应保证进口马赫数相同：

式中：无上标表示实际工况数据，有上标表示相似变换后数据，下同。

根据空气动力学原理，燃烧室进口空气流量为：

式中：C为只与工质有关的常数，A为燃烧室进口面积。当Ma相同时，q()λ也相同，则有：

取p*′=271.5 kPa，T*′=288 K，根据式(5)可得经相似变换后的空气流量。

3 数值模拟设置

3.1 燃烧室结构

本研究中的燃烧室结构如图1所示，这一结构截取了该燃烧室的单头部扇形段。燃烧室头部具有两级旋流器，其中Ⅰ级为斜切孔旋流器，Ⅱ级则为径向旋流器。火焰筒内外环各有两个主燃孔。其中一孔对应喷嘴中心线，直径较小；另外在侧边(如果从全环角度考虑，就是两个相邻喷嘴之间)各有两个半孔，直径较大。根据计算，其主燃区体积(据文献[1]，即为掺混区前的火焰筒体积)Vc=0.001 12 m3。本研究采用多面体网格，网格总数493万。

3.2 计算模型

采用商业软件进行数值计算。胡斌[30-31]的研究中已经就各种湍流、燃烧模型对燃烧室流场计算的影响进行了研究，根据该研究本文数值计算中各模型、方法的设置如表1所示。本文暂不考察雾化对贫熄特性的影响，因此燃料选用气态航空煤油(计算中组分为C12H23)。燃烧机理采用Kundu[32]的16组分、23步反应的C12H23简化反应机理。

表1 计算设置Table 1 Calculation settings

4 预测过程

4.1 基准工况

为验证上述预测方法，首先以一组边界条件为基准工况(表2)，同时取q0=0.005 0。

表2 基准工况边界条件Table 2 Boundary conditions of basic operation condition

根据数值计算结果，两级旋流器进口空气流量为0.056 56 kg/s，则α0=0.135 9。

由于本文数值计算的燃烧模型是非预混燃烧模型，这一模型直接计算的是守恒标量混合分数Z，而当地的当量比与Z相关。一般定义燃油流中Z=1，空气流中Z=0，因此当量比和混合分数的转换关系为：

式中：FARst为化学恰当的油气比。对于C12H23，FARst=0.068 53。

图2为中心纵截面的当量比分布。将图中当量比0.5～2.0的区域分离出来，即可得到图3中绿色部分。利用数值计算软件中的体积积分功能，可得到绿色区域体积即火焰体积Vf0=1.291×10-5m3，则β0=0.011 6。

将α0、β0代入式(2)可得qLBO,0=0.006 76，ε=0.352。由于且ε＞0，则取q1=0.006 0重复上述数值计算过程，可得qLBO,1=0.003 95，ε=-0.342。下一步取q2=0.005 5继续重复数值计算过程。迭代步骤见表3，可见当计算到q4=0.005 2时，qLBO,4=0.004 97，ε=-0.044，符合的要求，结束迭代过程。最终贫油熄火预测油气比为0.004 97。根据实验结果，该燃烧室的慢车贫油贫熄油气比在0.004～0.006之间，预测相对误差小于±24%。若采用Lefebvre模型，预测贫熄油气比为0.000 334，误差在-90%以上。

表3 熄火预测迭代过程Table 3 Iteration of the flameout prediction

本次预测共迭代了5次。在采用计算机10线程并行计算的情况下，单次迭代的计算时间约为2 h。

4.2 收敛性分析

为证明上述算法的收敛性，选取数组燃烧室油气比以观察预测结果的变化趋势，计算结果如表4所示。可见，当qn-1远离0.005 2时，ε的绝对值逐渐增大。从根据表4结果得到的图4可看到，在所取的初始油气比范围内(0.002 5～0.007 0)，qLBO,n-1随qn-1的增加单调递减。图中qLBO,n-1=qn-1的直线与qLBO,n-1=f(qn-1)的曲线有且只有一个交点，说明在这一油气比范围内，采用上述算法最终必然收敛向一个唯一的贫熄油气比结果。

表4 不同燃烧室油气比的预测结果Table 4 Prediction results of different fuel-air ratio

5 燃烧室流通面积对贫熄的影响

当燃烧室火焰筒各进气装置流通面积发生变化时，如扩大旋流器流通面积或缩小主燃孔流通面积，必然会对贫油贫熄油气比产生影响。不过采用Lefebvre的式(1)，旋流器流通面积的变化在贫熄油气比预测值上体现不出来，预测结果均为0.002 48。如果采用改进的火焰体积法，燃烧室结构变化的影响在α、β上均可以体现出来，从而影响最终的贫油贫熄油气比预测结果。

5.1 旋流器

主燃区参与燃烧的空气，有很大一部分由旋流器提供。理论上讲，如果旋流器流通面积扩大，则参与燃烧的空气量增多，主燃区当量比下降，熄火性能变差，即贫熄油气比会提高；相反，如果旋流器流通面积缩小，则贫熄油气比会下降。

5.1.1 Ⅰ级旋流器

以第3章的燃烧室结构作为基准结构，分别扩大、缩小Ⅰ级旋流器的流通面积；采用第4章基于数值模拟的火焰体积法，得到贫熄油气比的预测结果如表5所示。可见，随着流通面积的增大，α、β均会增大。分析式(2)中qLBO随α与β的单调性可知，qLBO随α单调递增，随β单调递减。扩大旋流器流通面积虽有利于加强雾化与掺混，但空气量增多导致带走的热量增多，而这对熄火特性的影响高于前者，因此最终qLBO随流通面积的扩大而提高。从数值上看，Ⅰ级旋流器流通面积每变化20%，贫熄油气比变化约3%～5%。

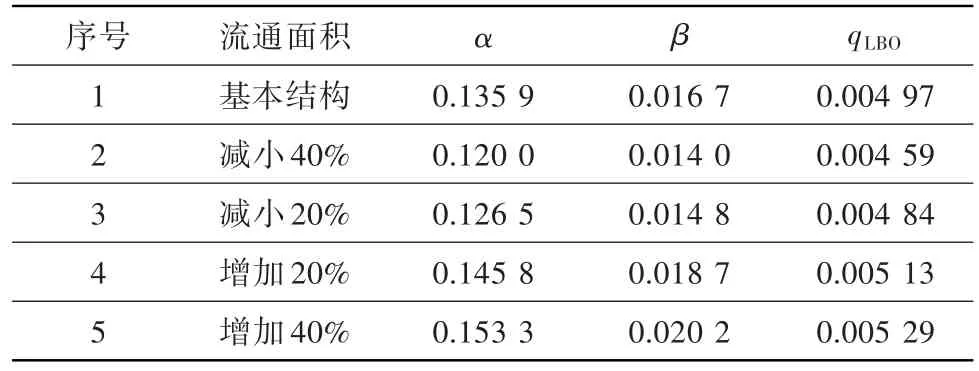
表5 Ⅰ级旋流器流通面积与贫熄特性的关系Table 5 Flameout characteristics with different flow areas of the primary swirler

5.1.2 Ⅱ级旋流器

分别扩大、缩小基准结构燃烧室Ⅱ级旋流器的流通面积，得到贫熄油气比的预测结果如表6所示。可见贫熄油气比随Ⅱ级旋流器流通面积扩大而提高，与理论分析的变化趋势一致。从数值上看，Ⅱ级旋流器流通面积每变化10%，贫熄油气比变化约4%～12%。

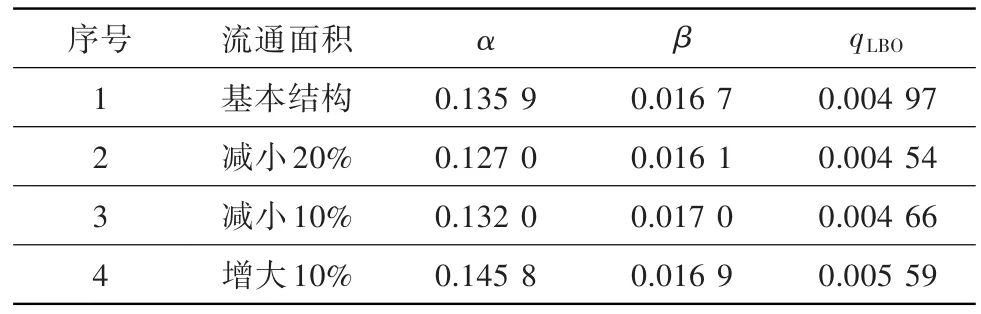
表6 Ⅱ级旋流器流通面积与贫熄特性的关系Table 6 Flameout characteristics with different flow areas of the secondary swirler

5.2 主燃孔

主燃孔进气对主燃区燃烧也有很大影响。仍以基准结构为基础，分别扩大、缩小主燃孔的流通面积，预测结果如表7所示。可见，贫熄油气比随主燃孔流通面积的扩大而减小。如果增大主燃孔流通面积，主燃孔气流量增大，整个火焰筒的流量分配将发生变化，旋流器空气流量减小。根据前文分析，贫熄油气比减小。可见，旋流器空气流量分配对贫熄特性起到了主要作用。从数值上看，主燃孔流通面积每变化15%，qLBO变化约3%～5%。

表7 主燃孔流通面积与贫熄油气比的关系Table 7 Lean flameout characteristics with different flow areas of primary holes

6 结论

(1)经过改进的火焰体积法能预测燃烧室的贫油熄火特性，可以体现出火焰筒结构对贫熄特性的影响，在基准工况下预测误差低于±24%。

(2)旋流器空气流量对燃烧室贫熄特性具有十分重要的影响。不论是改变旋流器流通面积，还是改变主燃孔流通面积，只要导致旋流器空气流量比例增大，贫熄油气比就会增大；反之贫熄油气比减小。

(3)未来研究中，将通过实验来定量验证这种方法预测不同燃烧室结构贫熄特性的精度，同时也借助实验研究结果来得到更准确的火焰体积提取方法。另外，也将考虑采用液态燃料研究燃料雾化特性对贫油熄火特性的影响。