新疆乌鲁木齐市百日咳动力学模型研究与应用
苏瑞童 闫茂胜 王蕾
【摘 要】基于新疆乌鲁木齐市2004-2015年新发的百日咳数据,根据百日咳的传播机制,我们建立相应的动力学模型,并根据模型预测疾病的波动趋势。拟合效果较为理想,并计算出乌鲁木齐百日咳传播的基本再生数R0≈1.1030;预测结果表明乌鲁木齐百日咳不会消亡仍会继续流行,相关部门应加强对疾病的防治控制。
【关键词】百日咳;动力学模型;拟合;预测;基本再生数
中图分类号: TV131文献标识码: A 文章编号: 2095-2457(2019)36-0262-002
DOI:10.19694/j.cnki.issn2095-2457.2019.36.124
0 引言
百日咳(Pertussis或Whooping Cough)是由百日咳鲍特菌引起的一种可预防的严重急性呼吸道传染病[1],传染性较强,它通过呼吸道吸入含有百日咳鲍特菌的空气飞沫被感染。在使用百日咳疫苗以前,百日咳是婴幼儿死亡的主要原因之一,是全世界最常见10大感染致死性疾病之一。20世纪初,在婴儿中病死率高达10%。1974年全球实施扩大免疫计划以来,世界范围内的百日咳得到有效控制,发病率和病死率大幅下降,但近年来,百日咳在世界范围内大规模重现,主要涉及婴儿和青少年[2-3],百日咳的发病率呈现出缓慢、稳定的增多趋势[4]。
由于新疆地区是一个多民族聚居地区,地广人稀,经济发展较为落后,公共卫生资源相对缺乏,百日咳疫苗接种率相对较低,导致百日咳发病率依然处于较高水平。一组由新疆维吾尔自治区疾控中心报告数据显示,2004-2012年新疆百日咳报告发病数3760例,死亡5例,年平均报告发病率为2.02/10万居全国百日咳发病率首位;病例主要集中在0-15岁儿童,占总发病数的99.36%。新疆乌鲁木齐地区虽较为发达,但人群分布、环境因素等的影响刺激了百日咳的流行,使得百日咳的患病率逐年上升。在乌鲁木齐地区,患病人群多偏向于儿童和青少年。如何预防和控制新疆乌鲁木齐地区百日咳的流行逐渐被提上了日程。
百日咳问题不仅是一个公共卫生问题,更是一个社会问题、政治问题和经济问题,严重影响着我国人民的健康和家庭幸福,更重要的是影响到社会稳定和经济的可持续发展,是我国现阶段最为突出的公共卫生问题之一。百日咳不仅严重威胁人类健康并且是导致年长儿及成人长期咳嗽的常见病因,对新疆社会、经济文化科技的协调发展产生极其负面的影响。因而,如何控制百日咳在乌鲁木齐的传播与流行是急需迫切需要解决的重要医学和社会问题。
随着百日咳在世界范围内的传播和流行,如何预防、控制百日咳的流行已成为世界各国关注的重点内容之一。近十年以来,国内外许多学者都对百日咳的传播机制和流行进行了研究与分析。文[5]研究了新疆喀什地区百日咳流行趋势,利用时间序列分析方法建立了ARIMA乘积季节模型,结果较好地拟合及预测了新疆喀什地区百日咳的流行趋势,为新疆喀什地區百日咳疫情的暴发流行的控制提供理论依据。在传染病研究中,方法还有许多,例如文[6]研究了蓬溪县1953-1992年百日咳发病季节特征,建立了余弦模型,求得了发病高峰时点及高峰时区,对疾病的预防和控制有巨大意义。
目前,对传染病的研究方法中最基本的方法是描述性研究,文[7]研究了2004-2012年新疆百日咳疫情资料,发现疾病与人群的构成有较大的关系。在国外,也有较多的学者对百日咳的流行趋势和影响因素进行了一定程度的研究,但大多数都是描述性的研究,没有更进一步的提出更好的控制策略。文[8]研究了美国百日咳与哮喘高患病率之间的联系,结果发现应将哮喘患者定义为百日咳疫苗的目标群体,这对如何切断百日咳的流行提供了目标基础。百日咳在婴儿和青少年中的流行较为严重,但疫苗的产生,能有效降低百日咳的感染率。文[9]研究了拉丁美洲不同国家百日咳的疾病数据。结果发现在这个地理区域中,这些病例中的大多数都与6个月以下的接受不到三剂疫苗的患者对应。在大量的研究中,我们还发现注射抗生素也能够有效地预防百日咳。文[10]研究了国百日咳患病人群的临床特征,通过对患病人群数据的研究,发现抗生素可以降低百日咳的传播率,并且提出了一剂Tdap助推器的新建议。
在百日咳的发生、发展中,咳嗽是主要的症状,如何提高诊断百日咳的灵敏度,这是一大难题。文[11]研究了83例经实验室确诊的百日咳患者和1132例未经实验室证实的百日咳,通过进行血清学、聚合酶链反应来诊断。结果在百日咳患者中,阵发性咳嗽的敏感性为90%,特异性为25%。新疆地处祖国边缘,整体医疗水平较为落后。如何更好地对百日咳进行干预和控制,表现得更为迫切。
基于以上研究,本文建立切合乌鲁木齐市百日咳的传播规律的动力学模型,根据收集到百日咳病的发病数据,以及其他相关的其他数据(人口数据等),采用最小二乘估计等概率统计知识对各种参数进行估计。最后利用数学软件(Matlab)进行数值模拟,验证分析结果拟合数据并预测百日咳病的流行趋势。
1 主要结果
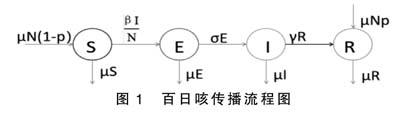
根据百日咳的传播机理,将总人口划分为四个仓室:易感者(S),潜伏者(E),感染者(I),以及恢复者(R)。我们给出如下百日咳的传播流程图(如图1所示)。
图1 百日咳传播流程图
进而建立如下百日咳的传播动力学模型
■=μN(1-p)-■+μS,■=■S-(σ+μ)E,■=σE-(r+μ)I,■=rI+μNP-μR,N(t)=s(t)+E(t)+I(t)+R(t)
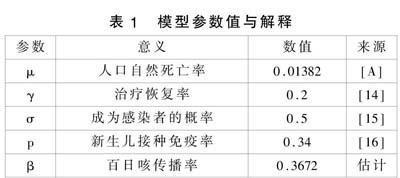
其中,S(t)代表t时刻易感者的数量;E(t)代表时刻潜伏者的数量;I(t)代表t时刻感染者的数量;R(t)代表t时刻恢复者的数量;N(t)代表t时刻总人口数。参数的含义解释如表2所示。
首先,我们把模型(1)中的前四个方程相加,可得到
■≡0
则解出
N(t)≡N0(其中N0为单数)
显然,模型(1)有一个唯一的平衡点P0((1-p)N0,0,0,pN0)
根据文献[12-13]中计算下一代再生矩阵及基本再生数的方法,我们定义
f=■ 0 υ= (μ+σ)E(r+μ)I-σE
注意到模型(1)中的平衡点为P0,
则可得:
F=■且V=■
则下一代再生矩阵是
FV-1=■
由此可得模型(1)的基本再生数为R0=ρ(FV-1),其中ρ(FV-1)表示矩阵FV-1的谱半径,经计算可得:
R0=■
定义W(t)为百日咳累计发病数,则由模型(1)可得■=■,
根据图2所示,可知W(0)=I(0)=10.其模型(1)的其他初值分别假设为:S(0)=1000000,E(0)=63950,R(0)=1000。
表1 模型参数值与解释
利用最小二乘法,采用模型(1)去拟合百日咳的累计发病数(见图2)。在此基础上估计出β≈0.3672,模型的其他参数见表2。经计算,可得基本再生数R0=1.1030>1,这表明乌鲁木齐百日咳仍会继续流行。
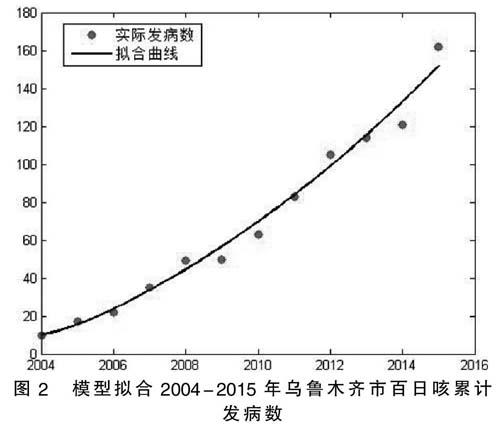
图2 模型拟合2004-2015年乌鲁木齐市百日咳累计发病数
如图2所示,横坐标是时间,纵坐标是对应时间百日咳发病累积例数。红色为实际值,黑色曲线为拟合曲线。由此图可看出,模型(1)的解基本能拟合出2004-2015年乌鲁木齐市百日咳的实际累计发病数据。2004-2015年每年新发百日咳数量总体变化较为平稳,2015年,乌鲁木齐市百日咳累积发病例数达到160余人。
图3 2004-2035年乌鲁木齐市百日咳的累计发病数预测图
基于表2的参数值,可利用模型(1)预测乌鲁木齐市百日咳的流行趋势。如图3所示,蓝点表示从2004-2015年对应百日咳实际累计新发病数据,红色曲线为使用模型(1)的拟合曲线,绿色部分是拟合曲线的95%置信区间。从图3可以看出,保守预测至2035年,乌鲁木齐市百日咳累计新发病数会持续上涨,相关部门应做好百日咳的防治防控措施,提高百白破疫苗的覆盖率。
【参考文献】
[1]徐勇胜,百日咳临床特征研究进展[J].中国实用儿科杂志,2016,31(9):712-715.
[2]徐红梅,郑佳佳.百日咳临床特点及流行病学研究进展[J].中华实用儿科临床杂志,2014,29(22):1681-1682.
[3]Cherry JD,Paddock CD. Pathogenesis and histopathology of pertussis:implications for immunization[J]. Expert Rev Vaccines, 2014,13(9):1115-1123.
[4]張柳,赵建宏,张庶民.百日咳流行病学研究进展[J].中国疫苗和免疫,2008,14(6):559-564.
[5]陈佳,谢娜,吴秀峰,等. 基于ARIMA乘积季节模型的新疆喀什百日咳流行趋势分析[J].新疆医科大学学报,2017,40(3):380-384.
[6]王成科,廖清廉,吕勇.利用数学模型探讨百日咳发病季节特征[J].数理医药学杂志,2000,13(1):67-69.
[7]陈涛,谢娜,甫尔哈提等.2004-2012年新疆维吾尔自治区百日咳流行特征分析[J].疾病监测,2013,28(11):911-913.
[8]Kline JM,Lewis WD,Smith EA,et al. ertussis:a reemerging infection[J].Am Fam Physician,2013,88(8):507-514.
[9]L.H.Falleiros Arlant, De Colsa, Agustin, D. Flores, et al. Pertussis in Latin America: epidemiology and control strategies[J].Expert Review of Anti-infective Therapy,2014,12(10):1265-1275.
[10]J.M.Kline,W.D. Lewis,E.A. Smith,et al.Pertussis:a reemerging infection[J].Am Fam Physician,2013,88(8):507-514.
[11]N. Miyashita,H. Akaike, H. Teranishi,et al. Diagnostic value of symptoms and laboratory data for pertussis in adolescent and adult patients[J]. BMC Infect Dis,2013,13(2):129.
[12]O. Diekmann, J. A. P. Heesterbeek, J. A. J. Metz ,On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations[J]. Journal of Mathematical Biology,1990,28(4):365-382.
[13]P. van den Driessche, J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J].Mathematical Biosciences,2002,180(1-2):29-48.
[14]张喜凤,小儿百日咳综合征的临床特点及治疗分析[J].中国继续医学教育,2018,10(09):91-93.
[15]王丽婵,马霄,孟丽,徐颖华,骆鹏,卫辰,张庶民,侯启明.百日咳疫苗免疫接种策略及相关研究进展[J].中华预防医学杂志,2013,47(1):70-73.
[16]郝晓燕,薜琴,梁春莉.婴儿百日咳综合征临床分析[J].世界最新医学信息文摘,2016,16(92):202-205.

