基于CoES模型的商业银行系统风险评价研究
李嘉晨

摘 要:本文通过CoES模型,测度了16家中国上市银行系统风险贡献度大小,并通过面板回归对影响系统风险贡献度的因素进行分析。研究表明:国有大型商业银行的系统重要性普遍高于股份制商业银行和城市商业银行,中国工商银行的系统重要性在所有商业银行中最高,中信银行系统重要性位列股份制银行之首,城商行中则是北京银行的系统重要性最强;广义货币增长率、对外投资依存度、期限利差、市值规模、權益乘数、资本充足率、总资产收益率、不良贷款率均会显著影响系统风险贡献度大小。
关键词:系统风险;系统重要性银行;CoES模型
DOI:10.3969/j.issn.1003-9031.2019.12.002
中图分类号:F832.33 文献标识码:A 文章编号:1003-9031(2019)12-0014-13
自2008年次贷危机爆发以来,人们深刻认识到了金融机构间的风险传染可能带来系统风险,学界与实务界也围绕系统风险开展了大量研究,一个重要研究方向就是有关系统风险测算及关于系统重要性机构的鉴定。随着2014年银监会印发《商业银行全球系统重要性评估指标披露指引》及2018年三部委联合发布《关于完善系统重要性金融机构监管的指导意见》,我国有关系统重要性机构的监管体系不断完善,相关评价体系仍在进一步探索。
一、文献综述
学界关于系统风险度量的研究,大体上可以按照数据来源的不同,将之分为基于宏观变量和资产负债表的指标法和基于市场数据的衡量法。一般而言,传统的指标法大多采用资产负债表信息,结合宏观变量构建指标体系对系统风险衡量。近年来主流风险度量模型更多的是从资产价格角度出发,利用市场数据对系统风险进行度量,其中就包含以在险价值(VaR)为基础的系统风险度量模型和以预期损失(ES)为基础的系统风险度量模型。
在基于VaR为基础的风险度量模型中,最具代表性的就是条件在险价值(CoVaR)指标,其定义为当机构i处于极端风险时,整体金融系统的在险价值大小。Adrian&Brunnermeier(2009)认为附加条件下系统的在险价值与无条件下系统在险价值大小之差ΔCoVaR是机构i对整体系统风险的影响。围绕ΔCoVaR指标,国内外学者对其估计方法和定义展开进一步研究。在估计方法上,Adrian等(2011)主要利用分位数回归方法计算了CoVaR的大小;谢福座(2010)最早开始将Copula函数与CoVaR结合,对亚洲三大股票市场指数的风险溢出效应进行实证检验;高国华和潘英丽(2011)提出用AR-GARCH模型,结合正态分布及t分布下的分位数进而得到动态CoVaR的大小。在定义延申方面,Chan-Lau等(2009)提出一个类似CoVaR的指标Co-Risk,通过计算极端分位数情况下的机构的条件CDS价值,度量机构间信用风险关联性;国内学者白雪梅、石大龙(2014)从实际监管需求的层面出发,通过面板数据回归且用滞后一期的解释变量进行预测,最终得到Forward-ΔCoVaR指标,与ΔCoVaR对比发现二者呈负相关关系,此时基于该指标进行宏观审慎监管则是逆周期的。
在基于ES为基础的风险度量模型中,学者从定义上做了较多拓展。Acharya等(2009,2010)在预期损失ES指标的基础上,提出了系统风险预期损失(SES)和边际预期损失(MES)两个指标,用于表示某一银行的预期资本短缺及个体金融机构对系统风险边际贡献度。Engle也先后与Brownlees(2011)和Acharya(2012)合作,提出了系统风险指数SRISK,该指标测度了市场未来一段时间内收益率低于某一水平时,某一金融机构的预期资本短缺。Banulescu&Dumitrescu(2015)提出了成分预期损失(CES)指标,在满足欧拉可加性定义下,考虑单一银行在整个银行系统中的规模权重因素,将银行系统的预期损失ES根据单一银行权重,分解为不同成分预期损失。
由于CoVaR指标无法覆盖超过分位数点的尾部风险,而ES指标无法测度机构对于系统的溢出效应,Adrian&Brunnermeier(2016)提出条件预期损失(CoES)指标的构想。国内学者李政等(2019)参照前者的构想,构建了自己的CoES指标。因该指标可以视为是CoVaR与ES交叉融合下的产物,既涵盖了超过VaR门限的尾部损失,又度量了机构风险的溢出程度,下文将基于CoES指标对商业银行系统风险贡献度进行度量,并以此给出银行系统重要性排名,并对影响系统风险的因素进行实证分析。
二、基于ARMA-EGARCH的CoES模型
学界关于系统风险的定义虽存在分歧,但都强调系统风险是一种由于个体风险导致行业整体风险的情形,系统风险具有传染性及负外部性两大特点。此外,由于投资者普遍存在一定的正反馈行为,这会致使单一银行发生财务困境时,银行市场上出现挤兑或资产抛售,致使整个系统遭受损失。同时,银行往往出于安全性考虑,在经济增长时期不会有太过激进的行为,其正向收益相对平稳,而负向损失相对聚集,系统风险还存在厚尾性和非对称性两大特点。基于几大特征的考虑,我们选择在GED分布下的ARMA-EGARCH模型,结合CoES指标对系统风险进行测算。
(一)CoES和下行ΔCoES的定义
根据Adrian and Brunnermeier(2016)提出的构想,CoES指标可以定义在银行i的收益率小于显著性水平p所对应的分位数的条件下,银行系统的收益率的期望大小。
同时,为了构造下行风险溢出和左尾部依赖性的测度指标,李政等(2019)在参考ΔCoVaR的定义后,给出了下行ΔCoES的定义:
为了方便不同机构间系统风险贡献度的比较,进而对系统重要性排名,参照前人对%ΔCoVaR指标的设计,本文对ΔCoESL指标进行标准化处理:
其中,关于显著性水平的选取,考虑到现实中我国商业银行一般选择99%作为其置信水平,故而α此处取值为1%。同时,对于风险价值VaR所设置的持有期也参考商业银行标准设置为1天,而计算CoES指标时则考虑了未来一个月的收益率,兼顾了实时性的要求。
(二)基于GED分布下ARMA-EGARCH模型的CoES估计方法
本文主要采用ARMA-EGARCH模型来估计CoES指标,同时假设银行个体的收益率和银行系统收益率估计中对应的残差序列服从于广义误差分布(GED),主要原因如下:一是利用ARMA-EGARCH模型进行估计,不仅有利于解决金融时间序列数据的自相关和异方差问题,还有利于拟合时间序列对利好及利空消息的非对称反应(杠杆效应);二是GED分布的假设相对正态分布假设更能拟合时间序列数据普遍存在的尖峰厚尾特征;三是CoES指标及下行ΔCoES指标设计为对系统风险贡献度的度量,即主要度量了一种溢出效应。综上所述,该模型可以对系统风险存在的传染性、负外部性、非对称性、厚尾性等特征进行详细刻画,也使得度量结果更加精准。GED分布又可称作广义误差分布,其密度函数表达式为:
式(4)中,Γ(x)为伽玛函数,η为GED分布的自由度,当η=2时,GED分布即转为正态分布,当η>2时,GED分布表现出比正态分布尾部更薄的特征,当η<2时,则表现出比正态分布尾部更厚的特征。
在假设干扰项ε服从GED分布的前提下,对于CoES指标的估计可以分为以下三个部分进行描述。
1.各大银行VaR大小的估计
由式(1)可知,计算CoES指标的前提,需要先计量出银行i的VaR大小。因而对于银行i,参照高国华和潘英丽(2011)对银行个体的VaR的估计,我们对ARMA(1,1)-EGARCH模型中的均值方程进行修改①,同时我们参照Nelson(1991)对EGARCH的设定,对条件方差方程进行一定的修正,进而对个体银行i建立以下回归方程:
外,代表RMt时刻的市场收益率,DMt表示t时刻的市场收益的30d滚动方差,加入这两指标有利于提高方程拟合程度。特别的,方差方程中β反映了外部冲击带来的杠杆效应。
在GED分布下,进行极大似然估计后即可得出式(6)和(7)的系数,进而可以求出个体银行的在险价值VaRiq,t:
其中,是利用以上模型估计出来的银行预期收益率,是利用迭代的方法计算出的日收益率标准差,Z为扰动项服从GED分布下的q分位数。
2.超临界损失收益率序列模拟
根据CoES指标的定义,我们需要在各个银行i的收益率小于或等于VaRiq,t的时候,来求出此场景下的系统收益率的期望。因此,借鉴个体银行的在险价值的VaRiq,t估计方法,我们给出超出分位数临界点的该部分收益率序列Reiq,t的模拟思路:
其中,Z_excessiq,t是超额损失在收益率序列中的发生概率qeccess所对应的分位数,满足Z_excessiq,t≤Ziq,t。由于Z_excessiq,t在已知分布参数值及概率qeccess可得出,在此我们假设qeccess为均匀分布下生成的随机数,满足条件0≤qeccess≤q。
3.基于超临界损失收益率序列的CoES估计
首先,对于整个银行系统我们同样建立ARMA(1,1)-EGARCH模型:
最后,通过式(2)和(3)即可算出各银行对应的系统风险贡献度,并可以在不同银行之间进行比较,得出银行系统重要性排名。
三、实证结果分析
本文选取个股的股票收益率作为单个金融机构系统风险贡献度的测算基础。具体而言,参照田国强等(2019)设定①,在估计下行ΔCoES时,以商业银行的后复权收盘价来计算其日收益率,同时以中证沪深300商业银行全收益指数收盘指数作为银行系统收益率。其中日收益率序列计算如下所示:
Rt= (1nPt-1nPt-1)×100%(14)
其中,Rt表示第t天的收益率,1nPt和1nPt-1则表示相邻两个交易日收盘价。
本文将选取代表性银行的系统风险贡献度进行估算,并对系统重要性排序。为保证估算的准确性,我们将尽可能考虑所有上市的国有商业银行、股份制银行及主要的大型城商行。经过筛选,本文的研究区间确定在2011年1月4日—2018年12月28日,共1946个交易日,数据来源于Wind数据库。而对于系統重要性排序,我们将选取共计16家上市商业银行进行对比②,因16家商业银行资产占中国银行业资产总额比例约75%,故选取该样本分析的代表性较好。
(一)收益率序列描述性分析
为刻画收益率数据的特征,我们对银行指数及各大银行收益率进行了描述性统计分析,同时为保证收益率数据平稳,还对其进行了单位根检验(见表1)。各大银行的日收益率的偏度系数为均不恒等于0,因而收益率分布略有左偏或右偏,具有轻微的非对称性;由于峰度系数也远大于正态分布对应的系数3,故具有尖峰厚尾特征;J-B统计量更是达到3600.996,远大于正态分布所对应0.01显著性水平下的临界值9.21。综上,可以拒绝收益率分布满足正态分布的假设。同时,在对单位根检验后可知,所有收益率序列均在1%的水平上显著,即拒绝收益率序列存在单位根的原假设,收益率序列平稳。因此,采用GED分布下的ARMA-EGARCH模型来拟合收益率序列,并估计CoES模型有其合理性。
(二)商业银行系统重要性衡量
通过建立ARMA(1,1)-EGARCH模型对收益率拟合,我们可以计算出各大银行的动态ΔCoESL,通过绘制图形(见图1),进而可以观测各大银行系统风险贡献度变化趋势。可见,大多数商业银行的系统风险溢出水平均在2015年及2018年的经济波动期间达到峰值,这也充分体现了系统风险的负外部性及传染性。此外我们观察到,国有大型商业银行的系统风险贡献度尽管较高,但除去危机期间,从长期看其变动幅度相对较小。而股份制商业银行和城市商业银行的系统风险溢出水平虽相对较低,但其波动较大,说明其在日常经营中更容易受到内外部冲击因素的干扰,自身稳定性较差,也就更容易向整个银行系统中发出冲击,在正常经济运转情况下,更容易成为整个系统中的不稳定因素。
由于银行的系统风险贡献度大小同时是反应商业银行的系统重要性的重要依据。此处,我们以标准化后的%ΔCoESL及式(10)中的长期风险溢出系数作为依据,对各类商业银行的系统重要性进行比较(见表2)。
由表2可知,国有制商业银行短期收益率波动对于银行系统的风险溢出最大,国有制商业银行的系统重要性最高,其中中国工商银行对银行系统影响最大。因而危机发生时,应当优先关注五大行的稳定性,特别注意对中国工商银行的风险防控。此外,我们也注意到,股份制商业银行和区域商业银行中也不乏有对系统有较大影响的银行,如中信银行、北京银行、宁波银行等。
反观长期风险贡献度指标,银行个体表现出较强的个体差异。大型商业银行中最应加以持续关注的是中国建设银行,其单位自身风险能造成65.9%的风险溢出;北京银行应作为城商行中的重点监管对象;股份制商业银行中,招商银行的系统风险贡献度则远超其余股份制银行,这可能与招商银行长期以来在规模上的领军地位以及复杂的业务往来有关。
四、系统风险贡献度的影响因素
在对银行系统风险贡献度进行度量之后,本文还试图寻找对该种溢出效应变动起作用的影响因子。正如前述文献所言,尽管基于宏观变量和资产负债表的指标法在度量系统风险时存在诸多不足,近年来也并非主流的测度方法。但循着这一研究思路,我们可以将系统风险贡献度的起因分为两类研究:即微观主要基于资产负债表个体特征的诱因以及宏观经济层面的影响因素。通过回顾有关文献,在微观方面,金融机构机构的规模、杠杆、流动性、盈利水平和资产质量仍然是最为广泛讨论的影响因素;在宏观影响因素可以从货币政策、经济景气程度、经济放开程度三个视角进行研究。
此处,本文将采用上述16家上市银行2011—2018年的季度财务数据和相应季度宏观数据,结合面板回归模型对银行系统风险贡献度的影响因素进行分析,具体回归方程设置如下:
表3)。
(一)面板数据描述性统计
在进行面板回归之前,我们首先应对以上变量进行描述性统计,并进行单位根检验,防止非平稳数据导致的伪回归现象(见表4)。其中,不良贷款率(npl)是一阶单整,其余变量序列均在5%的显著性水平上平稳。因此,在后续回归中,对不良贷款率进行差分处理。
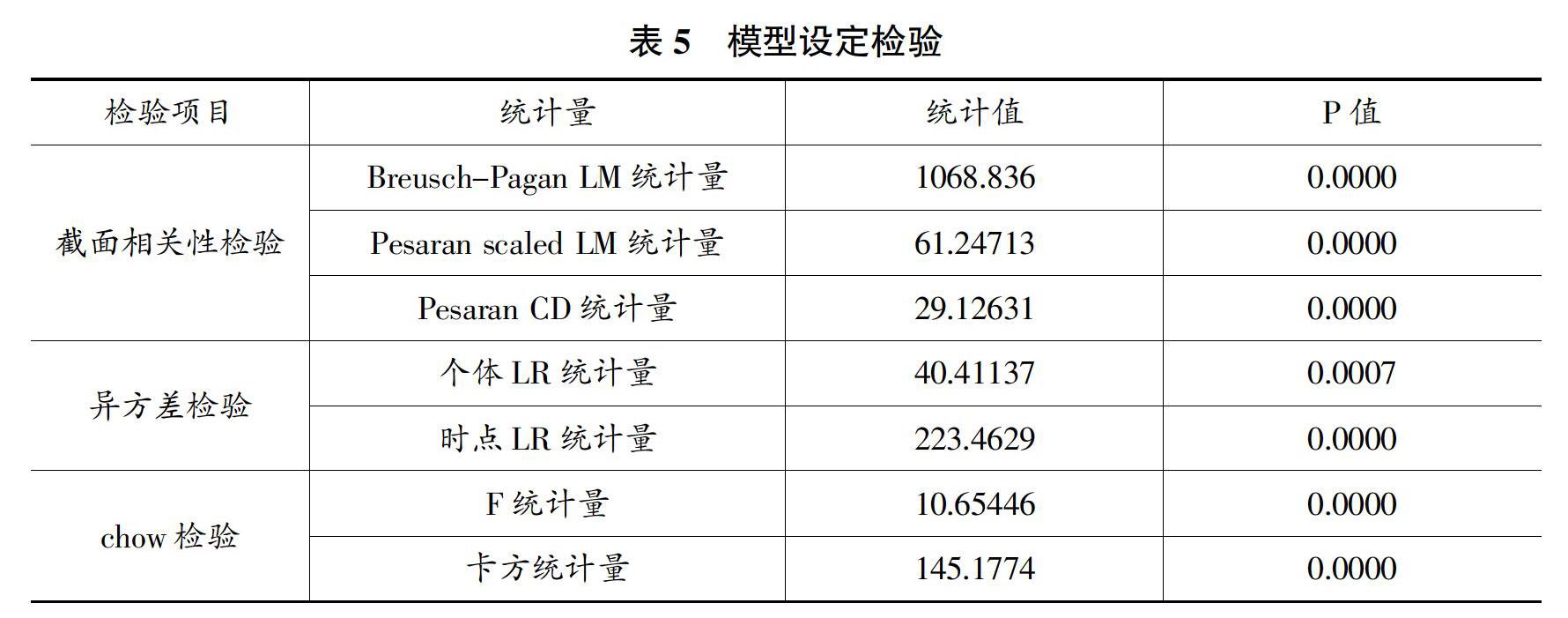
(二)面板模型相关检验
在利用式(15)进行回归时,还需要进行残差截面相关检验及异方差检验,同时应判断应当采用固定效应还是随机效应模型。由表5可知,残差在1%的显著性水平下拒绝个体不存在相关性和同方差假设,即残差截面相关且存在异方差。因而在估计权重时,利用相应的广义最小二乘估计进行调整,并采用white截面方法作为系数协方差估计方法。根据chow检验的F统计量及卡方统计量,同样在1%的显著性水平上拒绝原假设,即模型存在个体固定效应。
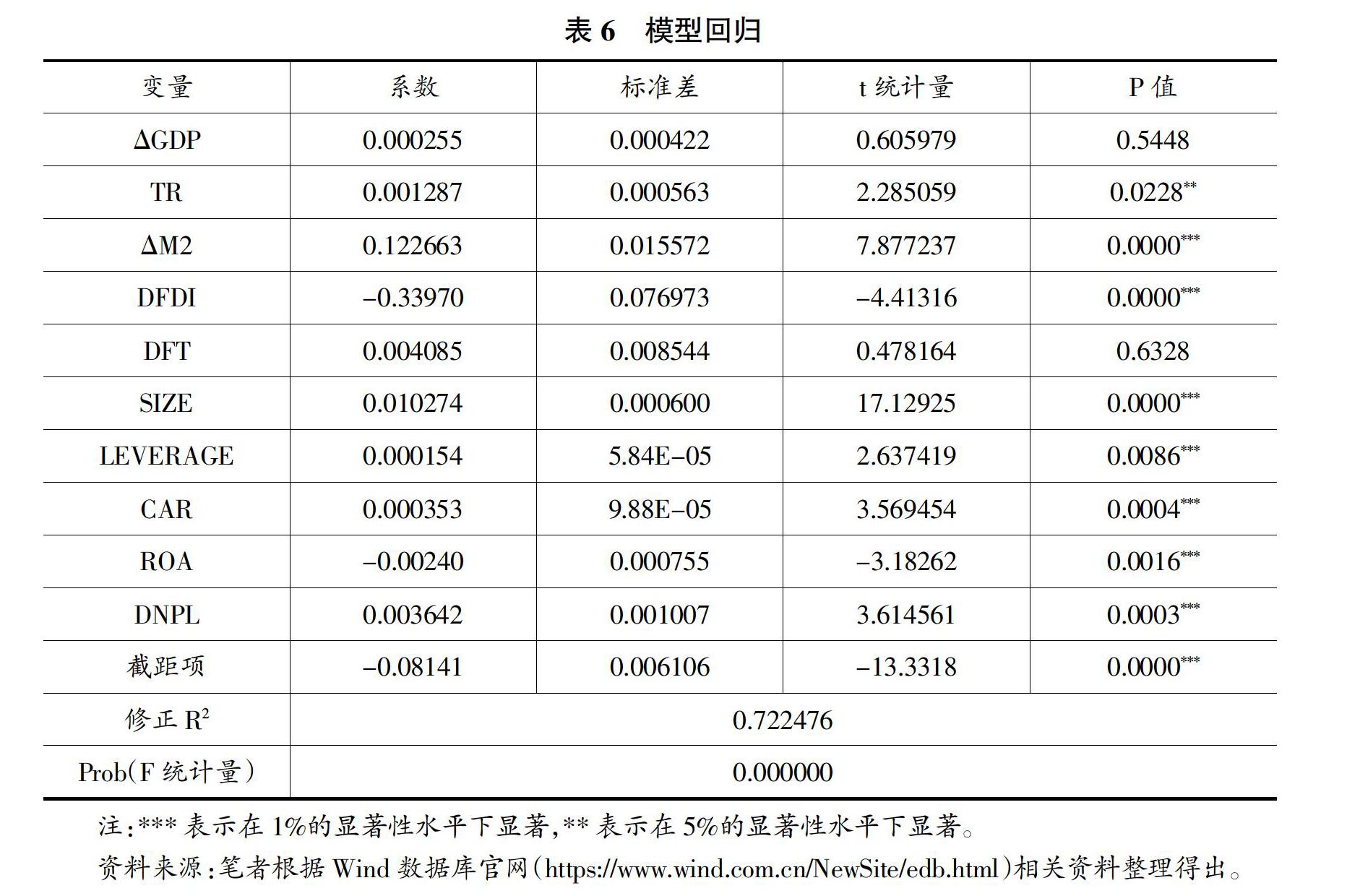
(三)面板模型回归结果
建立固定效应面板数据回归模型,回归结果见表6。可以看出十个解释变量中, M2增长率、对外投资依存度、市值规模、权益乘数、资本充足率、总资产收益率、不良贷款率在1%的显著性水平上显著,期限利差则在5%的水平上显著,而GDP同比增长率、对外贸易依存度则不显著。
具体而言,国债期限利差越大,银行系统风险贡献度上升。这是由于利差扩大意味着人们要求更高的流动性溢价,来补偿未来将面临的更大的流动性风险,进而使得银行的风险传染的可能性增大。
广义货币增长率的上升,将会带来银行系统风险贡献度上升。这说明了宽松的货币政策鼓励银行进行风险承担。同时与期限利差影响相比较,其系数更大,影响也更为显著,说明了银行风险承担行为对于数量型货币政策调整更为敏感,这也与我国货币政策主要采取数量型工具的事实相符。
对外投资依存度增加,系统风险溢出影响下降。考虑到双向投资在经济中占比增加,将有利于从竞争模仿等途径,促进技术、资源、人员素质等要素决定的经济高质量增长,同时,伴随越来越多的企业采用新设具有法人资质的子公司的形式对外投资,这一方式提高收益降低成本的同时,还起到多元化经营分散风险的作用,而境外法人独立担责又减少了外部风险向国内传递,最终使得企业也高质量增长。双重作用下,银行的坏账概率大大降低,资产质量上升,进而系统内银行对于外部的风险溢出下降。
此外,GDP同比增长率ΔGDP与对外贸易依存度DFT尽管影响不显著,但二者仍与系统风险贡献正相关。这表明经济增长较快时期,银行倾向于有更多风险承担行为,其对系统的潜在溢出风险积聚。而贸易往来越频繁,对外贸易依存度越高,关税等贸易壁垒使得国内经济波动的可能性越大,传导至金融市场使得银行系统的稳定性也越差。
从微观个体变量来看,市值规模的系数显著为正值,且在个体影响因素中,其对系统风险溢出程度的贡献最大。这恰是对规模越大的银行,一般系统重要性越高的解释,也印证国内银行系统存在“太大而不能倒”这一现象。
权益乘数代表的财务杠杆与不良贷款率的增量与系统风险溢出程度也呈现出正相关关系。由于高杠杆及不良贷款率上升都会使得商业银行面临较高的信用风险,根据前述系统风险传导渠道,当企业违约事件频发,银行的信贷将会萎缩,由于高杠杆的存在可能存在资不抵债,进而抛售资产的情形,使得資产价格降低,进而风险在整个系统中传播开来。因而高杠杆及不良贷款率上升均会导致银行系统风险溢出增大。
衡量银行流动性的资本充足率的回归系数为负,这一点与过往经验并不一致。一般而言银行流动性越高,其经营过程中安全性越高,但过高的流动性并不利于银行风险的降低。如较高的资本充足率说明银行对于资本的利用并不充分,资产端业务并未得到全面发展,使得其盈利能力较弱,不利于其持续经营。我国银行业目前对于资本充足率的监管的基本要求是10.5%,样本测试中16家银行远超这一指标,国有大型银行的资本充足率普遍在15%这一水平,存在一定的效率损失,反倒可能不利于限制风险外溢。
在个体银行的盈利方面,总资产收益率ROA的回归系数显著为负。这说明银行个体的盈利能力越强,其系统风险贡献度越弱。这是由于其具有较强的能力抵御外部冲击和内部风险,发生破产或财务困境的概率较小,不易使得自身风险向外部传递,进而使得其系统风险贡献度较低。
总体而言,除去对外贸易依存度及总资产收益率外,其余指标与系统风险贡献度均呈正相关关系。因此在实践过程中,监管机构应当注意在经济增速较快、期限利差扩大、货币供应量增加、双向投资骤缩及贸易往来频繁等时期,对规模较大、财务杠杆较高、资产质量较差、流动性过高、盈利水平较低的商业银行进行重点监管。
五、结论及建议
(一)结论
本文基于Adrian&Brunnermeier(2016)提出CoES方法,借鉴李政等(2019)对这一方法的改进,利用ΔCoESL指标对其系统风险贡献度进行度量,并以标准化后的指标%ΔCoESL对16家上市银行的系统重要性进行比较。在此基础上,本文进一步从宏观和微观两个角度入手,通过面板回归探讨了影响系统风险贡献度的因素,得到以下结论:一是国有大型商业银行的系统重要性普遍高于股份制商业银行和城市商业银行。其中,中国工商银行的系统重要性在所有银行中最高,而中信银行系统重要性位列股份制银行之首,城商行中则是北京银行的系统重要性最强。二是期限利差越大、宽松货币政策、较大市值规模、较高财务杠杆、过量流动性以及不良贷款率剧增都会显著引起银行系统风险贡献程度加大,较高的对外投资依存度及总资产收益率会显著降低银行的系统风险溢出效应。另外,较快的国内生产总值增速和对外贸易依存度,可能导致银行的系统风险传染性增大。
(二)建议
一是监管机构在考虑传统评价指标(如机构规模、关联度、复杂性、可替代性、资产变现等)的同时,还应充分发挥数据挖掘功能,建立系统风险贡献度实时评估模型和预警模型。二是在中美贸易战背景下,监管机构应当密切关注外部环境变动中可能对银行系统稳定性造成影响的因素,包括国内经济增长、涉外投资及贸易及货币政策等。三是在现行金融监管双峰模式下,无论是人民银行的逆周期宏观审慎政策和银保监会的微观审慎监管,亦或是审计机关贯彻的全面风险管理框架,既应注意差异化监管,也应注意适度监管的问题。从长远看,监管过严不仅使银行丧失创新活力,损失效率,还会使其资本运用不充分,进而降低盈利能力,抵御内外风险能力下降,无法保证长期稳定经营,进而可能引发范围更为广泛的系统风险溢出。
(责任编辑:孟洁)
参考文献:
[1]李政,梁琪,方意.中国金融部门间系统性风险溢出的监测预警研究——基于下行和上行ΔCoES指标的实现与优化[J].金融研究,2019(2):40-58.
[2]上海财经大学高等研究院“中国宏观经济形势分析与预测”课题组.中国银行系统稳定性研究[J].中国经济报告,2019(2):110-117.
[3]张冰洁,汪寿阳,魏云捷,赵雪婷.基于CoES模型的我国金融系统性风险度量[J].系统工程理论与实践,2018,38(3):565-575.
[4]朱波,卢露.不同货币政策工具对系统性金融风险的影响研究[J].数量经济技术经济研究,2016,33(1):58-74.
[5]白雪梅,石大龙.中国金融体系的系统性风险度量[J].国际金融研究,2014(6):75-85.
[6]刘生福,李成.货币政策调控、银行风险承担与宏观审慎管理——基于动态面板系统GMM模型的实证分析[J].南开经济研究,2014(5):24-39.
[7]孙立行.开放条件下中国金融风险预警指标体系研究[J].世界经济研究,2012(12):30-37+85.
[8]刘吕科,张定胜,邹恒甫.金融系统性风险衡量研究最新进展述评[J].金融研究,2012(11):31-43.
[9]陈雨露,马勇.泡沫、实体经济与金融危机:一个周期分析框架[J].金融监管研究,2012(1):1-19.
[10]高国华,潘英丽.银行系统性风险度量——基于动态CoVaR方法的分析[J].上海交通大学学报,2011,45(12):1753-1759.
[11]周小川.金融政策对金融危机的响应——宏观审慎政策框架的形成背景、内在逻辑和主要内容[J].金融研究,2011(1):1-14.
[12]谢福座.基于GARCH-Copula-CoVaR模型的风险溢出测度研究[J].金融发展研究,2010(12):12-16.
[13]Acharya V V.A theory of systemic risk and design of prudential bank regulation[J].Journal of financial stability, 2009, 5(3): 224-255.
[14]Acharya V V,Pedersen L H,Philippon T,et al.Measuring systemic risk[R].Federal Reserve Bank of Cleveland, Working paper, May, 2010.
[15]Acharya V,Engle R,Richardson M.Capital shortfall:A new approach to ranking and regulating systemic risks[J].American Economic Review,2012,102(3):59-64.
[16]Adrian T,Brunnermeier M K.CoVar:a method for macroprudential regulation[J].Federal Reserve Bank of New York Staff Report,2009,348.
[17]Adrian T,Brunnermeier M K.CoVaR[R].National Bureau of Economic Research, Working paper,October,2011.
[18]Adrian T,Brunnermeier M K.CoVaR[J].The American Economic Review,2016,106(7):1705-1741.
[19]Banulescu G D,Dumitrescu E I.Which are the SIFIs?A Component Expected Shortfall approach to systemic risk[J].Journal of Banking & Finance,2015,50(1):575-588.
[20]Brownlees C,Engle R.Volatility,correlation and Tails for Systemic Risk Measurement[R].Social Science Reserch Network,Working paper,June,2011.
[21]Chan-Lau J A,Espinosa M,Giesecke K,et al. Assessing the systemic implications of financial linkages[J].Global Financial Stability Reviews,2009,2(6):73-110.
[22]張立华,张顺顺.宏观审慎框架下系统重要性银行风险评价及其防范路径研究[J].西南金融,2019(10).
[23]吴颂.农村商业银行系统流动性风险管理问题研究——以江西省抚州市为例[J].区域金融研究,2019(3).
[24]庞丽媛.商业银行创新业务风险分析及监管建议[J].黑龙江金融,2018(10).
[25]包蕾.我国金融控股集团模式下商业银行风险管理研究[J].北方金融,2018(8).

