数字PCB电流传导干扰信号检测的一种算法

刘阳

（湖南高速铁路职业技术学院铁道电信学院， 湖南 衡阳 421002）

0 前言

数字电子系统中，元器件的安装在印刷电路板上的密度越来越高，高速逻辑部件尤为多见。数字设备向外界辐射电磁干扰信号的主要噪声源[1，2]是印制电路板上的信号布线，

同时，它也很容易受外界干扰。其电流会随着逻辑开关的状态变化产生较大变化，同时有较多的高频谐波分量。这些高频谐波产生的干扰信号会干扰设备，进而造成电磁污染。故在数字电子系统设计和数字电子产品定型测试中，要对数字设备的电磁兼容（EMC）性进行分析。

进行传导干扰信号测试时，数据采集卡前端（或自带）的信号调理及其板卡布局、外界环境噪声等会造成输出中含有较大的噪声，消除这些噪声后才可以得到准确的结果[3]。

本文介绍了网格及网格分形模式，提出了一种用于短时分形维数的模糊行实时检测的算法。

1 电磁干扰检测系统

电磁干扰信号的自动检测系统在数字印制电路板中的具体实现原理如图 1所示。当测量分析印制电路板传导干扰时，线性阻抗稳定网络（LISN）必须在待测设备（ EUT: equipment under test ）与电网交流电源之间。首先，谐波源需要将输出的电流经过调理电路进行增益、调理、滤波并通过电压激励后送入数据采集卡，用来满足后续设备对输入端电平的要求，当然，有些情况下数据采集卡会自带调理电路；而后，核心电路开始工作，对i（或u）处理，将幅值在抽样时间内依然为连续的模拟信号经过转换变为数字信号，并将此信号X(n)送入存储器，当然，这两步的工作过程中由于内部和外部的原因，信号积累了一定的噪声。最后，开展基于短时分形维数的模糊控制滤波，消除噪声N(n)，得到S(n)，对其处理后做测量，并通过外设来输出结果，用来做分析和处理。

图1 电磁干扰检测系统图

2 网格与网格分形维数计算

2.1 网格与分形维数的算法

网格是一种用于集成或共享地理上分布的各种资源，使之成为有机的整体，共同完成各种所需任务的方式。一般而言用Xj来表示在n维空间nR 上的一个网格，Xj的直径为网格的尺寸△， Rn=UXj。显然，在这个集合中，包含多个△或称近似的△。当然，根据网格形状不同又可以把它们分为矩形网格、三角形网格和正方形网格等。

网格分形方式的实用性很强，计算机在做图像的数字化处理时也可以选用网格分形方式来进行，尤其是在复平面的迭代、分形云彩的模拟等方面。它简单实用的特点被发挥的淋漓尽致。本文以正方形网格为例做分形。现就网格分形方式做简单分析，处理过程如下文所述。

用尽可能细(小)的△正方形网格将n维空间上的 Rn划分，将集合X做离散处理，变成数字点集NΔ，即为集合X的点计数。接下来我们做放大处理，把较小的△网格放大，变为以kΔ为宽度的正方形网格，同理用NkΔ代表集合X 的点计数。容易得出，如果k的取值足够大，是可以达到 NkΔ＞1的条件的。在此条件下，使 Xk=ln k， yk= lnNkΔ，其中 k=1,2,···,K 。不难发现，在极限条件Δ→0时，可得

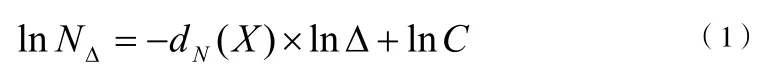
上式中，C为常数。接下来我们对集合X的网格分形维数dN(X)作简单数学处理后，可将其表征为：

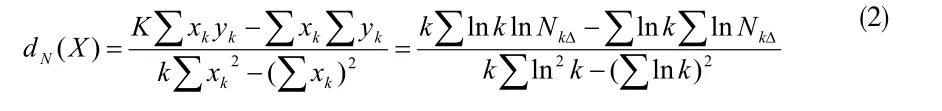
不难发现，在已经确定当前点间间距△（或称分辨率）时，l n NkΔ作为lnk的函数，它既是凸函数，还具有单调下降的特性，由此不难得到dN(X)的近似结果为

2.2 短时分形维数及其算法

确定其网络分形维数时可用一段数字印制电路板传导干扰信号作为函数图像。现将其做离散处理，将传导干扰信号抽样频率设为300kHz。为了研究方便毎帧选 128个抽样点、帧长 16ms，帧频 62.2。 那么对于第k帧而言，可以用

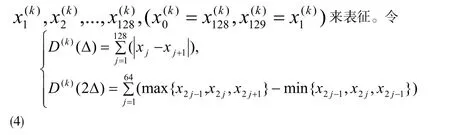
短时分形维数在各帧帧长趋向于零时可变成分形维数分布。在同等条件下，与采用短时Fourier变换来研究传导干扰信号不是平稳信号的情况一样，信号也可以应用短时分形维数来衡量其变化并能更有效的体现信号变化过程中出现的一些特征以提供做具体分析[4]。可见，滤波时是完全可以使用本算法的。

应用本算法（短时分形维数的其中一种算法）进行滤波时，如果需要尽量保持信号的基本特征，需要将短时分形维数变小；如果仅只是为了消除噪声，可将短时分析维数变大即可，可以根据实际需求作设置。实际设置时，需要注意的是模糊控制参数（用A表示）与短时分形维数(用B表示)基本关系可以表征为A变大则B变小，A变小则B变大。