永磁同步电机初始位置定位策略仿真分析

肖海峰

（西安航空学院 电子工程学院，西安 710000）

永磁同步电机通常应用于高精度运动控制场合中，控制系统对电机的动态响应及位置定位要求很高。因此，永磁同步电机的位置快速精准控制是伺服系统性能的重要指标，电机位置精准控制的前提是电机初始起动位置的辨识[1-2]。

通常情况下，永磁同步电机初始位置的检测分为3种方法：①利用绝对值编码器或辅助器件得到转子绝对位置，这种方法成本较高；②利用电机的空间凸极效应，通过向绕组注入短暂高频电压信号，根据响应电流来计算转子位置信息[3-6]。基于注入高频电压进行初始位置检测的已有方法对电机参数依赖性强，且需要利用锁相环或观测器等方法提取电流相位以计算转子位置信息[7-8]，算法都较复杂，转子位置信息易受到干扰而不适合实际应用。或者利用磁饱和特性给电枢绕组施加相同幅值、不同相位的电压矢量，当电压矢量和转子位置一致时，直轴电流响应幅值最大。通过观测直轴电流响应判断电机初始位置[9-12]，但是该方法电流检测电路要求较高；③通过检测三相绕组的电压或者电流来计算转子位置，该方法的本质是基于电机反电动势实现的，也需要精确的电流采样[13-14]。

本文提出了一种借助普通光电编码器实现永磁同步电机转子磁极初始位置的初步辨识的方法，该方法利用编码器U、V、W信号获取转子磁链初始位置所处的空间矢量扇区，根据扇区给定初始电压信号使电机起动，给定电压信号随着扇区的变化而变化，当Z信号被检测到对转子初始位置估计误差进行补偿。该方法能准确检测到转子磁极的位置信息，同时满足电机从静止状态起动的要求，且实现简单。

1 永磁同步电动机数学模型

在dq坐标系中，永磁同步电机的电压方程为[15]

式中：D 为微分算子；R 为定子电阻；Ld、Lq为 d、q 轴电感；ωr为转子电角速度；ψf为永磁体磁链。

旋转坐标系下的电机定子磁链方程为

旋转坐标系下的电机电磁转矩方程为

2 永磁同步电机初始位置定位策略

永磁同步电机通常采用普通增量式光电编码器，在电机启动前，通过码盘输出U、V、W信号可以估算出电机磁极所在的扇区位置，但并不能给出准确的转子位置信息，编码器输出的A、B、Z是用于控制电机的3个脉冲信号，其中A、B信号判断电机转速及方向，Z是同步信号，用来消除干扰脉冲或丢失脉冲对位置计数器造成的累积误差。

若采用的永磁同步电机的极对数为N，编码器分辨率为M线，经数字信号处理器DSP内部的QEP电路四倍频后，电机转子空间位置的分辨率变为4M脉冲/转。根据矢量控制原理，在每一个电周期内，6个矢量扇区循环一次 （CCW：011-001-101-100-110-010-011；CW：011-010-110-100-101-001-011），每个扇区对应电角度的范围为［N/6］。因此，在每一个电周期内，6个电压矢量V5（001）、V1（101）、V3（100）、V2（110）、V6（010）、V4（011）分别对应的电角度的数字量为［N/6］、［N/3］、［N/2］、［2N/3］、［5N/6］、［N］，扇区、电角度和机械角的位置关系如图1所示。

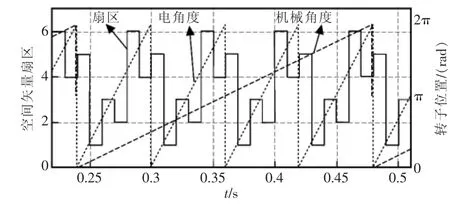
图1 电压矢量扇区与转子位置关系Fig.1 Voltage vector sector and rotor position relation

第一步根据码盘输出地U、V、W信号确定电机转子磁性所在的扇区，取该扇区中间位置对应的数字量作为转子初始位置，定转子磁链及电压矢量位置如图2所示。

图2 定转子磁链及电压矢量位置Fig.2 Rotor flux and voltage vector position

转子位置与紧邻的电压矢量位置的电角度差值范围为±π/6，其对应的数字量约为±［N/12］，系统按照矢量控制要求给定电机参考交轴电压矢量，电机有正向旋转的运动趋势，编码器反馈信号提供给位置信息作为电流环反馈位置输入，电流调节器输出电压矢量经逆变器在电机电枢上形成感应磁链与转子磁链相互作用并将转子咬合在初始位置上，但该位置并不一定是电机转子真实初始位置，而仅仅实现了电机转子位置的初步定位，此时电机输出的电磁转矩略大于准确定位时输出的电磁转矩，有利于缩短电机起动的暂态过程，当编码器输出的第一个Z信号到来之后，触发位置误差补偿算法，从而消除初始定位的相对误差，即可以准确定位转子位置。

3 仿真分析

为了验证文中提出的永磁同步电机初始位置定位策略的有效性，利用Matlab软件进行仿真实验。仿真所采用的永磁同步电机参数：额定功率1.5 kW；额定转速2500 r/min；永磁磁链0.182 Wb；极对数4对；交直轴电感5.33 mH；电枢电阻0.024 Ω；转动惯量0.0025 kg/m2。仿真分别给出了初始定位电角度误差30°和0°误差对应的电流过渡过程。

图3、图4给出了该永磁同步电机转子初始位置最大误差定位和理想定位下的电机起动电流瞬态过程。其中，在转子定位位置出现最大误差情况下，电机进入稳态所需要的时间小于0.25 s，起动过程优于转子位置定位误差为零的理想状态。其原因在于转子位置误差导致电枢感应磁链与转子磁链未实现完全正交，引起较大的起动电流，增加了电磁转矩。同时，由于转子位置误差使电压矢量在不同扇区间切换时出现了短暂的不确定过程，但根据相电流波形确定其影响可忽略，如图5、图6所示。当编码器输出的第一个Z信号到来之后，位置误差补偿算法在控制系统的一个控制周期内完成，转子初始位置误差得到准确补偿且过渡过程短暂，不影响电机的运行状态。补偿后的电机相电流略微减小，此时电枢感应磁链与转子磁链实现完全正交，电压矢量在不同扇区间切换时出现的短暂不确定过程同时消失。

图3 初始电角度误差为0°时电流瞬态过程Fig.3 When the initial electric angle error of 0°current transient process

图4 初始电角度误差为30°时电流瞬态过程Fig.4 When the initial electric angle error of 30°current transient process

图5 位置补偿前后的电机相电流波形Fig.5 Position compensation before and after the motor phase current waveform

图6 位置补偿前后的电压矢量扇区Fig.6 Position compensation before and after voltage vector sectors

4 结语

本文提出了一种永磁同步电机初始位置检测的方法，并从理论、仿真两个方面进行分析和研究，该方法利用普通编码器U、V、W来进行初始位置检测，克服了依赖电机参数或需要额外的硬件等缺点，算法易于实现，是一种鲁棒性较好的方法。仿真验证了电机转子在检测过程中不发生移动，即使检测误差达最大30°时也可以在最多不超过一个机械周期内实现误差补偿，满足永磁同步电机平稳、可靠起动的要求。