卫星导航信号捕获的一种高效相关算法

戴志春, 刘文祥, 封欣, 孙广富

(1. 国防科技大学 电子科学学院,湖南 长沙 410073;2. 中国人民解放军32021部队, 北京 100094)

0 引 言

信号捕获是卫星导航接收机数字处理首先进行的环节.信号捕获为了完成伪码相位和多普勒频率的时频二维搜索,需要将整个不确定范围划分成若干搜索方格,每个搜索方格对应着特定的码相位偏移量和多普勒频率偏移量.接收机根据该搜索方格的偏移量生成本地信号,并与接收信号进行相关处理.当相关值超过设定的捕获门限时,就判定信号存在,此时即完成了导航信号捕获,也即本地信号与接收信号的初始同步,并以此作为跟踪的初始条件[1].

卫星导航信号捕获是包括相关、搜索、判决等多个环节的复杂过程,其中检测概率与计算复杂度是衡量捕获算法性能的关键指标.在时频搜索间隔一定的条件下,决定检测性能和计算复杂度的最关键环节就是信号相关环节[2].因此卫星导航信号捕获相关环节的处理算法已经得到广泛而深入的研究.

对于二进制相移键控(BPSK)信号而言,其相关算法均采用匹配滤波,因此研究重点在于搜索间隔对相关处理性能的影响.不同于BPSK信号,二进制偏置载波(BOC)信号的自相关函数存在多峰特性,为了解决捕获时相关峰底部导致的漏检,提出了多种相关层算法,具体包括匹配滤波[3]、副载波相位消除[4]、双边带法[5]等.

目前几乎所有的卫星导航接收机均是基于数字电路实现,其中信号捕获的相关层实现在整个接收机的硬件资源中占据了重要的比重.因此信号捕获相关算法的高效实现对接收机的低功耗和低成本设计具有重要的意义.但是目前的文献主要关注捕获算法的理论性能,而较少关注相关算法在数字电路中的高效实现.

为了能够结合数字电路的特点对卫星导航信号捕获相关算法进行优化,论文首先介绍了信号捕获的三层分析模型,并在此基础上提出了一种高效的相关算法,最后比较了所提算法和传统算法的性能差异.

1 信号捕获的三层分析模型

卫星导航信号的捕获是包括相关、搜索、判决等多个环节的复杂过程.为了能够清晰地描述论文所提出的高效相关方法在整个捕获过程中的地位,下面介绍信号捕获的三层分析模型.

卫星导航信号的捕获本质上是信号功率、码相位延迟、多普勒频率和载波初相等参数均未知条件下的信号检测问题[6],即:

(1)

式中:H0和H1分别表示信号不存在和存在两种假设;r(t)为接收信号;C为信号功率;c(t)为调制的测距码;τ0为码相位延迟;f0为标称频率;fd为多普勒频率;θ0为载波初相;n(t)为噪声.

根据统计信号处理的经典理论可以得到上述二元假设检验的最大似然比检验为[7]

(2)

根据式(2)可以得到最大似然比检验准则下的最优检测量为

(3)

式中，v表示各种码相位和多普勒频率下的本地信号与接收信号的相关累加值,其表达式为

(4)

由式(4)可知,该检测量需要遍历所有可能的码相位和多普勒频率.但由于码相位和多普勒频率是连续的,受硬件资源和捕获时间的限制,实际接收机通常采用伪码相位和多普勒频率二维步进搜索的方法.二维步进搜索的实现示意图如图1所示[8].

接收机首先根据某一搜索方格的码相位和多普勒频率偏移量产生本地复现信号,计算复现信号与接收信号的相关值;然后遍历所有搜索方格,得到每个搜索方格的相关值;最后根据所有这些相关值进行信号是否存在的二元假设检验.因此二维步进搜索过程可以分为如下三层[9]:

1) 相关层:根据输入信号r(t),计算得到某方格(i,j)的相关值Vi,j;

2) 搜索层:根据设定的二维搜索间隔,遍历所有方格,得到相关值矩阵V;

3) 判决层:根据相关值矩阵V,得到检测统计量T(V),并与门限比较,进行二元判决.

根据上述的三层分析模型,论文主要研究的是当相关层算法确定之后,基于数字电路架构如何高效地完成相关值Vi,j的计算.

2 一种高效的相关算法

在数字接收机中,信号捕获相关层中最基本的运算是基带信号与本地伪码的相关累加运算,其表达式为

v=∑r0[k]*c[k].

(5)

式中：r0[k]表示经过相位旋转后的基带复信号,c[k]表示生成的本地伪码.

为了提高捕获速度,目前接收机均使用并行捕获算法,其实现结构主要由大规模的并行相关器和加法树组成,具体如图2所示.

通常单次累加的点数N选为2的整数倍,假设N=2(M+1),则整个加法树共M级,第i(i=0～M)级包括N/2i个(i+1)bit加法器.当单次累加点数较多时,加法树就成了影响相关层所需硬件资源的重要因素.

从减小硬件资源的角度考虑,基带信号使用1 bit量化所需的硬件资源最少.但是在宽带接收条件下,1 bit量化会引入约2.5 dB的性能损耗[10].综合硬件资源和性能损耗两方面,传统的相关层实现算法中,基带信号使用2 bit表示,0、±1共3电平量化,可量化损耗降低至约0.9 dB[10].但由于加法树的输入位数变为2 bit,所需的硬件资源约是1 bit加法树的4倍.

为了降低基带信号使用2 bit量化时加法树所需的硬件资源,论文提出了一种高效的相关算法.

在论文所提算法中,使用±1和±3共4电平量化,在保证均匀量化的同时,可保证量化后均值为0.由于使用了2 bit的全部4个电平,相比传统的3电平量化,提高了有效位数,减小了量化性能损耗.同时为了能够使用异或完成相关累加计算,在使用2 bit表示4个电平时采用了如下的编码规则:

1)bit0的0表示1,1表示-1;

2)bit1的0表示2,1表示-2.

具体的量化和编码规则如表1所示.

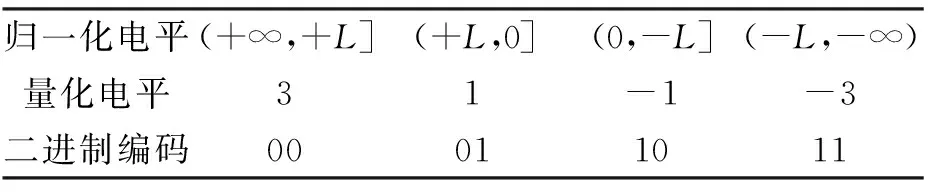
表1 高效相关算法的量化和编码规则

表1中,L为量化门限,通常与输入信号的标准差相关.通过采用上述量化及编码规则,可以通过异或的方式实现2 bit基带信号的相关累加,具体计算方法如下:

1)所有基带信号的bit1与本地伪码异或后累加,得到v1;

2) 所有基带信号的bit0与本地伪码异或后累加,得到v0;

3)最终的相关累加结果为2v1+v0.

上述高效相关算法对应的实现结构如图3所示:

由上述计算方法和实现结构可知,论文所提的高效相关算法通过采用特殊的量化和编码规则,在保证计算结果等价的条件下,将传统的2 bit加法树转化成2个独立的1 bit加法树.

3 性能分析

论文所提的相关层高效算法与传统算法的主要区别在于硬件资源和量化损耗,下面分别分析.

3.1 硬件资源

由前面的介绍可知,论文所提的高效相关算法与传统算法在硬件资源方面的主要区别如表2所示.

表2 论文所提算法与传统算法之间的硬件资源比较

由上述对比可知,论文所提算法和传统算法的相关器使用资源几乎相同,主要区别在于加法树的实现.虽然论文所提算法中加法树每级加法器的数量是传统算法的2倍,但是加法器输入bit数少1,因此总的硬件资源约为传统算法的1/2,有效降低了信号捕获所需的硬件资源.

3.2 量化损耗比较

相比传统算法中仅使用3电平量化,论文所提的高效算法可使用4电平量化,这可以降低量化引入的损耗.由于难以对量化损耗进行理论分析,下面通过蒙特卡洛仿真的方法,比较论文所提算法与传统算法之间的差异.

蒙特卡洛仿真的实现框图如图4所示.

具体的仿真结果如图5所示.

由图5可知,使用4电平量化的最低量化损耗约为0.5 dB,相比3电平量化要少约0.3 dB.对应的最优量化门限约为0.75 σ.

4 结束语

论文针对卫星导航信号捕获中相关层的高效实现,结合数字电路的特点提出了一种高效的相关算法.相比传统实现方法,相关层加法树所需硬件资源可减小1/2,量化损耗减少约0.3 dB,对卫星导航接收机低功耗和低成本实现具有重要的参考价值.