采用包络-准则法优化考虑瞬态传热的薄板结构

孙 国， 阎 琨， 蔡贤辉， 程耿东

（大连理工大学 工业装备结构分析国家重点实验室 工程力学系，大连116024）

1 引 言

在工程结构中，薄板结构广泛应用于航空航天、机械和交通等领域，往往起着承载和隔断空间的作用，因此，弹性薄板结构分析及最优设计受到持续的关注。程耿东等［1－3］以薄板的柔顺性为目标函数，由变分原理出发，推导出优化准则，构造了求解板的优化厚度分布函数的迭代格式，以提高薄板结构的刚度。

在重要的工业装备结构中，受到高温的热结构失效往往会造成严重后果，其设计成为核心技术。即使是稳定的温度场，热荷载作用于结构时，一方面产生温度应力和温度变形，另一方面降低材料的很多力学性能，给结构设计带来很多困难，某些条件下增加材料用量使得结构内的热应力更大，而这和没有温度荷载的情况正好相反。热结构设计面临的这些特殊问题需要研究特定的设计方法。Rao等［4］基于温度边界用最优准则法设计，Adelman等［5］进行了热弹性的满应力设计，Haftka等［6］通过近似方法进行了耦合热结构设计，Tortorelli等［7］分析了热弹性问题的结构响应灵敏度等。近年多为以控制结构应力和位移为目标的拓扑优化研究。左孔天等［8］采用多目标优化方法进行传热结构的拓扑优化设计。Pedersen等［9－10］在结构柔顺性优化之后，增加一个启发式的应变能密度的均匀化过程，以处理局部应力过高的问题。张卫红等［11］用柔顺性和弹性应变能两种指标进行热结构拓扑优化设计，给出数值算例并指出应变能指标对于降低应力水平更为有效。倪晓琴等［12］推导了实心弹性薄板结构在温度荷载作用下的优化准则，有效地降低了板壳结构在稳态温度场下的热变形。

需要考虑瞬态传热过程的薄板结构优化设计更加困难，因为温度荷载不仅与时间有关，也与模型厚度相关，而在优化过程中厚度分布会不断修改，意味着不再满足前期一些优化问题假定的均匀稳态温度场分布，更为严重的是，如果叠加在结构上的温度应力变化范围很大，稳态优化设计结果在瞬态传热过程中可能出现较大的局部应力，需要建立非稳态温度场下的优化方法。Kok等［13］利用响应面方法进行瞬态热应力问题的优化求解；Turteltaub［14］提出了瞬态传热下对材料特性进行拓扑优化；Molaei Najafabadi等［15］进行了考虑瞬态传热过程的功能梯度材料的参数优化设计。本文对已有的稳态温度场下薄板的优化准则加以局部修正，以处理瞬态传热过程中的薄板结构优化问题。

2 瞬态温度场下薄板结构优化设计

2.1 只有外力作用下弹性薄板的最小柔顺性设计

图1为平面薄板结构，在平板中面上建立坐标面xOy，z轴沿中面法向，板厚h＝h（x，y）。

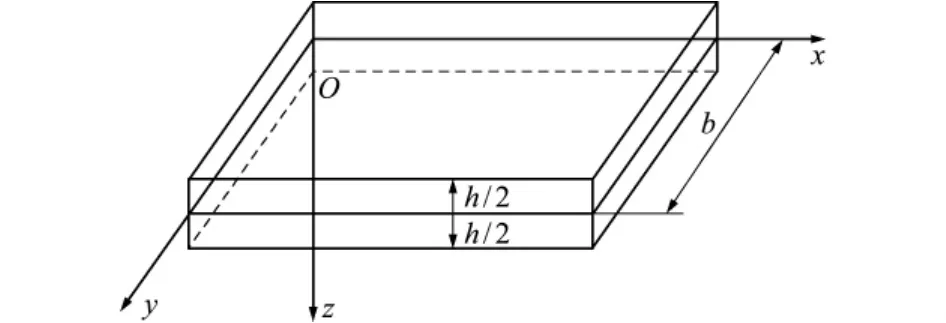
图1 薄板Fig.1 Thin plate

如果考虑薄板承受垂直于中面的机械荷载q的作用，通常将目标函数选取为结构的柔顺性：

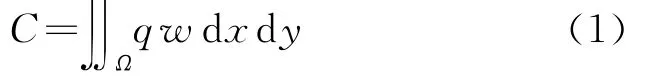
在单纯外力作用且无初始应力的条件下，式（1）给出的柔顺性正比于结构弹性应变能，如式（2）所示。

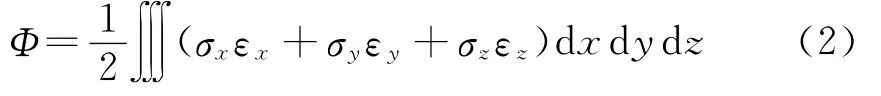
满足材料体积约束条件：

设计变量h（x，y）除了满足积分约束，还有最大最小限制hmin≤h（x，y）≤hmax。采用变分法可以得到该优化问题的最优条件如式（4）所示，具体推导不再赘述［1］。

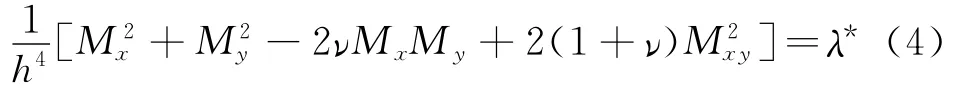
式中 Mx，My和Mxy为在截面单位宽度上的弯矩及扭矩，ν是泊松比，λ＊是拉格朗日乘子。

引入指标函数g（x，y）：

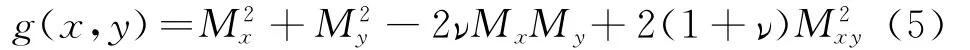
求解关于厚度h（x，y）的方程，优化条件可重新写为

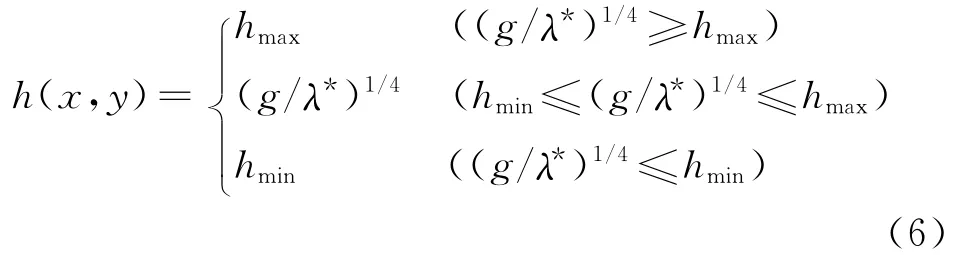
λ＊为优化问题的拉格朗日乘子，式（6）不能直接求出h（x，y），可以采用迭代形式求解。根据体积约束条件，可以解出拉格朗日乘子λ＊。

式中V为材料总体积，Ωu，Ωmin和Ωmax分别代表厚度取中间值、最小值及最大值的区域。

薄板弯曲最大应力出现在上下表面处，以上表面为例，

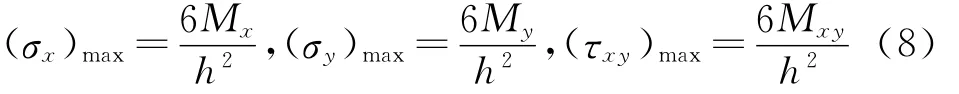
指标g（x，y）可以由表面最大应力表示，该值和板内各点的应变能密度有关，这一特点使得将厚度修改式（6）应用于受到机械力和稳态温度荷载联合作用的薄板的柔顺性优化设计中也很有效。

2.2 瞬态温度场下薄板结构优化设计

当考虑瞬态热-结构耦合问题时，假定结构受到的外力和热荷载是一个典型的准稳态过程，温度场按导热方程瞬态求解，应力场取不同时刻温度场，按稳态求解，忽略结构变形对温度场的影响。

从优化设计的角度来看，瞬态温度场T（x，y，z，t）的变化特性使得Mx，My和Mxy同样是随时间变化的，则稳态温度场下的优化准则难以适用，直接建立非稳态温度场下的优化准则同样十分困难。为了处理这种复杂分布的T（x，y，z，t），将一个考虑瞬态传热复杂温度荷载下的弹性薄板优化问题分成两个子问题，即控制挠度w的优化问题和控制局部热应力较高的问题。

基于已有的薄板优化有关研究工作，在单独外力q作用下，基于柔顺性的优化结果可以提高结构抗弯刚度，进而有效降低机械荷载q作用下的挠度w，温度荷载对于挠度w的影响主要源于温度弯矩MT的影响（面内热膨胀对于挠度w的影响可以忽略），这个基于柔顺性的优化结果仍然可以控制q和MT共同作用下的挠度。

为解决传热过程中出现的局部热应力较高的问题，本文给出一种包络-准则方法，对瞬态传热过程中高应力区域进行局部修改处理。考虑构造表征传热过程中多个时刻下g（x，y）最大值的包络函数G（x，y）和局部修正的权重函数W（x，y）。构造包络函数时间点的具体取值需要兼顾计算效率与包络函数的精度。针对一种常见的薄板结构单侧对流传热的瞬态过程，为了避免在后期接近热平衡的时间段内配置过多时间点，经验性地采用逐渐增大间隔时间点计算包络函数。考虑到具体选点方案对包络函数计算结果的精度是有影响的，针对初始设计模型，将拟采用的时间选点方案与相对密集选点方案计算结果相比较，以保证能有足够的精度。为实现局部修正，对于高应力区域，令W（x，y）近似等于1，其他位置则相对较小，修正后的指标量G（x，y）W（x，y）相当于在局部高应力区域采用了一个类似的指标量G（x，y），而其他应力较低的区域则不做修正。经过一定次数迭代，局部应力集中现象逐渐得到缓解。另一方面，进一步的迭代会使修正范围增大，由于包括了瞬态过程多个时刻的影响，迭代过程的收敛性和有效性不能严格保证，较大的修正范围可能导致设计结果出现劣化，因此这个局部修正迭代过程需要检查最大应力变化，并采用最优设计结果。

该包络-准则方法包括两个环节的优化设计。首先，针对外力荷载q，进行一个结构柔顺性的优化设计；以这一设计为基础，通过计算多个时刻指标函数g并取其包络，对其进行修正迭代，以消除瞬态温度场作用下的局部高应力。其具体步骤和有关公式如下。

（1）首先利用式（5，6）进行外力q作用下的优化设计，为方便表述，将这个优化环节称为OPT-1，其结果作为进一步考虑瞬态传热优化设计的初值。为了与温度荷载下的计算结果区分，将式（5）改写为下标q的形式。

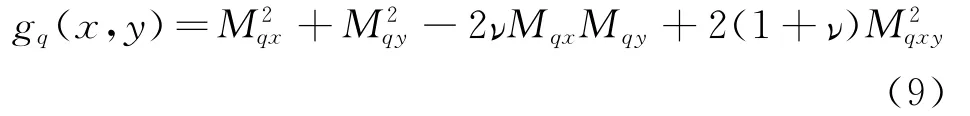
（2）为了在设计中考虑瞬态传热过程的影响，定义瞬态传热过程t时刻的指标函数gqT（x，y，t）值为

式中 下标qT代表载荷q和温度T联合作用，取gqT在多个时刻ti的值，并构造包络函数GqT为

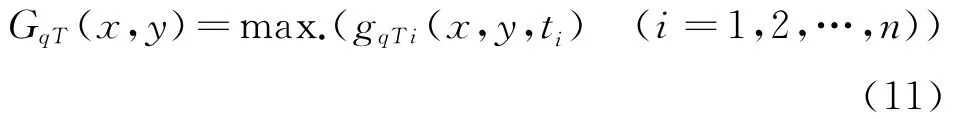
式中ti（i＝1，2，…，n）代表瞬态不同时刻。

（3）构造局部修正的权重函数W（x，y）

利用GqT计算对应的应变能密度SqT，

将SqT最大值归一化，构造表征应变能密度水平的权重函数W（x，y），

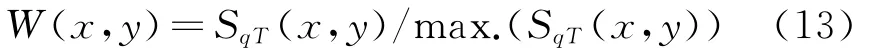
（4）通过对比两种状态下的指标函数gq（x，y）和G（x，y）W（x，y），实现瞬态过程中高应力区的局部修正，修正后的指标变量为

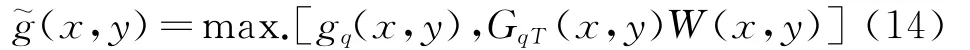
通过与式（6，7）类似的迭代计算，求解厚度h（x，y）。为方便表述，将这个优化环节称为OPT-2。

3 数值算例分析

如上文所述，包络-准则法优化包括OPT-1和OPT-2两个环节，OPT-2采用OPT-1设计结果作为初值。算例的主优化程序通过Matlab编程实现，调用ANSYS软件执行有限元模型修改和分析任务并输出计算结果数据文件，Matlab主优化程序进而读取这些数据文件，执行OPT-1或OPT-2优化计算，输出更新后的厚度数据文件，以供下一次迭代计算采用。

在OPT-2涉及的瞬态传热分析中，必须考虑沿厚度方向瞬态温度变化的影响，瞬态温度场分析采用在平面和厚度方向上具有传导热能力的层状壳单元Shell-131，为4节点单元，该单元适用于壳单元的稳态或瞬态热分析，计算生成的温度可以传递至壳单元进行热应力求解。应力分析采用Shell-181单元，为4节点单元，每个结点具有6个自由度，适合对薄壳到具有一定厚度的壳体结构进行分析。上述两种单元壳体厚度和积分点数量的设定可以在横截面的定义中完成。本文将shdll-131单元和shell-181单元都设定为3层，每层积分点数为3个，单元沿厚度共有7个积分点（因层间两处积分点重合），较多的积分点有助于保证分层计算的精度，但同时导致计算量的增加。将4个层面上的温度计算结果传递到shell-181单元，构成一个沿厚度的3层线性温度函数。

采用的材料特性为，弹性模量E＝200GPa，泊松比ν＝0.31，热膨胀系数α＝1.3E-5，导热系数k＝15.0W／m·K，比热容c＝450J／kgK，密度ρ＝8900kg／m3。

如图2所示为四边简支板，a＝b＝1.0m，根据对称性特征，取其1／4进行分析，均匀划分为2500个单元。给定下表面压力P＝100kPa，下表面对流换热系数hg＝250W／m2·K，环境温度TW＝500℃，外侧表面为绝热边界条件。结构初始温度T0＝0℃，壁板结构初始设计的厚度h0＝8mm，设计变量上下限为hmin＝2mm和hmax＝20mm。考虑到初始阶段温度变化较快，同时避免过大的计算负担，采用时间点取方案ti＝｛0，10，20，50，100，150，200｝（s），另采用较密集方案ti＝｛0，10，20，…，200｝（s）作为参照进行对比，G（x，y）计算结果分别记作单元向量形式和，以范数之比表征两者相对误差，‖G1－G0‖2／‖G0‖2＝0.66%，‖G1－G0‖∞／‖G0‖∞＝1.3%，可见两种选点方案计算结果较为接近。

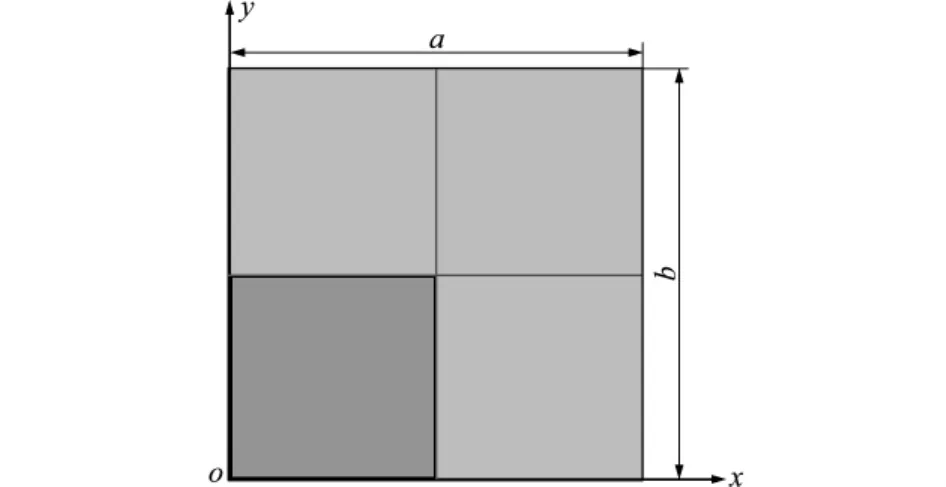
图2 四边简支板Fig.2 Simply-supported rectangular plate

经过20次迭代后，OPT-2过程最大应力迭代变化如图3所示，在第10次迭代得到最优设计结果。两次优化厚度分布如图4所示，可以看出两个优化设计在整体布局上具有相似性。

为了校核优化设计，在给定200s的时间段内，计算初始模型、第一次优化设计（OPT-1）及第二次优化设计（OPT-2）在瞬态传热过程下的位移和应力响应历程。图5给出了传热中间时刻t＝50s时两种优化设计的应力分布，使用相同的标尺对比应力。可以看出，OPT-1设计在温度荷载作用下，存在高应力区域最大Mises应力650MPa；OPT-2设计有效降低了上述区域的应力幅值，最大Mises应力降为282.5MPa。

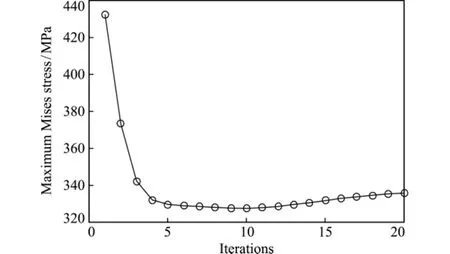
图3 Mises应力最大值迭代历程（OPT-2）Fig.3 Maximum Mises stress via iterations（OPT-2）

图4 优化后厚度分布（单位：m）Fig.4 Optimized thickness distribution（unit：m）

在考虑的时间段内，结构中心位置的z向挠度w如图6所示，等效应力最大值如图7所示。从图6可以看出，在考虑的时间段内，四边简支板中心位置挠度w随时间发生变化，相对于原始均匀厚度模型中心位置挠度值44.1mm，OPT-1和 OPT-2设计都具有较小的中心挠度w，分别为10.49mm和13.81mm。从图7可以看出，在所考虑的200s时间段内，最大Mises应力同样呈较强的随时间变化特性，原始均匀厚度模型的Mises应力最大值为535MPa，由于均匀厚度，其变化相对平缓，OPT-1对应的 Mises应力最大值为683MPa，OPT-2对应的 Mises应力最大值为330.4MPa，可见OPT-2相较于OPT-1，200s瞬态传热过程中的热应力幅值最大值下降了51.6%。

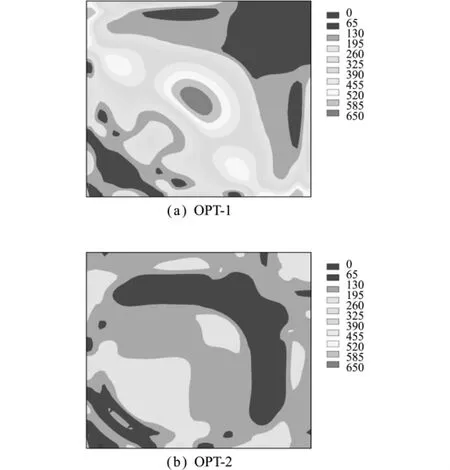
图5 t＝50s时Mises应力（单位：MPa）Fig.5 Mises stress at time t＝50s（unit：MPa）

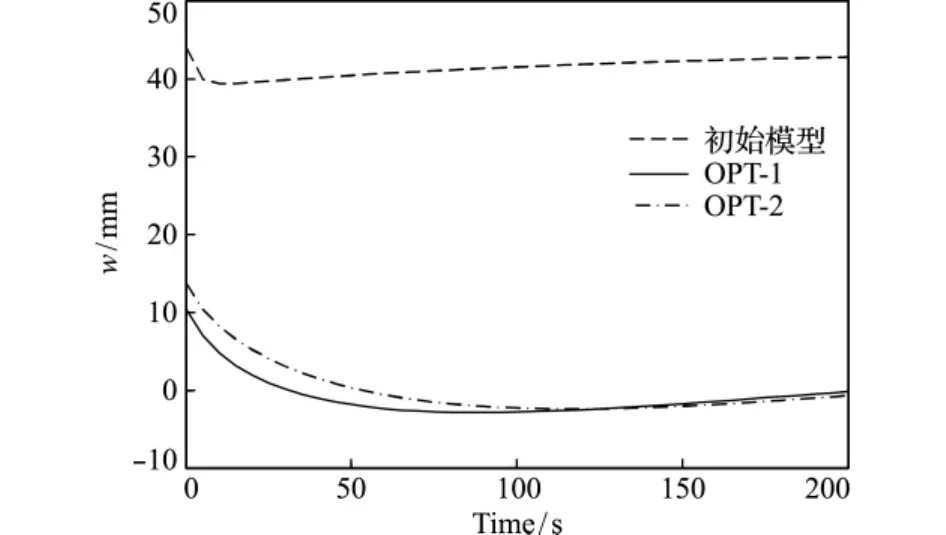
图6 不同时刻中心位置挠度wFig.6 Deflection of center position wvia time

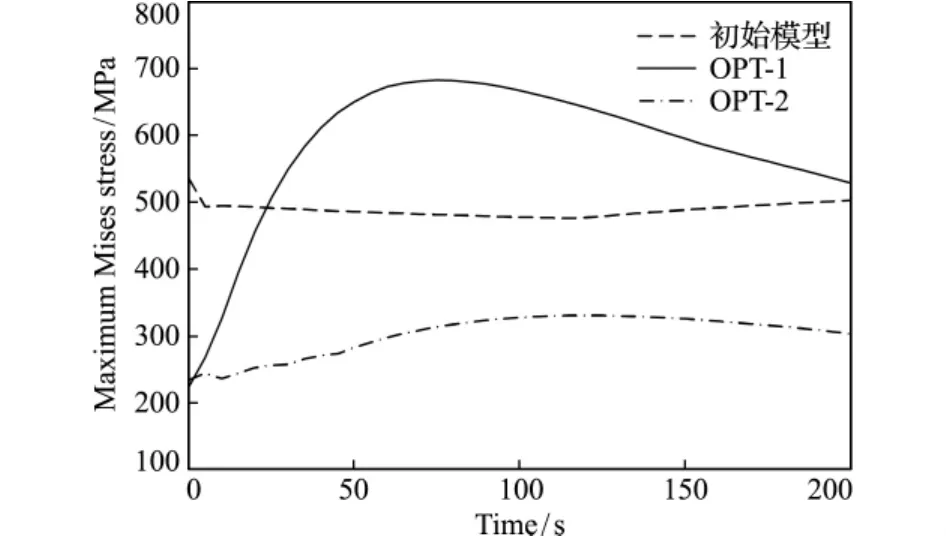
图7 不同时刻Mises应力最大值Fig.7 Maximum Mises stress via time

4 结 论

针对瞬态传热过程中存在的温度场不均衡以及局部应力水平较高问题，采用包络-准则优化方法进行处理。第一次优化设计（OPT-1）使横向位移得到控制，但是应力水平增高较大；经第二次优化设计（OPT-2），相对于第一次优化，位移增量相对较小，而应力水平得到有效降低。经采用的包络-准则优化方法优化后，在控制挠度的同时，也使得结构局部较高的应力水平明显降低，结构刚度和强度特性都得到明显改善，显示了处理此类问题的有效性。