坑中坑式内撑支护基坑围护结构变形特性研究

陈秋旺

(福建西海岸建筑设计院 福建福州 350011)

0 引言

经济的飞速发展，推动了城市地下空间建设。为改善用地紧张缓解交通堵塞改善民生条件等问题，基坑工程不可避免地需要往大深方向发展。与此同时，建筑物或构筑物迎来了多功能性需求，比如需要在基坑内部设置电梯井或集水井，或者因周边建筑裙楼高度不一导致基坑开挖深度各异等，形成了二级基坑开挖，将此类基坑称之为“坑中坑式基坑”(以下简称坑中坑)。

针对坑中坑设计，岩土工程师们往往采取保守设计，在内坑设置较深且刚度较大的地下围护结构，这就造成了一定的材料浪费。即便如此，当二级基坑(以下简称内坑)近邻一级基坑(以下简称外坑)时，坑中坑整体稳定性又难以保证，因此工程设计与施工大多根据现场经验进行判断，关于坑中坑理论设计远远滞后于工程实践。如何准确分析内坑对坑中坑式基坑变形的影响，是目前基坑工程的研究热点与难点。

国内学者龚晓南[1-2]一度认为，应该重视坑中坑式基坑施工安全，设计过程不可忽略内坑对外坑的影响。吴铭炳等[3]依托某实际工程，对坑中坑围护结构变形与土压力进行了现场监测，并结合设计经验，提出了坑中坑支护设计计算深度建议值。陈畅等[4]根据多年的工程经验，认为内坑存在是坑中坑设计的重点与难点，而承压含水层土压力分布与附近堆载等是影响坑中坑变形的主要因素。徐为民等[5]研究了土钉支护坑中坑的滑塌原因，并据此提出了相关设计方法，认为外坑支护体系对内坑支护体系影响微弱。丰土根等[6]以内撑支护基坑为例，分别探讨了内坑相对尺寸与位置对内外坑围护结构侧移的影响，指出设置内坑支撑对控制外坑围护结构的变形有显著作用。

本研究以实际工程为研究背景，通过有限元数值软件Optum G2，建立了可以分析内坑影响的坑中坑数值模型，对坑中坑围护结构的变形特性进行较为系统的研究，同时展开参数分析。相关成果可为坑中坑式基坑设计提供理论参考借鉴。

1 工程概况

某大型公共建筑物占地面积约31 511m2，总建筑面积达28 242m2。该建筑物拥有椭圆形外观，且周边分布裙楼。因主建筑物基坑深度较大，而裙楼基坑深度较浅，基坑系统需要进行二级开挖，构成了典型的坑中坑式基坑，如图1所示。

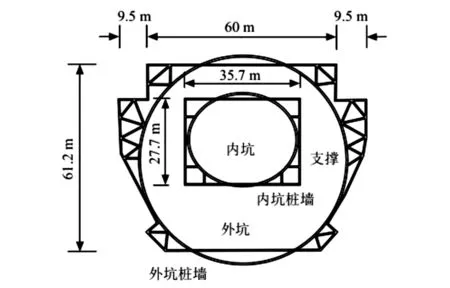
图1 某大型公共建筑物工程平面示意图

假设坑外地表标高为0.0m(GL 0.0m)，不考虑基坑周边荷载影响。基于平面应变条件，取横向基坑建立几何模型，外坑开挖宽度D与深度H分别为60.0m与6.0m。内外坑围护结构为沉管灌注桩，其结构示意图如图2所示。

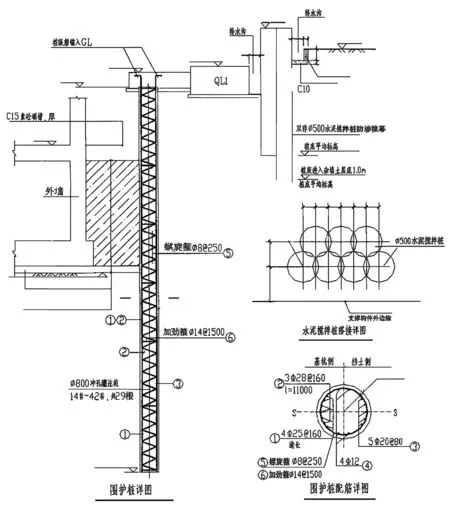
图2 围护桩结构示意图

外坑管桩相对外坑坑底嵌入深度L为6.5m，则围护结构底标高为GL-12.5m，外坑管桩桩径为600@1000mm。在离地表距离为2.0m处，对外坑设置一道水平支撑。取外坑平台宽度即内外坑围护结构间距W为18.0m，内坑开挖宽度d与深度h分别为35.7m与5.5m，对应内坑坑底标高为GL-11.5m，内坑管桩相对内坑坑底嵌入深度l为5m，对应围护结构底端标高为-16.5m，内坑管桩尺寸600@1000mm；在离地表-7.0m深度处(GL-7.0m)，对内坑也设置一道水平支撑，因此，可得到相应的几何模型，如图3所示。

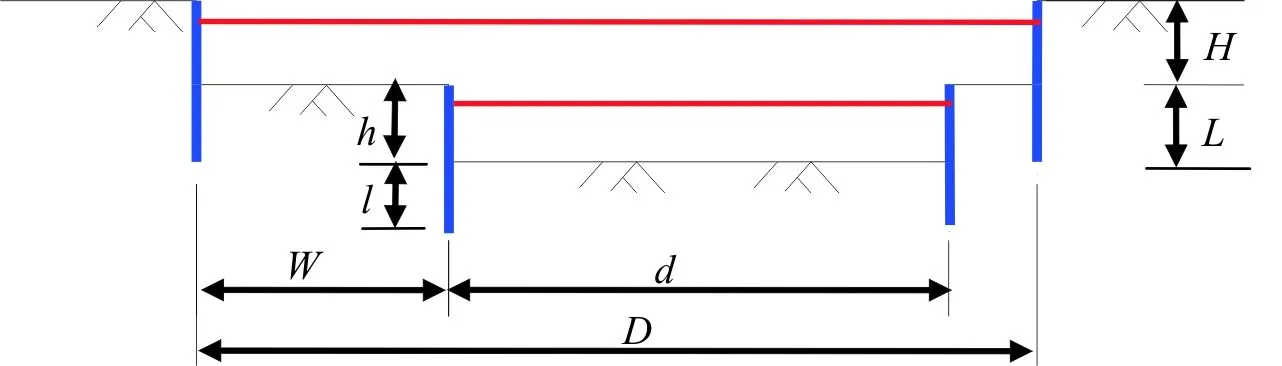
图3 坑中坑式内撑支护基坑几何模型

2 数值模拟及参数选取

利用具有强收敛性与网格自适应算法的二维数值模拟软件Optum G2，采用可以考虑土体加/卸载特性的硬化摩尔库伦本构模型(Hardening Mohr-Coulomb，简称HMC模型)。HMC模型在MC模型的基础上引入土体硬化特征，且同时具备功能参数少且易获取等特点。

该坑中坑施工周期长，且基坑开挖前已完成降水疏干，因此，研究过程理应关注坑中坑长期性能，采用有效应力参数，默认地基土为排水条件。

为更加准确模拟墙-土界面相互作用关系，Optum G2引入了Mohr-Coulomb屈服准则描述墙-土界面摩阻力的发挥及弹-塑性变形特性；定义墙-土界面折减系数为Rinter，界面强度可采用围护结构周边土体强度参数与Rinter的乘积获得：

Rinter=τi/τf

(1)

其中，τi为地基排水条件下墙-土界面的折减强度，τf则为围护结构周边的土体抗剪强度。

参照地勘报告，对建筑物附近地基土土层等厚处理，将相邻近似土层进行整合归并，实现简化分析。为充分考虑基坑开挖影响深度，选择下列代表性土层进行建模计算，表1给出了各土层厚度及物理力学参数。因此，可取数值模型尺寸为180m×67.4m，并采用标准边界条件。数值计算模型如图4所示。

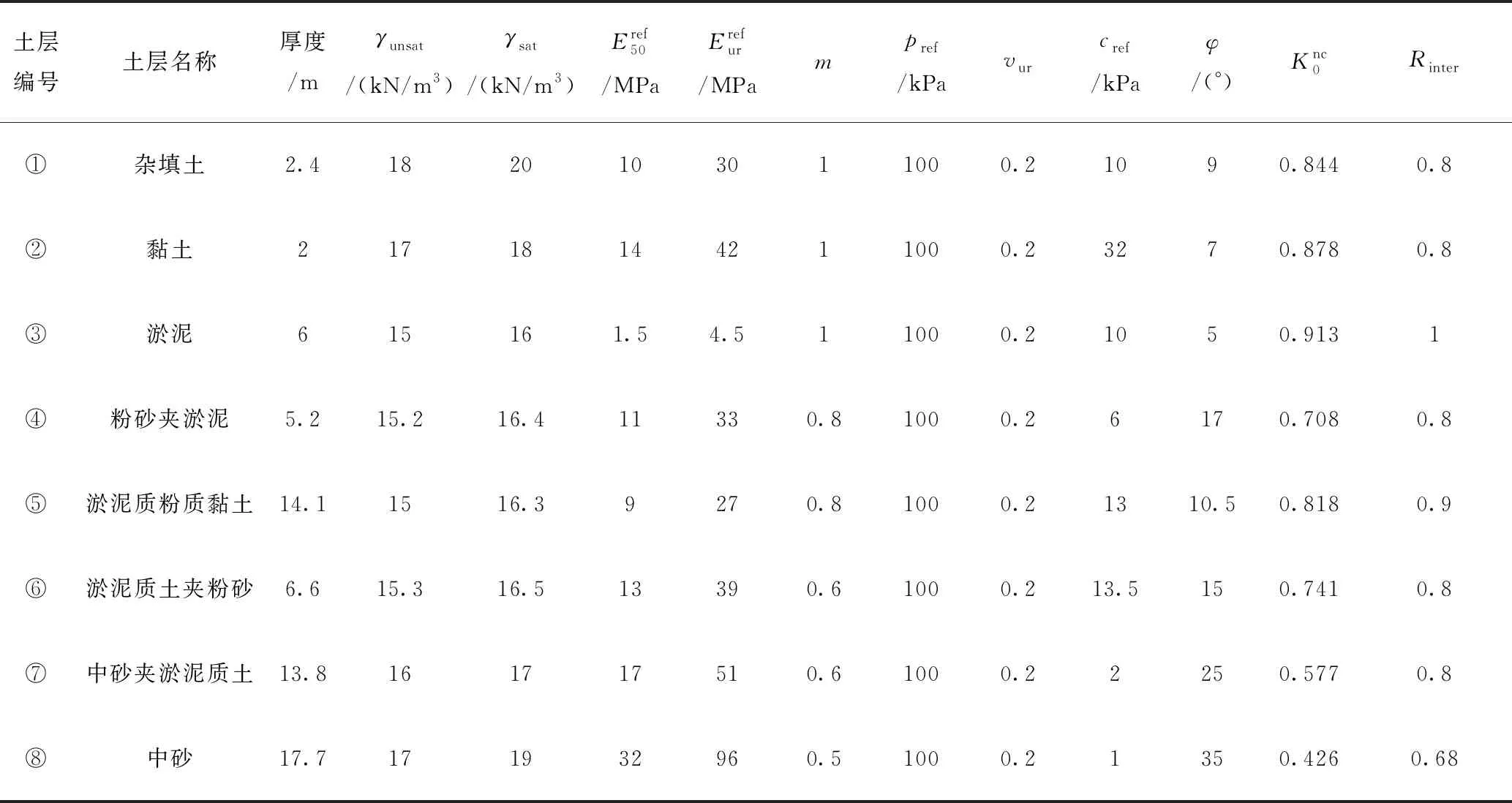
表1 土层厚度及物理力学参数

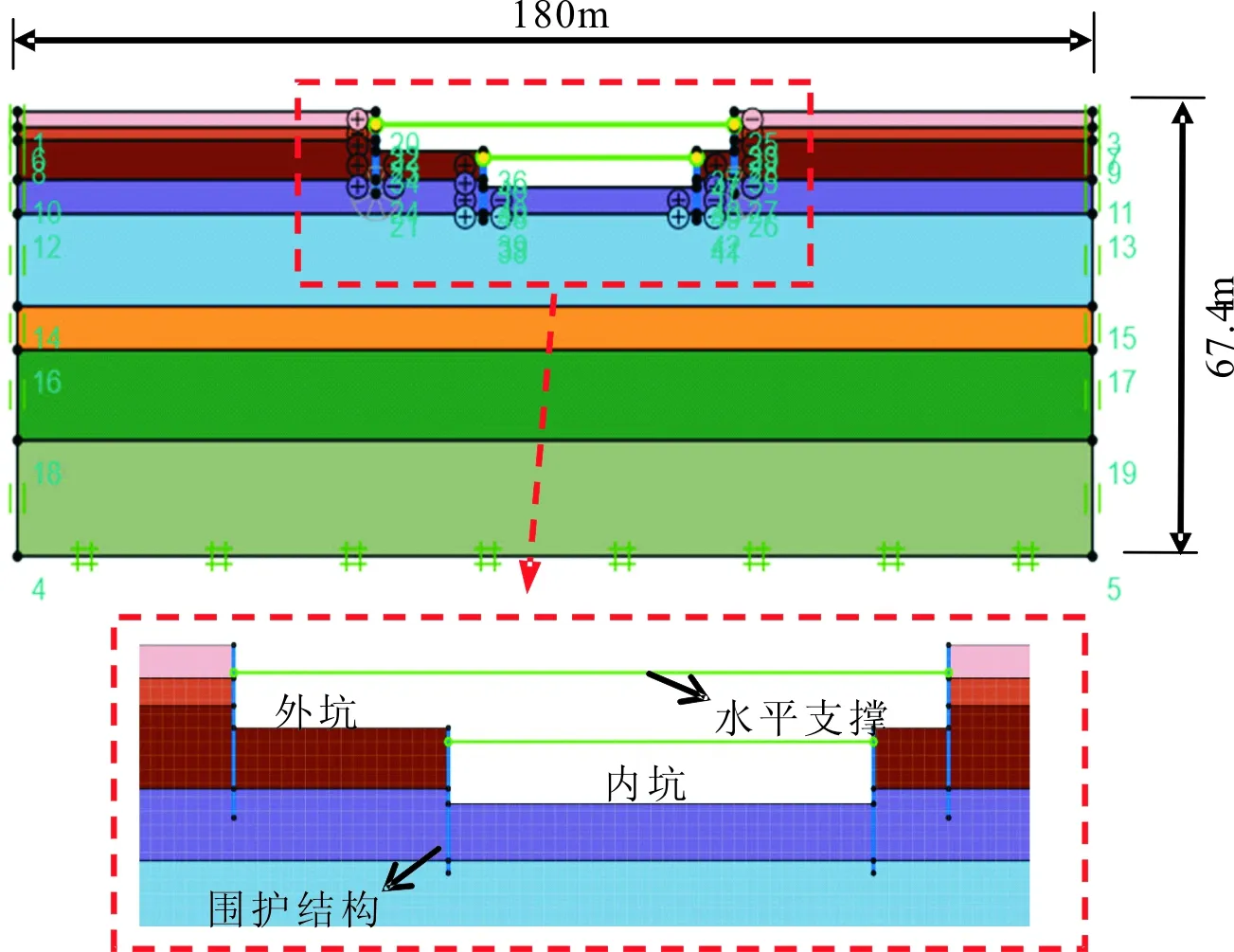
图4 数值计算模型

为便于建模与分析，根据等效刚度法，将离散的管桩结构等效为地下连续墙，显然，其厚度将发生变化。表2给出了转换计算得到的坑中坑支护体系力学参数，相应的计算公式[7]如下：

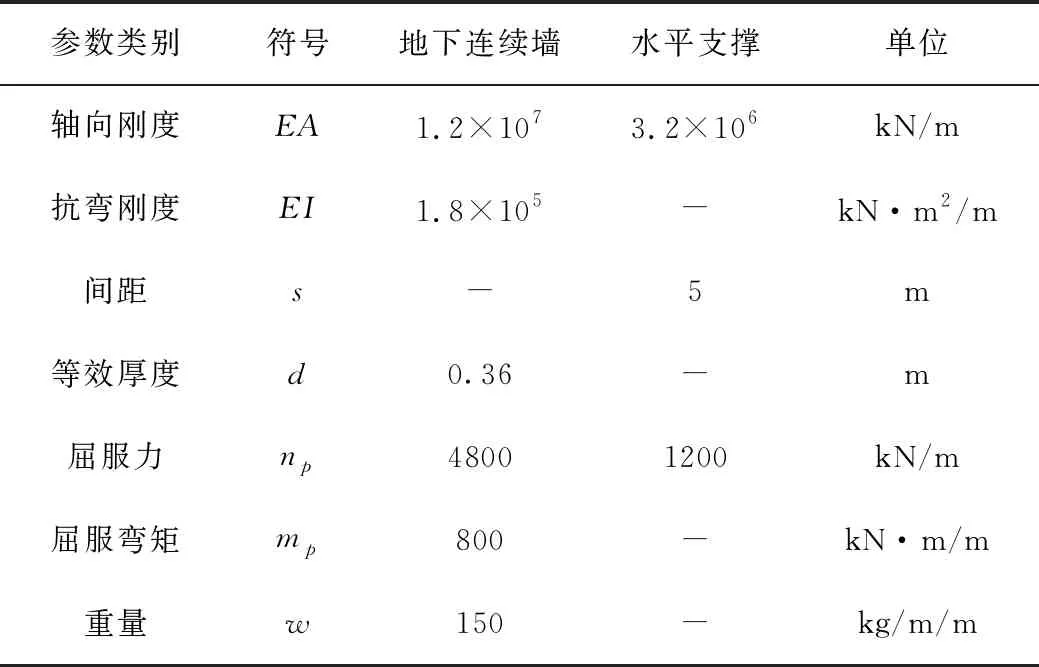
表2 围护结构与水平支撑计算参数

(2)

其中，b为相邻桩中心距；

h等效连续墙厚度；

d为灌注桩桩径。

根据几何模型(图3)与计算参数(表1～表2)建立数值模型如图4所示。采用分步开挖基坑，施工步骤如下所示：

①初始地应力计算；

②浇筑围护结构体系，对应数值模型中激活外坑地下连续墙与内坑地下连续墙；

③开挖外坑第一层至GL-2.5m；

④在外坑GL-2.0m处的设置一道水平支撑；

⑤开挖外坑坑底至GL-6.0m；

⑥开挖内坑第一层至GL-7.5m；

⑦在内坑GL-7.0m处设置一道水平支撑；

⑧开挖内坑坑底至GL-11.5m。

3 对比分析

为充分描述内坑开挖对坑中坑围护结构变形特性的影响，分析过程定义围护结构最大侧移增长率为:

ξ=(δ-δ0)/δ0×100%

(3)

式中，δ0为内坑未开挖，而地基开挖至外坑坑底时外坑地下连续墙最大侧移值；

δ为坑中坑开挖结束时外坑地下连续墙的最大侧移值。

取基坑左侧地下连续墙位移为研究对象，经弹塑性变形分析得到坑中坑开挖结束时外坑地下连续墙的最大侧移值δ为35.30mm，而实测值为32.10mm，计算误差为9.97%，如图5所示；计算得到内坑围护结构最大侧移值为11.27mm，实测内坑最大侧移值12.36mm(图6)，误差为10.09%，误差控制在10%左右，可认为数值计算结果与实测值吻合良好，误差控制在合理范围内，同时证明了采用HMC本构模型可以较为准确合理地反映土体卸荷引起的坑中坑围护结构变形规律。

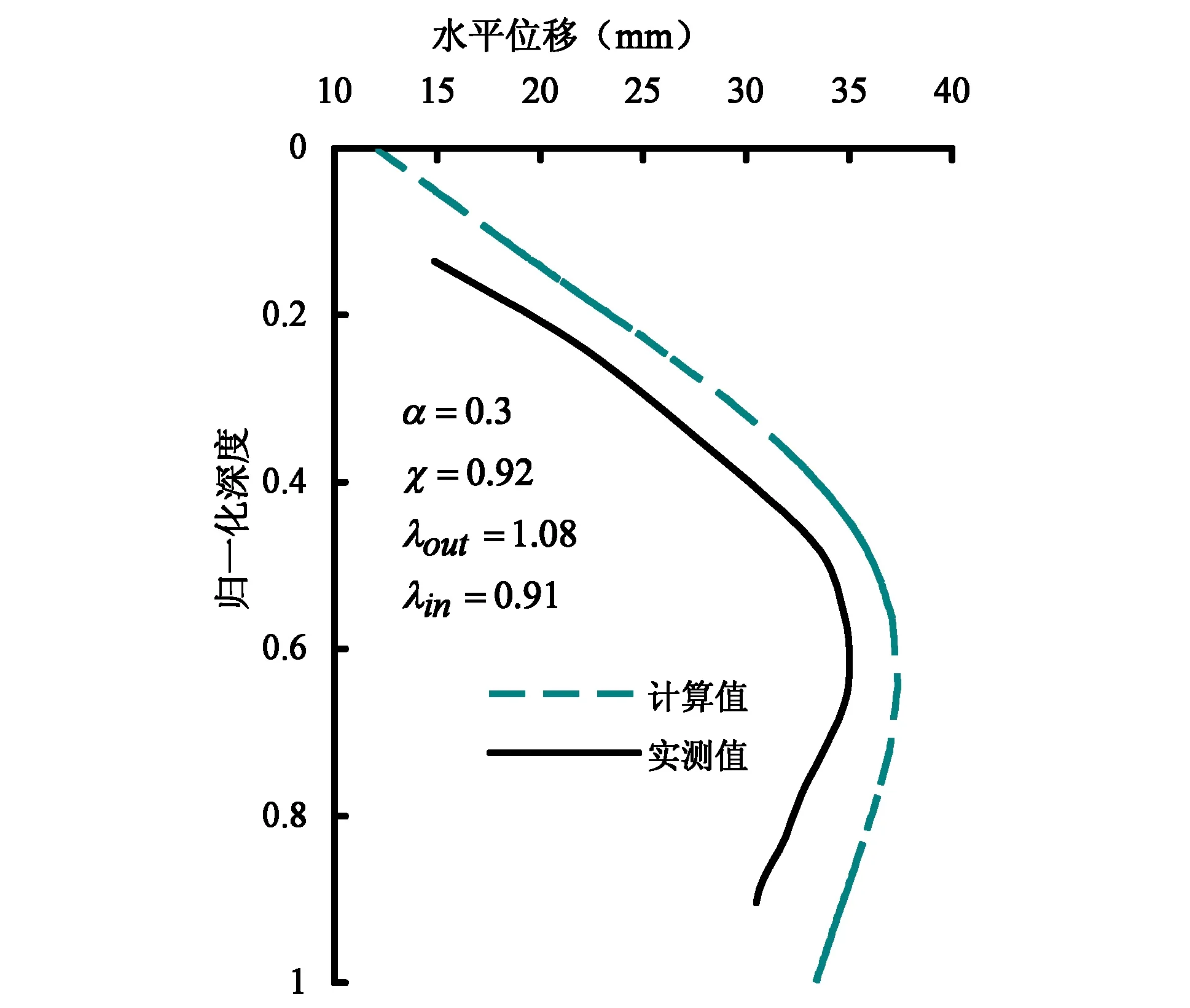
图5 基坑开挖完毕后外坑围护结构水平位移

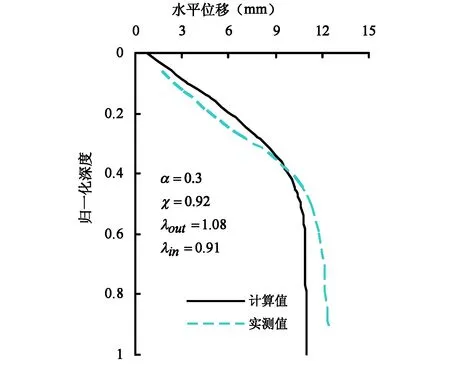
图6 基坑开挖完毕后内坑围护结构水平位移

另外，计算得到地基开挖至外坑坑底时，外坑地下连续墙最大侧移值δ0为29.8mm，围护结构最大侧移增长为18.45%。这说明了一定尺寸的坑中坑开挖，对外坑围护结构的侧移有显著影响。因此，坑中坑设计，考虑内坑的影响十分必要，施工过程应采取合理措施加固坑中坑式基坑，从而降低内坑对基坑的影响，提高整体稳定性，避免安全隐患。

4 敏感性因素分析

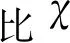
4.1 坑距比

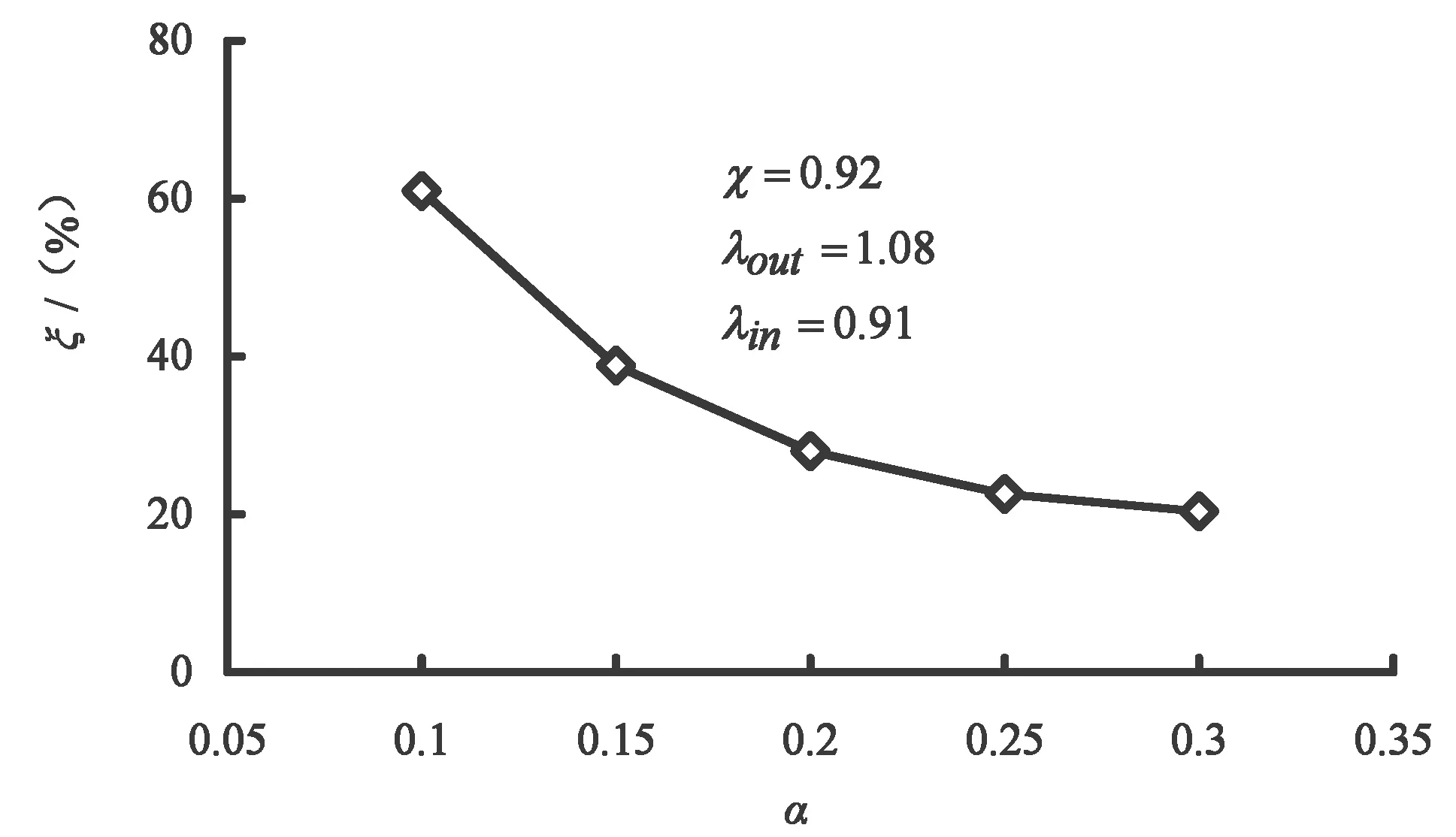
图7 坑距比对外坑围护结构最大侧移增长百分比的影响

4.2 内外坑深度比

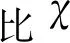
图8 内外坑深度比对外坑围护结构最大侧移增长百分比的影响

4.3 外坑围护结构插入比

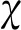
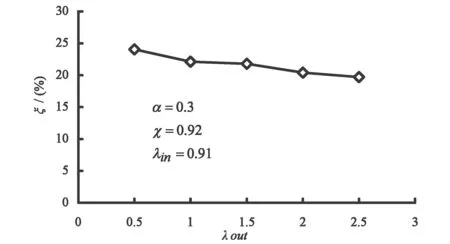
图9 外坑插入比对外坑围护结构最大侧移增长百分比的影响

图10给出了具体原因。分别取不同外坑围护结构插入比下内外坑开挖完毕引起的外坑围护结构侧移最大侧移值δ与δ0的影响。观察图10可以发现，外坑插入深度的增加，最大侧移值δ与δ0几乎呈同步减少，且减少幅度亦十分接近。在两者同步减少情况下，ξ显然变化不大。应该注意，尽管λout对ξ影响较小，但并不意味着设计过程可以忽略该参数。由图8可知，当λout=0.5时，ξ约为25%，可以说对基坑变形有较大影响。当λout从0.5增加至2.5时，δ与δ0均小了大概10mm，因此，适当增大外坑围护结构的插入深度，可以有效控制围护结构的变形并提高基坑的稳定性。

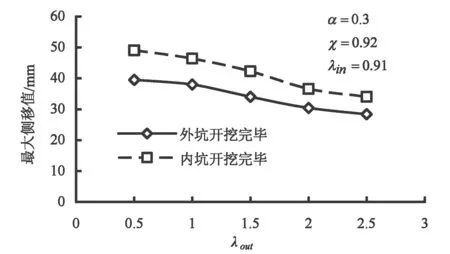
图10 外坑插入比对外坑围护结构最大侧移值的影响

图11 内坑插入比对外坑围护结构最大侧移增长百分比的影响

4.4 内坑围护结构插入比

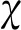
5 结论

(1)采用HMC本构模型模拟地基土，经数值计算得到了坑中坑开挖对基坑围护结构变形的影响，对比内外坑围护结构侧移值与实测值，验证了所建模型的合理性与准确性。通过引入围护结构最大侧移增长百分比ξ，揭示了坑中坑式基坑开挖变形特性，诠释了内外坑相互作用机理，说明了设计与施工考虑坑中坑影响的必要性。

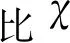
(3)增大λout及λin，将显著降低内外坑围护结构的侧移值，但均对ξ影响不明显。若坑中坑开挖深度有限时，λin取小值，同时适度增大λout，可有效控制基坑变形，并提高基坑整体稳定性能。