甘肃中东部半干旱区参考作物蒸散量多种计算方法的比较研究

黄彩霞,赵德明,王保福

(1.甘肃农业大学水利水电工程学院，甘肃 兰州 730070;2.甘肃省工程咨询中心，甘肃 兰州 730030)

参考作物蒸发蒸腾量(ET0)是区域水资源合理利用和评价、生态系统建模、作物需水量估算的关键因子，对灌溉系统设计、水资源管理具有重要意义[1]。为准确计算不同气候环境下的参考作物蒸散量，国内外进行了大量的研究并提出了基于温度、风速、辐射及综合气象因子计算的多种计算方程[2]，其中，FAO Penman-Monteith方程得到较广泛的认可，通常作为参照与其它方法进行比较，但由于该方程要求较多的气象参数，限制了其在气象资料短缺区的使用。研究表明，一些基于温度或辐射的简单公式在较多地区表现出了广泛的适宜性，同时，不同计算方法间存在显著的线性关系[3]，因此，可根据当地具体的气象条件对ET0进行严格的修正[4-6]。樊军等[7]对黄土区ET0多种计算方法对比表明，Priestley-Taylor计算方法与Penman-Monteith方法结果接近，FAO-Rad， FAO-BC，Hargreaves与Makkink 4种方法与Penman-Monteith方法存在明显的结果和地域差异。李玉霖等[8]对FAO Penman-Monteith、Priestley-Taylor、Makkink、Penman和FAO-24 Blaney-Griddle公式等5种方法进行比较，Penman公式和FAO-24 Blaney-Griddle公式得到的参考作物蒸散量与FAO Penman-Monteith方程结果相近，Priestley-Taylor公式和Makkink公式的计算结果偏差较大，还有研究表明Hargreaves与FAO 56-PM吻合最好[7-8]。

甘肃中东部地区主要分布在黄河干流以东、西秦岭以北地区，占全省面积的1/4左右，属典型的大陆性季风气候，是典型的干旱与半干旱区。该区降水时空分布不均，水土流失严重，干旱频繁发生，特别是随着气候变化和社会经济的发展，干旱的严重程度和影响程度将有可能进一步加剧[9]。由于农业生产在这一区域的社会生产中占重要地位，为缓解该区域水资源不足瓶颈制约，已开展了多种雨水资源高效利用技术和项目建设[10]，目前有关集蓄灌溉的利用效率持续提高、管理制度和规划的完善等成为人们广泛关注的问题[11]。因此，评价和确定当地参考作物蒸发蒸腾量及计算方法对进一步建立健全高效的灌溉制度，优化水资源管理，构建高效节水农业具有积极作用。本文利用典型气象站点长系列逐日气象资料，以FAO Penman-Monteith计算方法为参照标准，计算验证多种公式在该区域的适用性。

1 方法与材料

1.1 参考作物腾发量的计算

(1)FAO Penman-Monteith (FPM)公式[12]。是FAO推荐计算ET0的标准方法，根据参考作物蒸散量的新定义：植物高度为0.12 m，冠层阻抗为70 m·s-1，反射率0.23，类似于地表开阔，高度一致，生长旺盛完全覆盖地表而不缺水的草地蒸发与蒸腾量，属综合法范畴。

式中,ET0为参考作物蒸散量(mm·d-1)，Rn为地表净辐射(MJ·m-2·d-1)，es为饱和水汽压(kPa)，ea为实际水汽压(kPa)，T为2 m高度处日平均气温(℃)，U2为2 m高处日风速(m·s-1)，G为土壤热通量(MJ·m-2·d-1)，γ为干湿表常数(kPa·℃-1)，Δ为饱和水汽压曲线斜率(kPa·℃-1)。以下与此公式符号相同者意义也相同。

(2)Pennman (PM)公式[13]，属综合法范畴。

式中,V为10 m高处风速(m·s-1)。

(3)FAO-17 Penman (17PM)公式[14]，属综合法范畴。

式中,Po，P分别为海平面气压与站点地面气压(hPa)。

(4)FAO-24 Radiation (24PM)公式[15]。该方法源于 Makkink 方程,主要根据太阳辐射资料来估算参考蒸散量，属于辐射法范畴。

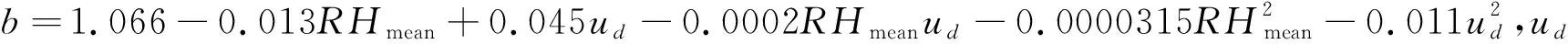
(5)Priestley-Taylor (PT)公式[16]。是 Penman 方程的一种简化形式，属辐射法范畴。

式中,α为常数，取值1.26。

(6)Hargreaves (HA)公式[17]。该方法提出的仅用最高、最低气温计算ET0的简单方法，是典型的温度方法。

ET0=0.0023(Tmean+17.8)(Tmax-Tmin)0.5Ra

(7)Jensen-Haise (JH)公式[18]。属辐射法范畴。

式中,CT为温度系数，λ为蒸发潜热(MJ·kg-1)，Rs为净短波辐射(MJ·m-2·d-1)，T为平均温度(℃) ，Tx为在温度轴上的截距(℃)。

(8)Makkink (MA)公式[19]。属辐射法范畴。

式中,Cr为修正系数，取0.61；Δ为饱和水汽压曲线斜率(kPa℃-1)。

1.2 观测点选择及气象数据来源

本文所选范围介于104°32′～108°42′E和34°05′～37°09′N之间，包括庆阳、平凉、定西、天水4个地区，观测点按照“十”分布，共选取6个气象站点，气象资料来自于中国气象局，其中临洮县(103°51′E，35°21′N，海拔1 894 m)、秦州区(104°45′E，34°35′N，海拔1 142 m)为1951-2013年63 a逐日气象资料；通渭县(105°14′E，35°13′N，1 768 m)，静宁县(105°43′E，35°31′N,海拔1 660 m)、灵台县(107°37′E，35°04′N,海拔960 m)和秦安县(105°40′E，34°52′N,1 054 m)为1960-2013年54 a逐日气象资料，包括平均气温、最高气温、最低气温，水汽压、风速、日照时数、气压等。

1.3 数据分析方法

本文利用Excel和dps统计软件。使用误差分析和线性回归比较计算结果。主要统计变量有平均偏差(MBE)、标准偏差(RMBE)，用公式表示为：

式中,yi为计算值，xi为利用PM公式计算的ET0。

2 结果与分析

2.1 各方程年ET0值计算结果比较及评价

图1是采用不同方程计算的多年ET0均值，不同方程计算的各地区ET0趋势基本一致，但同一地区不同方程间存在明显差异。与FAO Pennman-Monteith比较可以看出(图2，图3)，Hargreaves与FAO Pennman-MonteithET0最接近，各地区平均MBE为-109.2 mm、RMBE为120.0 mm，说明Hargreaves计算的ET0总体偏小，这与刘晓英等[20]对华北地区ET0计算结果一致。Jensen-Haise的计算结果仅次于Hargreaves，各地区平均MBE为-433.2 mm、RMBE为446.1 mm。其它5种方程中Pennman、FAO-17 Penman、FAO-24 Radiation、Preiestley-Taylor计算结果偏高，各地区平均MBE在3 069.9～1 359.9 mm之间、RMBE在3 122.1～1 383.4 mm间，以FAO-24 Radiation相差最大，各地区ET0是FAO Pennman-Monteith方程的2.84～2.59倍；Priestley-Taylor、FAO-17 Penman、Pennman也分别达到1.86～1.68倍，1.46～1.24倍、1.28～1.14倍。Makkink计算结果偏低，差异较大，MBE为-941.0 mm、RMBE为956.3 mm。采用t双侧检验表明，各区域不同方程与FAO Pennman-Monteith方法计算的ET0，回归系数t在298.56～6.85之间，在0.01置信水平上具有显著差异(t0.01=2.68)，因此，在西北干旱区采用其它方程计算ET0年值尚需矫正后方可使用。

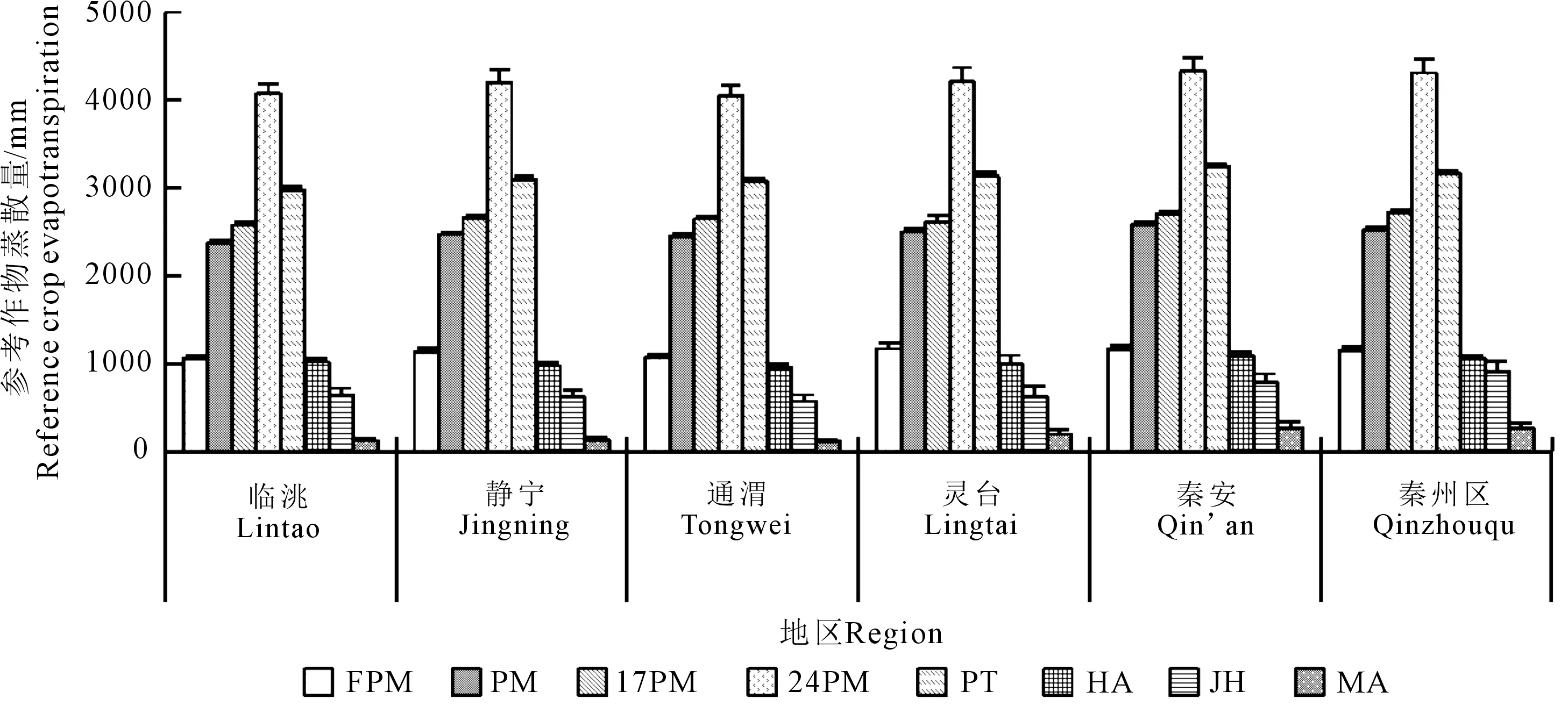
图1 不同方程计算的各地区参考作物蒸散量年均值Fig.1 The average annual ET0 calculated for various districts using different methods

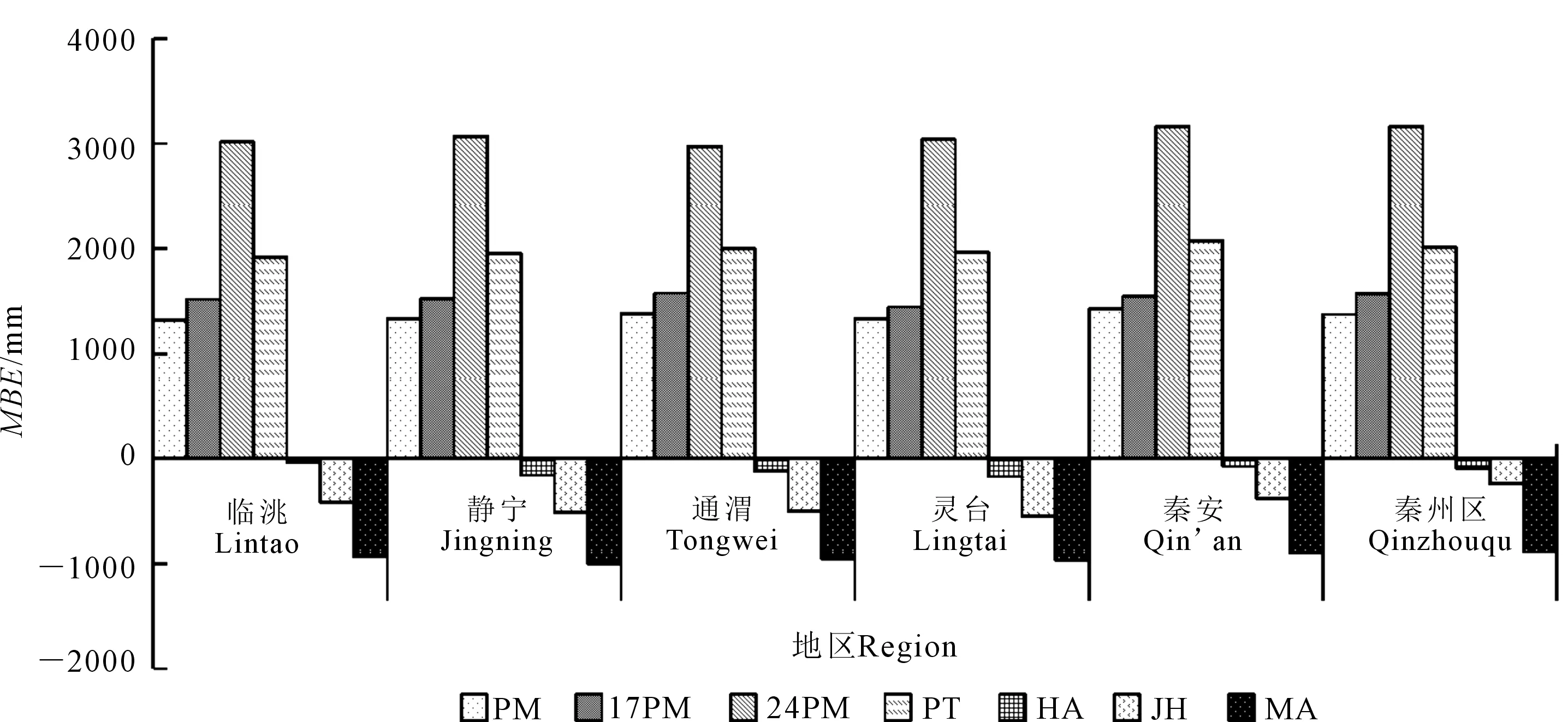
图2 不同方程与FAO Penman-Monteith计算的ET0间的平均偏差Fig.2 The MBE of calculated ET0 values using FAO Penman-Monteith method and other methods

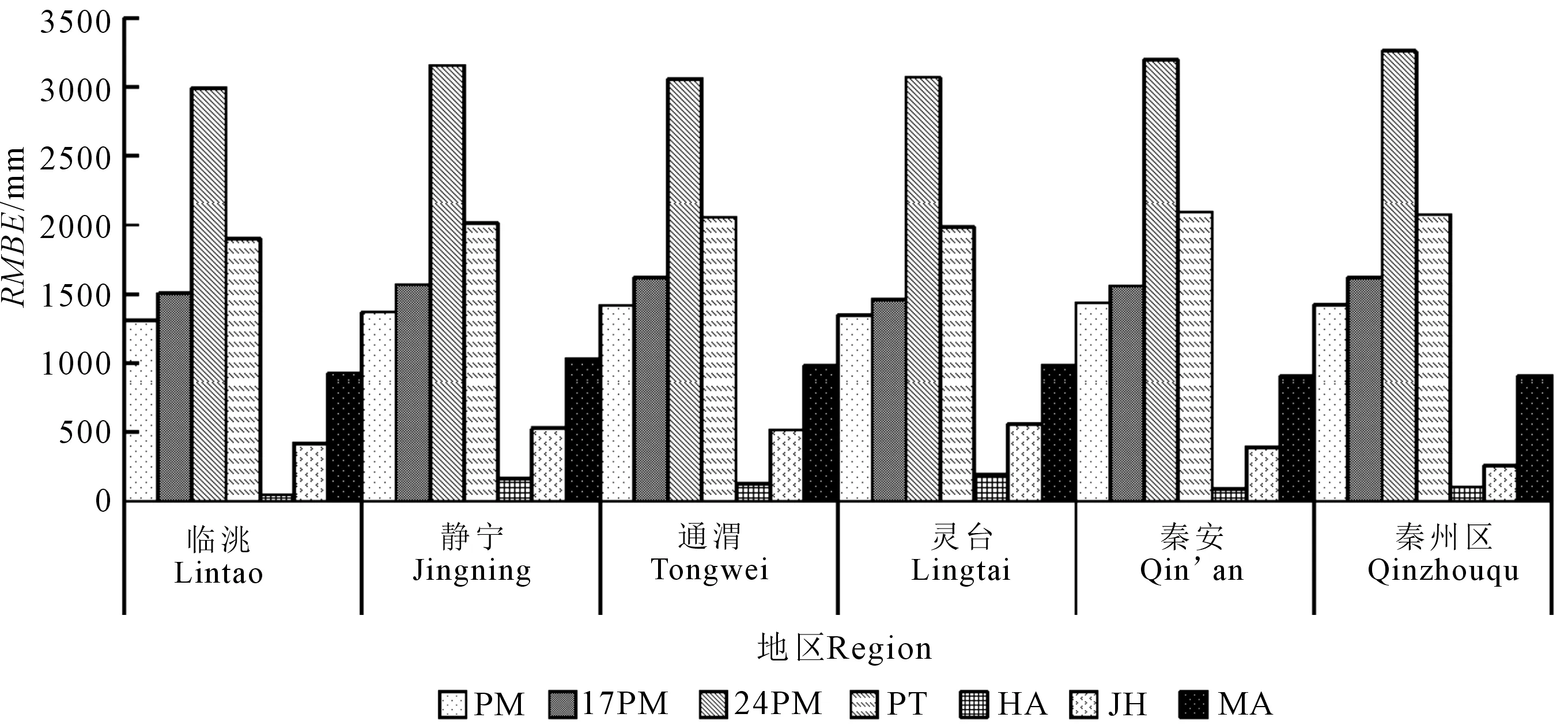
图3 不同方程与FAO Penman-Monteith计算的ET0间的标准偏差Fig.3 The RMBE between FAO Penman-Monteith method and other methods for calculating ET0

以FAO Penman-Monteith方法为自变量，其它方程为因变量进行线性回归表明(表1)。不同的方程与FAO Penman-Monteith方程均存在显著的线性相关关系(0.994**≤R≤0.8743**)。各方程中，Hargreaves方程回归系数(b)在 0.897 1～0.988 4间，与FAO Penman-Monteith拟合性高，回归系数t检测达到显著水平；Pennman、FAO-17 Penman、FAO-24 Radiation、Preiestley-Taylor 4种方程回归系数(b)远大于1， Jensen-Haise和Makkink方程回归系数(b)均小于1，说明不同地区不同方程对ET0的计算同样存在高估或低估的问题。各方程回归系数t检测均达到显著水平，说明与FAO Penman-Monteith方程ET0存在显著的线性关系，对各方程采用回归方程进行矫正是可行的。

2.2 各方程月均ET0值计算结果比较

图4可以看出，6个气象站8种方程计算的月均ET0趋势基本一致，年内ET0呈单峰曲线，峰值出现在7月份。与FAO Pennman-Monteith计算的月ET0值相比，Hargreaves方程计算结果最相近，曲线几乎重合，各地区间年内月均ET0RMBE为12.05 mm，地区差异以临洮最小，年内月均ET0RMBE为6.69 mm，灵台最大，RMBE为18.48 mm，其它地区差异相近，RMBE为14.33～10.59 mm。各地区月份间差异3-9月(各地区平均RMBE为14.02～19.55 mm)高于1-2月(各地区平均RMBE为9.87～6.6 mm)和10-12月(各地区平均RMBE为6.38～5.53 mm)。

Jensen-Haise的计算结果与Penman-Monteith也较接近，各地区间年内月均ET0RMBE为38.99 mm，地区差异以秦州区最小，年内月均ET0RMBE为27.89 mm，灵台最大，RMBE为48.62 mm。各地区月份间最大差异出现在4月份，平均RMBE为53.53 mm，最小值出现在12月份，平均RMBE为22.59 mm。

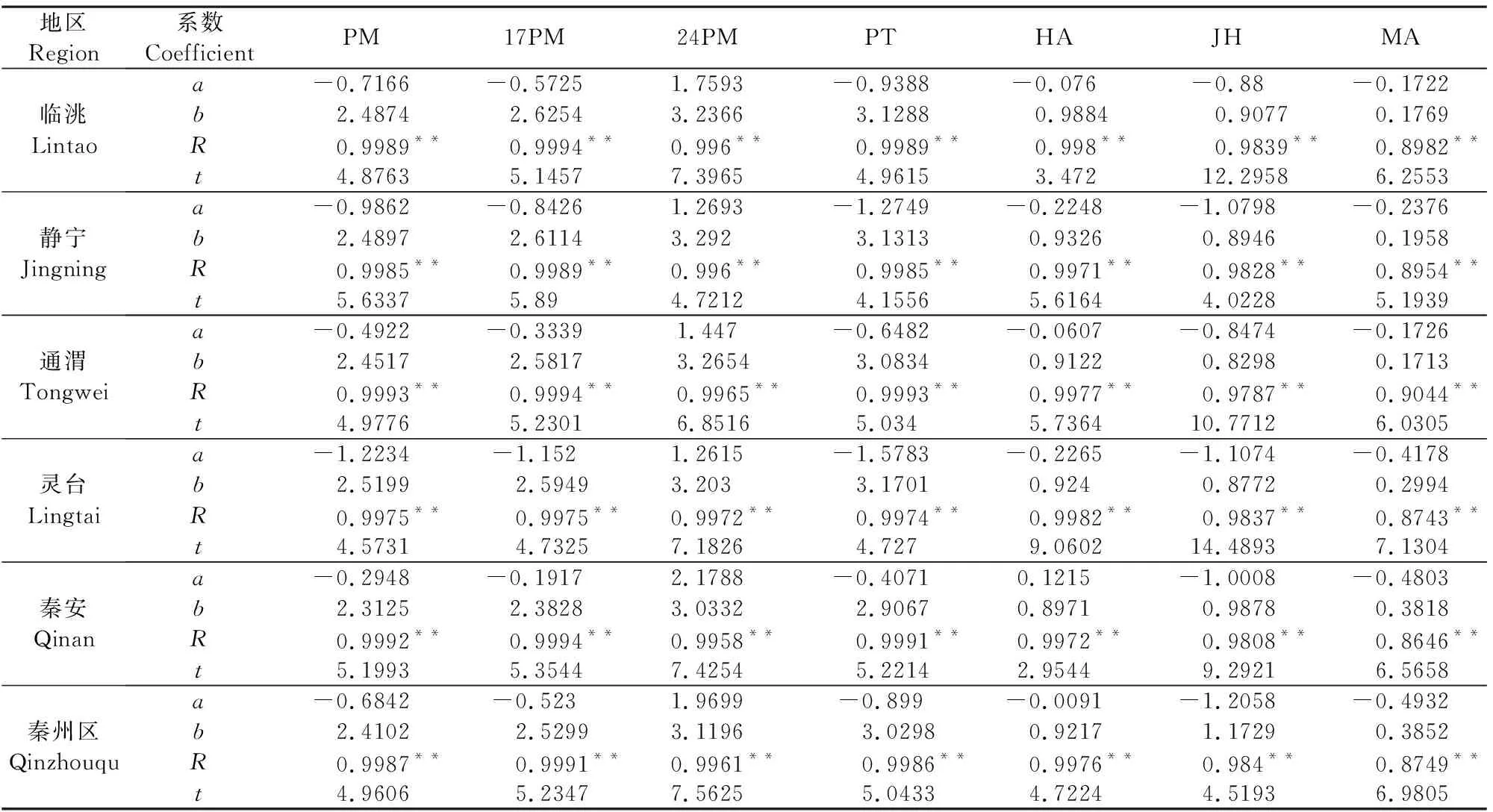
表1 FAO Penman-Monteith与其它方程间的回归系数

注：*表示显著相关，**表示极显著相关。

Note:* indicate significant correlation, ** indicate highly significant correlation.

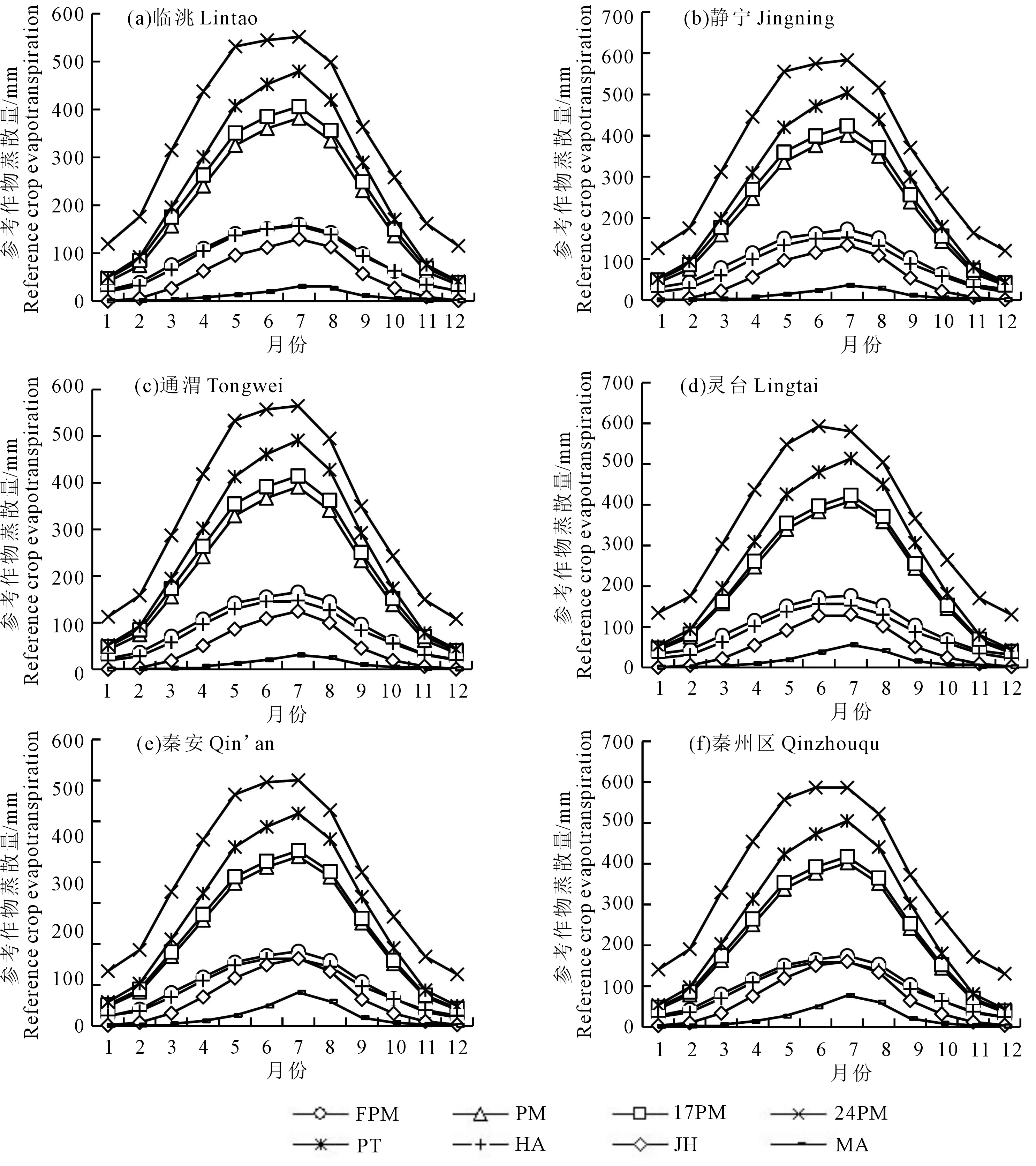
图4 不同方程计算的各地区参考作物蒸散量月均值Fig.4 The average month of ET0 calculating in different districts using different methods

Pennman、FAO-17 Penman、FAO-24 Radiation、Preiestley-Taylor 、Makkink 5 种方程的计算结果都与FAO Penman-Monteith 相差较大且差异程度随着ET0的增大而增大，5种方程RMBE呈单峰曲线，峰值出现在6-7月份，其中，Pennman、FAO-17 Penman、FAO-24 Radiation、Preiestley-Taylor 4种方程计算结果偏高，以FAO-24 Radiation差异最明显，各地区间年内月均ET0RMBE为257.42 mm，其次为Preiestley-Taylor，RMBE为166.56 mm，FAO-17 Penman RMBE为128.48 mm，Pennman RMBE为114.19 mm；Makkink计算结果总体偏小，明显低估了ET0，各地区间年内月均ET0RMBE为79.19 mm。

3 结论与讨论

1)以FAO Penman-Monteith方法为参照标准，对其它方法进行验证表明：在甘肃中东部地区Hargreaves公式计算的ET0值较FAO Penman-Monteith方法更接近，其次为Jensen-Haise公式。说明在缺少辐射和风速资料的地区，Hargreaves和Jensen-Haise公式可以获得较好的计算结果，这与赵璐等[21]对川中丘陵地区研究结果一致，胡庆芳等[22]研究也表明，校正后的 Hargreaves 公式，对于西北地区大部分站点在年内各月均具有较强的适用性。Pennman、FAO-17 Penman、FAO-24 Radiation、Preiestley-Taylor 计算结果差异较大，计算结果偏高，Makkink总体也偏低，这与樊军等[7]研究结果一致，但与李玉霖等[8]、毛飞等[13]研究结果不一，导致不同方程计算偏差的原因是各种方程各自选用了不同的辐射项和动力项计算公式。

2)不同方程与FAO Penman-Monteith方程均存在显著的线性相关关系(R≥0.8743**)，在实际应用中，可以根据气候条件的差异适当调整回归系数，以便准确地估算参考作物腾发量[2,7,23]。

3)不同方程年内ET0呈单峰曲线，峰值出现在7月份，方程间的差异随ET0值的增大而增大。其中，Hargreaves方程各地区月份间差异3-9月(各地区平均RMBE为14.02～19.55 mm)高于1-2月(各地区平均RMBE为9.87～6.6 mm)和10-12月，地区间差异随月份不同而不同，这可能与风速和降雨的影响有关[6,24]，胡庆芳认为， Hargreaves 公式无法有效描述ET0中的空气动力学项是计算误差产生的主要原因[22]。Jensen-Haise方程各地区月份间最大差异出现在4月份，平均RMBE为53.53 mm，最小值出现在12月份，平均RMBE为22.59 mm。左德鹏等对不同气候区基于辐射潜在蒸散量比较表明，Jensen-Haise方程计算误差与气象站点的湿度有关，通常随着湿度的增大误差增大，冬季误差小夏天误差大[25]。Pennman、FAO-17 Penman、FAO-24 Radiation、Preiestley-Taylor 、Makkink 5 种方程的计算结果都与FAO Penman-Monteith 相差较大且随着ET0的增大而增大，主要是因为气象因子对辐射项和空气动力项的不同影响造成，有关太阳辐射数据国内尚存在时间短、地区少、数据质量不高等问题，因此，在选用公式时，还需要根据资料状况做进一步对比分析工作。