超高分子量聚乙烯平纹织物的穿刺冲击模拟与响应分析

邹画眉 刘新金 谢春萍 苏旭中 徐伯俊

摘要： 运用有限元方法对带刃刀具刺穿超高分子量聚乙烯平纹织物的冲击过程进行数值模拟，并通过准静态实验验证有限元模型的有效性。通过给出布面刺破效果的数值仿真模拟，对织物刺穿过程中的纱线的应力应变分布进行分析，得到冲击系统的能量变化规律。数值模拟结果指出：刀刺织物过程中，刀具的能量主要转化为织物的弹性应变能，其余为塑性耗散能和摩擦耗散能;纱线破坏以剪切断裂为主;平纹织物的弹性回复性能有助于抵抗刀具的冲击，增强其抗剪切性能是提高防刺性能的關键。

关键词： 有限元;平纹织物;穿刺;准静态实验;能量

中图分类号： TS101.923   文献标志码： A   文章编号： 1001-7003（2019）06-0046-06    引用页码： 061108

Abstract： The impact process of the edged cutter piercing UHMWPE plain weave fabric was numerically simulated by finite element method， and its effectiveness was verified by the quasi-static experiment. The numerical simulation of cloth surface piercing effect was given to analyze stress and strain distribution of yarns in the piercing process， and the energy change law of impact system was gained. The numerical simulation results show that the energy of the cutter is mainly converted into elastic strain energy of fabric in the fabric piercing process， while the rest is plastic dissipation energy and friction dissipation energy. The failure of yarns is mainly due to shear fracture. The elastic recovery property of plain fabric is helpful to resist the impact of cutter. Enhancing shear resistance of the plain fabric is the key to improve its stab-proof performance.

Key words： finite element; plain weave; puncture; quasi-static experiment; energy

柔性织物和纺织结构复合材料因其质轻柔软、高强耐冲击的特点被广泛运用在特种防护织物，如击剑服、防刺防弹服的研发上[1-2]，其中最典型的代表就是纤维增强复合材料。而纤维增强体在纤维增强复合材料中提供材料的强度和刚度，起主要作用[3-4]，因此，对于增强体的力学研究和抗冲击性能预测颇为重要。利用有限元模拟计算纤维增强体在冲击下的力学响应，一方面避免了制作大量的试样，降低了生产成本;另一方面能够更细致深入地分析纺织结构的力学响应，这是单纯进行力学实验所不能达到的，因而成为了当下的研究热点。

有限元分析包括建模、材料属性赋予、建立分析步、设置相互作用、划分网格、施加载荷与边界条件、提交任务与可视化分析等步骤[5]。本文利用有限元软件Abaqus模拟分析了带刃刀具穿刺平纹织物的静态力学响应与动态力学响应，探寻穿刺的基本机制，以期对平纹织物防刺性能的提高提出建设性的思路。刀具穿刺织物过程含有大变形和复杂的接触关系，是高度非线性问题，采用隐式动力学（Standard）分析很难收敛，因此用显示动力学方法（Explicit）进行分析。实际生活中，人持刀具穿刺织物过程中，刀具的速度不仅受织物的反作用，还受变化的外力或重力操控，但是在使用计算机进行动态穿刺模拟时，忽略人力，给刀具一个初始速度，只考虑织物与刀具间的相互作用，简化研究过程，探寻冲击响应基本规律，为防刺材料的复合结构设计与力学性能预测奠定理论基础。

1 冲击系统建模与前处理

整个穿刺冲击系统包括织物与刀具两部分。平纹组织是最基本的二维机织物结构，因为它在二维机织物中最为紧密坚牢，所以应用最为广泛。超高分子量聚乙烯（Ultra-high molecular weight polyethylene， UHMWPE）是目前抗冲击性能最高[6]的高性能材料之一，因此，本文选用一种超高分子量聚乙烯平纹织物材料进行仿真模拟，刀具选用参考GA 68—2008《警用防刺服》。

UHMWPE纤维的力学性能具有应变率敏感性，即在不同的应变速率下，其应力应变曲线不同。特别在高应变率（102～104s-1）与超高应变率（104～106s-1）下，UHMWPE材料会有明显的模量增加、最大应力增大与失效应变减小现象。而本文所研究的刀具穿刺织物过程为低速冲击，属于中应变率实验。如GA68—2008《警用防刺服》中对防刺性能测试的规定：让质量为2.4kg的刀具自由落体以（24±0.5）J的撞击能量刺入织物并检查织物能否穿透。经计算，标准中刀具接触织物时的速度约为4.47m/s，而实际生活中，手持刀具穿刺织物的速度不超过10m/s，穿刺过程中纤维纱线的应变率小于102s-1，纤维纱线的力学性能与静态等速拉伸试验（应变率约为10-2s-1）时的力学性能差异不明显。且本文的动态穿刺模拟只作为探讨穿刺机制的研究手段，不作为实际材料防刺性能预测的依据。因此，有限元模型中暂且忽略了UHMWPE的应变率效应，假设纱线在动态穿刺过程中的应力应变曲线与静态拉伸实验所测得的参数一致。

1.1 建 模

1.1.1 织 物

平纹织物试样的组织结构参数通过超景深三维显微镜拍照测量取得，如表1所示。用各种CAD软件建模再将模型导入有限元软件，存在计算速度慢与信息易丢失的缺点，因此，建模操作在有限元软件Abaqus自身的Sketch模块进行，按照实际织物试样的结构参数1 ︰ 1画出纱线，建立8cm×8cm大小的织物模型。因实际织物中纱线相互交织，交织点处纱线相互压扁，因此假设纱线截面为椭圆形，这样亦不易造成纱线间的过盈接触。将椭圆截面沿着样条曲线扫掠便可得到一根纱线的模型。将一根纱线通过阵列和三维旋转等操作，画出平纹织物的模型（图1）。

1.1.2 刀 具

不同刀具的穿刺机制不同[7]。美国NIJ 0115.00《个体防刺衣》标准中，将刀具分为有刃刀具和锥形刀具，有刃刀具又分为单侧刃和双侧刃刀具。锥形刀具冲击织物过程中不含有剪切作用，只有拉伸断裂破坏;一般刀具都为带刃刀具，穿刺织物的过程中既有剪切破坏，又有拉伸破坏。中国公安部GA68—2008《警用防刺服》标准中的规定实验刀具即为一种单侧带刃刀具，具有典型代表性。

按照GA68—2008《警用防刺服》中标准刀具的参数绘制刀具模型。考虑到刀具刚度非常大，穿刺过程中几乎不会形变，也无需考察其应力分布，因而将刀具定义为离散刚体，不需赋予材料属性，只需定义参考点。为了减少单元数量、加快计算速度，只画出其刀尖部分。

1.2 前处理

1.2.1 赋予材料属性

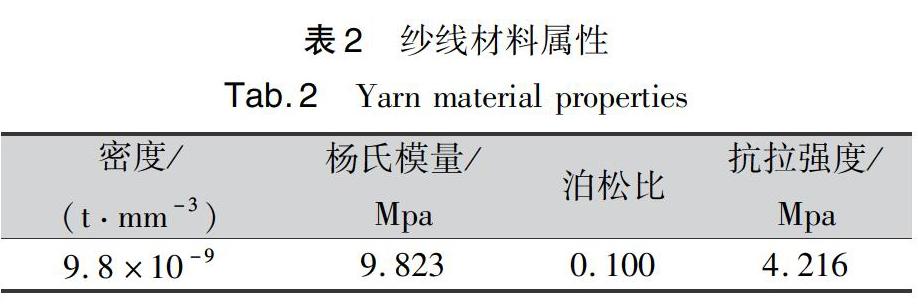
本文模拟的二维织物选用高性能纤维——超高分子量聚乙烯（UHMWPE）作为材料，拆取试样织物的多根UHMWPE纱线进行拉伸断裂等实验，得到纱线的弹塑性等属性参数如表2所示。在Property模块中输入属性参数，定义失效准则，并设置与位移相关的损伤演化。

1.2.2 划分网格

用刚性单元划分离散刚体，刀具共划分为了2093个R3D4单元;用减缩积分单元划分实体，纱线共划为17600个C3D8R单元，同时增加一个人工的沙漏刚度以防止出现沙漏现象。

1.2.3 其他前处理

将刀具与织物装配好（图2），刀尖与织物表面接触，首先给刀具的参考点施加一个10000mm/s的恒定速度约束，给织物四周的纱线端施加PINNED约束（位移为0），纱线间、纱线与刀具间的摩擦系数设为0.1，建立显示动态分析步，提交计算任务，得到静态穿刺数值模拟结果。

2 准静态实验验证

2.1 实验过程

利用万能试验机对UHMWPE平纹织物试样进行准静态刺破实验（图3），刺破过程尽量均匀缓慢，以保证各时刻冲击系统的状态接近平衡态。用自制的正方形夹具夹住布样，实验前将刀头下降到与布样表面刚好接触，布样有效受力范围为8mm×8mm，设置实验过程中刀具下降速度为10mm/min后开始实验。

需要说明的是，在Abaqus软件中用显示动力学方法（Explicit）模拟准静态问题时，稳定时间增量很小，以自然周期（10mm/min×1.3min）计算将耗费相当长的时间，是不切实际的。因而为提高计算效率，需要人为地提高刀具设定速度，将时间长度控制在0.01s以下。在有限元中尝试了2000～12000mm/s的不同刀具速度设置，发现：速度为2000～6000mm/s时，计算效率很低;速度大于11000mm/s时，伪应变能很大，织物动能/内能的比值过大，计算中断，结果失真;速度为7000～10000mm/s时，计算效率较高，且不同速度的数值模拟结果具有一致性，具有参考价值。因此，将有限元中刀具速度设置为10000mm/s。

2.2 实验结果

将Abaqus数值模拟结果与刺破实验结果相比较，可以发现：两者冲击后的布面形态高度相似，纱线转曲滑移的位置形态及破口的大小基本一致（图4），实验布样的破口略小，可能是由实验结束后刀具抽出布样稍有回复导致的。对比两者刀具的顶破力-位移曲线（图5）亦可发现一致性。两条曲线的走向基本吻合，在7mm和11mm左右均有明显的顶破力下降和震荡，分析认为是由于纱线的失效断裂导致，而模拟的结果比实验结果略有延迟，但亦在误差允许范围内。由此可以验证：织物的建模方式有效，有限元中纱线的属性参数设置相对准确，刀具速度的数量级提高没有使结果退化失真，在可接受的范围内。

3 冲击响应分析

为探寻布面受到刀具冲击后响应的基本规律，决定给刀具一个初始速度，只考虑织物与刀具间的相互作用，不考虑外力做功，从而简化研究过程。在Abaqus软件中可以实现这种理想状态。实际織物织制得非常紧密，且纱线无捻，导致纱线扁平，宽高比很大，截面某些地方曲率过高，不利于网格的划分。因此在Abaqus中用同样的建模方式建立一个经纬密较小、纱线更圆的织物模型，纱线属性设置及其他前处理方式与上文相同。假定刀具与织物接触时的速度为8m/s，设置模型中刀具的初始速度为8000mm/s，提交计算任务，分析动态穿刺数值模拟的结果。

3.1 刺穿过程

图6显示了刀具刺穿织物而后被弹回的过程中织物的应力变化与变形情况。由此动态云图可以看到：0～0.0045s，刀具渐渐刺入织物，纱线受到挤压拉伸，布面渐渐突起;0.0045s时，织物凸起最为明显，纱线开始断裂;到0.005s刀具刺穿平纹织物、其中一根纱线完全断裂后，织物显现出一个收紧的趋势，刀具不再刺深并向相反方向移动;直到0.0075s时，织物继续收紧回复，刀具又后退了一些距离。结合刀具的速度曲线、位移曲线（图7），可以总结出整个刺穿过程分为刀具刺入与被弹回两个阶段。

3.2 织物的应力应变分布

从图6中的应力分布可以看出，刀尖从纱线空隙中刺入，纱线受到挤压拉伸，应力逐渐提高。主要体现在随着刀具的深入，与刀具接触部分纱线变形增加，应力持续增大，纱线与纱线交织点处的应力也逐渐增加，同时，织物四周的固定端出现应力集中。而刀尖四周部分纱线应力最大，这是因为此处所受的拉伸力与剪切力最大。通过查询节点力值，发现纱线断裂前的拉伸应力远未达到抗拉强力，由此判断纱线是因剪切断裂。当与刀刃接触的纱线受到剪切力而断裂失效后，断裂纱线的应力骤减（图8（a）），与这根纱线交织的纱线上的交织点的挤压也立即减小，应力大幅下降（图8（b））。周围的纱线趋于伸直，布面趋于收紧回复，布面的平均应力水平下降，应变的分布变化与应力同步为正相关。

3.3 冲击系统的能量变化

有限元力学分析中，能量守恒遵循热力学第一定律，整体模型的能量平衡可以表述为：ETOTAL=ALLIE+ALLKE+ALLVD+ALLFD-ALLWK=constant[8]，即：总能量=内能+动能+粘性耗散能+摩擦耗散能-外力功=常量。本模型的这几种能量关系如图9所示。

冲击系统内外力做功为零，系统动能主要是由刀具贡献，且不考虑黏性耗散。由计算完成后的能量历程输出图可以看出，模型的总能量守恒，证明了模拟结果的准确性。正向穿刺过程中刀具的动能被织物吸收，且大部分转化成了织物内能，还有一部分能量由于纱线之间、纱线与刀具间的摩擦作用耗散。刀具反向移动时，织物的内能又转化为刀具的动能，刀具反向速度增加。

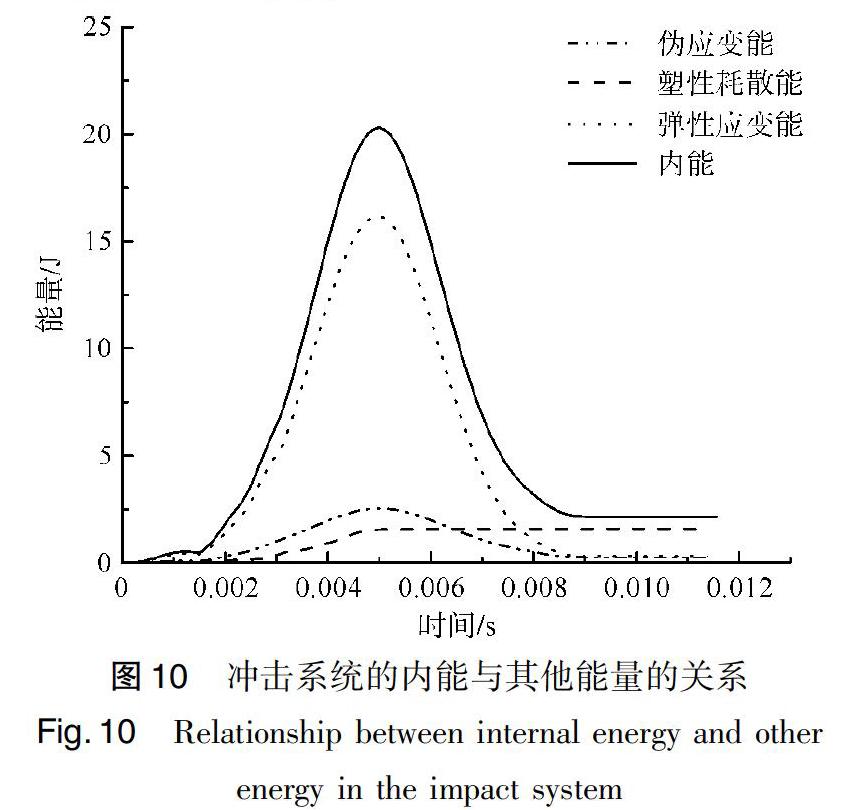
整体模型的内能遵循下式：ALLIE=ALLSE+ALLPD+ALLCD+ALLAE[8]，即：内能=弹性应变能+塑性耗散能+蠕变耗能+伪应变能。这几种能量的关系如图10所示。

由图10可见，弹性形变产生的弹性应变能占了内能的大部分。刀刺织物时，刀具的速度逐渐减小，起初是由于刀具挤压织物导致纱线拉伸产生弹性形变，吸收了刀具大部分的能量，并转化为织物内能，而后某些纱线开始屈服，塑性变形直至失效断裂，这部分的蠕变耗散能与塑性耗散能占比很小。进一步说明刀刺织物时，纱线因拉伸塑性变形断裂的情况很少，主要是受剪切而断裂。也就是说：大部分纱线强度在未达到其抗拉强度时，已经受到剪切作用而破坏。

经计算，图10中伪应变能/内能<10%，根据相关有限元理论[8]，说明控制沙漏变形所消耗的应变能在可接受的范围内，模拟的结果具有可参考性。

4 提高防刺性能的措施

根据有限元软件的模拟结果，可以看出带刃刀具冲击刺破平纹织物的过程包含了顶穿和切割两个方面。要想得到良好的防刺效果，织物必须具有优异的抗剪切和抗拉伸性能，其中抗剪切性能占首要地位。

4.1 提高抗拉伸性能

穿刺过程中，刀具的能量主要转化为纱线形变能（主要是弹性应变能）和摩擦耗散能。因此，优先选用屈服强度极高的纤维纱线，延长布面通过自身弹性形变对刀具能量的吸收的时间;其次，纱线的抗拉强度也尽量要求高。在一定范围内增加纱线表面摩擦因数，从而增加纱线间、纱线与刀具间的摩擦力，可以吸收更多的能量，但是这一部分占比较小，对防刺性能的影响不大，这与文献[9]的实验结果相符。

4.2 提高抗剪切性能

平纹织物纱线的剪切模量、细度、经纬密、组织结构等对其抗剪切性能影响较大，可采用单因素实验与正交实验进一步探寻这些因素的影响。平纹织物的防刺优势在于其良好的弹性回复性能，但是由于纱线间只是简单交织，没有黏结，单根纱线很容易被割断，因此其抗剪切性能不如无纺布，可考虑将机织布与无纺布叠层复合，以发挥两者的优势;或者将平纹基布进行树脂涂层处理[10]，增强织物的防刺性能。

5 结 论

通过准静态穿刺实验，验证了运用有限元方法模拟计算刀具刺穿织物的冲击过程的有效性，对动态穿刺后的布面刺破效果进行仿真，对纱线的应力应变分布进行分析，并得到了冲击系统的能量变化情况，主要结论如下：

1）刀具冲击织物的过程可分为两步：第一，刀具从纱线缝隙中刺入，纱线滑移拉伸，布面变形凸起，刀具速度下降至零;第二，纱线受到剪切或者拉伸作用断裂，布面发生弹性恢复，推动刀具向相反方向移动。

2）织物的应力水平变化与应变同步。布面首先受力凸起，而后回弹，应力水平随之先上升后下降。应力的分布集中在刀尖处、纱线交织点处与布面四周固定端处。当纱线断裂时，断裂纱线应力骤减，与之相交纱线上的交织点处的应力也因此骤减，应变减小，布面略有回弹。

3）刀具的能量少部分通过摩擦耗散，大部分被布面吸收，并转化为纱线的内能。纱线的内能主要由纱线的弹性应变产生，少部分是蠕变和塑性应变能，且断裂点的应力远小于纱线的最大拉伸应力，因此纱线断裂主要由刀具剪切作用导致，提高平纹织物的抗剪切性能是提高其防刺性能的关键。

参考文献：

[1]WANG Q S， SUN R J， TIAN X， et al. Quasi-static puncture resistance behaviors of high-strength polyester fabric for soft body armor [J]. Results in Physics， 2016， 8（18）： 554-560.

[2]裴鵬英， 胡雨， 胡慧娜， 等. 柔性防弹防刺服开发关键技术[J]. 纺织导报， 2017（S1）： 62-65.

PEI Pengying， HU Yu， HU Huina， et al. Key technologies for developing flexible bullet-proof/stabresistant body armor [J]. China Textile Leader， 2017（S1）： 62-65.

[3]马丕波， 蒋高明， 高哲， 等. 纺织结构复合材料冲击拉伸研究进展[J]. 力学进展， 2013， 43（3）： 329-357.

MA Pibo， JIANG Gaoming， GAO Zhe， et al. Advances in impact tensile properties of 3-D textile structural composites [J]. Advances in Mechanics， 2013， 43（3）： 329-357.

[4]王艳飞， 孙耀宁， 孙文磊， 等. 纤维增强复合材料损伤行为及强度预测细观力学建模研究进展[J]. 玻璃钢/复合材料， 2014（6）： 83-89.

WANG Yanfei， SUN Yaoning， SUN Wenlei， et al. Advances of study with micromechanical modeling on damage behavior and strength predication of predication fiber reinforced composites [J]. Fiber Reinforced Plastics/Composites， 2014（6）： 83-89.

[5]施建伟. 基于ABAQUS复合材料层合板渐进损伤有限元分析[D]. 太原： 中北大学， 2015.

SHI Jianwei. Finite Element Analysis of Progressive Damage of Abaqus Composite Laminates [D]. Taiyuan： North University of China， 2015.

[6]周熠， 陈晓钢， 张尚勇， 等. 超高分子质量聚乙烯平纹织物在柔性防弹服中的应用[J]. 纺织学报， 2016， 37（4）： 60-64.

ZHOU Yi， CHEN Xiaogang， ZHANG Shangyong， et al. Application of ultra-high molecular-weight polyethylene plain weave in soft body armour [J]. Journal of Textile Research， 2016， 37（4）： 60-64.

[7]邢京京， 钱晓明. 织物的防刺机制及刀具形状对防刺性能的影响[J]. 纺织学报， 2017， 38（8）： 55-61.

XING Jingjing， QIAN Xiaoming. Stab-resistant mechanism of fabrics and influence of cutter shape on stab resistance [J]. Journal of Textile Research， 2017， 38（8）： 55-61.

[8]庄茁. 基于ABAQUS的有限元分析与应用[M]. 北京： 清华大学出版社， 2012.

ZHUANG Zhuo. Finite Element Analysis and Application Based on ABAQUS [M]. Beijing： Tsinghua University Press， 2012.

[9]张天阳. 机织物防刺性能的有限元分析[D]. 上海： 东华大学， 2012.

ZHANG Tianyang. Finite Element Analysis of Thorn Resistance of Woven Fabrics [D]. Shanghai： Donghua University， 2012.

[10]徐玲玲. 多层芳纶织物增强聚氨酯防刺性能的研究 [D]. 天津： 天津工業大学， 2017.

XU Lingling. Study on the Anti-Stab Performance of Multi-Layer Aramid Fabric Reinforced Polyurethane [D]. Tianjin： Tianjin Polytechnic University， 2017.