一个易错的圆锥曲线结论及其证明


摘 要:本文提供了一个来自焦点三角形面积最大值问题的绝佳反例,以此说明直觉得到的“结论”并不一定准确,并从解析几何的应用技巧上提供了四种不同证法.
关键词:焦点三角形;面积;最大值
作者简介:张日堂(1978-),男,广东阳春人,本科,中学二级教师,研究方向:高考数学教学.
1 问题呈现
问题 已知椭圆x24+y23=1,左右焦点分别为F1和F2,且过点F2的直线交椭圆于A,B两点,求ΔF1AB内切圆半径的取值范围.
2 问题剖析
该问题来源于课本的一道习题,原问题涉及到一个顶点在一个焦点,底边是过另外一个焦点的弦的所谓“焦点三角形”问题,不过原问题是求“焦点三角形”的周长.由椭圆的定义知,“焦点三角形”ΔABF1的周长为定值4a.又因为对任意三角形,其内切圆的半径r,面积SΔ和周长 l之间有关系r=2SΔl,故求内切圆半径的取值范围,即是求△ABF1的面积的取值范围.当直线AB“贴近”x轴时,面积趋向0,所以我们只需确定三角形面积的最大值,问题等价转换成求该“焦点三角形”的面积的最大值,在周长固定的“焦点三角形”中,求其面积的最大值,也变成了一个有意思和有价值的数学问题.由于ΔABF1的面积可以分为ΔAF1F2与ΔBF1F2的面积的和,故三角形的面积的取值范围由yA-yB决定.从直觉来看,在AB⊥x轴时,yA-yB最大,ΔABF1的面积最大.
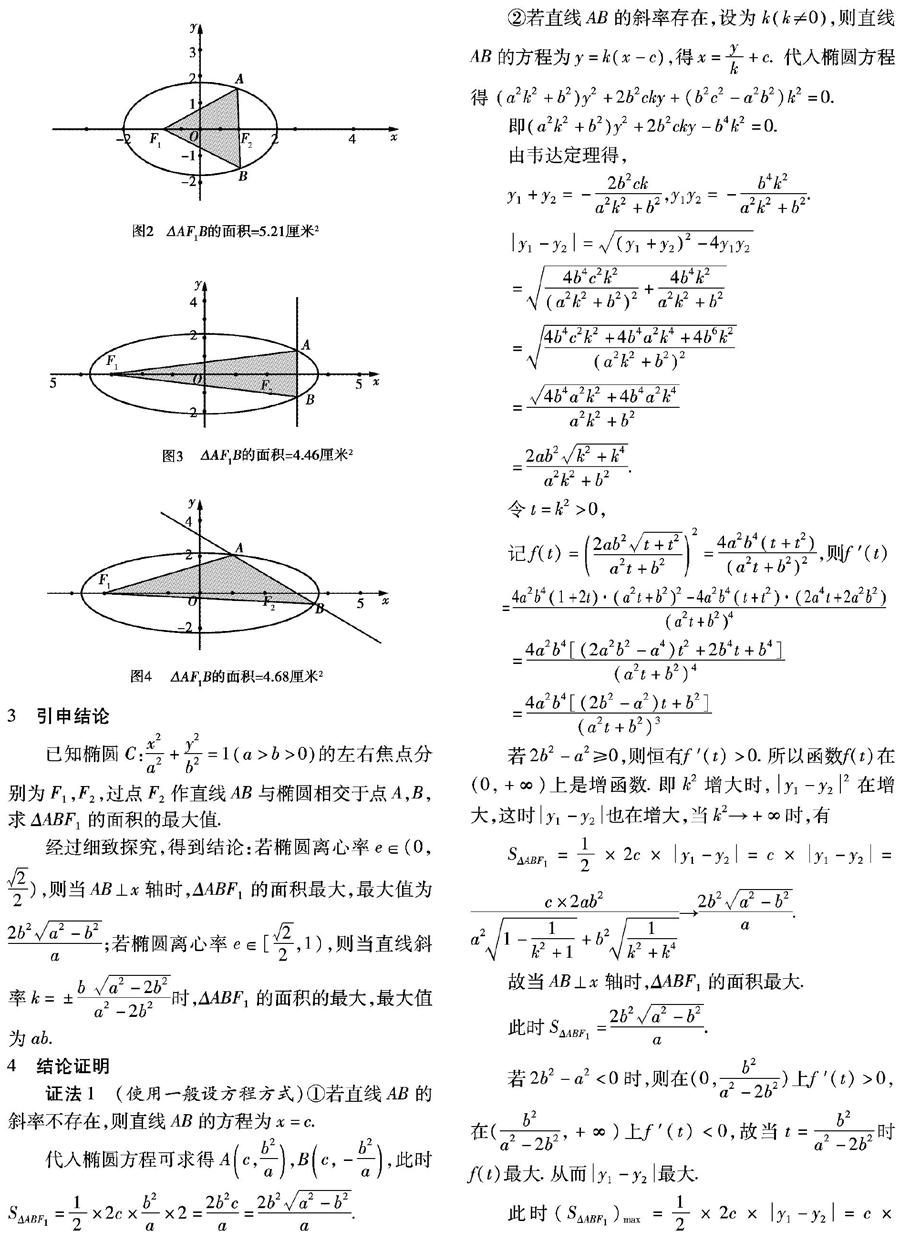
原题中,通过几何画板动态演示(如图1,2对比),可以验证当AB⊥x 轴时,ΔABF1的面积最大.
是否对任意椭圆,都是在AB⊥x轴时,ΔABF1的面积最大?事实上,通过几何画板软件的演示可以发现,当椭圆较“扁”时结论并不正确.如图3,4对比所示,下面情形的三角形面积就不是在AB垂直于x轴时最大,所以原猜想结论并不准确.
3 引申结论
已知椭圆C:x2a2+y2b2=1a>b>0的左右焦点分别为F1,F2,过点F2作直线AB与椭圆相交于点A,B,求ΔABF1的面积的最大值.
经过细致探究,得到结论:若椭圆离心率e∈(0,22),则当AB⊥x轴时,ΔABF1的面积最大,最大值为2b2 a2-b2a;若椭圆离心率e∈[22,1),则当直线斜率k=±ba2-2b2a2-2b2时,ΔABF1的面积的最大,最大值为ab.
4 结论证明
证法1 (使用一般设方程方式)①若直线AB的斜率不存在,则直线AB的方程为x=c.
代入椭圆方程可求得Ac,b2a,Bc,-b2a,此时
SΔABF1=12×2c×b2a×2=2b2ca=2b2 a2-b2a.
②若直线AB的斜率存在,設为kk≠0,则直线AB的方程为y=kx-c,得x=yk+c.代入椭圆方程得 a2k2+b2y2+2b2cky+(b2c2-a2b2)k2=0.
即a2k2+b2y2+2b2cky-b4k2=0.
由韦达定理得,
y1+y2=-2b2cka2k2+b2,y1y2=-b4k2a2k2+b2.
y1-y2=y1+y22-4y1y2
=4b4c2k2a2k2+b22+4b4k2a2k2+b2
=4b4c2k2+4b4a2k4+4b6k2a2k2+b22
=4b4a2k2+4b4a2k4a2k2+b2
=2ab2 k2+k4a2k2+b2.
令t=k2>0,
记f(t)=2ab2 t+t2a2t+b22=4a2b4t+t2a2t+b22,则f ′(t)
=4a2b41+2t·a2t+b22-4a2b4t+t2·2a4t+2a2b2a2t+b24
=4a2b4[(2a2b2-a4)t2+2b4t+b4](a2t+b2)4
=4a2b4[(2b2-a2)t+b2](a2t+b2)3
若2b2-a2≥0,则恒有f ′(t)>0.所以函数f(t)在(0,+∞)上是增函数.即k2增大时,y1-y22在增大,这时y1-y2也在增大,当k2→+∞时,有
SΔABF1=12×2c×y1-y2=c×y1-y2=c×2ab2a2 1-1k2+1+b2 1k2+k4→2b2 a2-b2a.
故当AB⊥x 轴时,ΔABF1的面积最大.
此时SΔABF1=2b2 a2-b2a.
若2b2-a2<0时,则在(0,b2a2-2b2)上f ′(t)>0,在(b2a2-2b2,+∞)上f ′(t)<0,故当t=b2a2-2b2时f(t)最大.从而y1-y2最大.
此时(SΔABF1)max=12×2c×y1-y2=c×y1-y2=2ab2c·a2b2-b42a2b2-2b4=ab.
证法2 (引进倾斜角转换)前面同解法1,记直线AB的倾斜角为α,则tanα=k.
由y1-y2=2ab2 k2+k4a2k2+b2=2ab2 (tan2α+1)tan2αa2tan2α+b2=2ab2c2sinα+b2sinα得,
(1)当b≤c时,由基本不等式得,
y1-y2=2ab2c2sinα+b2sinα≤2ab22 c2sinα·b2sinα=abc.
所以SΔABF1=12×2c×y1-y2≤c·abc=ab,当且仅当c2sinα=b2sinα,即sinα=bc≤1
时,ΔABF1的面积最大,最大值为ab.
(2)当b>c时,记t=sinα(0 f ′(t)=c2-b2t2=c2t2-b2t2<0,故f(t)是减函数,y1-y2=2ab2c2t+b2t是增函数. 所以当sinα→1,y1-y2→2b2a,从而当AB⊥x轴时,ΔABF1的面积最大,最大值为2b2 a2-b2a. 证法3 (改变设直线方程方式)设直线AB的方程为x=ky+c,与方程x2a2+y2b2=1a>b>0联立并整理得, (a2+b2k2)y2+2cb2ky-b4=0. 由韦达定理得, y1+y2=-2cb2ka2+b2k2,y1·y2=-b4a2+b2k2. 所以y1-y2=(y1+y2)2-4y1y2=2b2a1+k2a2+b2k2,SΔABF1=2acb2 1+k2a2+b2k2. 设k2+1=m(m≥1), 则SΔABF1=2acb2 1+k2a2+b2k2=2acb2ma2+b2(m2-1)=2acb2mb2m2+c2=2acb2b2m+c2m. 记函数f(m)=b2m+c2m,则f ′(m)=b2-c2m2=b2(m2-c2b2)m2,当c>b,f(m)最小值2bc,(SΔABF1)max=ab,此时k=±ba;当c≤b,f(m)的最小值为a2,(SABF1)max=2cb2a, 此时k=0. 证法4 (使用直线参数方程)设直线AB的倾斜角为α,则α≠0. 直线AB的参数方程为x=c+tcosα,y=tsinα, (t为参数),代入x2a2+y2b2=1并整理得, (b2+c2sin2α)t2+2cb2cosα·t-b4=0. 由韦达定理得, t1+t2=-2cb2cosαb2+c2sin2α,t1t2=-b4b2+c2sin2α. 所以t1-t2=(t1+t2)2-4t1t2 =4b4c2cos2α(b2+c2sin2α)2+4b4b2+c2sin2α =2ab2b2+c2sin2α. SΔABF1=SΔAF1F2+SΔBF1F2=ct1-t2sinα=2ab2csinαb2+c2sin2α=2ab2cb2sinα+c2sinα. (1)當b≤c时,SΔABF1≤2ab2c2 c2sinα·b2sinα=ab(当且仅当c2sinα=b2sinα,即 sinα=bc≤1时等号成立). (2)当b>c时,c2sinα+b2sinα=c2sinα+c2sinα+b2-c2sinα≥2c2+b2-c2sinα ≥2c2+b2-c2=a2(当且仅当sinα=1时等号成立). 所以SΔABF1=2ab2cb2sinα+c2sinα≤2b2 a2-b2a. 参考文献: [1]徐俊峰. 椭圆中焦点三角形问题的求解策略J.数学之友,2014(03):76-77+79. [2]斯理炯. 高中数学竞赛专家讲座——解析几何 M.杭州:浙江大学出版社,2018. (收稿日期:2019-07-07)

