煤矿安全监控中信息融合技术的应用研究

冯韶元

（郑煤集团告成煤矿通风科，河南 登封 452477）

近些年来，随着科技的持续发展，信息技术被广泛应用于煤矿安全监控。当前，信息融合技术在医学、图像识别、AI等领域得到应用，我国在信息融合技术领域也获得了丰硕的成果。越来越多的专家和学者开始关注信息融合技术在煤矿安全监控中的应用，利用布置在矿井下的各种传感器获取所需信息，利用信息融合技术提高煤矿安全监控的准确性，有效避免煤矿安全事故的发生。在现阶段的煤矿安全监控系统中，信息融合技术的应用越来越广泛，如基于神经网络的煤矿安全监控、基于模糊逻辑的煤矿安全监控等[1]。这些信息融合技术各有优点，但也存在缺点，因为煤矿生产环境复杂多变，很难构建确切的数学模型，而且煤矿生产的相关数据量很大，要求监控系统具备学习能力。因此，本研究提出结合模糊逻辑和神经网络构建信息融合预测模型，以期实现煤矿安全监控。

1 煤矿安全监控预测总体方案

本次研究的煤矿安全监控总体方案结构如图1所示。本次研究的重点是信息融合预测模型。

如图1所示，煤矿安全监控系统通过数据库实时监控煤矿矿井中的传感器信息，借助信息融合模型判定煤矿的安全等级，及时预警可能发生的煤矿安全隐患。本次研究针对矿井安全生产中的瓦斯、风速、粉尘这三种信息数据构建信息融合模型。合理的风速有助于降低瓦斯浓度，还可以给煤矿生产人员提供足够的氧气；但风速过大会导致粉尘浓度上升，增加煤矿粉尘爆炸风险。瓦斯、风速、粉尘之间存在非线性关系，三种信息数据的有效融合可以提高煤矿安全预测准确度。本次研究的信息融合预测模型选用二级结构。其中，一级融合基于自适应加权算法实现融合，以获取同类传感器权重值，提升信息表述精度。二级融合模型是基于模糊神经网络的模型，因为矿井下生产环境复杂，很难构建精确的数学模型，同时需要同时处理大量数据。

2 信息融合预测模型研究

2.1 信息融合预测模型设计分析

为了有效监控煤矿生产，减少煤矿事故的发生率，生产企业就应该设法降低矿井下的瓦斯、粉尘等危险物质的浓度。因此，矿井下的通风非常重要，合理的通风能够及时有效避免瓦斯积聚，降低瓦斯浓度，同时提供足够的氧气。煤矿安全生产的基本原则之一便是“以风定产”。然而，风速过大会导致粉尘浓度上升，增加煤尘爆炸风险。基于此，本次研究选取了风速、瓦斯、粉尘这三个相互影响、相互制约的传感器信息加以融合，提出如图2所示的信息融合预测模型。

图1 煤矿安全监控总体方案

图2 信息融合预测模型

该信息融合模型分为两级，第一级信息融合基于自适应加权算法，第二级基于模糊神经网络。一级融合目的是通过确定多个同类传感器的权重值，提高对风速、瓦斯、粉尘等监控预测对象的表述精度。采用基于模糊神经网络的二级融合模型的原因是考虑到煤矿生产环境的复杂性，难以构建精确的数学模型，且数据繁多，需要根据矿井实际情况设置相应的报警等级，需要结合生产实际设置大量的模糊数据[2]。此外，矿井下环境变化频繁，信息融合模型需要具备一定的学习能力，才能根据数据变化做出相应调整。因此，本文基于神经网络理论提出基于模糊神经网络的二级信息融合模型。

通过第一级模型对风速、瓦斯、粉尘这三类信息进行融合处理，判断其是否超出《煤矿安全规程》的相关标准，如果其中任意一类传感器数据超标则直接做出预警，不必经过二级融合。如果未监测到数据超标，则对数据进行归一化处理，再通过二级融合模型融合各项数据，判断是否超标。

2.2 一级融合模型

2.2.1 自适应加权融合算法

煤矿安全监控系统中的一级信息融合步骤：第一步，根据自适应加权算法获取传感器权重；第二部，加权处理获得精确权重值；第三步，归一化处理数据。自适应加权算法按照数据精度确权，精度越高，权重越高。为提升数据精确度，需要将数据乘以相应权数，再做计算均值。为了准确反映煤矿安全监控指标数据，需要布设多个相同类型的传感器，以获得对同一个对象的精确值。

例如，某矿井巷道布设有四个监测瓦斯浓度的传感器、一个监测粉尘浓度的传感器、一个监测风速的传感器。四个瓦斯传感器共同获取该巷道的瓦斯浓度数据，各瓦斯传感器位置、精度不同，权重值不同。因此，需要获得这四个传感器的对应权重值，从而提升瓦斯浓度的精确度。为获得各个瓦斯传感器的最优权重值，需要多次测量它们采集的数据并对数据进行处理。也就是说，在确保总均方差最小的情况下，根据自适应加权算法求取各个传感器对应的权重值。

总均方差为：

其中，i、j表示瓦斯传感器编号，由于X1、X2、X3、X4相互独立，则：

总方差σ2可写成：

根据式（4）可知，σ2是多元二次函数，包括多个加权因子，其中必然存在一个最小值，求解出这个最小值就等于求解加权因子，其满足式（1）中的函数极值。根据函数极值求解方法进行计算，人们可以发现，当加权因子为时，方差最小，即：

以上是对各传感器进行一次测量所获数据的估计。在实际应用中需要对第i个瓦斯传感器进行k次测量，以求出最优加权因子。此时，k次测量的均值为：

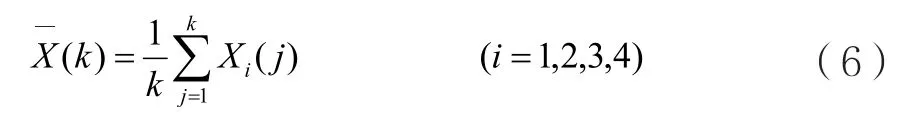
此时的信息融合值为：

同理，可以根据函数极值的求解方法，计算出最小均方差，即：

由于k永远大于1，因此当k值不断增长 时，将不断减小，理论上来说k越大，数据融合值精度越高。但实际上k值也不能太大，因为k值持续增长时，自适应加权算法将不断趋近算术平均值法。

2.2.2 最优权重值计算

如上所述，多个传感器自适应加权融合基本步骤是：（1）求传感器k次测量数据的平均值；（2）求得传感器i的方差（3）根据公式求最优加权因子Wi；（4）得到融合值

本文选取监测瓦斯浓度的多个传感器在某时间点测量7次后获得的数据，依照上述步骤计算最优权重值，首先求得各个传感器多次测量所获数据的平均值、权值及方差，如表1所示。

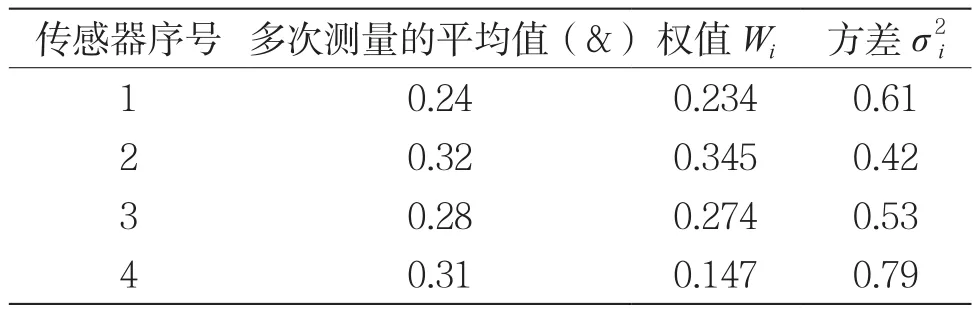
表1 传感器权值数据

根据表2可知，四个瓦斯传感器的权值不同。因此，可以计算此时煤矿巷道的瓦斯浓度融合值：

在实际煤矿生产中，企业往往需要设置多个传感器监测一个指标，需要用自适应加权算法确定多个同类传感器的权重值。

2.2.3 归一化处理

利用上述方法求得传感器权重值，得到更加精确的数据，为了方便进行二级信息融合，人们还必须对精确数据进行归一化处理，具体公式如下：

式中，x归一为某类传感器数据经过归一化处理后的数值；为某类传感器数据进行自适应加权融合后的数值；为进行自适应加权一级融合后传感器样本数据的最小值；为自适应加权一级融合后传感器样本数据最大值，到此，第一级融合处理完成。

2.3 基于模糊神经网络的二级融合模型

2.3.1 确立模糊推理预测系统

如上所述，选择风速、瓦斯、粉尘这三个关键的煤矿安全信息作为融合信息来源。可见，基于模糊神经网络的二级融合模型输入变量有三个。模型输出变量即模型预测结果，也就是煤矿当前安全等级：安全、中等、危险[3]。“安全”等级表示矿井下非常安全，出现安全事故的可能性很小；“中等”等级表示矿井下安全环境一般，需要加强监测；“危险”等级则代表当前矿井下发生安全事故的可能性较高，必须马上中止生产活动，仔细排查安全隐患。本次研究通过实地调查、查阅文献资料等方式，以某煤矿为例，得到风速、瓦斯、粉尘这三个信息与煤矿安全等级的关系，如表2所示

针对风速、瓦斯、粉尘这三种输入变量，根据其测量数值大小与煤矿矿井实际生产情况，对数值进行归一化处理后，分成三个模糊子集：{高、中、低}。选取高斯函数作为各模糊子集的隶属度函数，将各类传感器的测量数据进行归一化处理得到具体的隶属度。

模糊推理的规则形式一般为“IF...THEN...”。结合某煤矿生产实践，人们可以确立合理的模糊推理规则，例如，“IF（风速高）AND（瓦斯浓度高）AND（粉尘浓度高）THEN（安全等级为危险）”。规则中的高、中、低是风速、瓦斯浓度、粉尘浓度的模糊量化等级，可使用具体分值“1”“0.5”“0”来量化煤矿安全等级。

模糊推理的规则往往有很多条，制定规则的基本原则是规则必须涵盖一切可能出现的情况。相同的规则可合并但不能出现相互冲突的规则。根据风速、瓦斯、粉尘这三个输入变量，考虑一切可能发生的情况，可以将矿井下模糊推理规则设置为27条。

表2 风速、瓦斯、粉尘与煤矿安全等级的关系

2.3.2 构建模糊神经网络模型

煤矿监控预测模型的核心是基于模糊神经网络的信息融合模型。首先利用煤矿矿井的实际生产数据训练基于模糊神经网络的信息融合模型。训练结束后，此模型具备了学习能力，可以根据矿井下的各项数据对煤矿安全等级进行及时准确的预测。基于模糊神经网络的融合模型包括五层。

（1）输入层。该层包括代表各项指标信息的节点，负责将传感器数据传递至下一层。

（2）模糊化层。该层包括代表各个输入量模糊子集的节点，负责获取输入量属于某模糊子集的隶属度。本次研究的隶属度函数选取高斯型函数，如式（11）所示：

式中，为隶属度，cij为隶属函数中心。

（3）规则层。该层包括代表根据矿井实际情况制定的27条模糊推理规则的节点，各节点输入为模糊子集隶属度，输出为匹配度。其主要作用是计算模糊规则的合适度。

（4）归一化层。该层总共有27个节点，其主要作用是对数据进行归一化处理。

（5）输出层。该层只有一个节点，用于完成解模糊功能，为模型输出值，期望输出值设为0、0.5、1，分别代表煤矿安全、中等、危险这三个安全等级。

在二级信息融合模型中除了归一化层、输出层之外，其他层的权值均设为1，而归一化层、输出层之间的权值设为Wij。按照模糊推理规则，人们可以构建模糊化层和隐层之间的连接关系，并通过数据训练持续优化模糊化层的隶属度函数值，不断完善模型，以提升模型输出值的精度。

2.4 模糊神经网络模型的训练算法

BP算法是现阶段应用最广泛的模糊神经网络训练算法。BP算法的应用推动了多层前馈神经网络的发展与应用，形成使用广泛的BP神经网络。现阶段，大部分关于神经网络的训练算法均为基于BP算法进行改进所得。经典三层BP网络包含输入层、隐层、输出层，结构如图3所示

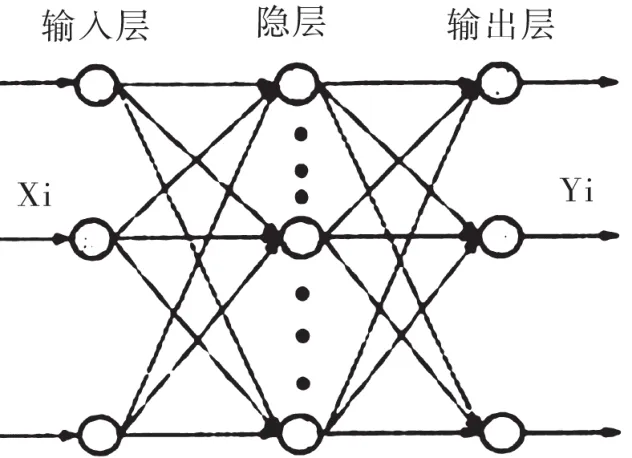
图3 经典三层BP网络建结构

BP算法存在两个主要缺陷：易陷入局部极小点；收敛速度慢。煤矿矿井环境复杂多变，会产生大量数据，对于预测的速度要求很高。传统BP算法无法满足其预测速度。因此，必须基于传统BP算法进行相应改进，以显著提升BP算法的速度。在此背景下，一些改进算法被相继提出，如传牛顿法、变步长算法、附加动量法等，这些算法可以提高算法运算速度，但是也存在较多问题，而且对训练速度的提升效果不明显。而将数值优化算法（LM）与BP算法结合开展网络训练的算法被人们称为LMBP算法。当网络权重个数在几百以内时，LMBP算法的收敛速度明显优于其他传统改进算法，相比传统BP算法的收敛速度更是有显著提升。实际上，数值优化算法LM是基于牛顿法变形而来的一种高效算法，非常适合用来训练指标指数是均方误差的网络。而BP算法正需要将输出与实际输出信号之间的误差平方和控制在最小，因此结合LM算法与BP算法可以有效调整传统BP算法收敛速度。

3 结语

本次研究提出了一种二级信息融合模型，用于对煤矿安全状况进行准确预测，通过经过优化的信息融合算法来提升煤矿安全预测的精度和速度。笔者分析了信息融合预测技术在煤矿安全监控预测中的应用现状和应用必要性，提出一种二级结构的信息融合模型。其中，第一级结构采用自适应加权算法获取多个同类传感器的权重系数，以提升传感器的表述精度；第二级融合模型基于模糊神经网络，解决矿井安全环境难以建立精确数学模型的问题，同时模型具备学习能力，符合煤矿矿井实际生产情况。