拟对角扩张C*-代数Cuntz半群的性质

方燕

(上海海事大学文理学院，上海 201306)

0 引 言

Cuntz半群的性质作为C*-代数的正则性质，在C*-代数的分类中有重要的应用。TOMS[1]给出两个不同构的单的AH代数，它们的Cuntz半群不同,其中只有一个具有弱无孔性质，但它们的Elliott不变量相同。这说明如果不能用Elliott不变量区分C*-代数则可以通过它们的Cuntz半群来区分。

1 预备知识

定义1[3]称一个序半群M是无孔的，是指对于任意的非零元a,b∈M，存在自然数n满足na≤nb，则有a≤b。

定义2[4]称一个序半群M具有弱可分性质，是指对于任意的a,b∈M，如果2a≤a+b≤2b,则可以得到a≤b。

定义3[5-6]称一个序半群M具有Riesz插值性质，是指对于任意的a1,a2,b1,b2∈M，如果ai≤bj,则存在某个c∈M，使得ai≤c≤bj,i,j=1,2。

称一个C*-代数A具有无孔的性质，是指A的Cuntz半群W(A)具有弱无孔的性质。称一个C*-代数A具有弱可分性质，是指A的Cuntz半群W(A)具有弱可分性质。称一个C*-代数A具有Riesz插值性质，是指A的Cuntz半群W(A)具有Riesz插值性质。

W(A)∶=M∞(A)+/～

定理1[3]设A是一个C*-代数,则下面的结论等价:(1)a≤b;(2)对于任意的ε>0,(a-ε)+≤b;(3)对于任意的ε>0,存在δ>0,使得(a-ε)+≤(b-δ)+。

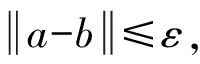
((1-Pn)⊗1k)a(((1-Pn)⊗1k)-ε/2)+≤

((1-pn)⊗1k)b(((1-pn)⊗1k)-ε/4)+

2 主要结果

证明只要证明W(B)具有无孔性质即可，即对于任意的非零元a,b∈W(B)，存在自然数n满足na≤nb，只要证明a≤b即可。由定理1,只要证明对于任意的ε>0,(a-ε)+≤b即可。

由定理2有

(a-ε/2)+≤PnaPn+

((1-Pn)a(1-Pn)-ε/4)+

(b-ε/2)+≤PnbPn+

((1-Pn)b(1-Pn)-ε/4)+

因为na≤nb,所以有n(PnaPn-ε/2)+≤nPnbPn。

因为PnaPn和PnbPn都在I中，并且I具有弱无孔性质，所以有(pnapn-ε/2)+≤pnbp。

同时有nπ(a)≤nπ(b)成立。因为A具有弱可比性质，所以有π(a)≤π(b)。由引理1得到((1-pn)a(1-pn)-ε/2)+≤((1-pn)b(1-pn)-ε/4)+因此可得到

(a-2ε)+≤(PnaPn-ε/2)++

((1-Pn)a(1-Pn)-ε/2)+≤

pnbpn+((1-pn)b(1-pn)-ε/4)+≤b

证明只要证明W(B)具有弱可分性质即可，即对于任意的a,b∈W(B)，如果2a≤a+b≤2b，只要证明a≤b即可。由定理1,只要证明对于任意的ε>0,(a-ε)+≤b即可。

由定理2有(a-ε/2)+≤pnapn+((1-pn)a(1-pn)-ε/4)+。因为2a≤a+b≤2b,所以有2(pnapn-ε)+≤(pnapn-ε)++pnbpn≤2pnbpn。因为pnapn和pnbpn在I中,并且I具有弱可分性质，所以(pnapn-ε)+≤pnbpn。同时因为2π(a)≤π(a)+π(b)≤2π(b),并且A具有弱可分性质，所以π(a)≤π(b)。由引理1有((1-pn)a(1-pn)-ε/2)+≤((1-pn)b(1-pn)-ε/4)+,因此(a-2ε)+≤(pnapn-ε)++((1-pn)a(1-pn)-ε/2)+≤pnbpn+((1-pn)b(1-pn)-ε/4)+≤b。

证明只要证明W(B)具有Riesz插值性质即可，即对于任意的a1,a2,b1,b2∈W(B)，如果ai≤bj,只要证明存在c∈W(B)使得ai≤c≤bj即可,i,j=1,2。

其中i,j=1,2。

由定理2有(ai-ε/2)+≤pnaipn+((1-pn)ai(1-pn)-ε/4)+,其中i,j=1,2。因为ai≤bj,所以有(pnaipn-ε)+≤bj,i,j=1,2。

因为pnaipn和pnbjpn(i,j=1,2)在I中,并且I具有Riesz插值性质，所以存在c∈I+使得(pnaipn-ε)+≤c≤(pnbjpn-ε)+,i,j=1,2。因为ai≤bj,所以有π(ai)≤π(bj),并且A具有Riesz插值性质，因此存在d∈B+使得π(ai)≤π(d)≤π(bj),i,j=1,2。

由引理1有

((1-pn)ai(1-pn)-ε/2)+≤

((1-pn)d(1-pn)-ε/2)+

((1-pn)d(1-pn)-ε/2)+≤

((1-pn)bj(1-pn)-ε/2)+

取e=c⊕((1-pn)d(1-pn)-ε/4)+，因此有

(ai-2ε)+≤

(pnaipn-ε)++((1-pn)ai(1-pn)-ε/2)+≤

c+((1-pn)ai(1-pn)-ε/2)+≤

c+((1-pn)d(1-pn)-ε/4)+≤

pnbpn+((1-pn)bj(1-pn)-ε/8)+≤bj