基于应用的《体育统计学》教学模式及相关问题思考

许 玮

（南京邮电大学体育部，江苏 南京 210071）

体育统计学是体育院系开设的一门主干课程。该课程要求学生具备一定的数理基础，而体育专业的学生的数理基础相对薄弱。因此，体育统计学的教学效果差和学生的定量思维能力难以培养的问题一直困扰着授课教师。笔者通过多年的体育统计学教学实践发现，传统教学模式不利于学生定量思维能力的培养，亟待通过创新体育统计学教学模式，改善体育统计学教学效果。传统教学模式是一种“方法先入”的教学模式，即把统计学教学看成是方法学习的过程，从而过多地强调方法学习本身，而忽略方法背后的统计学本质——统计思想的教学。这种教学模式有三个弊端：一是方法的学习与方法的应用相割裂；二是让学生误认为为统计学习就是学习统计公式，统计应用就是应用统计软件；三是易让数理基础差的学生产生厌学情绪。

本文通过案例分析和比较分析方法，阐释“基于应用”的《体育统计学》教学模式的内涵、特征和优势。以方差分析、因子分析为教学案例，剖析“基于应用”的统计学教学模式的基本原理，演示相应的教学过程，并针对该方法在实际教学运用中需要注意的几个问题进行深入探讨。

1 基于应用的《体育统计学》教学的模式内涵

基于应用的《体育统计学》教学模式，不能简单地理解为“将统计学方法应用于实际问题”，而应该理解为“从应用的视角”去解读“统计方法”，进而理解统计方法的确切涵义，从而达到培养学生定量思维的目的。

基于应用的《体育统计学》教学过程与解读统计方法的形成过程相一致。遵循“提出问题-分析问题-解决问题”的逻辑路径。统计学源于“解决问题”的需要而产生。因而，在课堂教学中应该充分重视面向“实际问题解决”的教学方法。换句话说，统计方法的产生源于“解决实际问题”需要，如果在学习方法的时候再回到“问题解决”这个起点上来，就很容易掌握统计方法的本质。它不仅可以避免陷入“死记公式”的陷阱，还可增加统计方法学习的趣味性。

下面我们以“单因素方差分析”为例来说明“基于应用”的体育统计学教学模式。为了考察单因素A的影响，分m个水平进行试验，数据结构如表1所示。

表1 单因素方差分析数据结构

1.1 传统教学模式下的方差分析教学过程单因素方差分析的关键在于理解离差平方和的关系。按照单因素方差分析理论可以将它们分为三个部分：总离差平方和，误差项离差平方和以及水平项离差平方和[1]。在传统的教学方法中，我们会推演总平方和是如何分解为误差项平方和与水平项平方和的。总离差平方和,水平离差平方和。通过对SST式进行分解，得到两个部分是SSA和SSE之和，从而有SST=SSA+SSE的结论。这样的拆解公式会让数理功底不好的初学者难以理解每部分的含义。

1.2 “基于应用”的教学模式下方差分析教学从应用角度看，方差分析的主要目的是比较多组均值是否相等的问题，对于例1中的数据，就是比较因素A的m个水平所产生的影响是否相同，而均值是否相等取决于变异部分。因此，方差分析最终又归结到对变异进行分解的过程[2]。直观上来看，上表数据变异主要来源于两个部分，一是A因素引起的变异，二是随机因素引起的变异（通常用字母E来表示）。这一区分直接引导我们对数据的变异进行分解。在分解变异之前，需要知道如何度量变异。在方差分析中，变异的度量主要是借助“离差平方和”来实现。接下来要做的工作是对各个部分的变异进行度量。总变异SST实际就是各个数据通总均值的比较而获得，即。SSA可理解为消除掉个体随机变异的影响后便是SSA。现在，我们假设没有随机部分的影响，即随机变异为零，那么就有SSA=SST。具体而言，我们将每组数据均以各组的均值来代替，实际上就是消除了随机部分的影响（见表2）,此时总变异为

表2 消除了随机因素影响的数据结构

同样的道理，我们假设因素A没有影响，那么剩下的变异便是随机变异SSE，数据结构见表3。此时，总变异部分。最后，我们通过表1-表3的对比发现，表2和表3的数据相合并正好等于表1的原始数据。这就间接地证明了SST=SSA+SSE。由此可见，基于应用的《体育统计学》教学模式的优点是直观思维，避开公式推导，让每一步分解都具有实际意义。即使是数理基础不好的初学者，也能很快掌握方差分析方法的精髓。

表3 消除了A因素影响后的数据结构

2 “基于应用”的《体育统计学》教学中的几点思考

基于应用的体育统计学教学实质就是从实际应用出发来阐释统计学理论。让学生们带着实际问题来学习统计学，让理论学习变得直观而易于理解。在学生基本掌握了统计方法之后，我们再从传统的理论教学进路来演示统计学方法，这一过程让学生明白理论推导和应用之间的一致性，同时在统计理论上也有一个提高。前文的例子中，我们可以回到总离差平方和的代数式分解，代数式分解结果与我们“基于应用”视角进行的分析具有一致性。“基于应用”的统计学教学模式，虽然具有诸多优点，但在实际教学中，对于教师提出了更高的要求。

2.1 教师要透彻理解统计思想统计学的本质是方法背后的统计思想[3]。统计思想是为解决某一问题而提出来的思维方式，而此方法经理论化、模型化以后可以解决一大类问题。可以说，统计思想实际上是解决实际问题的一种思维方式的概念化（Generalize）。统计思想是统计方法的灵魂，如果抽掉统计思想这一内核，统计学只剩下公式的推演和证明，那么统计学就与数学没有多大区别。

如果教师在课堂教学中不对统计思想讲解透彻，就会给学生理解统计方法和学习统计原理带来很大的困难。教师应该对一种方法的“统计思想”有深刻的理解，才能够在教学中运用自如，而不至于在方法的“汪洋”中迷失方向，也只有如此，才能让学生在统计学的课堂中抓住统计方法的灵魂。例如，在上述的方差分析中，理解了方差分析的“统计思想”就是“分解变异”时，就掌握了方差分析方法的精髓。适用于方差分析的实际问题可能千变万化，但万变不离其宗，只要我们牢牢掌握了该方法的统计思想，问题就可迎刃而解。

2.2 统计学教学中的“去数学化”前已述及，统计学的内核在统计思想，而统计学方法本身呈现给我们的是抽象的数学符号。面向数理功底较差的学生授课时，如何在讲解中，将统计方法“去数学化”显得很重要。所谓的“去数学化”实际就是将统计方法呈现给我们的抽象数学形式，转换成我们易于理解的语言过程。“去数学化”也是对统计方法背后的统计思想的进一步细化和具体化。我们以因子分析为例来说明“去数学化”的重要性。

因子分析模型的解析表达式通常有如下的形式：假定P个随机观测向量，有均值，协方差，因子分析的模型可表达如下形式[4]：

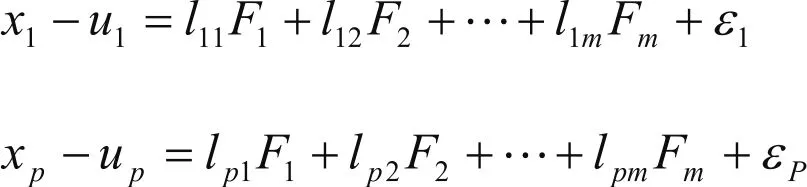
其中m个公共因子F1，F2…Fm和特殊因子，组成。若用矩阵表示，则是这一高度“数学化”的模型，往往让文科学习者“如坠云雾”。

如何理解这一模型呢？我们在采用“基于应用”的统计学教学方法的时候，就需要对这一数学公式进行“口语化”转译。当然，转译的前提仍然是对因子分析统计思想有深刻的理解。因子分析模型的提出是基于这样一种想法，即“希望用几个潜在的，但不能观测到的随机变量去描述许多变量间的协方差关系”（这几个潜在但不能观测的随机变量被称为因子）。这里可以从两个视角进行阐释：一是从数据结构出发，我们可以认为因子分析要做的是通过线性变换，来重新表达数据结构，它希望变换后可以用少数因子来反映原数据的大部分信息。信息用什么来衡量？显然就是这里的“协方差逼近”（Covariance Approximation）；也即是说如果数据线性变换后的数据协方差应该与原数据的协方差结构逼近。另一个视角是从数据相关性角度出发，我们可以认为因子分析是用变量间的相关性对数据进行重新分组，组内高度相关，而组间相关性较低。各组内变量象征有单一潜在的结构（因子）对观察到的相关负责。前者更接近于数学表达式，后一种则更接近于实际应用。但无论是哪种视角去理解因子分析模型，最终都回到了“协方差逼近”上来。因子分析实质上也是一种统计变换，变换后的数据可以用少数因子来表达原数据结构的大部分信息。正是因为这一原因，很多教材也把因子分析看成是一种数据“降维”技术[5]。至此，我们基本理解了因子分析模型的数学表达式的含义,F代表“因子”，L代表“因子”的重要性程度（因子载荷）。

在课堂教学中，通过上述讲解后，学生就会理解因子分析模型中每个符号都代表实际意义，因子分析的每一步分解也有相对应的价值。故而，在吃透统计思想的前提下实现将“用数学语言”表达的统计方法，转换成我们能理解的表达方式（即去数学化），能取得更好的教学效果。

2.3 充分认识“统计距离”的重要性基于应用的《体育统计学》教学过程中，除了要充分理解方法本身所蕴含的统计思想外，还需要清楚具体统计方法是如何实现“统计思想”的。这就需要理解“统计距离”的概念及其表达的含义。它构成了“统计思想”与“统计方法”之间的桥梁。

“统计距离”与通常所用的“欧式距离”有相似的含义，都是度量两点间差异性（或者数据的变异）。之所以提出“统计距离”的概念是因为有时候“欧式距离”并不能有效地度量两点间的距离。例如在p维空间中的点在各个维度上“变差”（Variance）是不同，而“欧氏距离”未考虑这种变差的影响，而是将各个维度上的“重要性”等同看待。而“统计距离”在度量距离的时候，将各个维度上的“变差”考虑进去，从而能更准确地测度“数据变异”。

3 结 语

通过比较传统教学方法与基于应用的统计学教学模式的优劣，可知传统教学模式强调“方法先入”，其弊端是统计理论学习与统计应用相分离、学习统计原理变成了“死记公式”，甚至还会让学生对体育统计学产生厌学心理。而基于应用为导向的教学模式，注重对统计方法背后统计思维过程的解析，从应用的视角，来解读统计公式所表达的直观含义，让学生更快地掌握统计学方法的精髓。但基于应用的《体育统计学》教学对教师的要求更高，教师不仅要对统计理论和方法的本质做到了然于胸，善用“统计距离”链接“统计思想”与“具体统计方法”，搭建一座桥梁，帮助学生理解如何实现从“统计思想”构建“统计方法”。同时，在运用基于应用的《体育统计学》教学模式时，尽量做到“去数学化”处理。总之，基于应用的《体育统计学》教学模式教学效果的取得，很大程度上取决于老师对《体育统计学》中相关统计方法的理解和教学方法的灵活运用。