管道钢材与陶瓷涂层界面残余应力分布的有限元分析
王瑞英
海洋石油工程股份有限公司,天津 300451
管道钢材的表面性状对管道钢材的性能具有重要的影响,采用陶瓷涂层改性管道钢材表面是目前改善管道钢材性能的重要途径,钢材表面热喷涂技术是常用的钢材表面改性方法之一[1]。然而由于涂层与基体母材物性参数存在差异,在二者界面上存在较大的残余应力,降低了涂层与基体母材的结合强度,易导致涂层剥落,限定了热喷涂技术的应用范围。对涂层结合处残余应力进行有限元分析,可明确涂层的应力大小、分布以及引起残余应力的原因,这对采取措施以增强涂层结合力,提高涂层使用寿命具有指导意义。
1 有限元模型
1.1 模型建立与网格划分
(1)模型建立。计算所用试样基体为45#钢管,规格为φ15 mm×5 mm;涂层材料选用Al2O3-13%TiO2(简称AT涂层)和NiCr-Cr3C2两种陶瓷材料;过渡层材料为镍包铝,涂层厚度300 μm。沿试样直径方向取一矩形剖面,长7.5 mm,进行二维有限元应力分析。考虑到对称性,以该截面的1/2作为分析模型,其坐标系的选取见图1。为便于有限元分析,作了如下假设:
第一,因试样较薄,忽略了试样内的温度差异、试压应力;试样表面温度为室温,约定为20℃。
第二,涂层内的孔隙直径远小于涂层厚度,因此在模型中不考虑孔隙的影响[2]。
第三,管壁基体及涂层材料均为各向同性[2],且不考虑温度对其物性参数的影响。
第四,喷涂距离很短,认为粒子在等离子喷涂过程中匀速飞行,速度为0.5 km/s。

图1 有限元分析模型
第五,因涂层组织呈层状结构,喷涂粒子由球状变为饼状,基体不变形。
第六,喷涂过程中粒子不反弹,略去冲击过程中热能和机械能的损失[3]。
(2)网格划分。因为主要目的是分析涂层结合界面处的残余应力,因此为了得到精确结果,减少多余计算,本文采用不均匀网格划分,即在涂层与基体母材界面处采用细网格划分,远离界面处用粗网格划分。
1.2 物性参数的确定
查阅材料手册,借助简单混合比法则[4],确定涂层、过渡层与基体的物性参数,见表1。

表1 材料物性参数(不考虑温度的影响)
2 残余应力的计算
2.1 粒子撞击力的计算
等离子喷涂过程中,喷涂粒子对基体母材有撞击力,并以压应力的形式存在于涂层内部。因为撞击过程瞬间完成,因此不能用动量守恒定律来计算此压应力,只能借助能量法。根据机械能守恒定律和广义胡克定律得:

式中:m为一个粒子的质量,kg,m=(4/3) ρπR3;ρ为粒子密度,kg/m3;R为粒子半径,m;V0为粒子初始速度,m/s;g为重力加速度,m/s2,取10;d表示喷涂距离,m;F表示一个粒子对基体的撞击力,N;S为一个粒子的变形量,m。
式(1)表示喷涂粒子在冲击过程中减少的重力势能和动能,将全部转化为粒子自身的弹性应变能。喷涂粒子平均直径D为40 μm,其到达基体表面后,由于撞击力,由球形变为饼状,为便于计算,约定S为20 μm,由质量守恒定律,可知饼状喷涂粒子直径约为1.2D。但由于涂层实际厚度为300 μm,撞击后一个粒子的平均有效厚度只有20 μm,因此需要15个喷涂粒子作用在一个喷涂粒子的撞击面积上,才能达到要求涂层的厚度。因此,涂层上的压应力为:

式中:σ为涂层单位面积上的压应力,N/m2;D为喷涂粒子平均直径,m。
根据(2)式计算解得,AT涂层上表面的平均压应力为0.422×106N/m2;添加过渡层后,AT涂层上表面的平均压应力为1.225×106N/m2。
2.2 单层涂层残余应力的计算
AT涂层试样在不同边界条件下的应力计算结果如图2~5所示。由图2可知,在只考虑温度因素时,基体内部残余应力分布均匀,且应力值很小,在基体与涂层界面上存在着一个很大的应力突变,并且界面处应力值很大。这是因为涂层与基体物性参数存在很大差异,界面处由于变形的协调性,存在较大的应力集中。
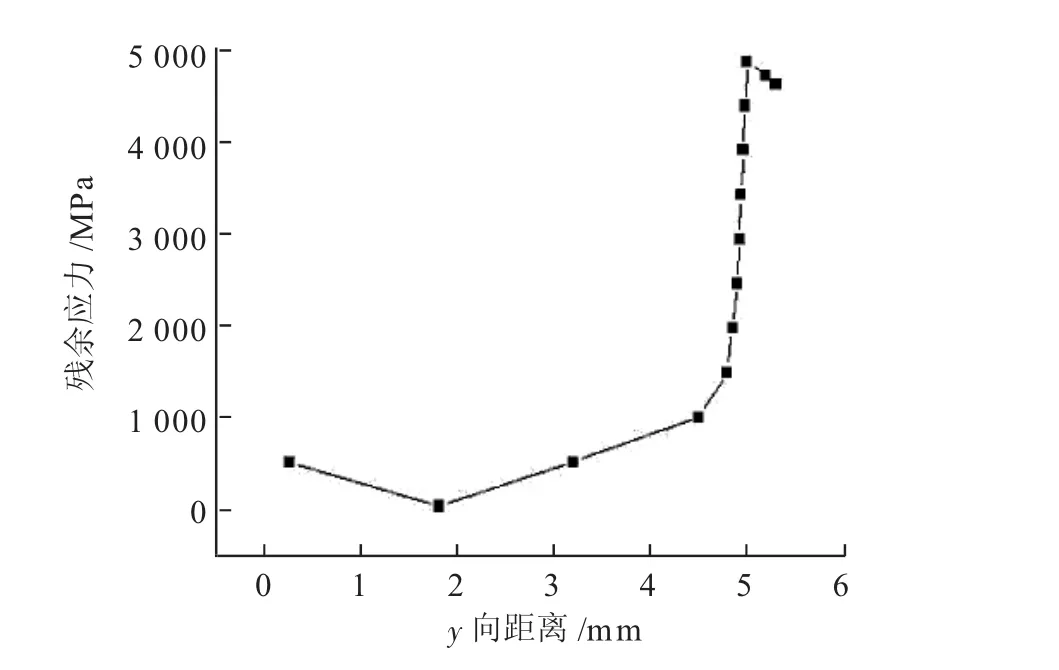
图2 无冲击力时AT涂层试样在x=2 mm路径上的等效应力

图3 有冲击力时AT涂层试样在x=2 mm路径上的等效应力

图4 无冲击力时AT涂层试样在y=5 mm路径上的等效应力

图5 有冲击力时AT涂层试样在y=5 mm路径上的等效应力
对比图2、图3可知,当考虑喷涂粒子冲击力时,试样内的残余应力的值增加了近2个数量级,应力分布趋势也明显改变:基体内的应力梯度增大,应力最大值由界面转移到了涂层表面,最小值位于基体内部。这是因为:喷涂粒子冲击力会使试样发生微量弯曲变形,中性面附近,变形最小,弯曲应力最小,离中性面越远,弯曲应力越大;弯曲应力与残余热应力相互叠加,形成图5所示的情况[5-6]。
对比图4、图5可知,不考虑喷涂粒子冲击应力时,等效残余应力最大值位于界面边缘处,最小值存在于距离x=6 mm处,靠近中心轴,应力分布均匀;考虑喷涂粒子冲击力时,等效残余应力最大值位于距离x=3 mm处,最小值位于界面边缘。二者分布趋势明显不同。
综上所述,喷涂粒子冲击力不仅使应力值发生明显变化,还会影响残余应力的分布趋势。因此在分析涂层失效原因时,不能忽略喷涂粒子的冲击力。
2.3 双层涂层残余应力的计算
当在陶瓷涂层和基体之间增加一层厚100 μm的镍包铝过渡层,从而形成双层涂层后,仍采用上述模型进行残余应力的计算。AT涂层添加过渡层后的应力计算结果见图6~8。

图6 AT涂层添加过渡层后在x=2 mm路径上的等效应力

图7 AT涂层添加过渡层后在y=5 mm路径上的等效应力

图8 AT涂层添加过渡层后在y=5.1mm路径上的等效应力
比较图6和图3可知,增加过渡层后,在相同的x=2 mm路径上,残余应力值明显降低,界面处应力突变程度也明显缓和。这是因为:过渡层物性参数介于基体和AT涂层之间,可明显缓和界面处物性突变,降低应力集中,进而使整体残余应力明显降低。
对比图7、图8可发现,二者应力分布趋势大致相同,只是后者应力值比前者稍大。这是因为:第一,过渡层与基体之间的物性参数差异,要比过渡层与涂层之间的物性参数差异小得多;第二,过渡层与涂层界面离涂层表面较近些,其弯曲应力较大些。
3 结论
通过以上对残余应力的计算和分析,得出以下结论:
(1)在只考虑温度因素时,基体内部残余应力分布均匀,且应力值很小,在基体与涂层界面上存在着一个很大的应力突变,并且界面处应力值很大。
(2)喷涂过程中的粒子冲击力,在涂层表面产生残余压应力,使试样的残余等效应力值增大了近2个数量级,其分布趋势也发生了显著变化,最大值由界面转移到了涂层表面,最小值位于基体中部,并且基体内应力梯度显著增大。
(3)在基体和陶瓷涂层之间添加过渡涂层而形成双层涂层后,可有效缓解界面处的应力突变。

