欧拉-拉格朗日法模拟桩靴插拔对邻近桩基承载力的影响
肖 辉,万 军,关 湃
中海石油(中国)有限公司天津分公司,天津 300459
自升式钻井船在执行钻井作业时,依靠其桩腿底部的大直径桩靴,贯入到泥面以下一定深度处来提供钻井工作时需要的承载力,当钻井作业结束后,再将已贯入的桩靴拔出,继续拖航至下一工作地点。自升式钻井船往往要在靠近海上固定平台处施工,大直径桩靴的贯入不可避免地对邻近平台基础产生不利影响,甚至危及平台的安全。因此,评价桩靴插拔对邻近桩基的影响,是保证桩靴贯入顺利进行的必要前提[1-4]。
已有大量学者研究了插拔效应导致的桩身位移和相应的弯矩和剪应力的变化。周龙[5]采用CEL方法研究了桩靴下沉速度对邻近桩基础的影响,发现无桩时,桩靴贯入速度对土阻力影响较小,土体的破坏和剪应力水平略有不同;桩靴的贯入速度对桩身的水平位移影响较小,但对桩身最大应力有较大影响。殷齐麟[6]以胜利9号平台在老174号井位插桩过程为例,基于RITSS大变形数值计算方法,研究了桩靴贯入过程土体变形和地基承载力随深度的变化规律,并且通过与SNAME规范对比,验证了RITSS方法研究桩靴在软硬相间地基上插拔的有效性。Khow[7]采用CEL方法分析了钻井船插拔对邻近桩基础弯矩影响,并且探讨了土体的弹性模量、桩身刚度、桩直径和桩头约束条件等因素对桩身弯矩分布的影响;Siciliano[8]针对单一黏土层开展了100 g(g为重力加速度)离心模型试验,研究了桩靴与桩基础间距对桩身位移和桩身弯矩的影响,发现桩身最大弯矩出现位置基本与桩靴贯入深度一致,且桩身弯矩随桩靴与桩间距的增大而减小。Xie[9]针对单一黏土情况和砂土层上覆黏土层情况,开展了离心模型试验,揭示了桩靴插深、桩靴尺寸、桩靴与桩间距和桩基形状和尺寸改变等情况下,桩身弯矩随桩靴插深的变化。吴永韧[10]针对饱和粉砂情况开展了1 g条件下的模型试验,研究发现砂土的密度、桩靴与桩间距和桩靴压入速度对桩头位移有明显影响,发现桩顶端位移随桩靴直径的增加而增加,随土体密度和桩靴与桩间距增加而减小。
综上所述,目前桩靴插拔对临近桩基影响的研究,主要集中在由挤土效应而导致的桩身变形和相应的弯矩分布,而对桩基的承载力影响研究内容较少。因此本文对动力算法计算单桩承载力的适用性进行了探究,并分析了在不同桩靴与桩间距情况下,桩靴插拔对邻近桩基承载力的影响规律。
1 欧拉-拉格朗日法
1.1 模拟方法概述
CEL(Coupled Eular-Lagrangian Technique)方法是耦合的欧拉-拉格朗日方法的简称,该方法结合了拉格朗日有限元与欧拉有限元的特点。拉格朗日有限元方法以物质坐标为自变量,把物体的变形和运动中的物质点的各个物理量,表示为物质坐标与时间函数,因此分析中有限元离散网格会随物体的形状变化而变化;欧拉有限元以空间坐标为自变量,把物体变形与运动中物质各点表示为空间坐标与时间的函数,因此计算中空间的网格形状、大小和位置保持不变,物质可以在网格之间流动。拉格朗日和欧拉有限元分析中连续体的变形如图1所示。

图1 有限元分析中连续体的变形
在CEL方法中,欧拉材料的体现是基于流体体积方法,即材料在网格中流动的轨迹是通过计算每一个单元中的欧拉体积分数(EVF)来确定。如果单元完全被材料填充,则EVF=1;如果单元没有材料,则EVF=0;如果某单元的EVF<1,则这个单元的剩余部分自动被空所占据,空材料即没有材料也没有强度。使用体积分数工具,在欧拉体中定义材料的过程如图2所示。
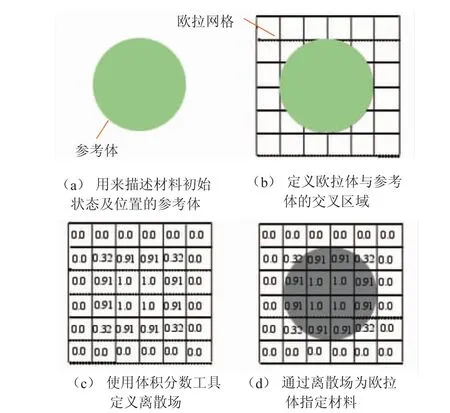
图2 使用体积分数工具在欧拉体中定义材料的过程
CEL方法将拉格朗日有限元与欧拉有限元有机结合,充分发挥了各自的优势,克服彼此的缺陷与不足,在解决物体大变形问题上具有独特优势。针对桩靴插拔对邻近桩基础的影响这一实际工程问题,利用CEL方法将桩靴插拔产生大变形区域设为欧拉体,采用欧拉有限元方法计算该区域的变形响应;桩基础所在区域设置为拉格朗日体,采用拉格朗日有限元计算变形响应。
1.2 计算模型
运用CEL有限元方法,建立了桩靴插拔对邻近桩靴影响的有限元计算模型,见图3。

图3 计算模型示意
计算模型中,整个土体设置为欧拉实体,采用六面体欧拉实体单元EC3D8R划分,土体本构关系选用摩尔-库伦弹塑性模型。将整个模型上部10 m范围内设置为空,为桩靴插拔过程中土体向上隆起变形提供空间;另外,桩底端部分土体设置为空,用于嵌放拉格朗日体,用于计算桩靴插拔过程对桩身变形的响应和承载力,拉格朗日体采用六面体拉格朗日实体单元C3D8R进行划分。
2 CEL法计算单桩承载力
分析了动力算法中加荷速度、网格尺寸、拉格朗日体范围等参数对桩基竖向承载力的影响;计算了不同土强度工况下桩的竖向承载力,并与API规范的计算值进行了对比。
2.1 网格划分
计算了三种网格尺寸条件下的桩基竖向承载力,网格尺寸分别为0.15 d(d为桩基的直径,m)、0.25 d、0.35 d。计算模型中:桩直径为1.2 m,桩长为60 m,桩长的30%嵌入拉格朗日土体中,桩的加荷速度为5 cm/s;土体为均质黏性土,强度为su=50 kPa,取弹性模量Es=50 MPa,泊松比v=0.49。计算结果如图4所示。

图4 网格尺寸对竖向承载力的影响
分析Q-s曲线可知,动力算法中,网格精度对单桩承载力有一定影响,随着网格精度的提高,桩基竖向承载力计算向真实值收敛。但是CEL的计算速度主要取决于稳定时间增量(stable time increment),而稳定时间增量主要与最小网格尺寸有关,考虑到计算时间成本,需要选取合适的网格尺寸。分析三个精度的网格尺寸:0.25 d的计算结果与0.35 d相比较为精确,而且计算成本远比0.15 d时低。因此,选择0.25 d的网格尺寸较为合适。
2.2 加荷速度
计算了三种加荷速度条件下的桩基竖向承载力,桩基础的加荷速度分别为3、5、10 cm/s。计算模型与上述研究网格尺寸的模型一致。计算结果如图5所示。
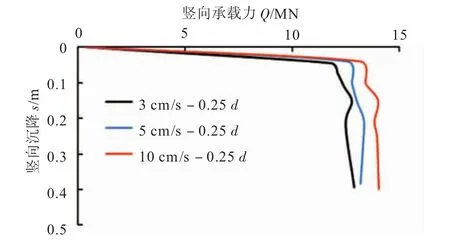
图5 加荷速度对竖向承载力的影响
分析Q-s曲线可知,动力算法中,加荷速度对桩的竖向承载力有一定影响,随加荷速度的增加,计算的承载力会随之增大。综合考虑计算成本及计算精度要求,选择5 cm/s的加荷速度较为合适。
2.3 拉格朗日体范围
计算了三种拉格朗日体深度情况下的桩基竖向承载力,桩基嵌放至拉格朗日体中的深度分别为桩长的10%、30%、50%。计算模型与Xie离心模型试验相一致,计算的桩长为27 m,桩径1.26 m,壁厚38 mm;计算土层为黏性土,深度为37 m,强度沿深度方向线性增加(顶面处强度为3 kPa,底面处强度为58 kPa),土弹性模量与强度比值为定值,Eu/su=150,下部有3 m的砂层。计算结果如图6所示。
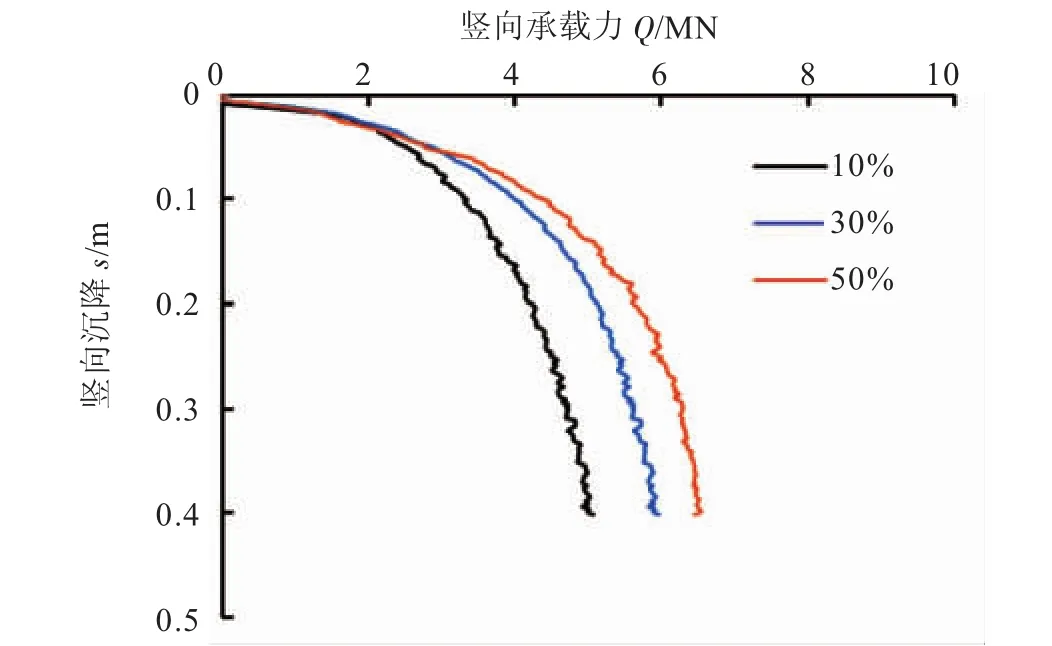
图6 网格精度对竖向承载力的影响
分析Q-s曲线可知,动力算法中,桩端嵌入至拉格朗日体的长度对竖向承载力有一定影响,随桩端嵌入至拉格朗日体中比例的增加,桩的承载力有增加的趋势,结合中桩身弯矩与离心模型试验对比,发现桩底端30%嵌入拉格朗日体中较为合适。
通过以上参数敏感性分析,确定了计算参数的取值:桩及桩周土体网格精度选用0.25 d,加荷速度为5 cm/s,拉格朗日体深度范围为:桩长的30%嵌放于拉格朗日土体中。使用动力算法计算了原型桩基承载力,并且与API规范[11]进行了比较,计算工况为桩长60 m、桩径1 219 mm,土强度分别为20、30、40、50 kPa,对比结果如表1所示。

表1 数值模拟结果与API计算值对比
采用上述确定的参数计算得到的桩基竖向承载力比API偏大在20%以内,且不同土强度计算结果具有一致性,因此使用动力算法计算单桩竖向承载力具有适用性。
3 桩靴插拔对邻近桩的影响分析
研究了桩靴贯入速度对桩身弯矩的影响,比较了不同桩靴与桩间距情况下,桩靴插拔后邻近桩基承载力的变化规律。
3.1 邻近桩桩身弯矩的变化
以Xie的100 g离心模型试验为依据,分析了数值模拟方法中,不同桩靴贯入速度对桩身弯矩的影响。Xie的离心模型试验共有三种工况,分别为NC1、CS1和CS2工况,如表2所示。试验中,桩靴直径D为15 m,桩长为27 m,桩径1.26 m,壁厚38 mm;黏土强度线性增长,强度沿深度方向线性增加,土弹性模量与强度比值Eu/su=150。数值模拟中,计算了NC1工况下,桩靴贯入后邻近桩身弯矩分布。桩靴贯入速度分别为1、6、8、10 m/s,桩身弯矩的分布如图7所示。

表2 离心模型试验工况
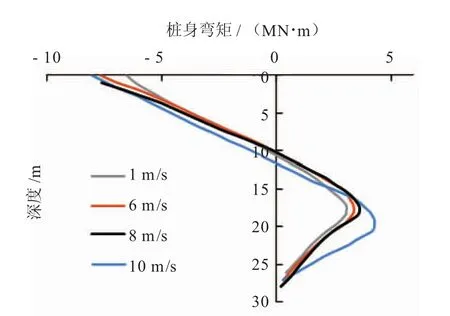
图7 NC1工况桩靴插拔速度对桩身弯矩影响
由弯矩对比可知,桩靴插拔速度对桩身弯矩分布有一定影响,随着桩靴插拔速度的增加,桩身最大弯矩呈增加趋势。
通过大量计算发现,桩长30%嵌固在拉格朗日体中、桩靴贯入速度为8 m/s时,桩身弯矩的数值模拟结果与离心试验结果吻合较好。图8~10为桩靴贯入15m时,数值模拟结果与离心模型试验结果的对比。

图8 NC1工况桩身弯矩对比
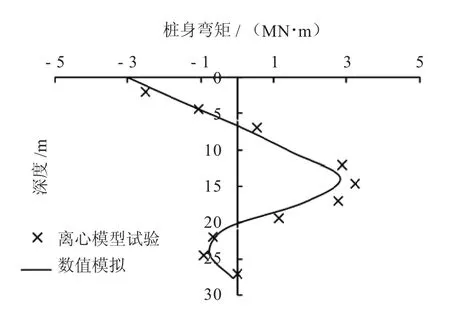
图9 CS1工况桩身弯矩对比
由图8~10可知,随着桩靴与桩间距的增加,桩靴贯入对桩身弯矩的影响呈减小趋势;桩身最大正弯矩位置与桩靴贯入深度基本相同;当桩底端嵌入砂土层中,桩底端处会出现负弯矩。
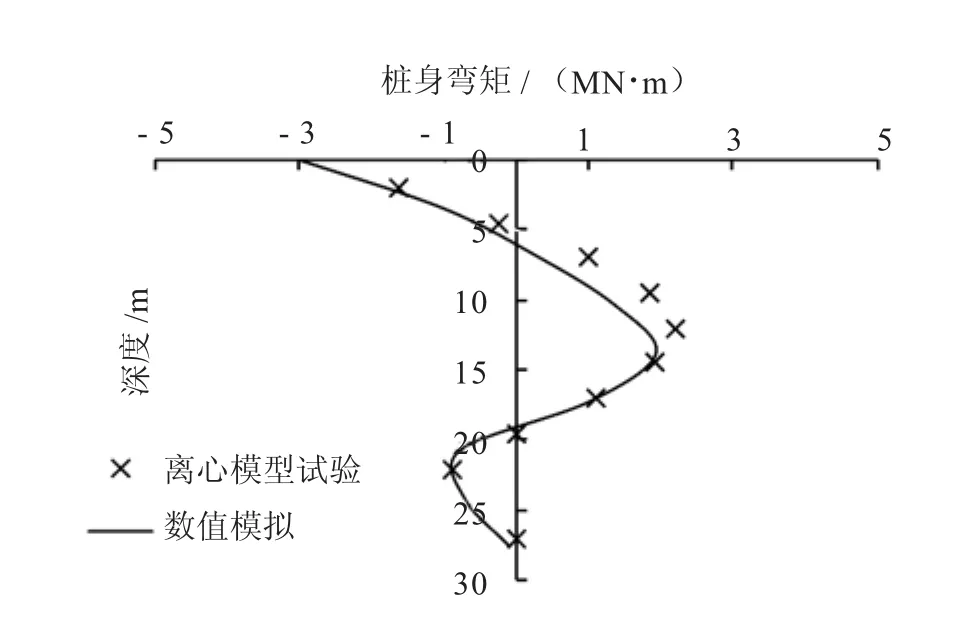
图10 CS2工况桩身弯矩对比
3.2 邻近桩承载力的变化
计算了桩靴插后邻近桩基竖向载力的变化情况,计算工况为:桩长60 m、桩径1 219 mm,土强度为50 kPa,桩靴直径12 m,桩靴插深9 m,桩靴与桩间距分别为0.25 D、0.5 D、1 D。桩靴插拔前后承载力变化如图11所示。

图11 桩靴插拔前后竖向承载力变化
从图11可以看出,桩靴插拔后,桩靴与桩间距为0.25 D的桩基的承载力下降约9%,间距0.5 D的桩基础承载力下降约8%,间距1 D的桩基承载力下降约5%;承载力下降的整体趋势随桩靴与桩间距的增大而减小,下降比在10%以内。
4 结论
研究了动力算法计算单桩竖向承载力的适用性,分析了桩靴插拔对邻近桩基的影响,具体结论如下:
(1)动力算法对计算单桩竖向承载力具有适用性;综合考虑计算成本与计算精度,确定了网格尺寸0.25 d,加荷速度5 cm/s,桩长30%嵌放至拉格朗日时能够较为准确地计算单桩竖向承载力。
(2)桩靴插拔速度对桩身弯矩分布有一定影响,随着桩靴插拔速度的增加,桩身最大弯矩呈增加趋势,当桩靴插拔速度为8 m/s时,桩身弯矩的计算值与Xie离心模型试验值吻合较好。
(3)桩靴插拔后邻近桩基竖向承载力会有一定程度下降,且下降比例随着桩靴与桩间距的增大呈减小趋势,下降比例在10%以内。

