基于混凝土双轴强度准则的重力坝可靠度分析

柯书武，于 强，柯济民

(1.江西丰饶工程监理有限公司，江西 上饶 334000；2.江西丰饶水利工程质量检测有限公司，江西 鹰潭 335000)

0 引 言

目前，国内外对重力坝的可靠度研究主要集中在建基面抗滑稳定等方面[1-6]，对基于不同强度准则的重力坝可靠度分析研究成果相对较少。混凝土强度准则有多种，包括垂直抗拉准则、单轴拉伸准则、双轴强度准则等。因为双轴强度准则考虑了第三主应力为压应力时对坝体开裂的产生的影响，因此采用双轴强度准则更加合理。本文采用线弹性有限元法对基于混凝土双轴强度准则的重力坝可靠度进行研究。

1 计算原理

1.1 混凝土双轴强度准则

我国混凝土结构设计规范GB50010-2010将混凝土的多轴强度在附录中专门列出。它规定，在双轴应力状态下，混凝土的设计强度值按图所示的包络图取值，在不同平面应力区的破坏包络线为多段折线，混凝土双轴强度包络图见图1。以应力比表示的极限状态方程分别为[7]：

(1)二轴压压：σ1=0，α1=f2/f3>0

当α1≥0.2时，

fc+f3/1.2=0，fc+f2/1.2α1=0

(1)

当α10.2时，

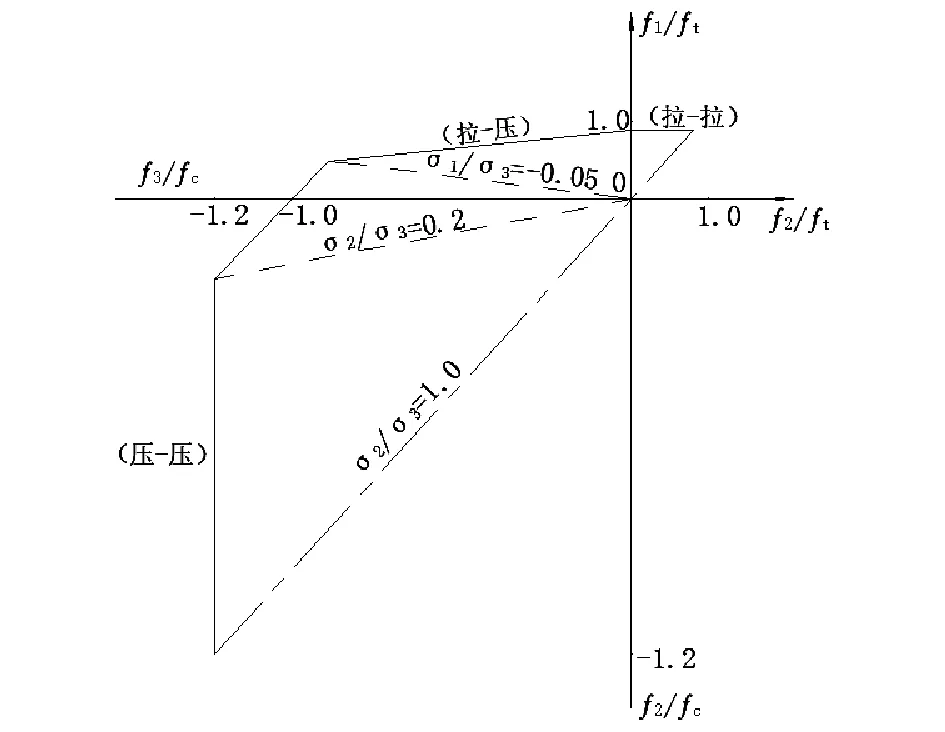
图1 混凝土双轴强度包络图

(2)

(2)二轴拉压：σ2=0，α2=f1/f3<0

当α2>-0.05时，

(3)

当α2<-0.05时，

(4)

(5)

(3)二轴拉拉：σ3=0，α3=f2/f1

ft-f1=0，ft-f2/α3=0

(6)

其中，fc，ft分别为混凝土单轴抗压和单轴抗拉强度设计值，f1，f2，f3的含义与σ1，σ2，σ3相同。

1.2 相应于某一功能函数的可靠指标计算公式

用广义随机空间内的可靠度分析方法计算出对应的可靠指标和设计验算点，其计算公式为[8]：

(7)

(8)

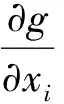
1.3 计算步骤

将有限元算法与上面的可靠度分析方法相结合，即可进行基于混凝土双轴强度准则的重力坝点可靠度分析。其具体过程为：

(1)在均值点处进行线弹性有限元分析；

(2)选定迭代初值x0=(μx1，μx2，…，μxn)；

(3)求非正态变量的正态当量均值μxi′和标准差σxi′；

(4)根据双轴强度准则公式求功能函数g(x)的值；

(5)根据式(8)求得新的验算点值x*；

(6)判别g(x)是否满足精度要求，若不满足则重复步骤(3)～(5)；

(7)根据式(7)求得可靠指标β；

(8)对单元和高斯点进行循环，求出单元的每个高斯点的可靠指标；

(9)对上述结果进行整理，求出所有结点的可靠指标。

2 实例分析

某混凝土重力坝，坝顶高程384.00 m，最大坝高162.00 m，坝顶长度896.26 m；左岸坝后厂房和右岸地下厂房各装4台800 MW 机组。

2.1 坝体剖面和有限元网格

对泄4坝段进行了精细模拟，考虑了中孔和表孔的影响，对地基进行了简化。其中主滑面与水平面夹角为26°，滑出面与水平面夹角为45°，计算剖面见图2。

根据计算要求，对泄4坝段建立了有限元模型，采用平面四节点等参单元进行离散。坐标系取为与坝体坐标一致，x轴沿顺河向，向下游为正，y轴为竖向，向上为正。坝基分别从坝踵和坝趾向上、下游延伸300.00 m，基础深度也取300.00 m。未考虑廊道的影响。坝基简化为均质坝基。其中溢流坝段考虑上部导墙结构宽度为6.00 m，中孔的宽度14.00 m，坝段宽度为20.00 m。采用广义接触面单元模拟建基面和深层滑动面。有限元网格离散为7 742个单元，7 963个节点，有限元网格见图3。

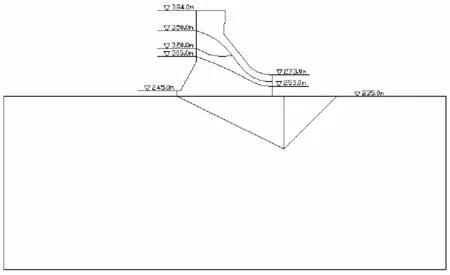
图2 坝体剖面图

图3 初始有限元网格

2.2 荷载

(1)自重：坝体容重24 kN/m3，基岩容重26 kN/m3。

(2)静水压力：上游水位380.00 m，下游水位265.80 m。

(3)扬压力：坝基面扬压力按考虑抽排降压效果计算。扬压力计算对应的排水孔位置及采用的系数见表1。

(4)淤沙压力：百年淤沙高程310.00 m，淤沙浮容重7.8 kN/m3，内摩擦角12°。

表1 泄4坝段排水孔位置与扬压力系数

2.3 力学参数与随机变量统计参数

泄4坝段各材料分区的物理力学参数标准值见表2，随机变量统计参数见表3。

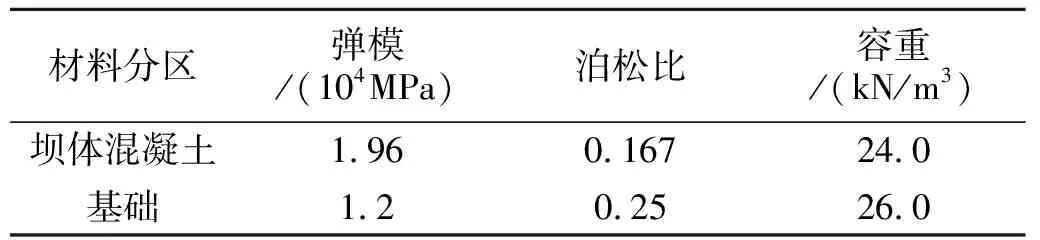
表2 泄4坝段各区材料主要物理力学参数标准值

注：基础简化为均质地基，材料参数取III1岩石对应的参数。

2.4 计算结果及分析

由图4可知，可靠指标最小值在坝踵附近，说明坝体最有可能破坏的地方在坝踵附近，这是因为坝踵处局部拉应力集中的缘故。在中孔和表孔附近，可靠指标也相对较小，这是因为泄水孔附近的坝体被削弱，应力状态比较复杂，设计与施工时也要重点关注。

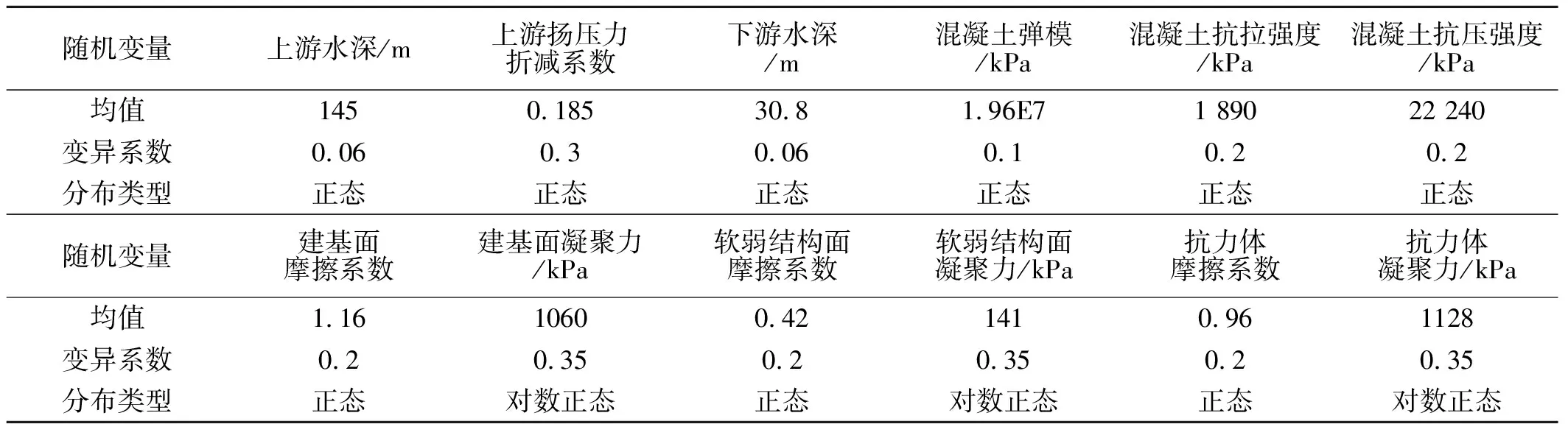
表3 泄4坝段随机变量统计参数表

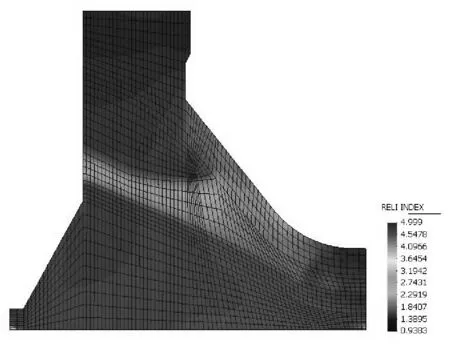
图4 双轴强度准则对应的坝体可靠指标

3 结 语

(1)采用线弹性有限元法和广义随机空间内的可靠度分析方法，对基于混凝土双轴强度准则的某重力坝可靠度进行了分析，得到了坝体不同部位的点可靠指标。

(2)采用有限元法计算重力坝的可靠指标，可以考虑孔口和坝体局部应力集中以及地基的影响，结果与实际情况相符。