Spatial Pattern Induced by Cross-Diffusion in a Chemostat Model with Maintenance Energy
LIU Qingsheng (), PENG Yahong()
College of Science, Donghua University, Shanghai 201620, China
Abstract: A chemostat model with maintenance energy and cross-diffusion is considered, and the formation of patterns is caused by the cross-diffusion. First, through linear stability analysis, the necessary conditions for the formation of the spatial patterns are given. Then numerical simulations by changing the values of cross-diffusions in the unstable domain are performed. The results show that the cross-diffusion coefficient plays an important role in the formation of the pattern, and the different values of the cross-diffusion coefficients may lead to different types of pattern formation.
Key words: pattern formation; chemostat model; cross-diffusion; Turing instability; stability
Introduction
The chemostat model is one of the most significant models in mathematical biology and it has been widely applied to the study of population growth and interaction of microorganisms by researchers[1-3]. It is known that the microbe may be able to recognize the nutrient so that microbes would gather to high concentrations of nutrient[4-7]. In addition, with the flow of fluid, concentrations of microorganism and nutrient also may change. This phenomenon is called cross-diffusion. Recently, researchers are paying great attention to the study of self-diffusion and cross-diffusion effects on biological models, such as Refs.[8-10]. More recently, Zhangetal.[11]considered the following spatially generalized version of chemostat model
(1)
where,the equations have been rescaled to a dimensionless form;uandvrepresent concentrations of nutrients and microorganisms at timet,respectively. All parameters are positive and 0≤β≤1. For a detailed explanation of the parameters, please refer to Ref. [11] and references there.d11>0 andd22>0 are self-diffusion coefficients, which denote respective population fluxes of nutrients and microorganism.
As shown in formula(1) in Ref. [11],the model only has the self-diffusion terms and subject to a homogeneous Neumann boundary condition. They proved that the constant steady state is globally asymptotically stable when it exists. It means that it is impossible to have any spatial patterns. Based on the work of Ref. [11], we now study the effect of cross-diffusion on the dynamics of the following chemostat model, which is a generalization of system (1).
(2)
whered12andd21are cross-diffusion coefficients, which describe the respective population fluxes of nutrient and microorganisms in the case of the flow of fluid. The cross-diffusion coefficientd12represents the effect of microbial concentration to nutrient concentration. Ifd12>0, it means that nutrients is repelled from microorganisms; and ifd12<0, it means that nutrients is attracted to microorganisms.d21has the same meaning with regard to the role of nutrients and microorganisms switched. In this paper we only consider thatd12andd21are all positive for convenience.
In order to compare with the work of Ref. [11], we also assume that β=0. Then system (2) can be concisely written as
(3)
under the following initial condition and homogenous Neumann boundary condition:
u(x,y, 0)=u0(x,y)>0,
v(x,y, 0)=v0(x,y)>0,(x,y)∈Ω,
(4)
(5)
Our main concern is whether the cross-diffusion can result in pattern formation from the above system. The rest of this paper is organized as follows. We first theoretically analyze the emergence of pattern induced by cross-diffusion and then give necessary conditions for pattern formation in section 1. Then we perform numerical simulations by changing the values of cross-diffusion coefficientd21in Turing unstable domain in section 2. The result shows that there will be different types of patterns. Finally, a brief summary is given in section 3.
1 Turing Instability
It is easy to find that system consisting of formulas (3)-(5) has two equilibrium points: a washout equilibriumE0=(s0,0) and a positive equilibriumE*=(u*,v*)with
provided the condition
holds.
Whendij=0(i,j=1,2),namely without diffusive effect, the Jacobian matrix at the positive equilibriumE*is given by
(6)
where

Similar to Ref. [12], system (3) around the homogeneous steady stateE*is perturbed as follows.

λ2-Tkλ+Dk=0,k≥0,
(7)
where
Tk= -(d11+d22)k2+T0,
Dk=(d11d22-d12d21)k4-
(a11d22-a12d21-a21d12)k2+D0,
with
T0=a11+a22=a11,D0=a11a22-a12a21=-a12a21.

Lemma1(Ref.[11], Theorem 3.2) The positive equilibriumE*of system (3) withd12=d21=0 is globally asymptotically stable when the condition (C0) holds.
But when the cross-diffusion is present, namelyd12>0 andd21>0 in formula (3), the above result may not be true under the same condition (C0).
We also assume
(C1):d11d22>d12d21,
so that cross-diffusion is not overpowering self-diffusion.
Under the condition (C1),Tk<0 for anyk, while the expressions ofDkimply that there must exist someksuch thatDk<0, which is caused by cross-diffusiond21. This means that the appearance of cross-diffusion term destroys stability. The Turing bifurcation occurs when
Re(λk)=0, Im(λk)=0, atk=kT≠0.
And the wave numberkTsatisfies

(8)
By further analysis, we know that the appropriate cross-diffusion could cause instability. The necessary conditions of Turing instability are given as follows.

and

Obviously, if condition (C3) holds, then the condition (C2) also holds. According to the above discussion, we summarize the following theorem.
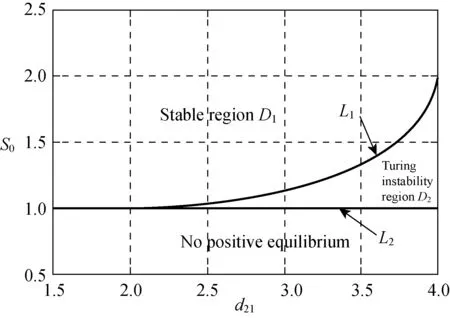
Fig.1 Bifurcation diagram for system (3) with d11=4; d22=d12=2; τ=1, kd=ms=0.5
2 Simulation of Pattern
The theoretical analysis in section 1 shows that the cross-diffusion termd21causes Turing instability. So in this section, we perform numerical simulation in the regionD2in Fig.1 by changing the values ofd21and exhibit different types of pattern of system (3). Our simulations are all based on the Neumann boundary and non-zero initial condition. Additionally, we only show our result of pattern formation for nutrients since the microorganisms are always of the similar type.




Fig.2 Numerical simulation for stable spotted patterns of nutrients (snapshots of contour pictures of the time evolution at different instants with d11=4, d22=d12=2,d21=2.950 18, τ=1, kd=ms=0.5, s0=1: (a) 3 000 iterations; (b) 300 000 iterations; (c) 510 000 iterations)
In Fig.2, we selectd21=2.95 018 in the vicinity of the Turing branch of the unstable region to perform numerical simulation. In the results, we select the three images with the largest variation of type, at 3 000, 300 000, 510 000 iterations. Figures 2(a)-2(c) show the forming process of spot pattern. This phenomenon comes into being slowly, and settles down in the end Fig.2(c).
Figure 3 shows the snapshots of spatial pattern of nutrients whend21=3.05 at 3 000, 200 000, 310 000 iterations. Figures 3(a)-3(c) show the change from the spot pattern to spots-stripes, and Fig.3(b) show a competition between spot pattern and stripes pattern.
Figure 4 shows the evolution of Turing pattern of nutrients whend21=3.4 at 5 000, 80 000, 200 000 iterations. Figures 4(a)-4(c) show the change from the spots-stripes to stripes pattern, and Fig.4(b) shows a phenomenon which some points gradually began to gather to form a strip.



Fig.3 Numerical simulation for coexistence of stable spotted patterns and stripe patterns of nutrients (snapshots of contour pictures of the time evolution at different instants withd11=4, d22=2, d12=2, d21=3.05, τ=1, kd=0.5, ms=0.5, s0=1.1; (a) 3 000 iterations; (b) 200 000 iterations; (c) 310 000 iterations)



Fig.4 Numerical simulation for stable stripe patterns of nutrients(snapshots of contour pictures of the time evolution at different instants with d11=4, d22=d12=2, d21=3.4, τ=1, kd=0.5, ms=0.5, s0=1.1: (a) 50 000 iterations; (b) 80 000 iterations; (c) 200 000 iterations)
3 Conclusions
In this paper, we study the chemostat model with cross diffusion by linear analysis. Through theoretical analysis, we give the necessary conditions for the formation of the pattern caused by cross-diffusion. In order to support our theoretical findings, we validate our conclusions by numerical simulation. We choose different values ofd21inD2of Fig.1, and obtain three categories patterns: spot pattern (Fig.2(c)), spot-stripe pattern (Fig.3(c)) and stripe pattern (Fig.4(c)). Both theoretical analysis and numerical simulation show that cross-diffusion plays an important role in the formation of the pattern.
 Journal of Donghua University(English Edition)2018年6期
Journal of Donghua University(English Edition)2018年6期
- Journal of Donghua University(English Edition)的其它文章
- Stochastic Stabilization for Nonhomogeneous Markovian Jump Discrete-Time Singular Systems
- Structural Reliability Analysis and Design Optimization of Hot-Rolled H-beam Steel Universal Mill
- Improved Composite Nonlinear Feedback Control for Robot Manipulators
- Zeta Functions of the Complement and xyz-Transformations of a Regular Graph
- Kenyan Wool Fiber Properties Sampled from Different Sheep Body Parts
- Variational Methods to Nonlinear Differential Equations with Non-instantaneous Impulses
