应用数学专业概率论实验课程的教学设计与思考
樊亚莉
(上海理工大学 理学院,上海 200093)
随着我国经济的快速发展,对应用数学专业的人才需求和要求亦有显著提升。越来越多的实际工作岗位不仅要求应用数学专业的人才具有较强的逻辑思维和抽象思维能力,更需要具有较强的创新能力和综合应用能力。概率论作为应用数学专业的核心课程之一,是专门研究客观世界中随机现象的数学分支课程,其突出特点是既有严密的数学基础,又广泛应用于自然社会人文等众多领域,与众多学科具有密切联系。因此概率论课程在培养学生理论联系实际和创新创造能力等方面,起着非常重要的作用。
但是,笔者在多年的本科教学过程中感到,目前应用数学专业的教学,普遍存在偏理论轻应用的现象,学生往往分析解决实际问题能力不高,创新创造意识不强。这使得我们培养的应用数学专业人才很难满足当前经济市场的需求。造成这种现象的原因涉及到教学方法、教学观念和成绩评价体系等多方面因素。就概率论课程而言,传统的教学方法往往偏重理论推理、公式运用以及计算解题等方面,而忽视对概率论在实际问题的应用方面的介绍和训练,这就使得学生对概率论中众多思想方法,如大数定律、中心极限定理等,缺乏深刻理解,也难以运用到实际问题中。同时,偏重理论的教学方法也容易使学生失去对概率论的学习兴趣。笔者的这些发现与参考文献[2-4]中的观点基本一致。
概率论课程紧密联系实践的特点决定了在教学过程中开设实验课的可行性,受到参考文献[5]和[6]中递进式教学方法的启发,本文希望通过对概率轮课程中实验课的设计,来辅助理论教学,将教学过程中难以理解的内容转化为直观的、易于理解的内容。学生通过简单易学的数学软件,自己设置参数并完成实验,从而深刻领会概率论的基本思想,逐步提高实践能力。
一、实验课程教学设计
(一)实验课程教学目的
熟练掌握几种常见离散型和连续型分布的相关函数命令,包括对应分布的随机数产生、分布函数、密度函数、分位数函数等命令;熟练掌握常用的特征数字的函数命令,例如均值、方差、中位数、协方差、相关系数、变异系数、峰度系数、偏度系数等;掌握常见的作图方法,包括绘制分布函数、密度函数、直方图等;能编写简单的程序来验证大数定律和中心极限定理;能设计简单的蒙特卡洛试验,来估计感兴趣的数值。
(二)软件介绍
由于实验课程中的案例的实现需要数学软件的辅助才能完成,因此在实验课程实现之前,需要学生熟悉一个合适的软件。目前数学和统计软件很多,比如功能强大的综合性软件MATLAB,统计学专业软件SPSS、SAS等。对于专业性较强的软件,往往需要专门的课程来学习。对于概率论这门独立课程,显然没有太多的课时用于软件学习,因此作为教学辅助,一款简单易学且容易配置的软件才能满足要求。R软件正是这样一款符合要求的软件。首先,R软件是一个开源项目,在很多操作系统上都可以免费安装;其次,R软件功能强大,基本安装就涵盖了数以百计的概率统计函数和图形函数;最后,R的最大优点在于可读性强,简单易学,学生往往只需要1课时就可以掌握R的基本操作。基于上述原因,本文接下来的案例设计都是基于R软件进行的。
(三)实验课教学内容
以56课时的应用数学专业的概率论课程为例,设计了8课时的实验课程。
1.重要的概率分布
计划用3课时使学生深刻理解重要分布的分布特点,参数含义以及密度函数的图形特征。重要的概率分布有:二项分布B(n,p)、泊松分布P(λ)、几何分布G(p)、均匀分布U(a,b)、指数分布Exp(λ)、正态分布N(μ,σ2)等。
实验Ⅰ内容如下:
(1)给定参数,绘制上述6种常见概率分布的密度函数和分布函数图,理解参数的大小变化对分布的影响;
(2)给定参数,计算常见概率分布的中位数,并与对应的数学期望进行比较;
(3)给定参数,考察运用泊松定理和中心极限定理对于二项分布下概率计算的近似程度。例如设随机变量X服从二项分布B(1 000,0.006),则计算概率随机变量X取值不超过8的概率的精确值,并利用泊松定理和中心极限定理分别计算其近似值,并加以比较。
实验Ⅰ的设计意图如下:
(1)希望学生通过实验理解常见分布的特点。比如通过更改参数λ的大小,可以发现,随着参数λ的增加,泊松分布的密度函数峰值向右偏移,而且泊松分布总是在参数λ附近取得较大概率值,而在距离λ较远处,概率值迅速向零衰减。又如对于正态分布,当参数μ固定时,改变σ的大小,分布的密度函数的陡峭程度发生改变,σ越小,分布越陡峭,而当参数σ固定时,改变μ的大小,分布的密度函数会左右平移,这样可以帮助学生理解μ为位置参数,而σ是形状参数。以正态分布N(0,1)为例,绘制密度函数和分布函数图在R中可以用命令
x<-pretty(c(-3,3),50);y<-dnorm(x,mean=0,sd=1);
z<-pnorm(x,mean=0,sd=1)
plot(x,y,type=″l″,xlab=″x″,ylab=″f(x)″)
plot(x,y,type=″l″,xlab=″x″,ylab=″F(x)″)
这里,用f(x)表示密度函数,用F(x)表示分布函数。
(2)希望学生理解各种常见分布与正态分布比较时的偏度。由于当分布右偏时,中位数小于分布的期望值,当分布左偏时,中位数大于分布的期望值,因此通过比较中位数和期望,可以理解该分布的偏度。以指数分布Exp(0.2)为例,通过命令qexp(0.5,0.2)可以算出指数分布Exp(0.2)的中位数为3.465 736,而期望值为5,因此推出指数分布的分布形状是右偏的。
(3)希望学生理解并运用泊松定理和中心极限定理求二项分布概率的近似值。在上述例子中,可以用命令pbinom(8,1 000,0.006)算出概率P{X≤8}的精确值为0.847 859 7,用命令ppois(8,6)和pnorm(8,6,sqrt(6×0.994))可分别算出泊松近似值为0.847 237 5,正态近似值为0.793 594 6,可见泊松近似较好。
2.蒲丰投针问题
用1课时完成蒲丰投针的模拟实验,要求学生根据课本上讲过的蒲丰投针问题设计一个蒙特卡洛实验,并在具体参数值下估算圆周率π的值。
实验Ⅱ内容如下:
假设平面上有间隔为d的等距平行线,向平面随机投掷一根长度为l的针(l 该实验可以在R中用以下命令来实现 A=NULL;n=10 000;d=1;l=0.8; for(iin1∶200){x=runif(n,0,d/2); y=runif(n,0,pi); F=(x<=(l/2)×(siny));F=as.numeric(F); A[i]=mean(F);mean(A)} 2×l/mean(A) 这里,设定平行线距离为1,针长为0.8,重复200次,用上述命令可以求得π的近似值为3.141 816,学生也可以采用其他参数设置。 该实验的设计意图是希望学生深刻理解几何概率的原理方法,并理解蒙特卡洛实验的作用,为后续的数学建模和本科毕业设计打下良好基础。 3.大数定律 用3课时完成实验Ⅲ。该实验的设计主要参考文献[1],目的是希望学生深刻理解大数定律的含义,同时通过概率实验来求出一些复杂积分的近似值。 实验Ⅲ内容如下: 实验Ⅲ的设计思路如下: 一般情况下,要求函数f(x)在区间[0,1]上的定积分,如果该函数的取值介于0和1之间,则可以把该积分值看成一个概率值。事实上,设二维随机变量(X,Y)服从矩形{0≤x≤1,0≤y≤1}上的均匀分布,则可求得边际分布分别为区间[0,1]上的均匀分布,则函数f(x)在区间[0,1]上的定积分等价于随机变量Y的取值不超过f(X)的概率,因此可以用频率来估计这个概率值。根据伯努力大数定律,随着做实验的总数n趋于无穷大,频率可以依概率收敛到概率。对于一般的复杂积分,如函数g(x)在区间[a,b]上的定积分,可以做一个变换,把它变为上述第一类积分。另外,也可以从另一个概率论角度来看待,由于假设X服从[0,1]上的均匀分布,可以把函数f(x)在区间[0,1]上的定积分看作函数f(x)的数学期望,然后可以根据辛钦大数定律,用平均值估计期望值的方法来求改积分的近似值。同样对于一般的积分,可以通过变量变换变为上述第一类积分。 以积分Ⅰ为例,可以通过以下命令来求该积分的近似值 A=NULL;n=10 000; for(iin1∶200){x=runif(n,0,1);y=runif(n,0,1); F=(y<=sinx×cosx×exp(-(x^2)/2)); F=as.numeric(F); A[i]=mean(F)};mean(A) 这个程序运行之后,得到积分Ⅰ约等于0.288 118 5。该实验也可以使用以下程序 A=NULL;n=10 000; for(iin1∶200){x=runif(1,0,1);A[i]=sinx×cosx×exp(-(x^2)/2)} mean(A) 上述程序运行一次之后可以得到积分Ⅰ约等于0.280 482 3,两种模拟给出的近似值接近,因此可以推断积分积分Ⅰ的值介于0.28到0.29之间。 4.中心极限定理 用1课时完成下列实验Ⅳ。该实验的设计目的是希望学生通过蒙特卡洛实验来验证并深刻理解中心极限定理。 实验Ⅳ内容如下: 实验Ⅳ中的参数可以改变,比如可以把随机变量序列的共同分布改为参数为0.3的指数分布,同时修改相应的Yn的表达式即可。中心极限定理所描述的结论正是,无论随机变量序列服从什么分布,只要满足独立同分布,那么随着n趋于无穷大,独立和的标准化变量都趋于标准正态分布。对于上述实验,可以通过以下程序实现。 A=NULL;n=10 000; for(iin1∶2 000){x=runif(n,0,1);y=(sum(x)-n×0.5)/sqrt(n/12);A[i]=y} hist(A) 运行该程序一次,可以得到以下直方图,如图1所示。 可以看到,模拟出来的Yn近似服从标准正态分布。 这里需要说明的是,上述实验Ⅱ、实验Ⅲ、实验Ⅳ的结果都依赖于所产生的随机数,如果没有固定随机种子,那么每次运行相同的实验产生的随机数虽然分布相同,但具体数值不尽相同,因此每一位同学所得到的结果不完全相同。学生正是在这种对随机性和规律性的不断观察中可以深刻理解概率论中有关随机性的基本概念。 图1 实验Ⅳ产生的直方图示例Fig.1 Sample histogram in experiment Ⅳ 针对应用数学专业本科生,采用紧密联系实际的问题设计了8课时的概率论实验课程。实验课和理论课相辅相成,互相促进。学生通过对实验课的学习,能引起对理论学习的兴趣,加深对理论学习的理解,增强学生学习的信心,同时理论学习也对学生实验课程具有指导意义。在理论教学中增设实验课的教学方式是实现学生自主学习的有效途径,能够促进学生养成对问题进行深入研究和思考的良好习惯。在应用型本科教学要求和大数据时代背景下,概率论实验课作为概率论理论知识和实际问题应用的桥梁,对培养学生的创新意识和创造精神起到十分积极的作用。
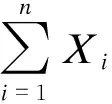
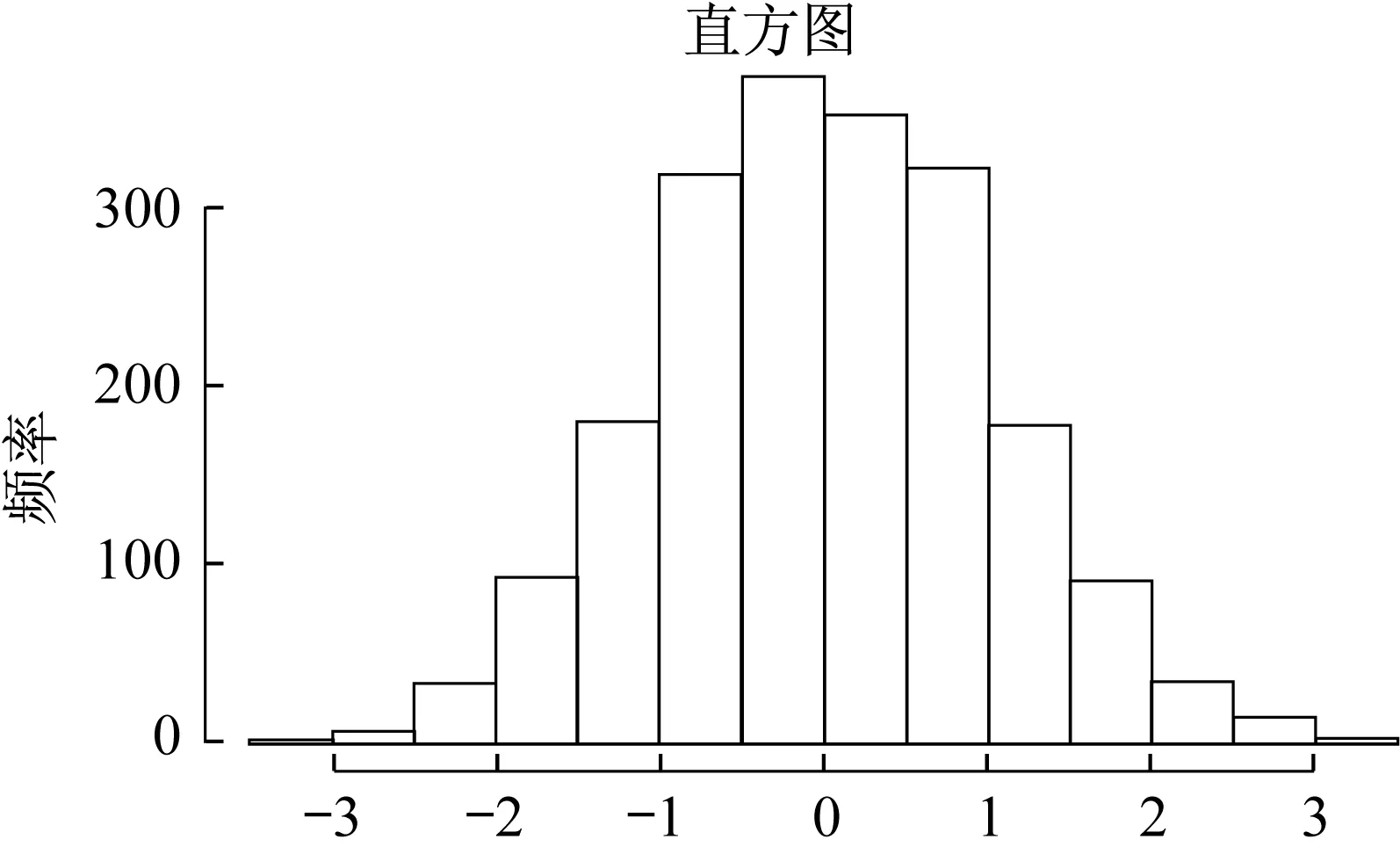
二、结束语

