利用Alpha-shape算法进行树冠三维模型构建

李 庆，高祥伟,费鲜芸，张 红，王 健，崔云健，李 彬

(淮海工学院测绘与海洋信息学院，江苏 连云港 222002)

树冠是森林生态系统的基本构成，树冠结构(如体积、表面积、疏密度、分枝特性)与树木光合作用潜力密切相关，是指示树木生长状况的重要指标[1-3]。三维激光扫描技术作为一种新型的测绘技术，能够高精度采集树木的三维点云数据，为树冠三维模型构建及林分结构计算提供有力的支持。但是由于树冠内部存在大量不规则空洞，以及树枝的相互遮挡，利用三维激光点云数据进行树冠三维建模、树冠内部结构参数计算尚存在难点[4-6]。

目前可用于计算树冠体积的三维模型主要有两种：①几何模型。戴超[7]利用快包法构建树冠点云的最外凸包模型；熊妮娜等[8-11]先后将树冠模拟为圆锥、圆台等规则几何体或不规则台体的叠加。这些几何模型主要以计算树冠外包体积为主，树冠点云内部的无效容积无法消除，对于冠层内部疏密、分枝特征表现不足，计算得到的结构参数也较单一，无法全面地指示树木冠层内部形态。②体素模型。吴宾等[12-13]先后建立体素模型，将待测空间分割为体素，包含激光点的有效体素个数乘以体素体积即得总体积。这种模型在树冠枝叶茂密时易受内部点云缺失影响，模型易形成内部空洞，也无法全面地指示树木冠层内部形态。

alpha-shape算法由Edelsbrunner[14-15]首先提出，最初用于点集轮廓的构建。目前该算法已被应用于网格生成、医学图像分析和可视化的地震数据结构等，也被应用于建筑物顶面轮廓的边缘提取[16-17]，但如何利用alpha-shape算法提取树冠散乱点云轮廓，进行树冠三维模型构建还缺少深入系统的研究。

本文将alpha-shape算法应用于复杂树木的模型重建，并通过对参数α大小的控制，对树冠进行三维模型重建；分析不同参数α时，所构建树冠三维模型的空间指示特征为树冠内部结构参数的计算准备基础。

1 树种选择

榉树在连云港市属于乡土绿化树种，被广泛用于城市绿化建设，在连云港城市绿化树种中具有代表性，在淮海工学院校内也作为重要的绿化树种广泛种植。目前校园内生长有不同树龄、不同胸径的榉树，为研究提供了丰富的可选样本。

本次研究选取连云港市淮海工学院校内20棵榉树为样本，数据测量信息见表1。为了减少叶片对树木内部遮挡而造成的点云缺失的影响，本研究选择在冬季树木落叶时进行扫描测量。

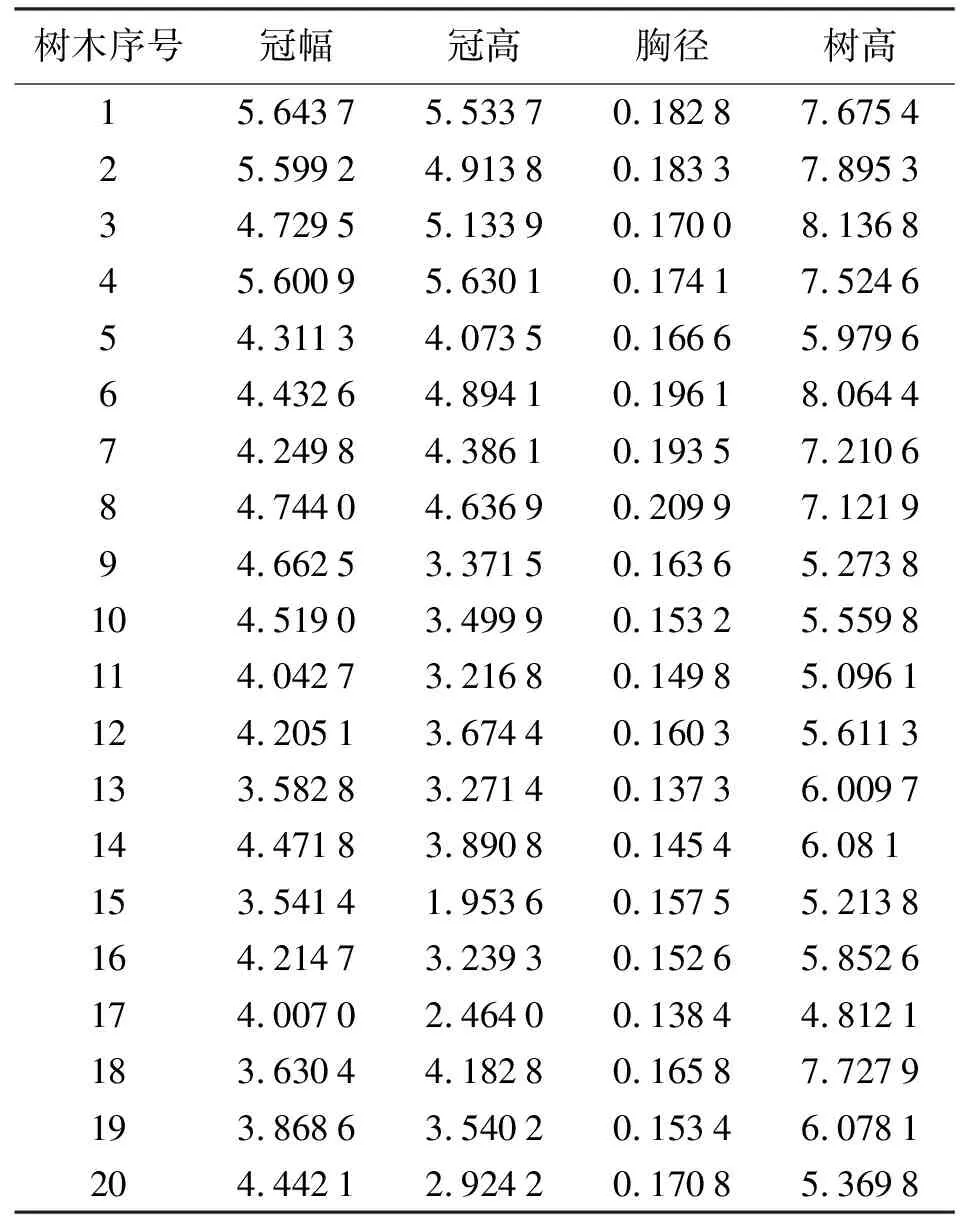
表1 样本数据统计指标 m

2 研究方法

2.1 数据采集与预处理

本文以徕卡ScanStation C10三维激光扫描仪作为数据获取平台，采用基于标靶的方法采集中等分辨率的点云数据，并利用Cyclone软件实现数据配准和去噪处理。以一棵树为例，样本的真实照片和预处理后的榉树点云数据如图1所示。

2.2 alpha-shape算法及其参数α

alpha-shape算法适合从一堆无序的点集中提取物体的边缘。算法原理如下：假设有一点集P，其alpha-shape是一个由点集P和半径参数α决定的唯一多边形。如图2所示，可设想成存在一个半径为α的圆，从点集P外某一点开始滚动，若α足够大，那么这个圆就不会滚到点集P的内部，则这个圆滚动的痕迹就是点集P的边界线。若α很大(α→∞)时，则检测出的边界线是点集P的凸包。同理，三维空间的alpha-shape算法则是通过三点作半径为α的球来判断边界点，并在得到的边界点处建立三角片面，重构出曲面。alpha值的设定直接影响三角形表面的重建结果，参数α控制了多面体生成的精细程度[18]。

图2 alpha-shape算法示意图

本文在Matlab环境下，利用alpha-shape算法，通过不断调整α参数的取值，对20棵样本榉树进行三维建模。根据试验效果，以α值选取0.01、0.02、0.03、0.04、0.05、0.06、0.07、0.08、0.09、0.1、0.25、0.5、1、10为例进行说明，通过三级树木枝条建模效果、树冠体积变化特征对运算结果进行分析评价。

3 结果分析

3.1 不同α参数树冠三维建模目视分析

以参数α分别取10、0.1、0.05、0.02及0.01时为例，对基于alpha-shape算法构建的三维模型进行目视分析，图3为树木冠体以及主枝、细枝的正视建模效果。

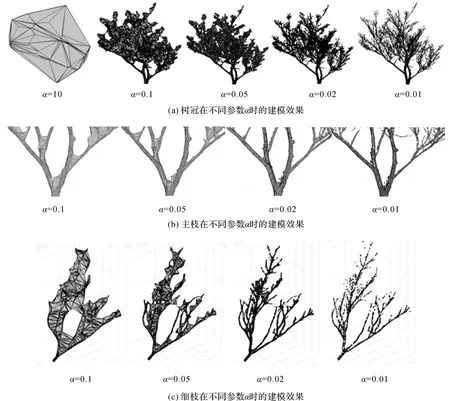
图3 三维模型效果

从图3可以看出，当参数α=10时，树冠结构被高度综合，生成的模型是最外部点云构成的凸包，此时模型对树冠内部结构无法表达，树枝无法重建；当α=0.1时，模型可以较好地表示树木冠层的凹凸不平曲面；当α=0.05时，曲面重建效果较差；当α=0.02时，三维结构其重建结果较为精细，树冠的几何结构和拓扑结构表达效果较好，树木主枝及细小枝条曲面重建效果较好，可以获取较精细的三维模型；但是当α取值过小时，如α=0.01，不能找到足够的点来组建曲面，因此得到的图形是一些离散的面片，重建结果不完整，会出现较多的孔洞。

通过调整α值，构建出的模型能够反映树冠在空间伸展时不同的形态、表面积、分枝特性、疏密程度等特征。因此，利用alpha-shape算法对树冠进行三维重建时，利用不同的参数α可以构建出树冠不同的空间形态特征。

3.2 不同α参数树冠体积分析

3.2.1 常用算法及不同α参数求得的树冠体积

由于目前树冠体积的真值无法获取，本文将取不同参数α值时样本树冠体积计算结果与快包法[7]计算结果进行对比，分析α值对树冠模型重建的影响。计算结果见表2，同时，分别计算alpha-shape算法不同参数α时的树冠体积与快包算法所得体积的相对差值均值及相关系数。

从表2可以看出，当α=10时，两种方法计算的树冠体积值趋于相等，树冠体积的alpha-shape算法与快包法算得的树冠体积平均相对误差为0.007，二者的相关系数高达1。而随着α的减小，alpha-shape算法获得的树冠三维模型包含的树冠孔隙越来越多，求得的体积也逐渐减少，两者的差值越来越大；相关性越来越小，当α=0.02时，平均相对误差值可达0.995，二者的相关系数只有0.101，也进一步说明精细模型能够较好地构建树冠内部结构，由于内部分枝特性不同，相同的外包模型内部结构差异较大。

3.2.2 树冠体积与树木物理参数相关性分析

将不同α参数下求得的树冠体积与冠幅、冠高、胸径进行相关性分析，统计结果见表3。

由表3可见，当α=10时，最外层树枝点云包围形成的体积不能反映树冠结凹凸不平，但可以反映整个树冠在空间的伸展形态，此时求得的树冠体积与冠幅、冠高相关性明显。随着α的减小，由于树冠三维模型逐渐接近树冠真实形状，不同的树木之间树冠结构差异对体积计算影响也越来越大，因此树冠体积与冠幅、冠高相关性逐渐减少。当α=0.02时，得到的树冠三维模型较精细，受内部结构变化的影响，此时二者在样本间已没有相关性。

还可以看出，胸径与树冠的三维体积的相关性明显区别于冠幅和冠高，不同参数α的树冠体积与胸径相关系数都较大(0.01时除外，此时构建的三维模型较离散，结构不完整)，而且该相关性在α=0.1时达到最大，此时的冠体模型由树冠的凹凸表面构成。

取不同参数α时构建的树木三维模型反映了树冠的不同空间形态特征，进而可用于指示树冠参数的研究，而相关参数的指示意义需要进一步量化和分析，受论文篇幅的影响，相关研究需要在以后的研究中详细开展。

4 结 语

本文利用alpha-shape算法对榉树激光扫描点云数据进行三维建模，并对不同参数构建的树冠三维模型进行分析，可以得出：

参数α=10时，构建的三维模型较综合，可以反映整个树冠在空间的伸展形态，形状较稳定，但树冠内部结构无法描述；α=0.1时，可以表现出树冠的凹凸表面；α=0.05时，可以表现出其分枝特性；α=0.02时，可以构建出精细的三维模型，能够较详细地表示树冠内部形状、疏密程度的变化；但减小到一定值时，得到的图形是一些离散的面片，重建结果不完整，不能形成树木模型。

利用alpha-shape算法对树冠进行三维重建时，在参数变化过程中，构建的三维模型也在有规律地变化；树冠体积与冠幅、冠高、胸径等相关性也在有规律地变化。可以看出，不同参数α构建的三维模型能够反映树冠的空间伸展形态、曲面体积、分枝特性及树冠规则性等结构参数，研究结果可作为冠层结构参数计算的研究基础，相关内容将会进一步研究。