PIV系统测量误差的评价方法研究

， ， ， ，

(中国空气动力研究与发展中心，四川 绵阳 621000)

0 引言

PIV速度场测量的精准度，是衡量试验结果优劣的最根本依据，是型号单位和试验单位必须面对和关心的问题。PIV结果的精准度受制于很多因素，包括硬件设备、粒子投放、互相关算法、光学环境等，必须综合考虑。一般来讲，PIV生产厂家在售出仪器前就已经对其进行了系统标定, 并提出了一个速度精准度的经验指标，但由于各自算法的差异，还没有一个普遍的通用准则出现。实际应用情况的测试误差要比理想环境大的多，因此具体应用之前，首先应当对其测试精准度进行分析。

针对具体的测试对象，除了进行严格的标定和合理使用恰当的粒子外，使用基准速度场获得的精准度可以集中反映相机聚焦、激光片光质量、图像预处理、参数设置、噪声消除技术等对测试结果的影响程度。基准速度场大体分为两类：一是利用计算机模拟生成基准流场研究测量结果误差；另外一种是采用一些不可压缩定常流作为基准速度场，对实际PIV系统测量误差进行估计和分析。无论何种方法，基准速度场都是PIV系统误差实验评价的关键问题。

国外由GartEur、EUROPIV、PivNet组成的联合机构从2001年开始组织了PIV算法的挑战赛, 通过各家研究机构对相同的真实及合成PIV图像的分析来实现对算法的比较, 对比结果精度和计算效率，以期实现对算法的优化和改进。到目前为止还没有出现一种算法能让研究者公认为最优。2008年以来，ITTC(国际拖曳水池大会)和HTA(水动力学试验联盟)前后启动了水动力学领域的基准流场研究工作，分别初步提出了二维和三维基准流场的设计方案，但结果相差较大，目前还未有统一标准。

2005年，董明哲[1]等人利用匀速转动圆盘上粒子的反射光模拟流场中示踪粒子散射光实现基准速度场，建立了一套二维PIV系统的精准度评价系统，但装置比较简单，其测量速度只有8m/s。2009年马政[2]等提出了基于DSP处理技术的高精度速度标准源设计方案，但其稳定性有待提高。2013年程素斌[3]等人探索了水中PIV试验测试流场与CFD模拟结果的校核方法，给出了基准模型周围流场结果。

随着定量流动显示与测量技术的地位越来越重要，有必要建立一套标准速度场装置，对测量误差的评价方法进行深入研究。

本项目的目标是研制PIV基准速度场系统、建立PIV系统测量误差的评价方法，实现PIV系统实际测量误差的标定，为试验数据结果提供依据。

1 PIV基准速度场系统研制

如图1所示，高精度PIV基准速度场装置[4]主要由基座、电机、同步带(轮)、镗头、刀柄、转盘、保护罩等组成。高速电机通过同步带轮将动力传递到镗头上，带动安装在刀柄上的转盘旋转。转盘圆周面上布满近似随机分布的粒子，粒子的线速度即为PIV可测量速度。通过速度计算值与PIV测量值对比分析，即可评价PIV速度测量误差。

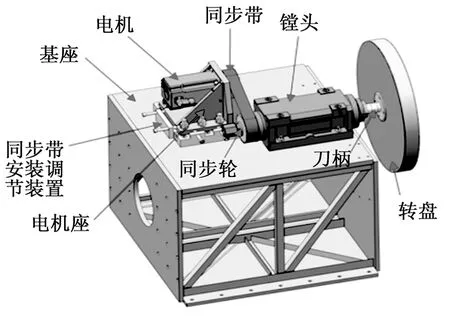
图1 基准速度场装置结构图

主要通过以下技术途径保证高精度的转速控制：

1)优化的系统设计确保传动比为1：1，使得转盘所需转速即是电机转速。系统的胀紧套装配受力后弹性变形与电机轴、左同步轮联结为一体，同时实现轴向、周向定位锁紧。依照节矩越小，传动精度越高，中心距越短，则允许传动速度越高的原则，确定同步轮(带)的节矩与中心距，齿形选择弧齿，同步带材料选用橡胶。转盘直径0.5 m，加工精度控制在±0.05 mm以内。

2)采用先进的基于PC的控制技术和高速以太网总线EtherCAT技术相结合的整体控制系统解决方案。控制系统采用EPC作为硬件平台，结合TwinCAT实时内核，使其成为一个实时运动控制器，可以对电机轴进行高精度实时运动控制。高精度编码器反馈达20 bit，运动控制驱动部分采用先进的高精度AX5000系列伺服驱动器并结合电机，通过EtherCAT工业实时以太网总线与控制器相连。控制系统软件设计基于TWINCAT PLC软件，实现精确运动控制。

主要通过以下技术途径实现高速转盘的稳定性：

1)选用可靠的伺服电机[5]。选用的电机在400 VAC电压下，电机额定转速7300 rad/min，理论最高转速9000 rad/min。电机实际最高转速可达7746 rad/min，对应速度约为203 m/s，满足实验对转速的需求。

2)确保系统基础的稳定。为了保持转盘高速旋转时系统平稳不振动，基座设计为大刚度框架式结构。基座安装在平台(平面度176 μm)上，基座上下安装平面平行(平行度优于120 μm)，以保证转盘旋转轴始终平行于水平面。

3)对转盘本身的稳定处理。作为高速旋转部件，转盘材料选为YL12，转动惯量小。在加强筋之间填充了硬质泡沫，最大程度减小了高速旋转时的风阻和噪音。并且在实验前对转盘做动平衡实验。

2 PIV系统标定测量实验

2.1 实验方案

实验方案采用经典的二维PIV测量方法及被标定系统自身的基本互相关处理算法。将速度标准系统安装在检定合格的平台上并调平固定；选取适合视场大小的镜头及测量距离，使相机正对测量区域，镜头平面与测量平面平行；调整激光，使其均匀照亮测量区域，利用系统自带的采集软件通过同步控制器控制相机与激光器同步触发采集。具体流程如图2所示。

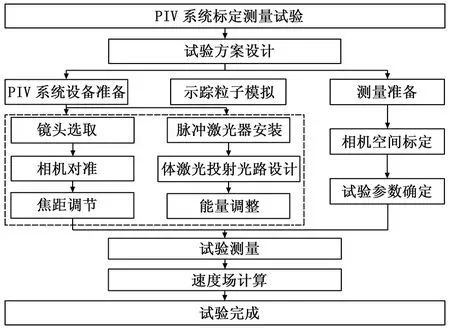
图2 PIV系统标定测量实验流程图

实验用某公司生产的高频PIV系统，分辨率1024×1024 pixel，最大频率3.6 kHz，最小帧间隔 <1 μs，动态范围12 bit，激光器波长527 nm，激光器能量2×100 mJ@50 Hz。

2.2 示踪粒子模拟方法

区别于传统的PIV试验粒子投放方法，由于无法通过投放固态或汽态的粒子材料在高速旋转的圆盘表面来完成，因此本项目采用在圆盘边缘贴黑底白点的贴纸的方法来模拟示踪粒子，贴纸上打有随机分布的点。使用Matlab中的randon()命令生成随机分布点，设计效果如图3所示。

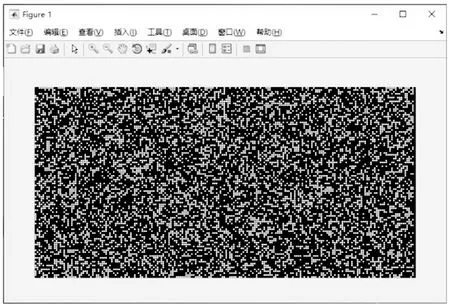
图3 示踪粒子模拟Matlab设计结果示意图

2.3 体激光投射的PIV测量方法

传统的PIV测量采用的是片光照明，但在本实验中测量面并不是在空间中，而是在圆盘的表面，片光并不适用。因此采用体激光投射到测量表面的照明方法，基本原理如图4，利用柱面透镜成像是使光束在单方向放大的特点，利用两组正交的柱面镜，即可实现体光束的成型，根据光斑大小和所需照明的面积计算焦距等参数。

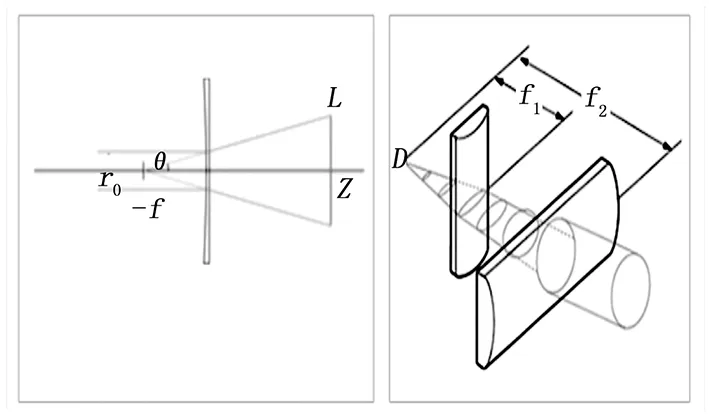
图4 体激光成型原理图

2.4 实验流程

采用典型的二维标定方法，由已知的圆周宽度对应的像素大小换算得到图像放大比。利用系统采集软件控制同步器同步触发相机与激光连续采集50对图像并保存，通过公式计算dt值，代入视场大小与相机分辨率进行计算。

由于不同系统的算法存在一些差别，为了完成相应系统的误差整体标定，利用系统自身的软件进行基本计算。选定计算区域，取互相关计算窗格16×16像素，迭代1次，无其它修正。分别计算出每对图像的速度场。

图5 速度场计算结果图

为进一步减小误差，首先对计算的所有结果取平均。由于被测量旋转圆盘的圆周面是一个弧面，整个区域速度分布并不相等，相机虽已正对测量区域，但其水平度及各方向的倾角误差仍不可能完全消除。因此，取纵向任一直线上分布的速度最大值为最终测量结果，可以有效避免以上问题。最终以每次测量的最大值作为结果数据。

3 误差分析方法研究

3.1 PIV系统误差来源分析

一般地认为， PIV系统的测量误差和若干方面有关系，比如：1)粒子图像中颗粒的粒径大小；2)粒子图像中颗粒的实际位移尺寸；3)粒子图像中颗粒的浓度；4)粒子图像灰度等级；5)粒子图像背景噪音；6)流场中速度变化梯度；7)粒子垂直于片光运动造成的粒子丢失；8)双脉冲激光器外触发的稳定性和一致性；9)同步控制器的触发信号精确度；10)PIV系统软件的参数选择和处理方式；11)PIV系统的实验方案设计；12)操作人员的经验。

总的来说，PIV系统的测量误差主要来源于系统误差和随机误差。但是在实际PIV系统中，由于存在复杂的光学系统、激光器系统、同步控制器、软件计算等等各个环节，很难明确的区分系统误差和随机误差。因此在实际评价PIV系统总的测量误差时，通用的办法是采用测量偏差或不确定度的方式，同时PIV系统作为一个测量仪器，也可以使用一个标称误差来标示。

因此，为了考核PIV系统的整体误差情况，其误差主要就来源于速度基准系统提供的速度场误差。

3.2 速度基准系统不确定度分析

根据现代误差理论，用测量不确定度表示速度基准系统的误差程度更具有合理性与实用性[6-12]。

系统提供的标准速度场速度值由以下公式计算：

v=ωr=2πnr/60=πnd/60

式中，v为线速度(m/s)，ω为角速度，n为转速(rpm)，r为半径(m)，d为直径(m)。

因此，速度的误差直接来源就是转速与直径。

3.2.1 测量方法

用误差为0.03%的转速表测量转速，每组转速测量6次。用分度值为0.01 mm的游标卡尺测量圆盘的直径。

3.2.2 不确定度评定

由于测量结果是不同转速下的多个序列值，以下以200 rpm为例进行不确定度评定，其它同理，结果见表1。

1)直径d的测量重复性引起的标准不确定度分量u1

由直径d的10次测量值求得平均值的标准差σ′=0.0002838 m，标准差由以下公式计算：

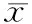
则直径d的测量标准不确定度=σ′=0.0002838m。

根据误差理论，函数系统误差传递公式为：

∂f/∂x1(i=1,2,…n)为各个直接测量值的误差传递函数，Δx1(i=1,2,…n)为各个直接测量值的误差。

故由直径测量重复性引起的不确定度分量为：

其自由度v1=10-1=9。

2)转速n的测量重复性引起的标准不确定度分量u2

由转速n的6次测量值求得平均值的标准差σi如表4，则转速测量的标准不确定度un=σi。

故由转速测量重复性引起的不确定度分量为：

其自由度v2=6-1=5。

3)游标卡尺示值误差引起的标准不确定度分量u3

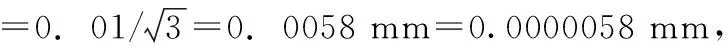
取相对标准差10%，则自由度：

4)转速表示值误差引起的标准不确定度分量u4

取相对标准差10%，则自由度：

3.2.3 不确定度合成

因上述各不确定度分量相互独立，故合成不确定度为：

其自由度为：

3.2.4 展伸不确定度

取置信概率P=0.95，自由度v=15.7，查t分布表得t0.95(15.7)=2.12，即包含因子k=2.12，则展伸不确定度为：

U=kuc=0.008

3.2.5 不确定度报告

速度基准装置在该转速下的速度不确定度U=0.008，是由合成不确定度uc=0.0037及包含因子k=2.12确定的，对应置信概率P=0.95，自由度v=15.7。

依据表1拟制出速度与不确定度对比曲线以及速度与相对误差对比曲线，如图6、图7所示。

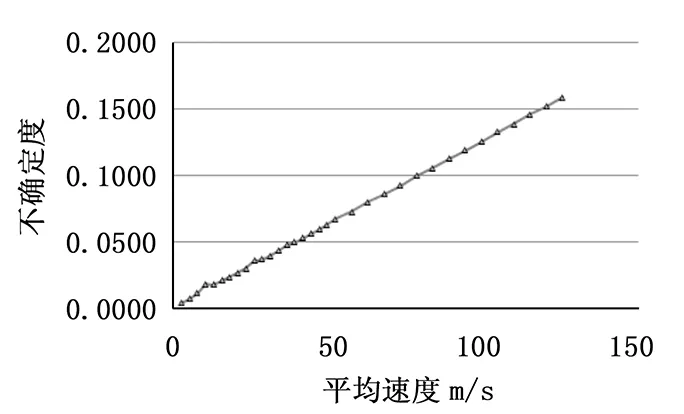
图6 不确定度分布曲线

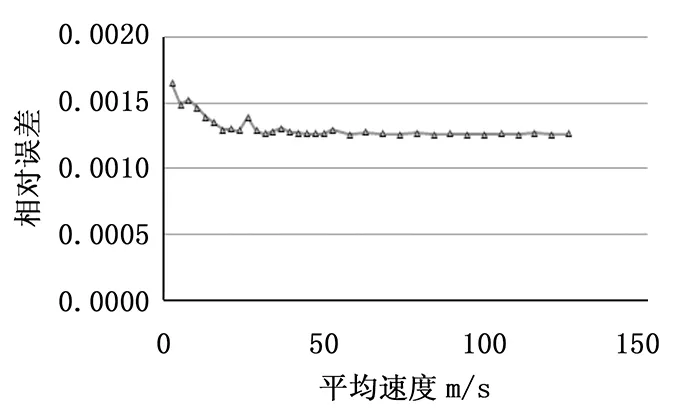
图7 相对误差分布曲线

由以上图表可以看出，速度不确定度随着速度增大而增大，但相对误差保持在一定水平，最大相对误差0.17%。满足对PIV系统进行标定的误差要求。

进一步地给出转速与速度对应关系曲线，如图8，并拟合出线性公式。

表2列出了基准速度参考值以及对应的测量结果，并计算出了相对误差，图9给出了测量结果误差分布图。

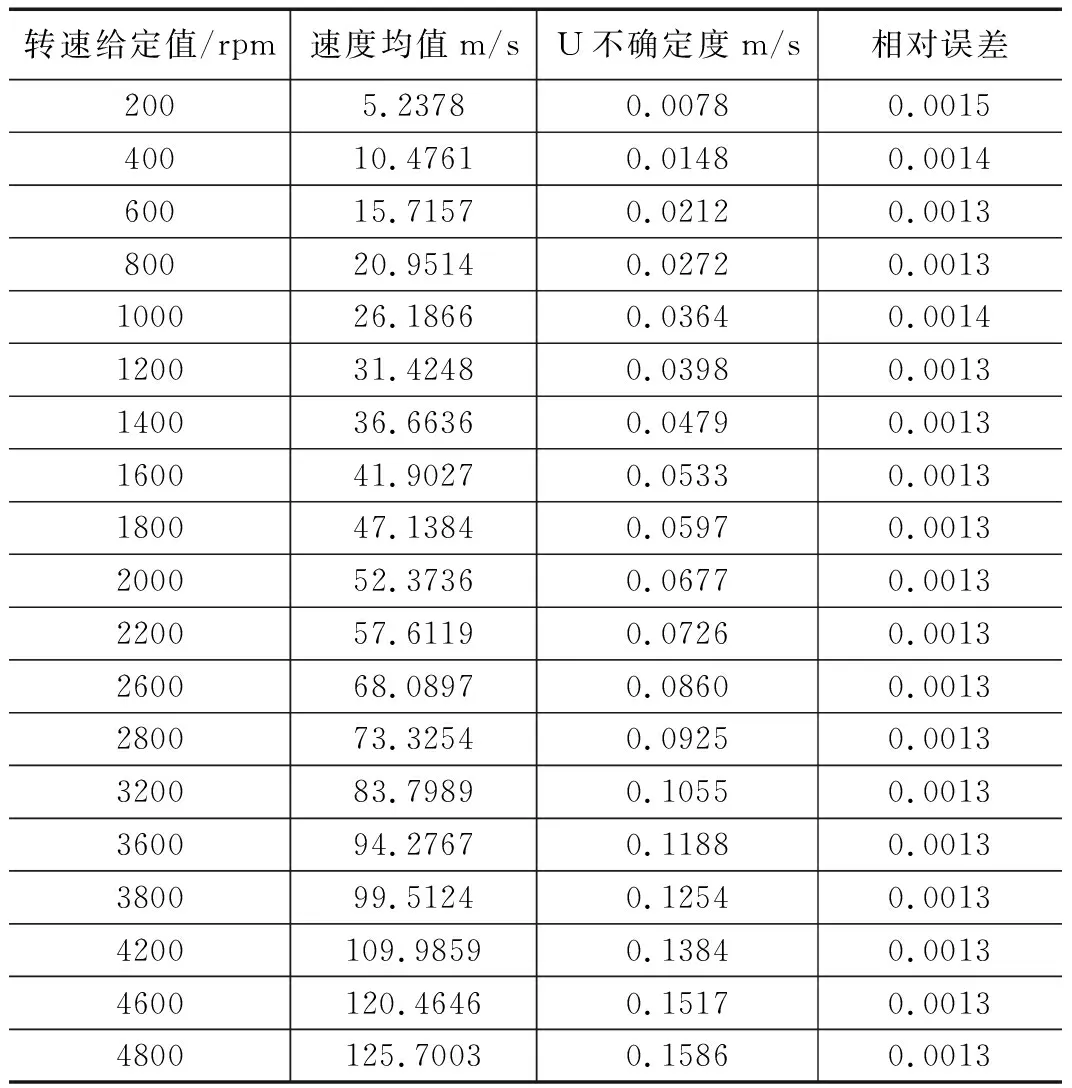
表1 速度标准装置误差分析结果

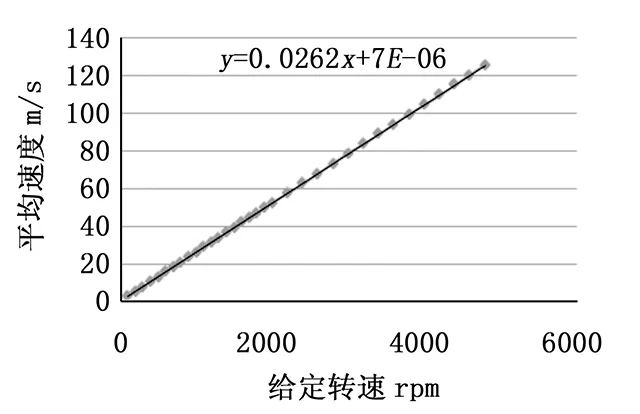
图8 速度标准装置转速与速度对应关系曲线

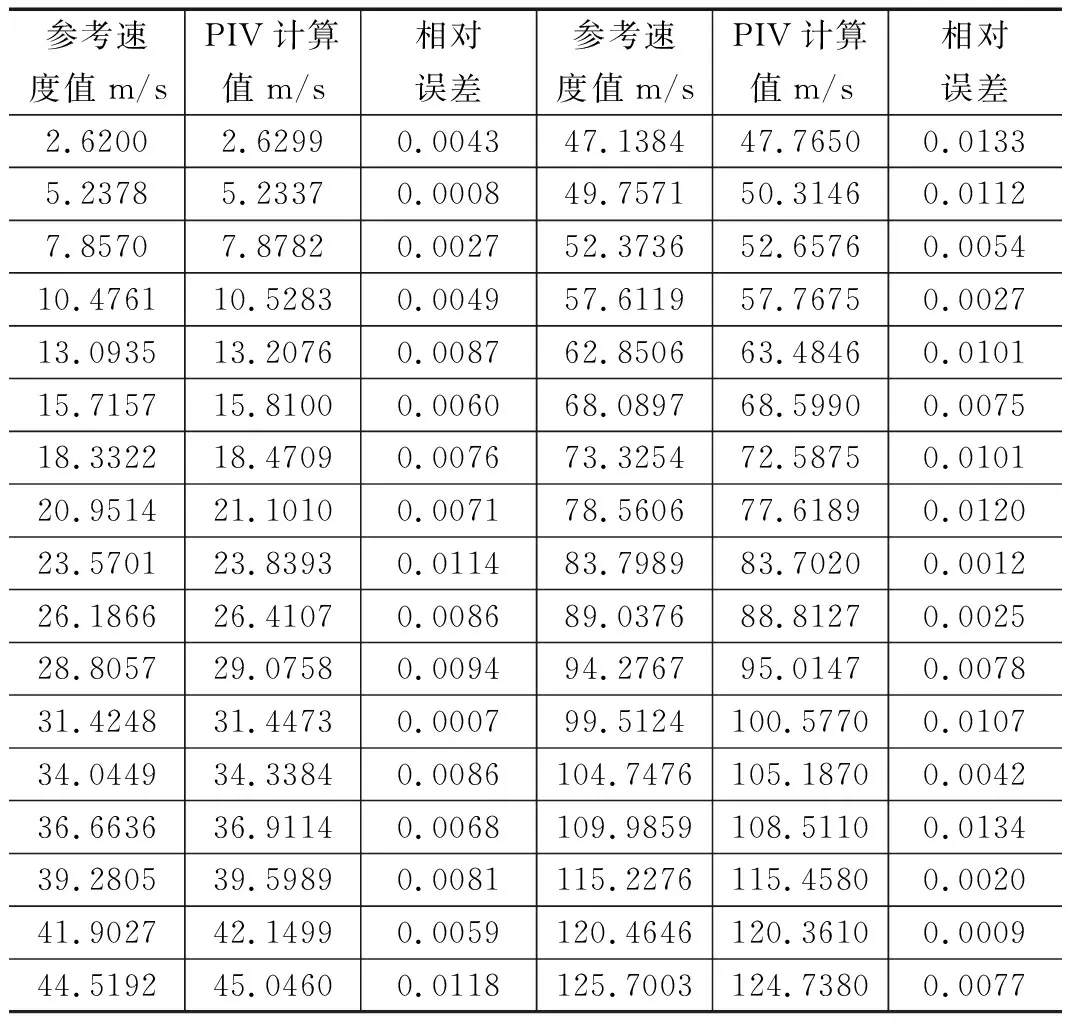
表2 PIV测量数据分析结果

取最大相对误差0.0134，即本PIV系统的测量精度为1.34%。

综上，我们首先分析了PIV测量误差的来源，得到其主要来源是基准速度场的误差；然后运用典型误差分析理论对本项目研制的速度基准系统的速度不确定度进行了考核与分析，得到其最大相对误差为0.17% ，满足对PIV系统标定的精度要求；最后对PIV测量结果与基准系统的参考速度进行比较，得到本套PIV系统的最大测量相对误差为1.34%。

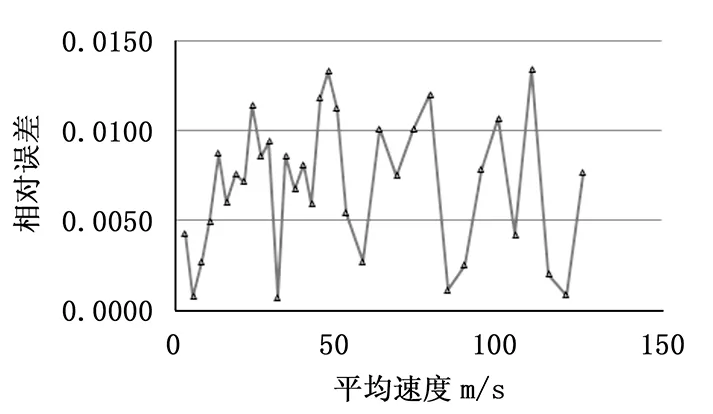
图9 PIV测量结果相对误差分布曲线

4 结论

本文通过设备研制、分析实验测量与理论，系统的建立了PIV系统测量误差的评价方法，实现了对PIV系统实际测量误差的标定，提出了一种考核PIV系统误差的新方法。其主要意义在于：

1)该方法可有效对PIV设备引入的误差进行试验评估，可以作为PIV试验之前进行测量系统地面调试的手段，为PIV试验数据的可靠性分析提供依据。

2)该方法可为PIV算法研究提供一个标准的试验平台，测试不同的算法的准度、精度、可靠性等参数，进行比较。