舰船目标光学特性模型构建

，，

(中国人民解放军战略支援部队航天工程大学，北京 101400)

0 引言

已经有许多学者开展了舰船目标的研究。但大多数学者对于舰船目标的研究主要体现在目标检测与识别上，王彦情、马雷等[1]分析了光学遥感图像关于舰船目标的识别，通过海陆分离，分别考虑离岸舰船候选域和靠岸舰船候选域来进行舰船目标的确认，并总结分析了现有的一些舰船目标检测与识别的方法。赵英海等[2]提出了一种新的可见光遥感图像舰船目标检测方法。该方法是基于标准差特征平面Contrast box 滤波。并且很好处理了舰船图像中黑、白极性问题。冷祥光等[3]对影响星载SAR舰船检测的3个方面进行了分析，并对舰船检测的发展情况给出了预测。

舰船目标的红外辐射特性也是一个重要的研究方向，美国的Environmental Research Institute of Michigan 将目标和海面背景结合，采用一种较为精准的方法对目标与海面背景进行红外模拟，称为舰船与海面图像模拟包[4]。沈国土和杨宝成等[5]采用面元拉伸的方法建立了具有厚壳结构的舰船几何模型。在海面模型的基础上，发布了整套针对舰船红外辐射场模拟的软件[6]。任海霞等[7]利用RIS 模拟了不同天气状况、不同观测视角的舰船红外热像。

由前面分析知，舰船目标的检测与识别已经发展的很好，并且各种方法也日益增多。并且舰船的红外辐射特性研究也已经很成熟。但是对于舰船目标的光学特性都没有进行一个系统的分析。舰船的光学特性是对舰船进行探测与识别的基础。舰船目标的光学特性模型关键在于计算不同出射方向上的辐亮度。本文首先研究了舰船目标表面的面元分析方法，分别分析了BRDF模型、坐标转换、大气环境影响效应。最后建立了舰船目标光学特性模型并利用Matlab进行了仿真分析，得到了不同波长下的舰船入瞳辐亮度。

1 舰船目标光学特性模型

1.1 BRDF简介

双向分布函数是材料的基本物理参数，用来描述材料反映特性在2π空间内的分布。BRDF的定义[8]如下式：

Fr(θi,θr,φ)=dLr(θr,φr)/Li(θi,φi)dΩi=

dLr(θr,φr)/dEi(θi,φi)

(1)

其中:Fr为目标双向反射分布函数，单位为sr-1；dLr为出射方向的辐射亮度；Li为入射方向的辐射亮度；dΩi为入射方位的立体角；dEi为入射到目标表面的辐照度；θi为入射角；θi为探测角；φi为入射方向的方位角；φr为探测方向的方位角；φ=φr-φi为散射光出射方向与光源入射方向的方位角度差。

根据目标的表面状况以及实际光照环境，双向分布函数选择Cook-Torrance[9]模型。BRDF的表达式为：

fr(θi,φi,θr,φr)=sRs+dRd

(2)

其中:s+d=1,Rs是镜面反射分量，Rd是漫反射分量。s和d表示两个分量所占的比例。

Rd=ρ/π

(3)

(4)

(5)

(6)

其中:ρ为目标材料的方向半球反射率，F为菲涅耳反射系数，δ为法向量与入射出射角平分线的夹角；β为入射方向与入射出射角平分线的夹角。

对BRDF的理论分析和计算，通常用到的理论方法为菲涅尔公式和微面元分析法。

微面元分析法的思想最早见于K.E.Torrance和E.M.Sparrow[10]在1966年发表的文章中，微面元分析法的核心思想是将目标宏观表面划分成一个个微观的小面元，将每个微观的小面元都当做一个计算单位，这样可以便于后面分析每个微小面元散射情况，可以避免对大的曲面进行计算时，很难进行光散射的计算。这也是将复杂的问题简单化，便于后面进行求解，体现了微面元分析法的优越性。微面元的划分方法常分为三角面元法、多边形面元法等。三角面元法在进行分析时更适合比较复杂的曲面，舰船目标本身结构都比较复杂，并且一些结构连接点用三角面元法更便于划分。进行了微面元划分后，近似认为每个微面元为由目标材质构成的理想光滑表面，微面元法线方向的分布，则一般被认为服从高斯分布或Beckmann分布。这样对于每一个微面元可以通过几何光学法和菲涅尔公式分析其光学散射特性。

1.2 舰船目标表面的面元分析方法

选取比较简单的舰船做为研究对象，该舰船长252 m，宽43.4 m，高43.6 m，在进行建模时，只是对舰船的整个表面进行了描述，对于一些铆钉等细小的零部件进行了忽略。如图1所示，首先通过3DS MAX软件进行模型几何建模，再对目标进行三角面元划分，最后对有效面元进行判断，得到可视的有效面元。

1.2.1 几何模型构建与面元划分

本文选取了舰船目标作为研究对象，舰船目标所反射出的辐亮度主要在于船身，为了便于最后的辐亮度的计算，在对舰船目标进行3D建模时，对船身上一些部件进行了简化，对于舰船身上一些比较小的盒体进行了简化，这些盒体相对于整个舰船来说还是比较小的一部分，并且由于面元的一些遮挡，当去掉这些盒体时，暴露出的舰船船身和盒体产生的辐亮度相差不大。具体如图2所示。

图1 舰船模型 图2 简化舰船模型

对于建立的舰船3D模型，3D MAX软件默认采用了三角面元进行划分，这也和前面分析三角面元的优势得到了体现，使得在舰船一些连接点和面与面连接边处，三角面元更易进行面元划分，这也使得整个网格划分显得比较连贯。软件并自动计算了各个面元的法向量信息。通过3D MAX软件以*.ASE文本的形式保存了3D模型的所有的信息，便于后面编程进行读取。最后得到了1694个顶点和3043个面元的信息。舰船网格化为如图3。

1.2.2 有效面元判断

对于有效面元的判断，存在两类情况：一种是面元未被入射光照射到，另一种是面元散射光未被探测器接收。只有当两种情况都不满足的面元才是需要最后计算的，这在最初的计算可以去掉一部分不满足要求的面元，这可以大大减少运算量。为了简化计算，都将以面元中心点是否被遮挡进行判断。对于这两种情况，就是判断入射光线、面元的法向量、探测器探测方向三者之间的关系，具体情况如图4所示。

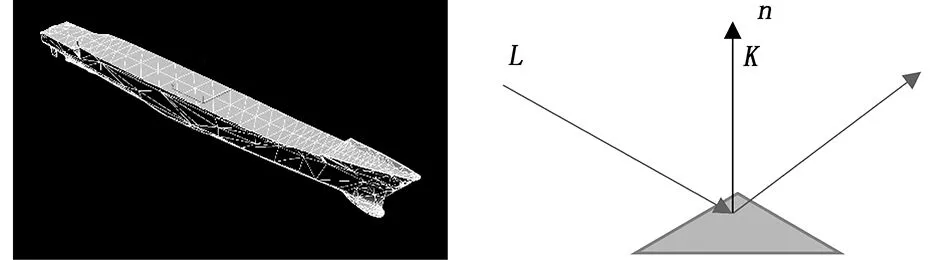
图3 舰船网格 图4 面元有效示意图

其中：入射方向为L，面元法向量为n，出射方向为K。有图4可知，只有当面元的法向量与入射方向的反方向和出射方向的夹角都为锐角，则面元反射的太阳光线能被探测器接收到。即:

L.N<0和K.n>0

1.3 坐标转换

1.3.1 坐标系定义

在计算舰船目标散射特性时，需要将太阳-目标-探测器统一到一个坐标系下，需要用到以下几个坐标系：

1)大地坐标系：地球椭球的中心与地球质心重合，椭球的短轴与地球自转轴重合，采用大地经度L、纬度B和大地高H来描述空间位置。

2)地心固定坐标系：地球质心为原点，X轴在赤道面内指向格林尼治恒星零时，Z轴垂直于赤道面，与地球自转角速度矢量一致，Y轴在赤道面上垂直于X轴。三轴符合右手坐标系。

3)目标基准坐标系：舰船目标质心为原点，Xw由原点指向船头方向，Zw垂直船平，Yw轴垂直Xw轴，三轴符合右手坐标系。

4)面元坐标系：面元中心为原点，面元法向量为Z0轴，将过目标面元中心点的面元切平面A与平行于目标本体坐标系的平面B的交线定为X0轴，Y0轴在面元平面上垂直于X0轴。三轴符合右手坐标系。

1.3.2 坐标系转换关系

1)大地坐标系与地心固定坐标系的坐标转换

大地坐标系与地心固定坐标系变换公式为:

(7)

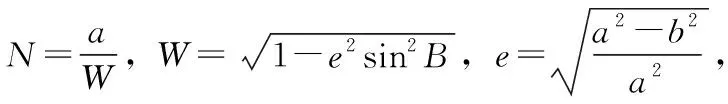
2)地心固定坐标系与目标基准坐标转换

地心固定坐标系与目标基准坐标系之间的变换为刚体变换，即只进行平移、旋转等变换，而不会改变坐标系内两点间的距离。

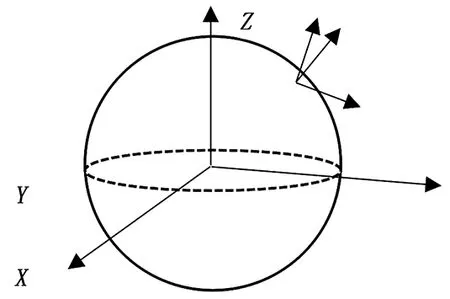
图5 坐标示意图

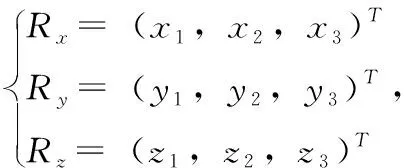
(8)

因而两者坐标系可以用旋转矩阵R和平移向量t来描述。

3)目标基准坐标系与面元坐标系

目标面元中心点在目标本体坐标系中的坐标为(xk0,yk0,zk0)，面元坐标Z0轴为目标面元中心点的法向量nk，方向数为(nk-x,nk-y,nk-z)，则其单位方向余弦矩阵为：

(9)

式中,

(10)

下标k代表第k个面元。

目标面元中心点的面元切平面A与平行于目标本体坐标系的平面B的交线定为X0轴，面元切平面A的法线方向即为nk方向；平面B的法线方向即为目标本体坐标系Ow-XwYwZw的轴方向，其方向数为(0,0,1)。对其进行矢量积运算X0=nk×Zw，整理得到X0轴的单位方向余弦矩阵为：

Xk=[Xk-x,Xk-y,Xk-z]=

(11)

Y0轴为过目标面元中心点(xk0，yk0，zk0)且同时与X0轴和Z0轴垂直的直线，通过右手法则进行矢量积计算，类似X0轴计算，通过计算整理,最终得到Y0轴的单位方向余弦为：

Yk=[Yk-x,Yk-y,Yk-z]=

(12)

由式(9)～式(12)可得，从目标本体坐标系Ow-XwYwZw到目标面元坐标系Oo-XoYoZo的转换矩阵Uk为：

(13)

1.4 大气环境影响

由于大气中存在多种气体以及微粒，如尘埃、烟、雾、雨、雪等，使光的传输特性发生变化。在目标表面散射光经过大气到达探测器的过程中，光线与大气中的分子、气溶胶等发生相互作用，产生大气吸收、折射、散射、湍流等现象。其中，大气环境对舰船目标光学特性模型的主要影响主要是由于在经过大气的过程中目标表面散射光的能力产生了衰减，而这一衰减之后的能量与透过之前能量的比值被称为这部分大气的大气透过率。影响大气透过率的最主要因素是大气分子和气溶胶的影响[11]。

大气分子主要包括N2、O2、CO2、H2、H2O等，其中占90%的N2、O2对可见光和近红外几乎不吸收，对远红外和微波会表现出很强吸收，CO2、H2O是对可见光和近红外吸收的重要吸收分子。大气中除大气分子外，还存在尺寸较大的大量固态、液态微粒，包括尘埃、烟粒、微水滴、烟粒及有机微生物等。这些微生物在大气中的悬浮成溶胶状态，称为气溶胶，气溶胶也存在对光的吸收和散射作用[12]。

综上所述，大气中对可见光散射吸收的主要成分为CO2分子、H2O分子和气溶胶粒子，对于这3种成分对于大气透过率的贡献都不一样，需要对3种成分进行不同的分析，然后将它们进行相乘得到最后大气透过率。接下来将对不同的吸收分子进行阐述。

1)CO2分子透过率的计算

采用pierlusi计算公式[13]，透过率为:

τ1=exp(-10ax)

(14)

式中,

x=C1+log10W

(15)

(16)

其中:μ为吸收体含量，可以表示为：

(17)

其中:P为大气压力；Po为标准大气压力；T为大气温度；ρa为气体密度；z为路径长度；M为吸收体混合密度比；C1、a、n、m为与波长有关的参数。

2)H2O分子透过率的计算

H2O分子透过率计算公式为[14]：

τ2=exp(-10αo+α1B)

(18)

式中,

(19)

其中:取a0=-1.14619，a1=0.55257，n=0.86964，m=0.27658。

1)气溶胶粒子透过率的计算

气溶胶的粒子透过率为：

(20)

其中:q为与能见度有关的参数，当能见度很高时，q=1.6；当能见度一般时，q=1.3；当能见度小于6 km时，q=0.585V1/3。

综上所述，大气的通过率为：

τ=τ1×τ2×s(λ)

(21)

1.5 舰船目标光学特性建模

卫星在对舰船目标进行侦察时，主要是接收到目标反射过来的太阳发照光，由普朗克黑体辐射公式，黑体辐射的照度为公式。

(22)

式中，λ为波长(μm)，T为黑体的温度(K)，通常太阳被认为温度为5000 K的黑色辐射体，C1=3.742×10-4W·μm2为第一辐射常数，C2=14388 μm·K为第二辐射常数。面元产生的辐照度如图6所示。

图6 太阳-目标面元-探测器三者关系示意图

每个单位面元相对于太阳和探测器的位置都不同，所以在进行计算时需要计算每个目标面元所产生的辐亮度，最后再进行叠加才能得到结果。则一个单位面元上所接收到太阳辐亮度为：

(23)

式中,S为太阳的表面积，Rsun为太阳到面元的距离。

在面元出射方向上的辐亮度为：

(24)

探测器接收到的辐亮度为：

(25)

式中，Robv为探测器到面元的距离,τ为大气通过率。

则所有面元产生的辐亮度为：

(26)

在谱段λ1到λ2产生的入瞳辐亮度为:

(27)

舰船目标光学特性建模过程如图7所示。

图7 光学散射特性计算流程

1)将探测器和目标的坐标由大地坐标系转换到地心固定坐标系，将经度、纬度、高程坐标转换为X、Y、Z坐标表示。

2)根据太阳和探测器与目标的相对位置，计算出在目标基准坐标系下太阳和探测器的坐标。

3)根据每个面元的在目标基准坐标系下的法向量，将太阳和探测器的坐标转换到面元坐标系下，计算每个面元的入射角、出射角和方位夹角。

4)判断面元是否为可成像面元，为下面的计算首先剔除一些不符合要求的面元。利用前面分析的面元消隐很容易就得到。

5)计算目标面元接收到的太阳辐射能量。

6)依据面元材质，选择适合的BRDF模型，计算面元的光辐亮度。

7)结合大气透过率，遍历全部面元，计算入瞳处的光辐亮度。

2 仿真分析

将3DMAX生产的数据导入Matlab当中，并且在Matlab将所有点依次连接成舰船模型，所得到的图像为图8。

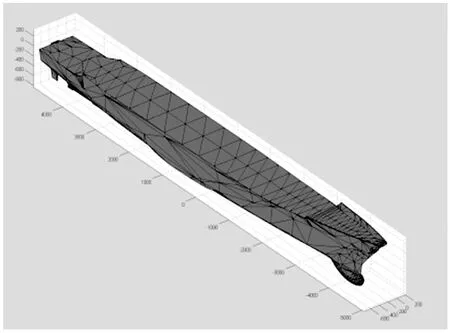
图8 Matlab生成的舰船模型

由图8可知，Matlab中生成的舰船模型与3D MAX所建的模型在形状和大小上保持一致，这也表示从3D MAX导出的舰船模型数据是可信的，这为接下来的计算打好了基础。

仿真只计算可见光波段的入瞳辐亮度，在辐亮度入瞳之前，需要经过大气的衰减，在计算每个波长的入瞳辐亮度都需要将大气考虑进去，所以依据前面分析得到的大气透过率公式进行仿真。得到了大气透过率随着波长变化的示意图。

图9 大气透过率与波长关系示意图

为了便于进行仿真计算，将目标和探测器的位置进行了设置，具体数字如下。

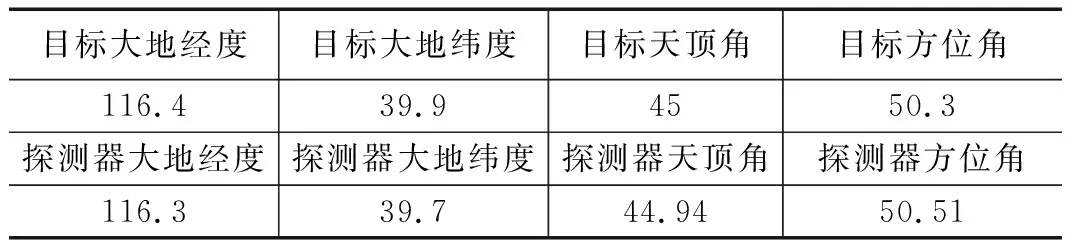
表1 目标、探测器参数

最后利用Matlab计算得到了不同波长产生的入瞳辐亮度，具体如图10所示。

图10 辐亮度与波长关系示意图

结合大气透过率与波长的关系图，可以发现大气透过率决定着辐亮度的变化趋势，所以大气对于入瞳处辐亮度的计算起着非常重要的作用，因此若是对某区域进行侦察，应着重考虑大气对侦察带来的影响。并且最后得到了辐亮度随着波长的变化关系，若要计算可见光的入瞳辐亮度时，只需要积分就可以得到最终的入瞳辐亮度。

3 结束语

该文针对舰船目标，构建了光学特性模型。并且依据仿真软件对所建模型进行了验证，最后得到了大气透过率、辐亮度随着波长变化的示意图。这为分析卫星对舰船的侦察奠定了基础，因为在分析对舰船侦察情况时，需要计算整个系统的信噪比等其他性能参数，这都需要给出舰船在入瞳处造成的辐亮度。

但是本文在计算入瞳处辐亮度进行了许多简化计算有可能造成最后的结果有一定的误差，并且在计算过程中没有考虑背景给计算辐亮度带来的影响。这也可能对最后的计算结果造成一定的影响。

分析了舰船目标在可见光波段的入瞳照度的计算。具有如下特点：

1)基于视觉判断的消隐计算，去除了大多的遮挡面元，为模型的计算进行了简化，运算速度加快。

2)将太阳-目标-探测器统一到面元坐标系下，而模型计算坐标系的建立是面元进行光学特性分析的基础。另外也为面元消隐减少了运算量。

3)在综合考虑大气环境、目标材料等各种影响因素的基础上，提出了一种有效的舰船目标光学特性建模方法。为舰船目标光学特性研究和可探测性研究提供了理论基础。