不确定条件下集装箱船混合目的港贝内排箱问题优化决策

张 煜, 程 昭, 李 俊, 田 维

(武汉理工大学 物流工程学院， 武汉 430063)

集装箱船舶配载优化决策可分为主贝计划问题和贝内计划问题，后者又可细分为单一目的港贝内排箱问题和混合目的港贝内排箱问题。其中，混合目的港贝内排箱问题是将不同目的港集装箱放在船舶贝内具体箱位，需要满足船舶贝内横倾力矩和单列积载强度等要求，减少或避免后挂靠港集装箱压在先挂靠港集装箱之上，确保船舶安全运输与港口有效装卸。目前，已有研究成果多关注确定条件下的船舶贝内排箱问题。DUBROVSKY等[1]使用遗传算法解决船舶混合目的港贝内排箱问题。DELGADO等[2]设计遗传算法求解带有装卸规则集的船舶贝内排箱问题。AZEVEDO等[3]设计遗传算法求解船舶贝内排箱问题。 GEOERIGK等[4]设计鲁棒优化方法求解船舶贝内排箱问题。PARREO等[5]提出基于贪心策略的随机自适应搜索算法来求解船舶配载中的贝内排箱问题。张维英等[6-7]研究单一目的港和全航线的贝内排箱问题，分别用禁忌搜索和隐式图启发式搜索技术求解。孙晓雅等[8]采用粒子群算法求解混合目的港贝内排箱问题。田维等[9]设计了3阶段启发式算法求解船舶混合目的港贝内排箱问题。李俊等[10]考虑堆场发箱顺序对船舶配载决策的影响，设计两阶段算法求解船舶配载的贝内排箱问题。实际中，海关会对外贸出口箱进行查柜，主要以电脑抽查随机布控为主，存在集装箱抽检速度慢或查验不过而导致无法装船的甩/减箱事件，也存在因随机抽检而错过原班次的集装箱需要临时装船的加箱事件，以上统称为不确定条件。因此，对不确定条件下船舶混合目的港贝内排箱问题进行研究，借鉴多阶段动态决策思想，构建任意阶段的数学模型，设计基于插入-分段搜索的启发式算法，通过案例仿真对该算法进行分析和验证。

1 问题描述

不确定条件下的船舶混合目的港贝内排箱问题，是综合考虑海关抽检中所出现的加箱或减箱等不确定事件，对贝内计划进行动态调整，降低不确定事件对船舶贝内计划的影响，提高船舶贝内计划的鲁棒性。在此，按照不确定事件发生的顺序，可将贝内计划动态调整过程转变为多阶段动态决策过程，见图1。根据多阶段动态决策的无后效性理论可知，只要确保任意阶段最优，则整体最优。在图1中：初始阶段将集港箱信息(箱型、箱重、目的港)和船舶贝结构作为已知条件，输入给数学模型，产生初始贝内计划s0；对于任意阶段t，存在不确定事件et和上一个阶段的贝内计划st-1，利用et更新当前集港箱信息，并通过模型Mt生成新的贝内计划st。对于模型Mt，需要最小化st-1和st的差异，即贝内计划调整最小。由于本文关注的是船舶贝内计划中的混合目的港贝内排箱问题，借鉴多阶段动态决策思想，引入阶段概念，在下一节构建该问题任意阶段的0～1整数规划模型。

2 数学模型

2.1 引入集合

2.2 建立模型

任意阶段t∈T的0～1整数规划模型，记为OPM(t)，有

(1)

式(1)为最小化t∈T阶段船舶贝内横倾力矩的目标函数，是t阶段船舶贝左侧集装箱和右侧集装箱所产生的横倾力矩之差，其中：k(t)∈N(t)为在t阶段待装箱编号；p=(i,j)∈P为船舶贝第i列第j层的箱位，i∈I,j∈J；wk(t)为集装箱k(t)的重量；xk(t)p为集装箱k(t)是否装到船舶贝的p∈P箱位，为0～1决策变量；d为集装箱宽度；Δ为相邻集装箱间隙；g为重力加速度。

(2)

式(2)为最小化相邻阶段贝内计划偏差的目标函数。

∀p∈P

(3)

式(3)为t阶段船舶贝内任意箱位最多放入一个集装箱的约束。

∀k(t)∈N(t)

(4)

式(4)为t阶段任意待装集装箱都必须被指派一个船舶贝内箱位的约束。

∀p∈P

(5)

式(5)为t阶段船舶贝内集装箱不能悬空的约束。

(6)

式(6)为t阶段待装箱按发箱顺序装船，先发箱不能置于后发箱之上的约束。

∀i∈I

(7)

式(7)为t阶段船舶贝内任意列的积载强度必须得到保障的约束，其中，STi为船舶贝第i列最大允许的积载强度。

∀p∈P

(8)

式(8)为t阶段依据重量等级船舶贝内集装箱重不压轻的约束，其中，θk(t)为集装箱k(t)的重量等级。

∀p∈P

(9)

式(9)为t阶段船舶贝内不能出现阻塞箱的约束，即后卸船集装箱压在先卸船集装箱之上，其中，dk(t)为集装箱k(t)的目的港，π(p)∈P表示箱位p上面的紧邻箱位。

(10)

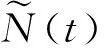
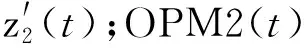
(11)

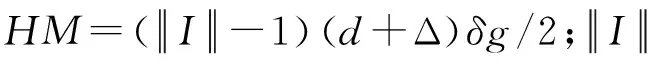
(12)

式(12)为t阶段与t-1阶段的船舶贝内计划偏差约束。

表1 模型扩展

3 算法设计

算法主要思路如下：

1) 在初始阶段运用文献[9]的3阶段启发式算法获得初始解见图2，解的结构见图2a)所示，第1行是待装船集装箱序列，第2行是船舶贝内箱位序列，可实现集装箱与船舶贝内箱位的匹配，例如箱位p3被指派给集装箱c1。

2) 当不确定加箱或减箱事件发生时见图2b)，进入下一阶段t=t+1，更新集装箱序列和船舶贝内箱位序列，减箱事件对应的集装箱c4和箱位p6从序列中被删除，加箱事件对应的集装箱c7被添加到集装箱序列。

3) 执行“插入-分段”操作见图2c)，结合插入位参数值km，将序列划分为两段，插入点之前的集装箱与箱位的匹配关系不变，插入点之后的集装箱需要重新分配船舶贝内箱位。

综上，算法的核心是“插入-分段”与“分段搜索”。前者通过动态调整km，可以获得更小的搜索域，便于OPM1和OPM2模型的分段搜索与求解；后者采取两阶段思想，先通过OPM1最小化相邻阶段船舶贝内计划的偏差，再通过OPM2最小化船舶贝内横倾力矩，解决多目标优化问题。

算法具体流程见图3，其中：No和Po分别为插入-分段操作中插入点之前的集装箱集合与船舶贝内箱位集合，不参与分段搜索；Nr=N(t)No和Pr=PPo表示参与分段搜索的集装箱集合与船舶贝内箱位集合，需要重新为Nr中的集装箱指派Pr中的船舶贝内箱位；其他符号参见上一节的符号定义。

4 仿真试验

通过港口调研，给出仿真试验的基础数据。对于船舶Bay09结构，存在36个待装箱，船舶贝内最大允许横倾力矩为616 kN·m；对于船舶Bay47结构，存在72个待装集装箱，船舶贝内最大允许横倾力矩为752 kN·m；不确定事件涉及2个减箱和2个加箱，合计4个阶段。船舶贝结构见图4，两种场景见表2，例如B09-N36-D3表示船舶贝结构为Bay09、待装箱36个、待装箱目的港数为3。每个场景随机生成5个案例进行仿真试验，分别采用插入-分段搜索算法和CPLEX优化包求解器进行求解，详细仿真结果见表2。CPLEX设定2 h求解时间，在该时间内无法得到输出结果，则在表2中用“/”表示。

表2中，随着船舶贝结构、待装集装箱数目、目的港数等的增大，CPLEX在20个例子中仅能求解9个例子，插入-分段搜索算法能够求解所有例子，表明所设计的算法适合解决不同规模算例。此外，在9个CPLEX和插入-分段搜索算法都可以求解的例子中，CPLEX获得的z2平均值在8个例子中劣于插入-分段搜索算法，表明所设计的插入-分段搜索算法可获得相邻计划调整较小的船舶贝内计划方案，这有利于提高船舶贝内计划的鲁棒性，降低计划编制人员工作负荷。在以上9个例子中，插入-分段搜索算法获得的z1平均值普遍劣于CPLEX，这项指标只要小于最大允许横倾力矩就可以满足实际需要，插入-分段搜索算法在所有例子中的横倾力矩都远小于最大允许横倾力矩。

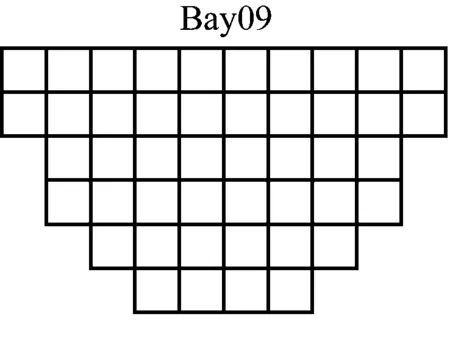
a) BAY09船舶贝结构

5 结束语

不确定条件下集装箱船混合目的港贝内排箱问题，引入海关随机抽检所引发的减箱或加箱等不确定事件，是确定条件下船舶贝内排箱或贝内计划问题的扩展。本文借鉴多阶段动态决策思想，按照事件发生的顺序，将问题划分为多个阶段进行动态决策，构建任意阶段的0～1整数规划模型；结合该模型，设计插入-分段搜索的启发式算法；通过案例仿真，表明所设计的算法满足船舶贝内排箱的各项约束，可提高船舶贝内计划的鲁棒性，降低不确定事件对船舶贝内计划的影响。此外，本文设计的插入-分段搜索启发式算法，部分模块采用CPLEX求解子模型，尽管采用插入-分段操作降低搜索域，但后续研究可以发展求解精度高的启发式算法，予以替换，可进一步提高算法的求解效率。

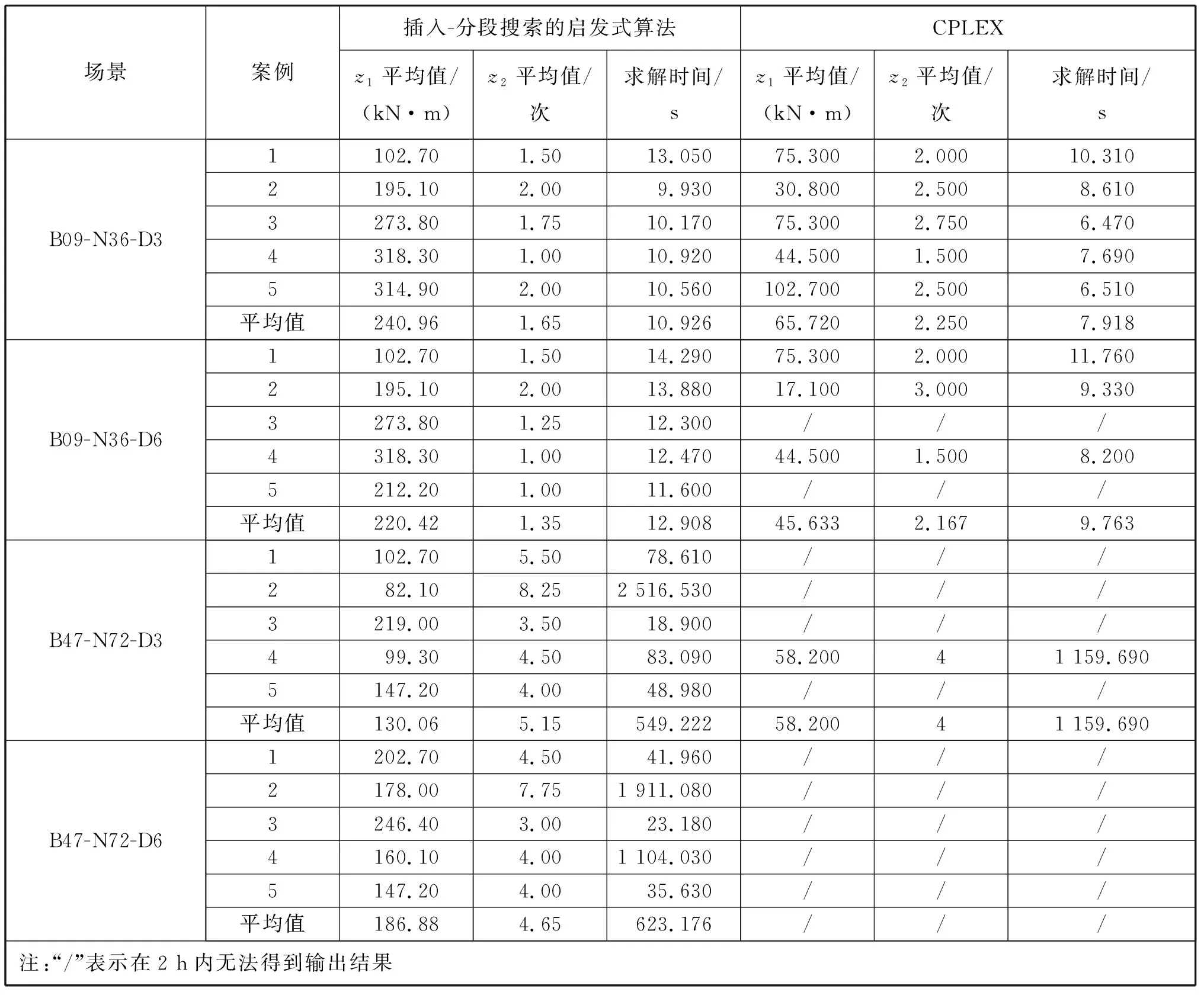
表2 案例仿真试验结果