力偶型径向柱塞马达转矩转速特性分析与实验

闻德生 王 雷 刘春晓

(燕山大学机械工程学院， 秦皇岛 066004)

0 引言

液压马达是将液压能转换为机械能的液压执行元件，现在广泛应用的液压马达主要包括：齿轮式、叶片式、轴向柱塞式、螺杆式和径向柱塞式[1-3]。大多数液压马达工作时，因受到高压油区的侧向力，加速了马达关键零部件的疲劳损坏，降低了马达的寿命[4-7]。而对于径向力平衡的马达，如双作用叶片马达，由于自身结构的限制，无法进行无级变量，导致马达在某些工况下不能满足使用要求[8-9]。

为了解决上述问题，基于双定子思想[10-14]，提出一种基于力偶原理的马达，该马达工作时马达输出轴的径向力平衡，通过合力偶输出转矩。可以输出3种转矩和转速，保证径向力平衡的同时提高马达的调速范围。

1 结构特点和工作原理

力偶型径向柱塞马达结构如图1所示。

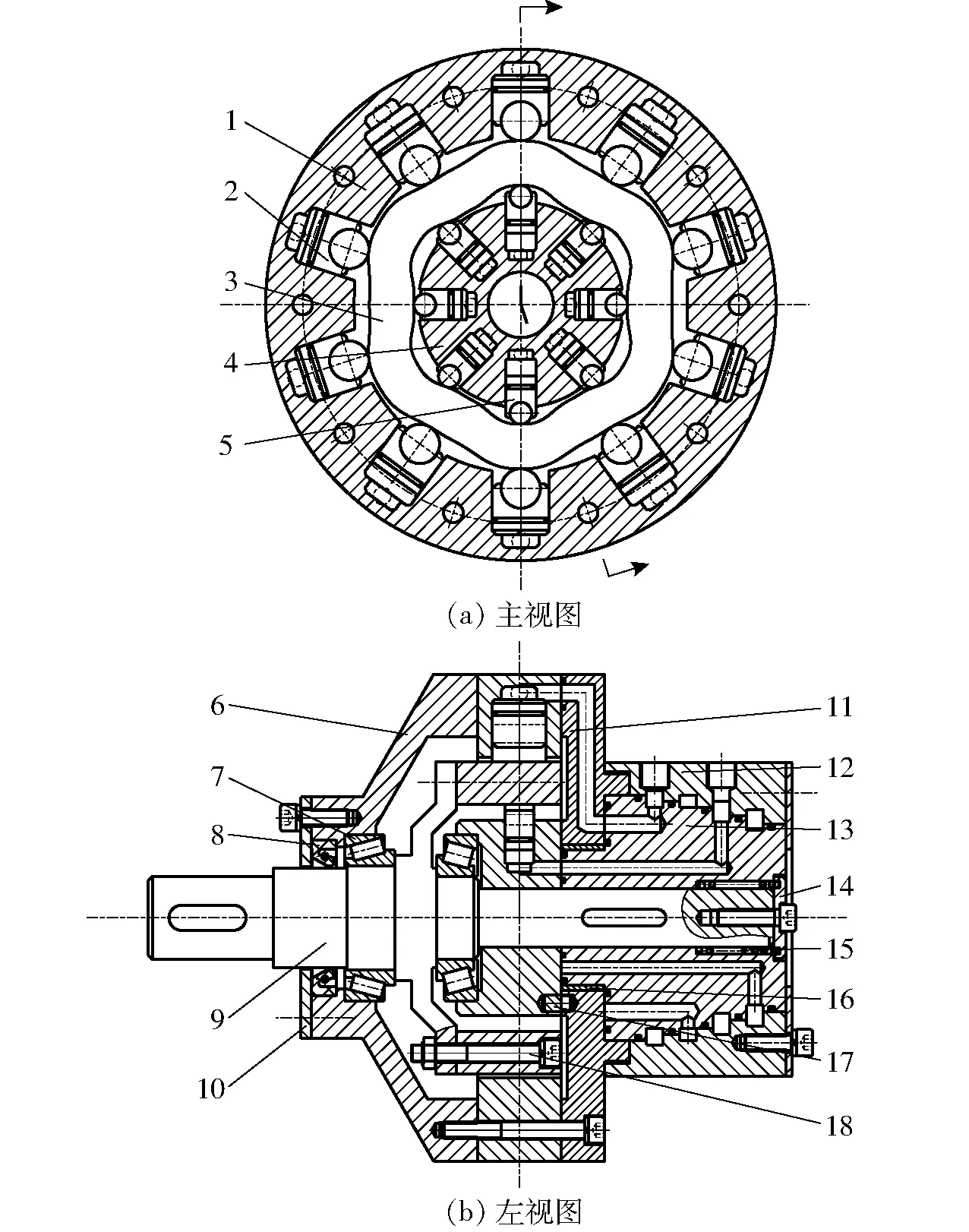
图1 力偶型径向柱塞马达结构图Fig.1 Structure diagram of couple type radial piston motor1.外缸体 2.外柱塞副 3.凸轮环 4.内缸体 5.内柱塞副 6.左壳体 7.圆锥滚子轴承 8.无骨架橡胶油封 9.输出轴 10.左端盖 11.右壳体 12.配流盘壳体 13.配流盘 14.轴端挡圈 15.弹簧 16.滑动轴承 17.圆柱销 18.螺栓

由于马达的内、外缸体相互独立且有独立的配流机构，因此该马达可以在一个壳体内形成内、外2个马达。内缸体、凸轮环的内导轨、配流盘和输出轴形成内马达；外缸体、凸轮环的外导轨、配流盘和输出轴形成外马达。通过不同的配流方式，使马达有3种工作方式，输出3种不同的转矩和转速。

凸轮环与马达输出轴相接，内、外缸体与马达的壳体通过螺栓连接，当在马达的内缸体输入高压油时，油液驱动柱塞径向移动并作用到凸轮环，柱塞对凸轮环产生作用力，该力可分解为切向力和径向力，径向力与作用在柱塞上的液压力相平衡，切向力作用于马达的旋转中心，与关于旋转中心对称的另一个柱塞产生的切向力相等，方向相反且不共线，两个力对凸轮环产生了一个力偶矩，从而驱动马达的输出轴产生转矩。同理，当在马达的外缸体中通入高压油时，外柱塞对凸轮环作用力可以分解为沿缸体半径的径向力和切向力，通过切向力的作用输出转矩。

2 马达瞬时转矩分析

马达转矩脉动是评价液压马达性能的重要参数[15-20]，故对马达3种工作方式下的瞬时转矩进行分析。

2.1 内马达单独工作

2.1.1瞬时转矩

高压油对柱塞的作用产生转矩，各个柱塞产生的瞬时转矩相互作用，合成了马达的瞬时转矩，因此应先分析单个柱塞产生的瞬时转矩。

如图2所示，柱塞与凸轮环的作用力分解为径向力和切向力，切向力对输出轴产生转矩，可得单个柱塞的理论瞬时转矩为

Ti=Ftiρi=Fpitanβiρi=A1Δptanβiρi

(1)

其中

Fti=FpitanβiFpi=A1Δp

式中Ti——单个柱塞产生的理论瞬时转矩，N·m

Fti——导轨对单个柱塞的切向分力，N

Fpi——导轨对单个柱塞的径向分力，N

A1——内柱塞的作用面积，m2

βi——柱塞与导轨曲线的压力角，rad

Δp——内马达进出油口压差，Pa

ρi——柱塞对应导轨曲线的矢径，m

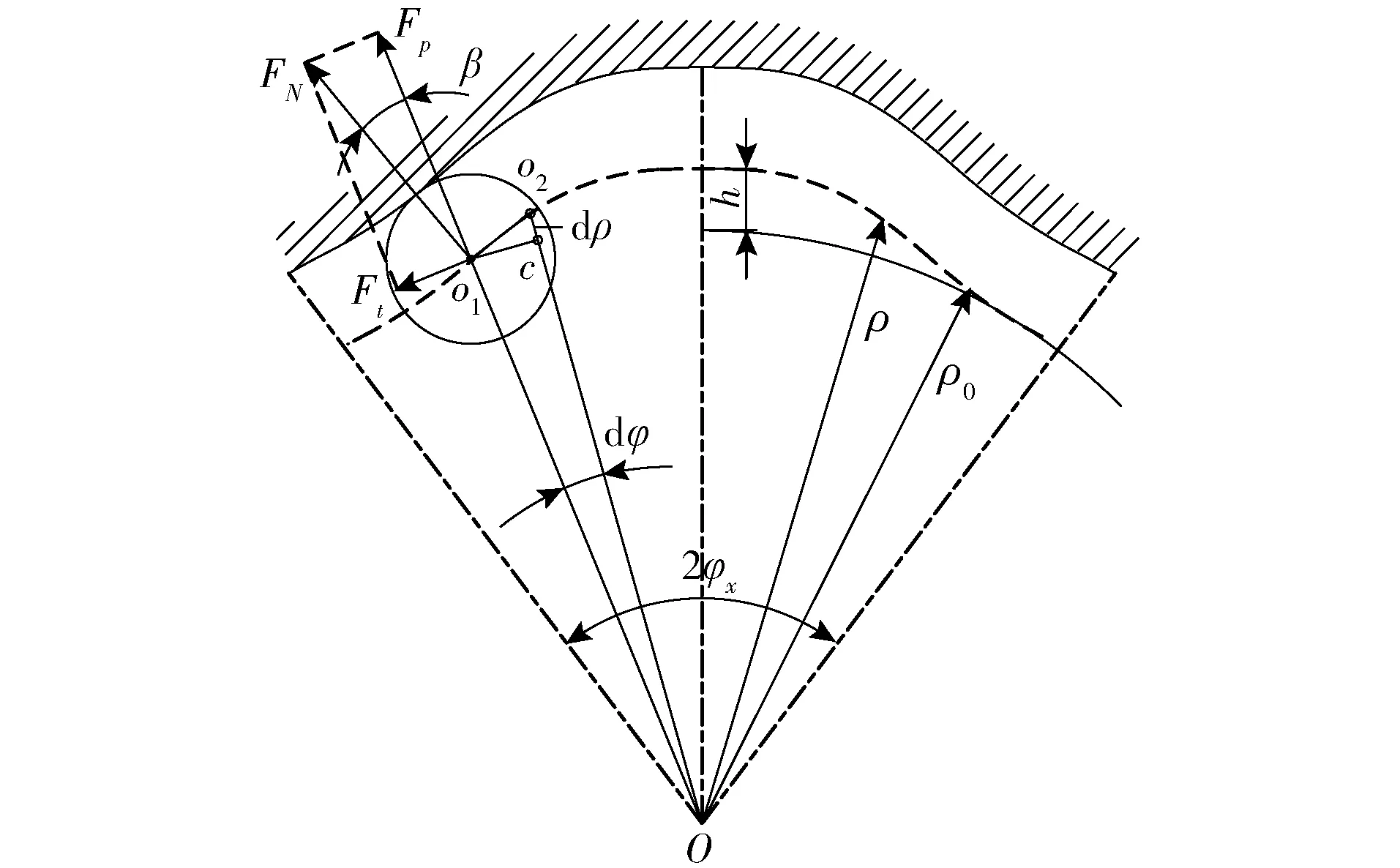
图2 柱塞在内导轨曲线的受力图Fig.2 Force diagram of plunger on inner rail curve

设柱塞转过dφ时的径向移动距离为dρ，如图2所示，△o1o2c为对应的微元三角形，o1c为dφ角度所对应的弧长，可得

(2)

式中vφi——导轨曲线的速度，m/rad

物理意义为柱塞转过一弧度时径向移动的距离

vφi=dρi/dφi

将式(2)代入式(1)可得

Ti=ΔpA1vφi

(3)

设内马达的柱塞总数为z，位于进油区段的柱塞数为z0，可得内马达的理论瞬时转矩为

(4)

2.1.2瞬时转速

设单个柱塞在dt内转过的角度为dφ，容积变化量为dv，由图2可得

dvi=A1dρi

单个柱塞的理论瞬时流量为

(5)

式中ω1——内马达的角速度，rad/s

将进油区段内各个柱塞的瞬时流量相加，得到内马达的理论瞬时流量

(6)

式中Qsh1——内马达的理论瞬时流量，m3/s

设输入马达的流量为q，则内马达的理论瞬时转速为

(7)

2.2 外马达单独工作

如图3所示，外马达输出转矩时，外柱塞与外导轨曲线相互作用，形成转矩。设外马达的柱塞在dt内转过的角度为dφ，在此过程中柱塞与缸体孔之间容积的变化量为dv，得外马达的理论瞬时流量为

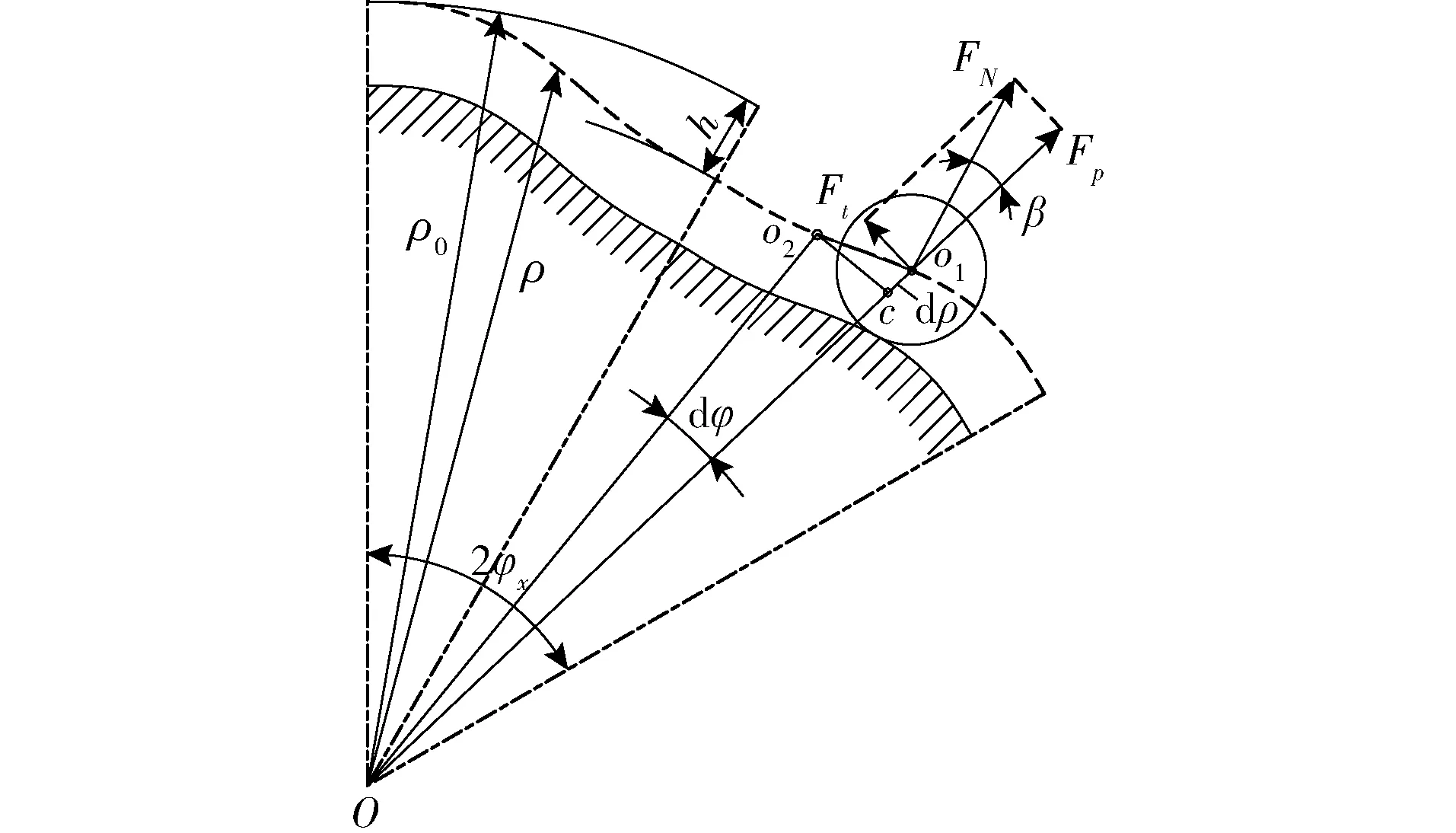
图3 柱塞在外导轨曲线的受力图Fig.3 Force diagram of plunger on outer rail curve

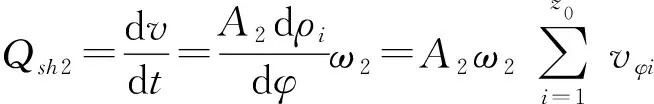
(8)

式中Qsh2——外马达的理论瞬时流量，m3/s

A2——外柱塞的作用面积，m2

ω2——外马达的角速度，rad/s

由式(8)可以得到，外马达的理论瞬时转矩和理论瞬时转速为

(9)

(10)

2.3 内、外马达共同工作

在内、外马达共同工作时，两个马达将输出合转矩，而两个马达的配流机构相互独立，故两个马达共同工作时的合瞬时转矩为内、外马达瞬时转矩的叠加。

Tsh3=Tsh1+Tsh2

(11)

内、外马达共用一个输出轴，故共同工作时的角速度相同，内、外马达共同工作时的理论瞬时排量为

(12)

式中Vsh3——内外马达共同工作时理论瞬时排量，m3/r

Vsh2——外马达的理论瞬时排量，m3/r

Vsh1——内马达的理论瞬时排量，m3/r

z1——内马达中位于进油区段内的柱塞数

z2——外马达中位于进油区段内的柱塞数

v1φi——内导轨曲线的速度，m/rad

v2φi——外导轨曲线的速度，m/rad

内、外马达共用工作时的理论瞬时转速为

(13)

3 马达输出转矩转速无脉动的条件

第2节推导了马达3种工作方式下的瞬时转矩和转速公式。在马达输入油液的压力和流量不变的情况下，马达的瞬时转矩与马达进油区内柱塞的速度之和有关。若马达进油区内柱塞的速度之和为常数，则马达的瞬时转矩不变，理论上马达不会出现转矩的波动；若马达进油区内柱塞的速度之和不为常数(基于导轨曲线的表达式一般呈周期函数的变化)，则马达的瞬时转矩会出现最大值和最小值，马达在运行过程中会出现转矩脉动。因此可以得出马达输出转矩无脉动的条件为

(14)

式中aφi——导轨曲线的加速度，m/rad2

马达进油区内柱塞的速度之和与导轨曲线和马达在进油区段内柱塞的分布位置有关。以6作用8柱塞的导轨曲线为例，分析柱塞在导轨曲线上的分布情况，如图4所示。图4b中的阴影部分表示进油区段，无阴影部分表示回油区段，柱塞均匀分布在导轨曲线上，两个柱塞之间的夹角为2π/z，导轨曲线的一个作用幅角为2φx。由图4可得，8个柱塞被平均分为两组，两组柱塞在导轨曲线上的相位对应相等。由图4b可知，柱塞在转过Δφ后，柱塞又回到在导轨曲线上的起始分布状态，可知每组柱塞在导轨曲线上的运动周期为Δφ，故马达进油区段柱塞的分布是以Δφ为周期变化的，马达的转矩脉动周期为Δφ。

图4 柱塞在导轨曲线的分布图Fig.4 Distribution plot of plunger on guide rail

设马达的作用数为x，柱塞数为z，作用数和柱

塞数的最大公约数为m，可以将柱塞分成相位对应相同的m个柱塞组，每组柱塞数为z′=z/m，得到马达的转矩脉动周期为

(15)

其中

φx=π/x

式中φx——导轨曲线的作用幅角，rad

由于每个柱塞组在导轨曲线上的分布情况和运动规律相同，只需研究一个柱塞组在进油区段内的速度和，而一组柱塞在进油区段内的柱塞数应为z′/2，故马达输出转矩无脉动的条件改写为

(16)

4 导轨曲线的转矩脉动分析

力偶型径向柱塞马达通过柱塞与凸轮环的作用输出转矩，凸轮环上的导轨曲线与马达的输出转矩有着直接的关系。该力偶型径向柱塞马达采用等加速-阿基米德螺旋线-等减速曲线，设等加速、等减速曲线的幅角分别为等速区φ0、等加速区φ1、等速区φ2、等减速区φ3，在一个作用区段内各个幅角的分配情况如图5所示。

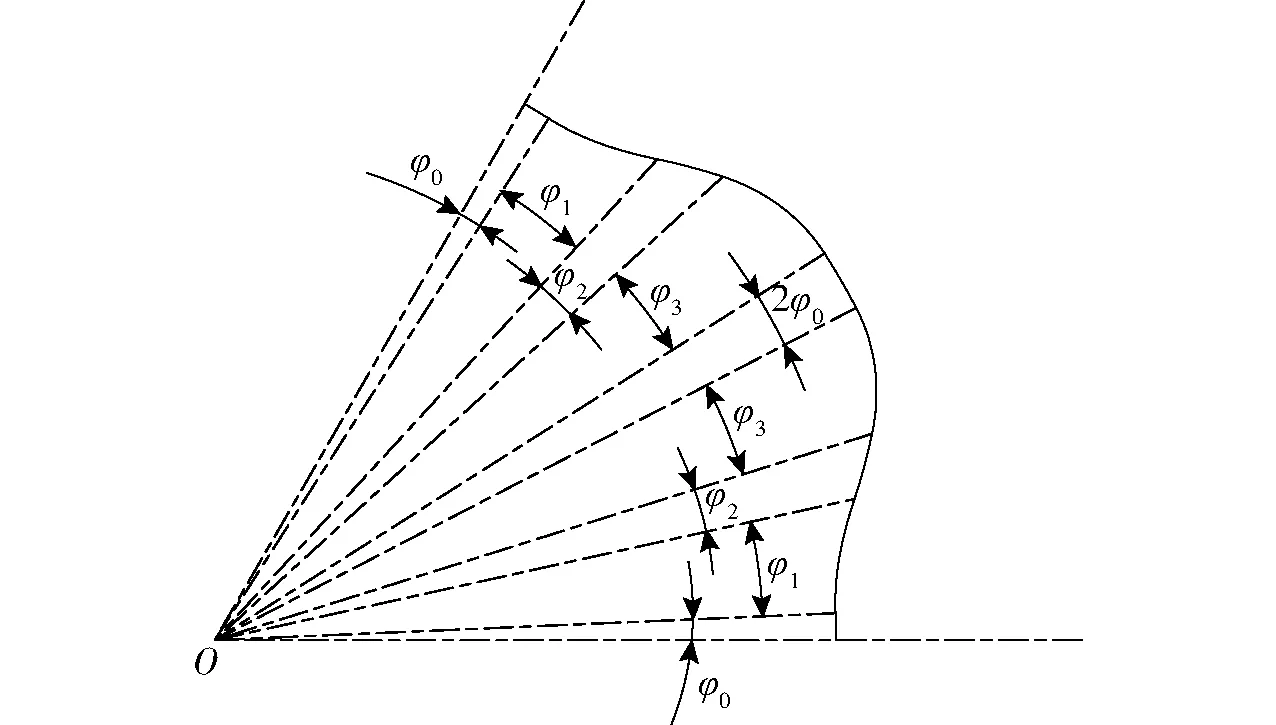
图5 等加速、等减速曲线在1个作用区段内各幅角的分配情况Fig.5 Distribution of angles of acceleration and other deceleration curves within one active zone

其方程式为

(17)

分析导轨曲线下的转矩脉动情况。曲线在等加速等减速区段内的加速度为常数。在加速区和减速区的加速度应满足

aφ1φ1+aφ3φ3=0

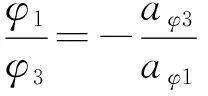
(18)

(19)

其中

aφ2=0

式中aφ1——导轨曲线等加速区的加速度,m/rad2

aφ2——导轨曲线等速区加速度,m/rad2

aφ3——导轨曲线等减速区的加速度,m/rad2

将式(18)代入式(19)，可得

(20)

因为aφ1≠0，所以

(21)

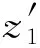
(22)

导轨曲线的一个作用幅角为

φx=2φ0+φ1+φ2+φ3

(23)

一个作用幅角内柱塞的分布情况为

(24)

令k=φx/Δφ，k2=(2φ0+φ2)/Δφ，则一组柱塞在进油区段内的分布情况为

k=k1+k2+k3

(25)

式中k——导轨曲线的总幅角分配系数

k1——导轨曲线等加速区幅角分配系数，为正整数

k2——导轨曲线等速区和零速区的幅角分配系数，为正整数或含有0.5的小数

k3——导轨曲线等减速区的幅角分配系数，为正整数

(26)

经过上述分析可知，等加速-阿基米德螺旋线-等减速曲线存在等速区，可以减少加速度突变时柱塞对导轨产生的冲击，零速区可以消除柱塞在切换高低压油时的困油现象，经过合理的角度分配可以实现理论上的无转矩转速脉动。本文采用理论上内、外马达无转矩转速脉动的幅角分配方案，内、外导轨曲线的幅角分配如表1所示。

表1 内、外导轨曲线的幅角分配情况Tab.1 Amplitude distribution condition of inner and outer rail curves (°)

5 马达的原理性实验

力偶型径向柱塞马达采用了新型结构形式，为了验证结构的合理性，在燕山大学流体传动与控制实验室搭建了马达实验台，实验现场见图6，测量马达在3种工作方式下的转矩转速特性。

图6 实验现场Fig.6 Test site photo

图7 实验液压系统原理图Fig.7 Test system diagram1、4、5、6.滤油器 2.温度计 3.液位计 7.变量泵 8.电机 9.单向阀 10、13、19、20.流量计 11、15、16压力表 12、14.溢流阀 17、18.三位四通电磁换向阀 21.力偶型径向柱塞马达 22.转矩转速测量仪 23.加载泵

设计了马达实验的液压系统，如图7所示。该系统可以切换3种马达工作方式，并且可以测量马达工作时的转矩、转速、流量、压力等各项参数。该实验系统通过三位四通换向阀切换马达的3种工作方式和正反转，工作方式的切换如表2所示。加载泵作为马达的负载，通过调节溢流阀的压力来控制负载的大小，转矩转速测量仪测量马达的输出转矩和转速。流量计10和压力表11测量液压泵的输出流量和压力，即为马达进油口的流量和压力，流量计13和压力表15测量马达回油口的流量和压力，流量计19和压力表16测量加载泵的流量和压力。

表2 马达工作方式对应电磁铁的通断电情况Tab.2 Working condition of motor corresponded to on-off condition of electromagnet

注：+表示通电；-表示断电。

本次实验对马达进行原理性实验，研究马达3种工作方式下的运行情况。考虑实验内容和成本，所加工的实验样机没有进行相关的热处理工序,本次实验中所选用的最高压力为6 MPa，设计内马达和外马达的理论排量分别为62、267 mL/r。在不同油液压力下测量马达3种工作方式的转矩转速，得到的实验曲线如图8所示。

6 结论

(1)在多作用内曲线径向柱塞马达的基础上提出了力偶型径向柱塞马达，该马达在一个壳体中可以形成内、外两个马达，分别有两种排量，内、外马达相互独立，通过配流方式的切换，可以实现内马达单独工作、外马达单独工作和内、外马达共同工作3种工作方式。马达的3种工作方式可以产生3种定排量，在相同的输入压力下可以输出3种定转矩和定转速，弥补了定量马达的不足，扩大了马达的应用范围。

图8 马达转矩转速实验数据Fig.8 Test data of motor torque and speed

(2)分析了马达导轨曲线与转矩转速脉动的关系，得出了马达3种工作方式下的瞬时转矩公式，公式表明，转矩转速脉动与进油区段柱塞的速度之和有关，若速度之和为常数，则无转矩转速脉动。分析了柱塞在导轨曲线的分布情况，得出转矩转速脉动为零时导轨曲线的幅角分配规律。

(3)搭建了马达实验台，对马达的输出特性进行实验及测量。内马达单独工作时输出转矩较低，转速较高；外马达单独工作时转矩较高，转速较低；内、外马达共同工作时输出最大转矩，最低转速。由数据可得，内、外马达共同工作时的转矩并不是内、外马达转矩的简单相加，而是小于内、外马达转矩之和，这主要是由于这种工作方式的摩擦副较多，机械损失较大。