基于可变集和云模型的河湖水系连通方案优选决策方法

冶运涛 梁犁丽 曹 引 蒋云钟 赵红莉 王建华

(中国水利水电科学研究院水资源研究所， 北京 100038)

0 引言

为应对我国水安全问题，2011年中央1号文件和水利部提出了河湖水系连通战略，但目前河湖水系连通的理论与技术研究尚在摸索阶段，远未形成指导生产实践的完整体系，不少学者对此开展了相关研究[1-2]。河湖水系连通研究目的就是通过分析河湖水系及连通工程特性，考虑到工程规划具有多目标、多层次等特征，立足于国家、区域、流域3个层面的国家战略需求，形成河湖水系连通在多个目标和多约束条件下的可行性方案集，然后建立方案集的资源、社会、经济、生态、环境、工程等多属性组成的指标体系，通过模拟计算和评估分析，优选确定河湖水系连通的规划方案[3]。

河湖水系连通工程(简称“连通工程”)方案优选是一个具有定性定量指标及模糊不确定信息的多目标多属性多层次的综合评价问题。建立一个能充分反映影响连通工程方案的社会经济、生态环境等各种因素的、科学系统的综合评价体系，并采用有效评价方法是方案优选的核心。常用的综合评价方法仍存在不足[4-9]，如人工神经网络法通过训练误差反馈反复修改网络权重，虽然一定程度上避免了评价者的主观影响，但往往导致花费时间多、收敛速度慢，且容易导致产生很多局部最小点；模糊综合评价法在评价过程中存在一定的不确定性，且模型难以自我调整与自我验证；灰色综合评价法在权重确定上过度依赖于不同级别的评价标准；集对分析和模糊集对分析分类方法在理论上存在基础性错误[10]。多数评价方法是将水资源系统评价对象作为模糊系统来处理，但影响它们的众多指标却是清晰的确定值，因此，水资源系统实质上是模糊清晰混合系统，需要新的评价原理与方法来对此进行评价。陈守煜[11]根据可变集辩证法基本规律数学原理，提出事物相对差异度演变定理，提出可变集模式识别矩阵，构建了水资源系统可变集评价原理与方法。

考虑连通工程优选评价各指标评价标准分级并没有明确的界限，具有模糊性，但是影响他们的众多指标却是清晰的确定值，因此河湖水系连通评价实质上是可变模糊清晰混合集，简称为可变集[11]。可变集是可变模糊集的发展，是对札德模糊集合论的突破，具有重要的理论意义[10]，已在多个领域得到应用[12-18]，并取得了很好效果，但是可变集在河湖水系连通工程方案优选中的适应性如何，尚未见文献报道；另外，现有文献将可变模型4种参数组合(可变模型中包括α和p参数，α为优化准则参数，取值为1和2分别相当于最小一乘方准则和最二乘方准则；p为距离参数，取值为1和2分别为海明距离和欧氏距离)计算结果的平均值作为最终评价结果，其合理性值得商榷。

针对上述问题，本文在已有成果基础上，首先，将对立统一、质量互变及否定之否定定理与河湖水系连通生产实践相结合，将“非此即彼”的清晰性指标与“亦此亦彼”的模糊概念辩证综合分析，提出基于可变集辩证法数学定理的科学、合理、快捷的河湖水系连通工程方案优选及排序方法；其次，为了客观评价不同参数组合的可变模型，分别以单一指标属性值变化和多个权重同时变化时采用不同参数组合的可变模型求得工程方案评价值作为样本数据，引入云模型进行灵敏度分析，对比可变模型决策结果的鲁棒性，帮助决策者选择决策结果鲁棒性更好的可变模型。最后，通过浙北引水工程算例分析，验证此方法在实际工程应用中的有效性和进行灵敏度分析的必要性。

1 河湖水系连通工程方案优选决策方法

基于可变集和云模型的河湖水系连通工程方案优选决策过程主要由两部分组成：①基于可变集的工程方案优选过程[11]。②基于云模型的工程方案评价灵敏度分析过程[19]。

1.1 基于可变集的工程方案优选过程

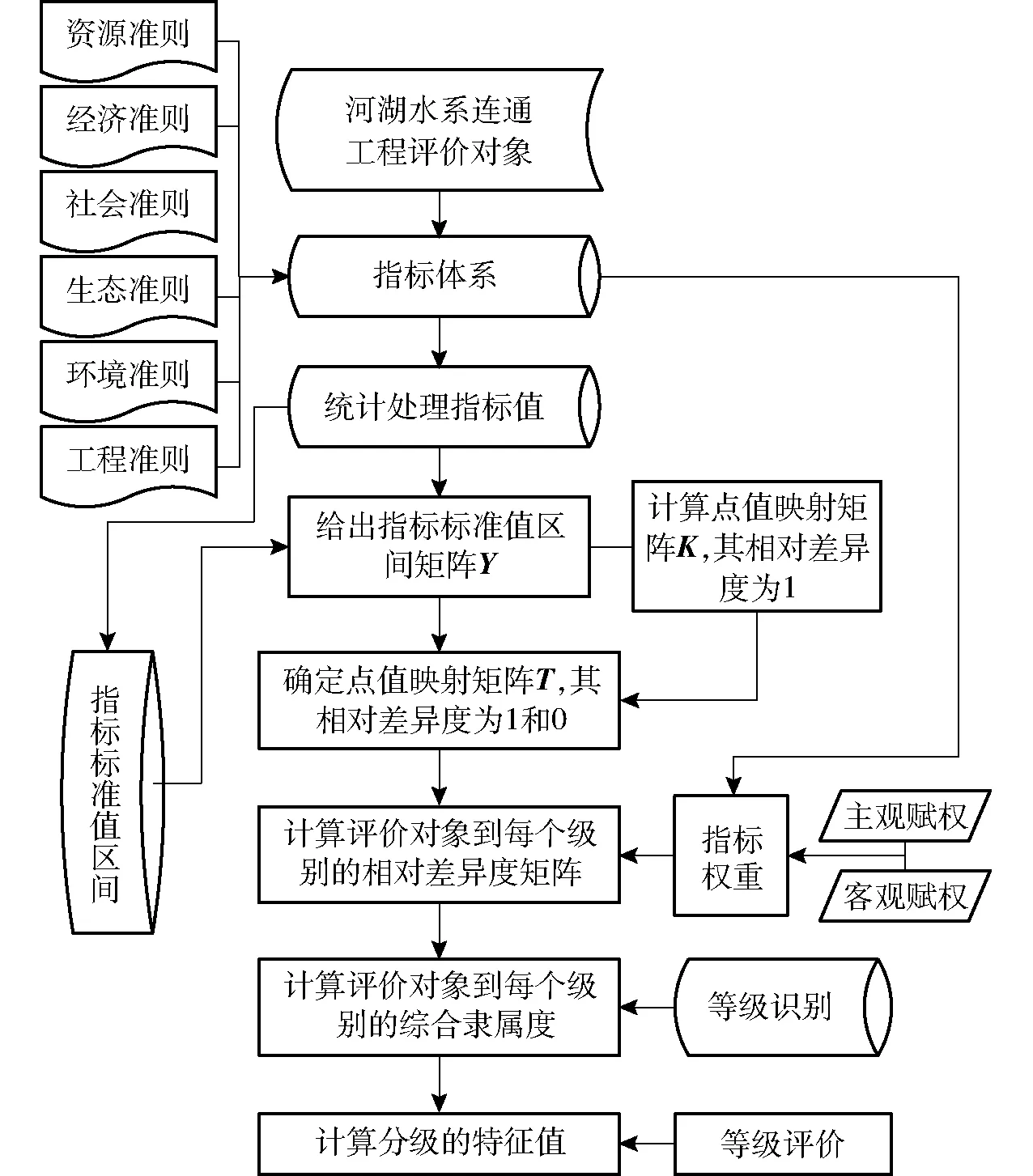
图1 基于可变集的工程方案优选过程流程图Fig.1 Flow chart for optimal selection process for project schemes based on variable set

可变集优选过程流程如图1所示。具体描述如下：

(1)确定河湖水系连通工程的评价对象。

(2)根据评价对象的特点，在实地调研、文献调研的基础上，依据资源、经济、社会、生态、环境、工程等准则，建立评价指标体系，并计算评价指标值。

(3)在指标值已经确定的情况下，根据评价者对指标体系中指标重要程度的认识，由主观、客观权重计算方法有机结合确定指标权重，既能体现人的经验判断，又能体现指标的客观特性。

(4)根据现有评价标准、实际情况或专家经验，确定不同等级下的指标标准值区间，进而给出指标标准值区间矩阵。

(5)计算点值映射矩阵K，其相对差异度为1，并确定点值映射矩阵T，其相对差异度为1和0。

(6)结合指标权重，计算评价对象到每个级别的相对差异度矩阵。

(7)计算评价对象到每个级别的综合隶属度，并计算分级的特征值，进行等级评价。

在此需要指出的是，本文研究重点是对可变集方法的应用特性分析，暂不涉及指标体系建立和指标权重确定研究。对河湖水系连通工程来讲，其评判准则分为资源、经济、社会、生态、环境、工程等，所有指标体系的分类均可归结到六大准则下。

决策过程步骤如下：

设河湖水系连通工程方案的好差分为c个级别。令h表示河湖水系连通工程方案级别变量，设h=1为好，h=2为较好,…,h=c为差。

设由n个河湖水系连通工程方案组成集合U，u为其中一个识别河湖水系连通工程方案对象，u∈U，以河湖水系连通工程评判指标i的特征值xi对u进行评判等级识别。已知的m个河湖水系连通工程方案评价指标c个级别的指标标准值区间矩阵为

Y=[aihbih](i=1,2,…,m;h=1,2,…,c)

(1)

其中，aih、bih分别为河湖水系连通工程评价指标i级h标准值上、下界。对于越小越优的河湖水系连通工程评价指标aihbih；相邻两级的河湖水系连通工程评价指标i标准区间值的交点bih，相当于对立统一与质量互变定理中h级向h+1级转化的渐变式质变点，即交点的相对隶属度μ(bih)=μ(ai(h+1))=0.5。由于存在渐变式质变点μ(bih)=0.5，根据对立统一定理，质变点两侧必存在两级(两极)对立，即h与h+1级构成对立级别，故A和A′可以分别以ih和i(h+1)替代。根据对立统一定理，对象u指标i对h与(h+1)级的相对隶属度之和为1，有

μih(u)+μi(h+1)(u)=1

(2)

计算式(2)中的μih(u)和μi(h+1)(u)，就可确定指标i级别h或h+1的相对隶属度，其方法如下：

(1)设1级(h=1)为好的河湖水系连通工程方案，根据标准值区间矩阵，评价指标i的1级标准值区间[ai1,bi1]的上界ai1对1级的相对隶属度为1，根据对立统一定理，则对对立级2级的相对隶属度为0，设ki1为对象u在区间[ai1,bi1]内对1级相对隶属度为1的点值，故ki1=ai1。

(2)设c级(h=c)为差的河湖水系连通工程方案，根据标准值区间矩阵，区间[aic,bic]的下界bic对c级的相对隶属度为1，对对立级(c-1)的下界bic对c级的相对隶属度为1，根据对立统一定理，对对立级(c-1)的相对隶属度为0，设kic为对应u在区间[aic,bic]内对c级相对隶属度为1的点值，故kic=bic。

(3)设h为2至(c-1)的中间级别，可取指标i级别h标准区间[aih,bih]的中点为h级相对隶属度为1的点值，即kih=(aih+bih)/2，则有

(3)

根据标准值区间矩阵Y与式(3)，可得指标相对隶属度为1的点值映射矩阵为

K=[kih]

(4)

根据式(4)与矩阵Y中的bih可得到相对隶属度为1和0.5所对应的点值映射矩阵为

T=[ki1bi1…bi(c-1)kic]m×(2c-1)
(i=1,2,…,m)

(5)

设已知河湖水系连通工程方案对象u的指标特征值矩阵为

X=[x1x2…xm]=[xi] (i=1,2,…,m)

(6)

设u的指标i特征值xi落入矩阵K中h与h+1级指标i的特征值相对差异度Dih(u)和Di(h+1)(u)等于1对应的点值区间[kih,ki(h+1)]内，区间内同时存在Dih(u)=0渐变式质变点bih，则xi对h和h+1级的相对差异度Dih(u)为

(7)

为计算方便，陈守煜[11]将相对差异度模型转变为相对隶属度模型，则指标特征值xij级别h相对隶属度模型为

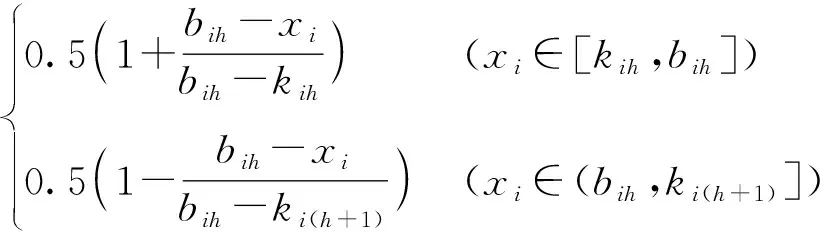
(8)

根据物理概念，对于小于h级、大于h+1级指标i的相对隶属度均应等于0，即

(9)

当xi落于模式识别矩阵T元素ki1与kic范围之外时，根据物理概念，对于越小越优指标，指标i对1级和c级的相对隶属度为

(10)

对于越大越优指标，指标i对1级和c级的相对隶属度为

(11)

式(5)、(6)是单指标相对差异度或隶属度的计算公式。由于评价是多指标识别，因此需要导出以指标相对差异表示的多指标综合相对隶属度非线性模型。

式(10)、(11)是单指标模型，而水资源评价是多指标综合评价问题。参考文献[11]，评价对象u的指标特征值xi对级别h的综合相对隶属度模型为

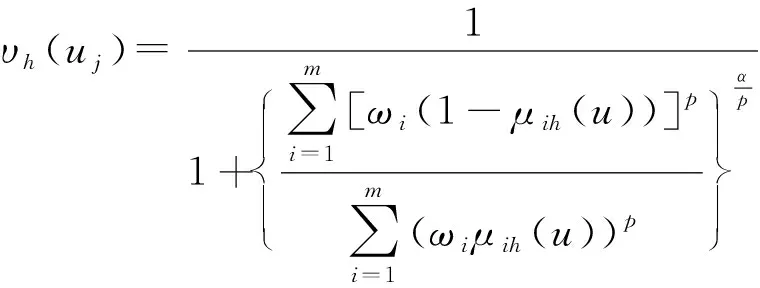
(12)

根据文献[11]可知，式(12)满足对立统一定理。式中α为优化准则函数，α=1相当于最小一乘方准则，α=2为最小二乘方准则，p为距离参数，p=1为海明距离，p=2为欧氏距离。当α=2时，无论采用p=1的海明距离，还是p=2的欧氏距离，式(12)都是非线性公式，对距离比值具有放大或缩小效应。不同参数组合下的计算模型，本文称之为可变模型。

根据式(12)可得评价对象u对各个级别的综合相对隶属度向量

υ(u)=(υ1，υ2，…，υc)=(υh(u))

(13)

应用文献[11]中的级别特征值公式

(14)

式中υh(u)——υh(u)的归一化向量

应用线性模型计算的向量值之和应等于1，即自动归一化，可用于计算校核之用。对每个评价对象u都进行类似计算，得到n个评价对象的级别特征值：H(u1)，H(u2)，…，H(un)，由此对评价对象逐一进行隶属等级的评定。

确定u的综合相对隶属度的计算公式为

(15)

根据式(7)可以计算u的相对差异度，根据质量互变定理可以进行方案的对比分析。

1.2 基于云模型的工程方案评价灵敏度分析过程

采用云模型理论对比可变集模型所得决策结果的数字特征期望Ex、熵En、超熵He以及云图重叠程度来分析其稳定性和随机性。首先利用逆向云发生器生成各自的云模型，其次通过正向云发生器生成云图，然后结合云模型和云图分析可变集模型的稳定性和随机性。具体生成算法见文献[14]。

1.2.1评价指标值灵敏度分析

工程方案评判指标值的不确定性将直接影响到决策结果的稳定性，分析其变化对决策结果的影响是整个灵敏度分析的基础。本文仅对单指标灵敏度进行分析，即每次只考虑一个指标值的变化，其他指标值不变，统计各备选方案排序变化情况，确定保持最优方案不变的取值区间。引入云模型理论进行单指标灵敏度分析，具体步骤如下：

(3)其他指标值不变，利用可变集模型计算备选工程方案的综合评价值。

(5)重复以上步骤，依次统计在其他指标值变化的整个取值区间各备选方案的综合评价值。

(6)以各备选方案在指标值变化情况下所得的综合评价值为样本数据，通过逆向云得到各备选方案的云模型(Ex,En,He)，然后生成云图，即可分析各备选方案在单个指标变化下排序结果的鲁棒性。

1.2.2评价指标权重灵敏度分析

除了指标值的变化，研究指标权重的变化对决策结果的影响也尤为重要。指标权重之和应等于1，假设所有备选方案的指标属性值不变。

多个权重同时变化灵敏度分析具体步骤如下：

(1)给ω1赋初值ω0，一般取ω0=0.01。

(2)用计算机生成1组随机权重ω2,ω3,…,ωj,…,ωy，满足权重之和为1-ω0，形成1组随机权重集合W1={ω0,ω2,ω3,…,ωj,…,ωy}。

(3)根据以上得到的随机权重集合，利用可变模型计算备选方案的综合评价值。

(4)改变ω1为ω1+ω0，然后重复以上步骤(2)～(3)，直到ω1=1，即可得到各备选方案综合评价值矩阵集合。

(5)利用同样的方法分别对ω2,ω3,…,ωj,…,ωy进行灵敏度分析。

(6)根据ω1,ω2,ω3,…,ωj,…,ωy的各备选综合评价值作为样本数据，计算其云模型，生成云图即可分析不同综合评价方法的决策结果的权重变化下的鲁棒性。

1.2.3基于云模型的工程方案灵敏度分析方法

对河湖水系连通工程方案决策结果在指标值和权重的整个取样空间进行灵敏度分析，首先通过指定各评判指标值或评判指标权重的变化范围，将可变集模型计算各备选方案评价值作为样本数据，通过1.2.1节和1.2.2节计算各备选方案的云模型参数，并生成对应的云图。

利用云模型参数和云图可以从以下两个方面分析工程方案决策结果的灵敏度：①在可变集模型评价法下横向对比各备选工程方案之间的排序稳定情况，首先根据方案的期望Ex排序，期望越大稳定性越好；若期望Ex相同，则熵En越小(即稳定性越好)排序稳定性越好，若期望Ex和熵En都相同，则超熵He越小(即随机性越小)排序稳定性越好。②当利用上述横向比较难以确定可变模型的鲁棒性时，进而根据云图纵向对比各可变模型之间决策结果的稳定情况，若最优方案的云分布与其他方案重叠越少，该方法得到的决策结果鲁棒性越好。

2 结果与分析

2.1 评价对象

浙北地区的水供需矛盾主要表现为嘉兴市水质型缺水、杭州市工程型缺水(局部资源型和水质型缺水)，且已成为制约该地区经济和社会可持续发展的瓶颈。为此浙江省发展和改革委员会组织了水利厅、建设厅、环保局以及有关科研设计单位，从综合性、宏观性的层面，开展了浙北引水工程前期研究工作，形成了《浙北引水工程前期研究报告》，拟定了新安江方案、富春江方案和太湖-富春江方案3个浙北引水方案，见表1。有关工程的详细参数参见文献[20]。

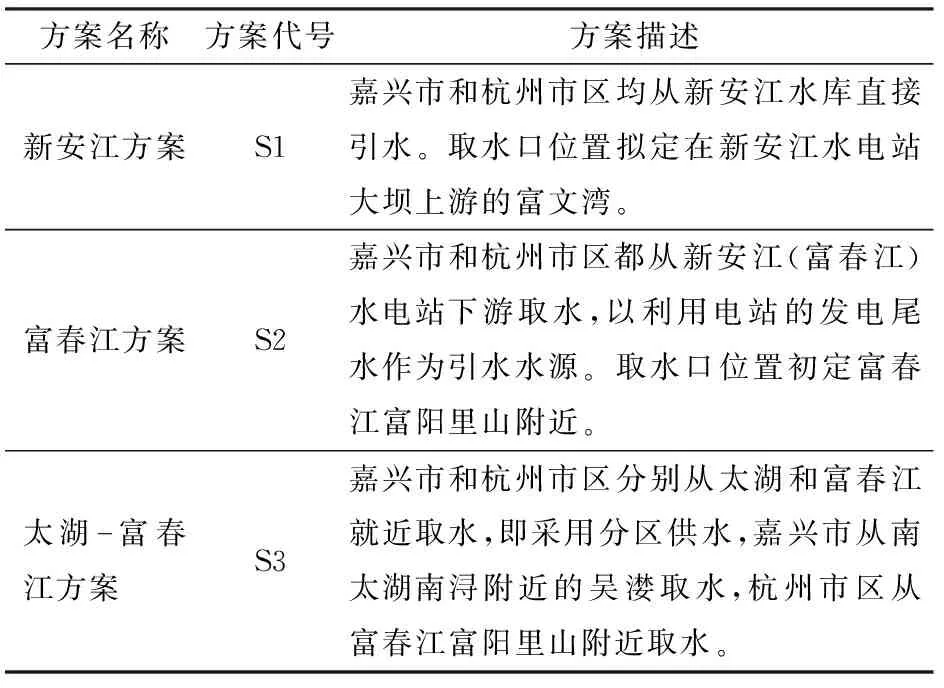
表1 备选工程方案Tab.1 Alternative project schemes

2.2 综合评价结果分析

根据文献[20]提供的指标值，将河湖水系连通工程评判指标的优劣程度分为5个级：1级(好)、2级(较好)、3级(一般)、4级(较差)、5级(差)。

根据参数α=1和p=1、参数α=1和p=2、参数α=2和p=1与参数α=2和p=2，利用上述组合的4种综合相对隶属度模型计算隶属度，再对隶属度值进行归一化，可以得到归一化的隶属度，计算结果见表2。其中相对差异度用RDD(Relative difference degree)表示，综合相对隶属度用CRMD (Comprehensive relative membership degree)表示，级别特征值用RFV(Rank feature value)表示。

从表2可看出，不同参数α和p的组合计算的同种方案的级别特征值不同。对S1方案，计算的级别特征值分别为3.10、3.10、2.84和2.65，前2种组合计算的方案处于3级和4级之间，接近3级；后2种组合计算的方案处于2级和3级之间，接近于3级；级别特征值从大向小转变，即等级低向等级高的方案转移。对S2方案，计算级别特征值分别为2.53、2.25、2.84和2.89，4种组合计算的特征值均处于2级和3级之间，级别特征值先从大到小，然后从小变大。对太湖-富春江S3方案，计算级别特征值分别为2.23、1.59、2.69和2.45，其中1种组合在1级和2级之间，另3种组合在2级和3级之间。

表2 各方案综合评价的RFV、RDD、CRMDTab.2 RFV, RDD and CRMD of comprehensive valuation for three project schemes

根据级别特征值，对相同参数的方案之间排序来看，前2种组合计算的方案由大到小排序：S3、S2、S1；第3种组合计算的方案由大到小排序：S3、S1、S2；第4种组合计算的方案是S3优于S1和S2，S1和S2没有差异。第1种组合计算的S1方案处于3级和4级之间，S2和S3方案处于2级和3级之间；第2种组合计算的S1方案处于3级和4级之间，S2方案处于2级和3级之间，S3方案处于1级和2级之间；第3种和第4种组合计算的S1、S2和S3方案均处于2级和3级之间，三者之间没有明显差别。

从不同参数组合来看，不同参数组合对3种方案的可辨识度不同。第1种组合，将S1和S2、S3方案区分出来，能够识别出较差方案；第2种组合，将S1、S2、S3方案区分出来；第3种和第4种组合，没有很好的识别度，S1、S2、S3方案基本处于同一类别，差别不是太大。

根据相对差异度分析，在前2种组合方案中，S1方案相对差异度均为-0.05，S2方案相对差异度分别为0.24和0.37，S3方案相对差异度分别为0.39和0.71；据相对差异度概念分析，新安江方案与其他两个方案具有质的区别，为不推荐方案，其他两个方案相比较，S3方案优于S2方案；不同的参数组合计算出的相对差异度不同，第2种组合计算的相对差异度值比第1种计算的差异度值要大，且相对差异度值增加的倍数也不一样，通过第2种组合相对差异度计算，可知S3方案为最优方案。

目前其他领域在使用可变集进行评价时，将4种参数组合的可变模型的计算均值作为最终评价结果。而本文实例证明，由于不同的可变模型计算出来的排序不一致，求其平均值就会导致不能细致区分优劣，这也说明多属性指标的模糊性导致了采用不同的可变模型计算评价结果的不确定性。据质量互变定理，相对差异度是衡量备选方案与理想值1的差异程度，结合相对差异度与可变模型中最大相对差异度与最小相对差异度的差值，可以选择可变模型(α=1，p=1)和(α=2，p=1)计算结果均值作为评价结果，或者直接选择可变模型(α=1，p=1)计算结果为评价结果。

通过结合级别特征值和相对差异度值评价结果合理性分析，并最终确定可变模型，克服了传统的单纯以4种模型计算均值作为评价结果的局限性。

2.3 不同准则的评价结果分析

本文2.2节是综合资源、经济、社会、环境和工程等各准则后的综合评估结果，但是没有反映出不同方案各准则的优劣分析。在实际工程案例中，可能不同决策者侧重的角度不同，需要分别对五大准则下的评价结果进行分析，以增进对工程的了解程度。表3为针对各准则计算的级别特征值、综合相对隶属度和相对差异度。下面分资源准则情景、经济准则情景、社会准则情景、环境准则情景和工程准则情景分别加以解析。

(1)资源准则情景

在4种参数组合情况下，S1和S2方案分别处于3级和4级之间，S3方案处于1级和2级之间，从相对差异度来看，S1方案的资源准则相对差异度DZ1、S2方案相对差异度DZ2、S3方案相对差异度DZ3满足以下关系：DZ1DZ2<0和DZ2DZ3<0，根据质量互变定理，S3方案和S1、S2方案有质的变化，明显优于S1方案和S2方案。

(2)经济准则情景

从相对差异度来看，S1方案的经济准则相对差异度DJ1、S2方案相对差异度DJ2、S3方案相对差异度DJ3满足以下关系：DJ1DJ2<0和DJ1DJ3<0，根据质量互变定理，S2、S3方案和S1方案有质的变化，两者明显优于S1方案。从参数组合情况来看，不同参数组合得到的结果略有差异，尤其表现在S2和S3方案的等级上，参数组合(α=1，p=1)和参数组合(α=1、p=2)情况下级别特征值S2方案小于S3方案，参数组合(α=2，p=1)和参数组合(α=2，p=2)情况下S3方案小于S2方案，但均表明S2方案和S3方案的等级较为接近，且明显高于S1方案。

表3 各方案基于不同准则评价的RFV、RDD、CRMDTab.3 RFV, RDD and CRMD of evaluations based on different criteria for three project schemes

(3)社会准则情景

从级别特征值看，参数组合(α=1，p=1)、(α=2，p=1)和(α=2，p=2)情况下，S1方案在2级和3级之间且偏3级，S2和S3方案在1级和2级之间且偏2级；参数组合(α=1，p=2)情况下，3个方案在2级和3级之间，S1方案距3级较近，S2和S3方案距2级较近。从相对差异度来看，4种参数组合计算的相对差异度值，S2和S3方案远大于S1方案，S2和S3方案相近。

(4)环境准则情景

从级别特征值来看，S1方案优于S2和S3方案；参数组合(α=1，p=1)和参数组合(α=1、p=2)情况下，S1方案接近2级，S2和S3方案略优于3级和略劣于3级，S2和S3方案接近；参数组合(α=2，p=1)和参数组合(α=2、p=2)情况下，S1方案优于2级，S2和S3方案均劣于3级，且两者较为接近。从相对差异度来看，4种参数组合计算均表明，S1方案优于S2和S3方案；参数组合(α=1，p=1)和参数组合(α=1、p=2)情况下，S1方案的相对差异度DH1、S2方案的相对差异度DH2、S3方案的相对差异度DH3的关系：DH1DH3<0，DH2DH3<0，说明S1和S2方案优于S3方案，DH2远大于DH3，说明S2方案优于S3方案，但S2方案接近于0，亦不是较优方案；参数组合(α=2，p=1)和参数组合(α=2、p=2)情况下，DH1DH3<0，DH1DH2<0，说明S1方案优于S2和S3方案，且有质的不同。

(5)工程准则情景

从级别特征值来看，4种参数组合下的S1方案在4级和5级之间，S2和S3方案在1级和2级之间，且两者较为接近；从相对差异度来看，4种参数组合下的S2和S3方案较为接近，均优于S1方案，S1方案的相对差异度DG1、S2方案的相对差异度DG2、S3方案的相对差异度DG3的关系为：DG1DG2<0，DG1DG3<0，说明S2和S3方案优于S1方案，且有质的变化。

2.4 指标灵敏度分析

2.4.1综合评价的指标灵敏度分析

为使4种可变模型计算各方案的决策结果更加直观，以指标变动下的方案综合评价值为样本数据，通过逆向云和正向云计算各方案的云模型(Ex,En,He)，结果如表4所示，生成的正态云图见图2。

从综合评价结果来看，可变模型(α=1,p=1)计算结果S3期望最优，S2方案次之，S1方案较差，3个方案的熵和超熵值接近，说明稳定性和随机性相差不大；可变模型(α=2,p=1)计算结果排序与可变模型(α=1,p=1)组合相似，但S2方案和S3方案的等级值有所提升，S1方案期望变化不大；可变模型(α=1,p=2)和(α=2,p=2)计算结果表明，S2方案期望最差，S1方案次之，S3方案最优。不同可变模型计算的排序有所变化。

从图2可看出，可变模型(α=1,p=1)计算结果表明，在单一指标变化情况下，S1方案的云图和S2、S3方案的没有重叠，说明S1方案是较差方案，S2和S3方案重叠较少，S3方案比S2方案优；可变模型(α=2,p=1)计算结果表明，S3方案和S1、S2方案的云图没有重叠，说明S3方案保持最优的稳定性没有改变，S2和S1方案云图重叠少，说明指标变化情况下，S2方案始终优于S1方案，S1方案是差方案。可变模型(α=1,p=2)计算结果表明，S1和S2方案重叠部分多，指标变化下，较易发生变化，S3方案和S1、S2方案云图也有所重叠，在指标变化情况下，排序也有可能发生变化；可变模型(α=2,p=2)

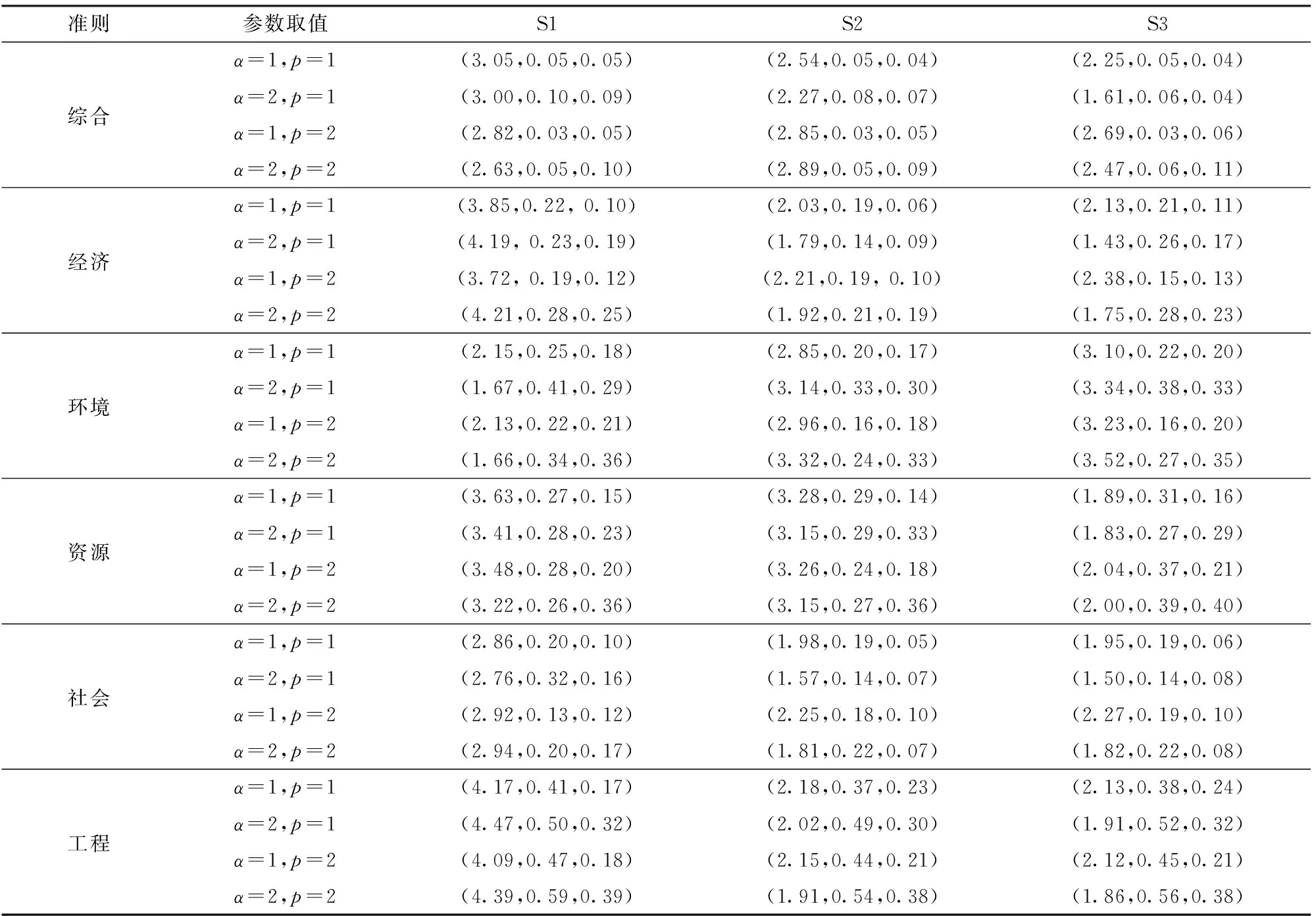
表4 指标变化下各方案评价值云模型参数Tab.4 Cloud model parameters of evaluation values under different index values

图2 指标变化下的各方案综合评价值云图Fig.2 Cloud images of comprehensive evaluation values under different index values

计算结果表明，S3和S1、S2方案均有多部分重叠，S2和S3方案排序较易发生变化。

综上分析可以得出，可变模型(α=1,p=1)和(α=2,p=1)计算3个工程方案的排序较稳定，应用在工程方案优选结果鲁棒性更好，其排序稳定性几乎不受单一指标值变化的影响。这也证明了传统的以4种可变模型计算平均值作为评价结果存在不足。

2.4.2不同准则评价的指标灵敏度分析

分析资源、经济、社会、环境和工程准则下的评价图的敏感性。

(1)资源准则评价值分析

如表4所示，在指标值发生变化下，4种可变模型计算结果，S3方案期望最高，S2方案期望略高于S1方案，对同一可变模型，3个方案的熵值和超熵值较为接近，说明同一参数组合计算结果的稳定性和随机性较为一致。从图3分析，S3方案云图和S1、S2方案重叠较少，说明S3方案维持最优方案的鲁棒性较强；S1和S2方案云图有所重叠，可变模型(α=2,p=2)参数组合下几乎完全重叠。

(2)经济准则评价值分析

如表4和图4分析，在指标值发生变化下，S2和S3方案的期望远高于S1方案，且这2个方案云图与S1方案重叠较少，说明S2和S3方案优于S1方案的排序鲁棒性强； S2和S3方案不同可变模型计算结果略有不同，可变模型(α=1,p=1)和(α=1,p=2)计算的S2方案期望略高于S3方案，而可变模型(α=2,p=1)和(α=2,p=2)的S3方案期望略高于S2方案，且2个方案不同可变模型计算结果云图的重叠度较高，说明这2个方案在指标变化下极易发生变化。

(3)社会准则评价值分析

如表4分析，在指标值发生变化下，S2和S3方案的期望远高于S1方案； S2和S3方案不同可变模型计算结果略有不同，但是级别特征值非常接近，不易区分2个方案的优劣。从图5分析，S2和S3方案云图和S1方案重叠较少，说明S2和S3方案优于S1方案的排序不易发生变化，但是S2和S3方案的云图几乎完全重叠，说明这2个方案在指标变化下排序极易发生变化。

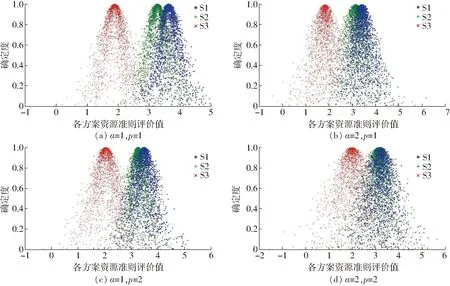
图3 指标变化下的各方案资源准则评价值云图Fig.3 Cloud images of evaluations based on resource criteria under different index values

图4 指标变化下的各方案经济准则评价值云图Fig.4 Cloud images of evaluations based on economical criteria under different index values

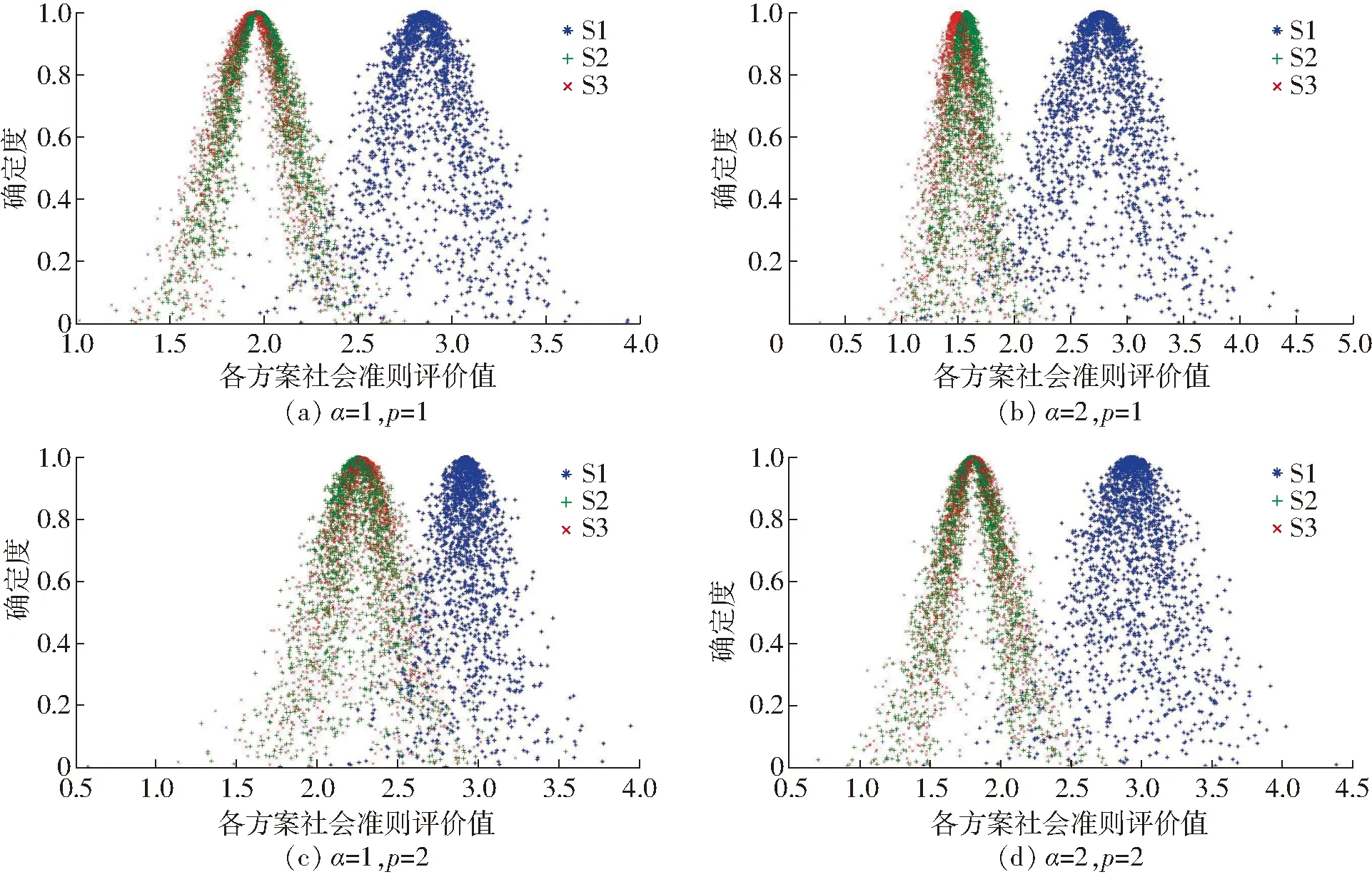
图5 指标变化下的各方案社会准则评价值云图Fig.5 Cloud images of evaluations based on social criteria under different index values

(4)环境准则评价值分析

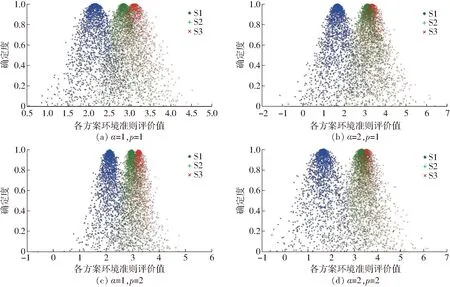
图6 指标变化下的各方案环境准则评价值云图Fig.6 Cloud images of evaluations based on environmental criteria under different index values

如表4分析，在指标值变化下，S1方案期望高于S2和S3方案，S2期望略高于S3方案；可变模型在α相同下，p=2与p=1相比，S1方案期望略有增高，S2和S3方案略有降低，但变化均不大；可变模型在p相同下，α=2与α=1相比，S1方案期望提升较多，S2和S3方案期望有所降低。从图6分析，S1方案维持排序稳定性要好于S2和S3方案，S2和S3方案云图重叠度高，说明这2个方案在指标变化下排序极易发生变化。

(5)工程准则评价值分析

如表4分析，在指标值发生变化下， S2和S3方案期望高于S1方案，S3期望略高于S2方案。如图7所示，S2、S3方案和S1方案重叠较少，说明这2个方案优于S1方案的排序稳定性强；S2和S3方案重叠度高，这说明指标变化下，S2和S3方案的排序极易发生变化。

2.5 权重灵敏度分析

2.5.1综合评价的权重灵敏度分析

分别在4种参数组合下，以指标权重变动下的方案综合评价值为样本数据，通过逆向云和正向云计算各方案的云模型(Ex,En,He)，结果如表5所示。

从综合评价结果来看，可变模型(α=2,p=2)计算的熵值大于样本方差均方根值，说明该模型计算结果在指标权重变化下的稳定性非常差，不宜用作方案评价；可变模型(α=1,p=1)、(α=2,p=1)和(α=1,p=2)计算的S3期望最优，S2方案次之，S1方案较差，其中S2和S3方案级别特征值相差不大，且各方案的熵值和超熵值较为接近，说明稳定性和随机性程度比较接近。

图7 指标变化下的各方案工程准则评价值云图Fig.7 Cloud images of evaluations based on engineering criteria under different index values

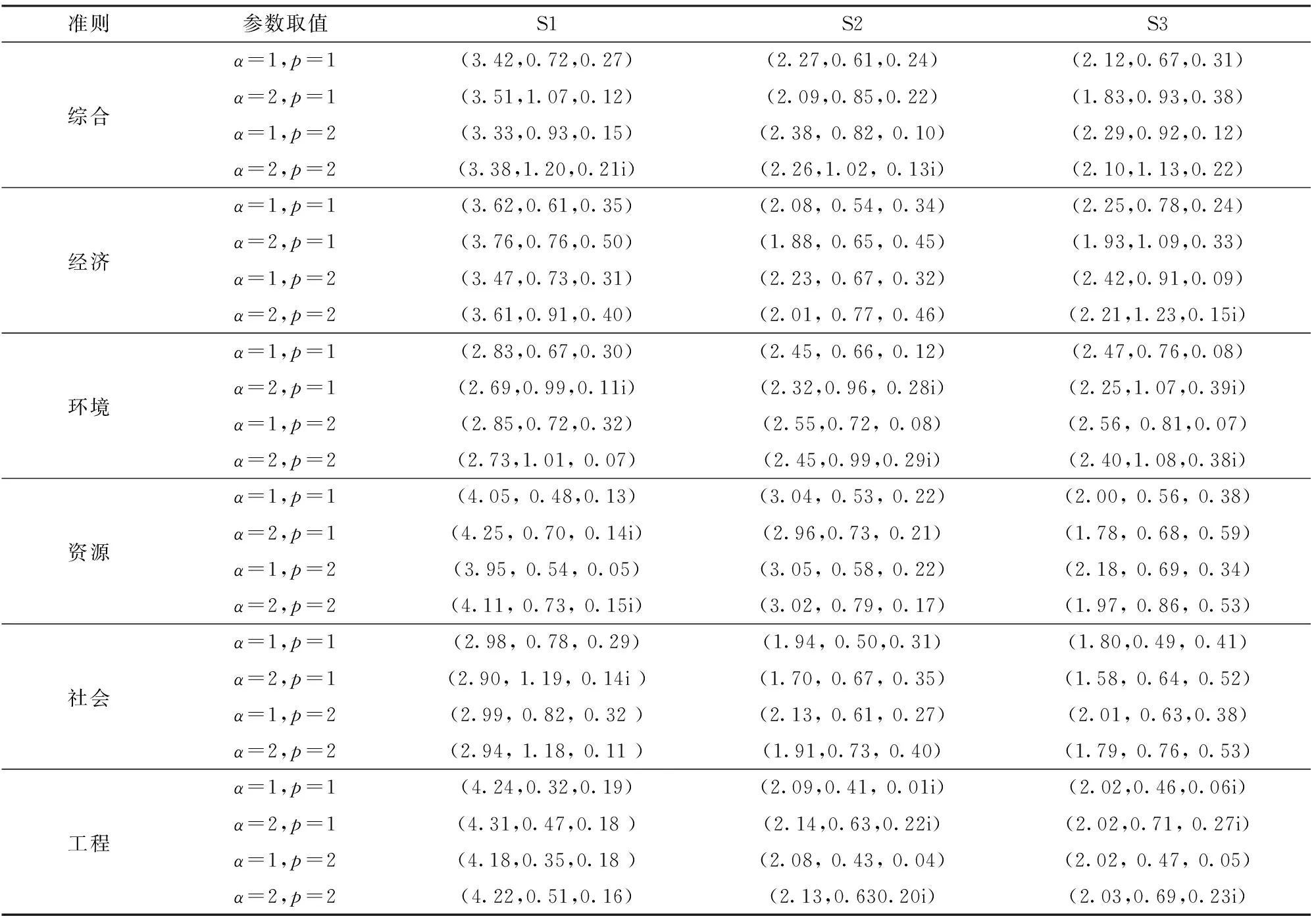
准则参数取值S1S2S3α=1,p=1(3.42,0.72,0.27)(2.27,0.61,0.24)(2.12,0.67,0.31)综合α=2,p=1(3.51,1.07,0.12)(2.09,0.85,0.22)(1.83,0.93,0.38)α=1,p=2(3.33,0.93,0.15)(2.38, 0.82, 0.10)(2.29,0.92,0.12)α=2,p=2(3.38,1.20,0.21i)(2.26,1.02, 0.13i)(2.10,1.13,0.22)α=1,p=1(3.62,0.61,0.35)(2.08, 0.54, 0.34)(2.25,0.78,0.24)经济α=2,p=1(3.76,0.76,0.50)(1.88, 0.65, 0.45)(1.93,1.09,0.33)α=1,p=2(3.47,0.73,0.31)(2.23, 0.67, 0.32)(2.42,0.91,0.09)α=2,p=2(3.61,0.91,0.40)(2.01, 0.77, 0.46)(2.21,1.23,0.15i)α=1,p=1(2.83,0.67,0.30)(2.45, 0.66, 0.12)(2.47,0.76,0.08)环境α=2,p=1(2.69,0.99,0.11i)(2.32,0.96, 0.28i)(2.25,1.07,0.39i)α=1,p=2(2.85,0.72,0.32)(2.55,0.72, 0.08)(2.56, 0.81,0.07)α=2,p=2(2.73,1.01, 0.07)(2.45,0.99,0.29i)(2.40,1.08,0.38i)α=1,p=1(4.05, 0.48,0.13)(3.04, 0.53, 0.22)(2.00, 0.56, 0.38)资源α=2,p=1(4.25, 0.70, 0.14i)(2.96,0.73, 0.21)(1.78, 0.68, 0.59)α=1,p=2(3.95, 0.54, 0.05)(3.05, 0.58, 0.22)(2.18, 0.69, 0.34)α=2,p=2(4.11, 0.73, 0.15i)(3.02, 0.79, 0.17)(1.97, 0.86, 0.53)α=1,p=1(2.98, 0.78, 0.29)(1.94, 0.50,0.31)(1.80,0.49, 0.41)社会α=2,p=1(2.90, 1.19, 0.14i )(1.70, 0.67, 0.35)(1.58, 0.64, 0.52)α=1,p=2(2.99, 0.82, 0.32 )(2.13, 0.61, 0.27)(2.01, 0.63,0.38)α=2,p=2(2.94, 1.18, 0.11 )(1.91,0.73, 0.40)(1.79, 0.76, 0.53)α=1,p=1(4.24,0.32,0.19)(2.09,0.41, 0.01i)(2.02,0.46,0.06i)工程α=2,p=1(4.31,0.47,0.18 )(2.14,0.63,0.22i)(2.02,0.71, 0.27i)α=1,p=2(4.18,0.35,0.18 )(2.08, 0.43, 0.04)(2.02, 0.47, 0.05)α=2,p=2(4.22,0.51,0.16)(2.13,0.630.20i)(2.03,0.69,0.23i)

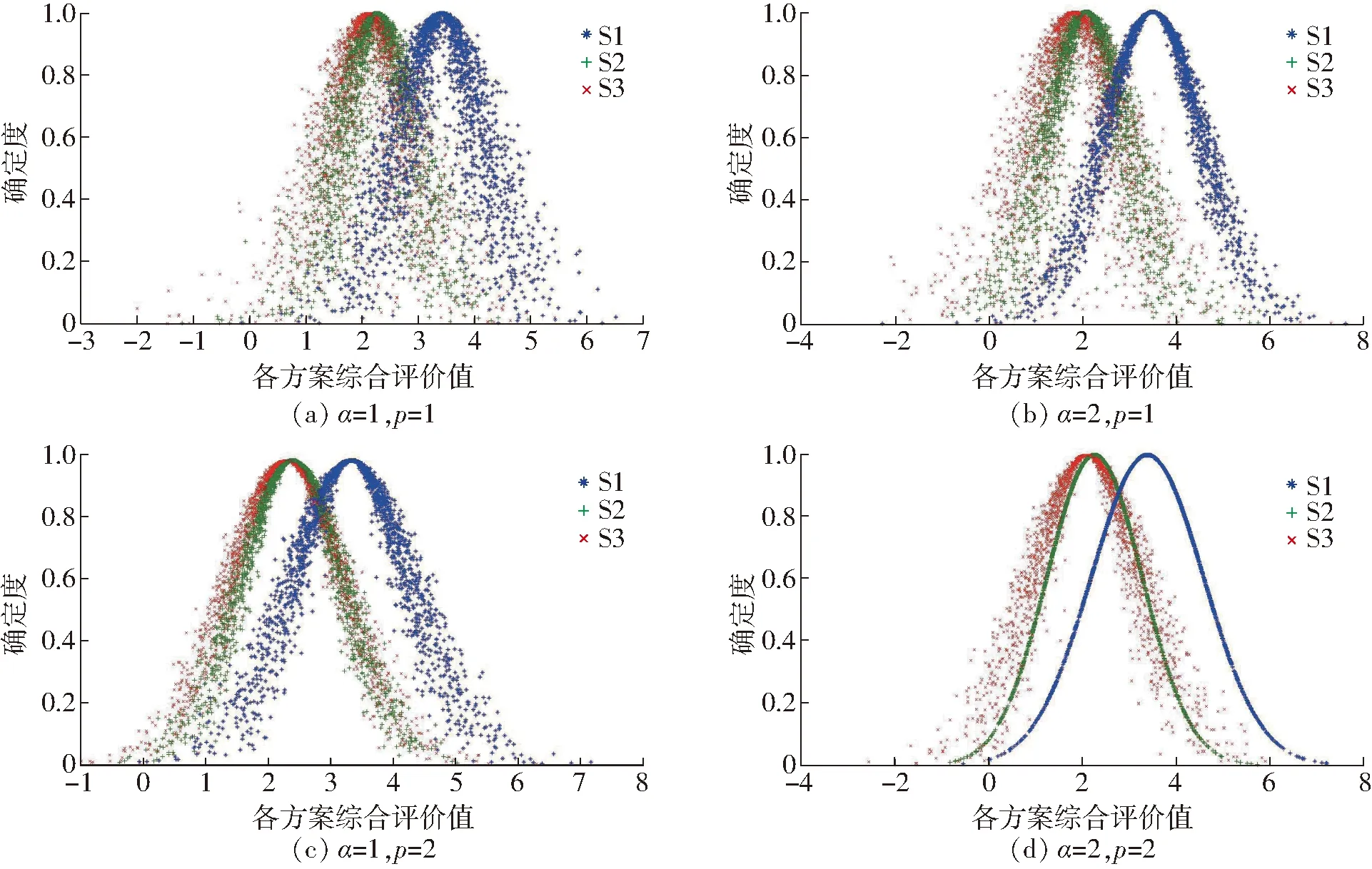
图8 指标权重变化下的各方案综合评价值云图Fig.8 Cloud images of comprehensive evaluation values under different index weights

从图8可看出，S2和S3方案的云图重叠较多，说明在指标权重变化下，2个方案的排序较易发生变化；S1方案和S2、S3方案云图也有重叠，说明这3种方案的情景下，S1方案和S2、S3方案也有可能发生变化。与可变模型(α=1,p=1)相比，可变模型(α=2,p=1)和(α=1,p=2)计算结果随机性不强，且各自维持稳定性的性质较好。

2.5.2不同准则评价的权重灵敏度分析

分析资源、经济、社会、环境和工程准则下的评价图的敏感性。

(1)指标权重变化下的资源准则评价值分析

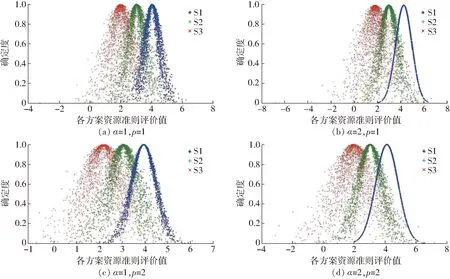
图9 指标权重变化下的各方案资源准则评价值云图Fig.9 Cloud images of evaluations based on resource criteria under different index weights

从表5可看出，在指标权重变化下，可变模型(α=2,p=1)和(α=2,p=2)灵敏度高，导致计算结果不合理。可变模型(α=1,p=1)和(α=1,p=2)计算的S3方案期望最高，S2方案次之，S1方案期望最低。从图9可看出，3个方案云图均有重叠，说明在指标权重变化下，3个方案的排序也会发生变化。

(2)指标权重变化下的经济准则评价值分析

从表5可看出，在指标权重变化下，可变模型(α=2,p=2)灵敏度高，导致计算结果不合理。可变模型(α=1,p=1)、(α=2,p=1)和(α=1,p=2)计算的S2方案期望最高，S3方案次之，S1方案期望最低，S2方案期望略高于S3方案。从云图10可看出，3个云图方案均有重叠，说明在指标权重变化下，3个方案的排序也会发生变化，其中S2方案和S3方案重叠度高，排序更易发生变化。

(3)指标权重变化下的社会准则评价值分析

图10 指标权重变化下的各方案经济准则评价值云图Fig.10 Cloud images of evaluations based on economic criteria under different index weights

图11 指标权重变化下的各方案社会准则评价值云图Fig.11 Cloud images of evaluations based on social criteria under different index weights

从表5可看出，在指标权重变化下，可变模型(α=2,p=1)灵敏度高，导致计算结果不合理。可变模型(α=1,p=1)、(α=1,p=2)和(α=2,p=2)计算的S3方案期望最高，S2方案次之，S1方案期望最低，S3方案期望略高于S2方案。从图11可看出，3个云图方案均有重叠，说明在指标权重变化下，3个方案的排序也会发生变化，其中S2方案和S3方案重叠度高，排序更易发生变化。

(4)指标权重变化下的环境准则评价值分析

从表5可看出，在指标权重变化下，可变模型(α=2,p=1)和(α=2,p=2)灵敏度高，导致计算结果不合理。可变模型(α=1,p=1)和(α=1,p=2)计算的S3和S2方案期望非常接近，均高于S1方案。从图12可看出，3个云图方案均有重叠，说明在指标权重变化下，3个方案的排序也会发生变化。

(5)指标权重变化下的工程准则评价值分析

从表5可看出，在指标权重变化下，可变模型(α=1,p=1)、(α=2,p=1)和(α=2,p=2)灵敏度高，导致计算结果不合理。可变模型(α=1,p=2)计算的S3和S2方案期望非常接近，均高于S1方案。从图13可看出，S2和S3方案云图和S1方案几乎没有重叠，说明S2和S3方案优于S1方案的排序稳定性强；S2和S3方案云图重叠度高，说明这2个方案排序极易发生变化。

图12 指标权重变化下的各方案环境准则评价值云图Fig.12 Cloud images of evaluations based on environmental criteria under different index weights

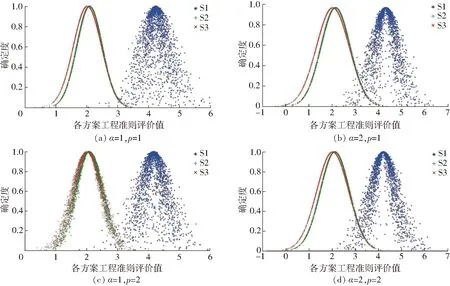
图13 指标权重变化下的各方案工程准则评价值云图Fig.13 Cloud images of evaluations based on engineering criteria under different index weights

3 结论

(1)提出河湖水系连通工程方案优选决策的可变集原理与方法以及基于云模型的指标值和指标权重灵敏度分析方法。以浙北引水工程的新安江、富春江和太湖-富春江等3种方案为研究对象，综合评价和分资源、经济、社会、环境、工程准则评价了3种方案排序，并基于云模型进行了灵敏度分析。

(2)利用不同(α,p)参数的可变模型，综合评价了S1、S2和S3等3种方案。采用级别特征值和相对差异度相结合的方法进行分析，得出S3是最优方案，且说明了S1和S2、S3具有质的不同。同时，分准则评价了S1、S2和S3等3种方案；从评价结果来看，对同一准则评价，4种可变模型的评价等级有一定差别，但是对3种方案的排序呈现相似性；在资源准则评价方面，S3最优，S1和S2差异不大；在环境准则评价方面，S1最优，S2和S3差异不大；在其他准则评价方面，S2和S3均优于S1，且S2和S3差异不大。

(3)在指标变化情况下，在综合评价方面，可变模型(α=1,p=1)和(α=2,p=1)的评价云图重叠性不大，说明3种方案的排序受指标变化影响不大，而可变模型(α=1,p=2)和(α=2,p=2)的评价云图重叠性较大，说明3种方案排序容易发生变化。在分准则评价方面，同一准则的4种可变模型的评价云图具有相似性：资源准则评价云图中，S3和S1、S2重叠较少，S1和S2重叠较多；环境准则评价云图中，S1和S2、S3重叠少，S2和S3重叠多；在经济、社会、工程等准则评价云图中，S2、S3和S1重叠少，S2和S3重叠多。云图重叠多，说明方案排序易受指标变化的影响，反之，则影响较少。从上述结果来看，不同指标集对评价结果具有一定的影响。

(4)在指标权重变化情况下，在综合评价方面，4种参数组合的可变模型评价的云图均有重叠，且S2和S3重叠度高，说明方案排序易受指标权重的影响。在不同准则评价方面，工程准则评价云图中，S1和S2、S3几乎没有重叠，说明S1在工程方面劣于S2和S3；此外，其他准则评价的云图均有重叠，且S2和S3方案重叠度高，说明这些准则的排序评价易受指标权重的影响。

(5)结合综合评价和不同准则评价的指标灵敏度和指标权重灵敏度分析来看，指标体系对评价结果有一定的影响，这说明该方法需要结合不同的研究对象进行具体分析，选择合适的评价方法。因此，今后还应把建立的方法应用更多算例来验证，总结出普适性规律，深入论证此方法的有效性。