一种估算粘性土抗剪强度参数的统计模型

李 云



一种估算粘性土抗剪强度参数的统计模型

李 云

（四川南充水利电力建筑勘察设计研究院，四川 南充 637000）

土体力学性质与其基本物理性质密切相关。通常力学指标测试程序繁琐，耗时长，而物理指标测试相对简单、快捷。建立土体物理指标与力学指标的定量关系是土力学的基本任务之一。通过对粘性土基本物理指标和抗剪强度参数的单因素回归分析，以相关系数R≥0.4作为指标相关性的初选标准，进一步进行多元回归分析，最终建立了具有统计意义的一种基于粘性土基本物理指标估算其抗剪强度参数的统计模型。经具体工程实例对该模型的检验表明所建立的统计模型具有实际应用前景。

粘性土；物理指标；抗剪强度参数；统计模型

土体的抗剪强度参数（即内摩擦角￠和凝聚力C）是土体非常重要的力学参数，广泛运用于地基承载力计算、深基坑支护计算和边坡抗滑稳定计算等工程实践中。该参数选用的适当与否直接关系到建设工程的投资与安全，偏保守时会极大地增加工程投资，造成不必要的浪费；而偏冒进则会使建筑物的安全受到极大威胁，进而威胁到人民群众的生命安全和财产安全。因此，正确选择土体的抗剪强度参数是岩土工作者的一项重要基础工作。岩土工作者选择土体抗剪强度参数的途径不外乎两种，一种是依据经验进行选择，另外一种是依据试验报告进行选择。经验来源于实践，没有丰富的工程实践经验，要想进行正确的选择是比较困难的。当根据试验报告进行选择时同样面临着一种风险，即试验报告中试样等级是否满足要求的风险。用于测试粘性土抗剪强度参数的土样必须是Ⅰ级试样[1]。现在很多勘察单位受市场环境、市场因素的影响，往往忽视或不重视土样样品的质量，采集的样品因为受采样方式或运输的影响，很难保证样品的质量要求。在样品等级达不到要求的情况下所测试的抗剪强度参数是不具备使用价值的。基于上述原因建立一种能基于土体基本物理指标反映土体抗剪强度参数的模型是很有必要的，一方面土体基本物理指标测试所需样品的质量等级要求不是很高[1]，基本上所有勘察单位采集的样品都可满足要求，提高的样品的可用度和可信度；另一方面，物理指标测试历时较短，测试方法相对简单、容易，能快速出结果，可以满足项目进度要求；再者，使用精度较高的模型对岩土工作者来说可避免犯一些经验主义的错误，更为实践经验不太丰富的青年岩土工作者提供了一种正确选用强度参数的依据。

1 土体抗剪强度参数的影响因素

土的抗剪强度虽为土本身所具有，但其他众多因素也有影响。从土体本身来讲，其矿物成分、粒度成分、结构连接及排列方式、密度、饱和度、土及水中可交换离子成分及含量都影响土的抗剪强度参数值的大小。另一方面，土的强度与受荷条件有关，而且土的抗剪强度参数值的大小还与粘性土的受荷固结条件和历史有关[2]。

就某一个地区对同一种土类来说，其形成历史、受荷条件是相同的，土中的矿物成分、结构连接方式、土及水中可交换离子成分及含量也是基本相同的，因此，影响土体抗剪强度参数的主要因素应归结于土的粒度成分、含水量和密度等。

一直以来，不少学者都研究、探讨过土的物理性质与抗剪强度参数之间的关系。卢肇均院士1962年就研究过软土内摩擦角和塑性指数之间的关系[3]，他得到的表达式为：￠=43°-0.92Ip（7＜Ip＜18），该线性表达式的相关系数r=-0.665。1991年其发表的粘性土基本内摩擦角与塑性指数的关系[4]为：

当7≤Ip＜55时，￠0=37.4°-0.49Ip；

当Ip≥55时，￠0=12.4°-0.0427Ip；

卢肇均院士的上述成果均是建立在扰动制样基础上的研究成果，没有考虑土体本身的结构性，或者说研究者更多地是从填方路基的工程实际出发考虑土体重塑后的抗剪强度参数。

2 粘性土基本物理指标与抗剪强度参数的单因素相关性

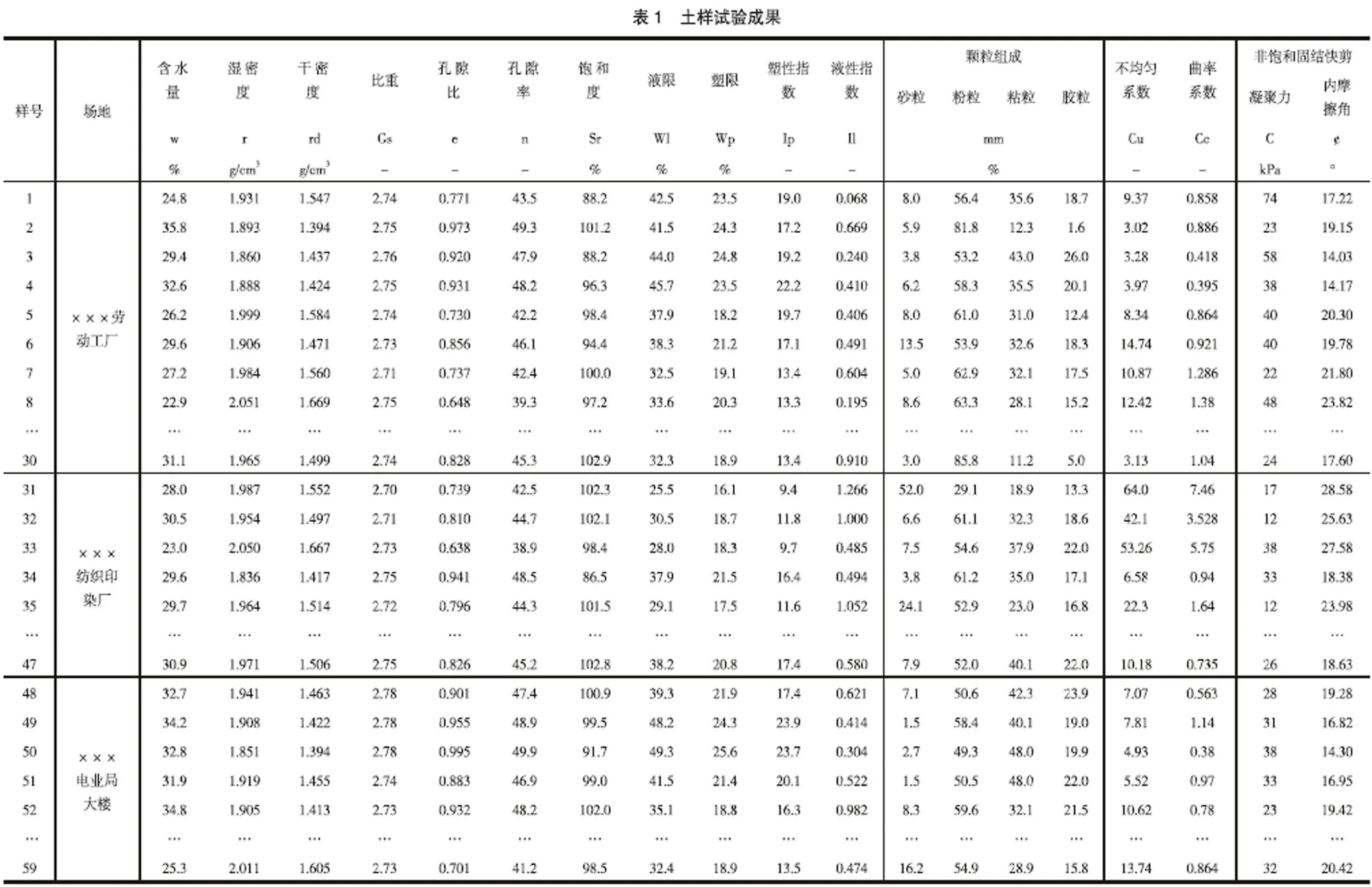
选用的研究样本的基本数据列于表1[5]。研究样本来源于三个场地。该三个场地在平面上彼此呈三角形，场地间直线距离10~40km，三个场地的粘性土成因均为冲积成因。利用EXCEL将土的各物理指标分别与其内摩擦角和凝聚力进行单因素拟合回归分析，拟合回归结果列于表2。

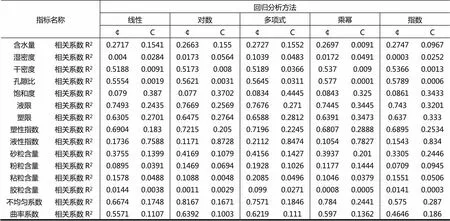
表2 物理指标与抗剪强度参数单因数回归分析结果

如果将相关系数R2≥0.15作为判别标准，从表2的分析结果可以看出粘性土内摩擦角的影响因素从大到小依次为：不均匀系数、液限、塑性指数、塑限、曲率系数、孔隙比、干密度、砂粒含量、含水量、液性指数、粘粒含量等十一个物理指标。粘性土凝聚力的影响因素从大到小依次为：液性指数、饱和度、液限、塑限、塑性指数、不均匀系数、含水量、砂粒含量等八个物理指标。

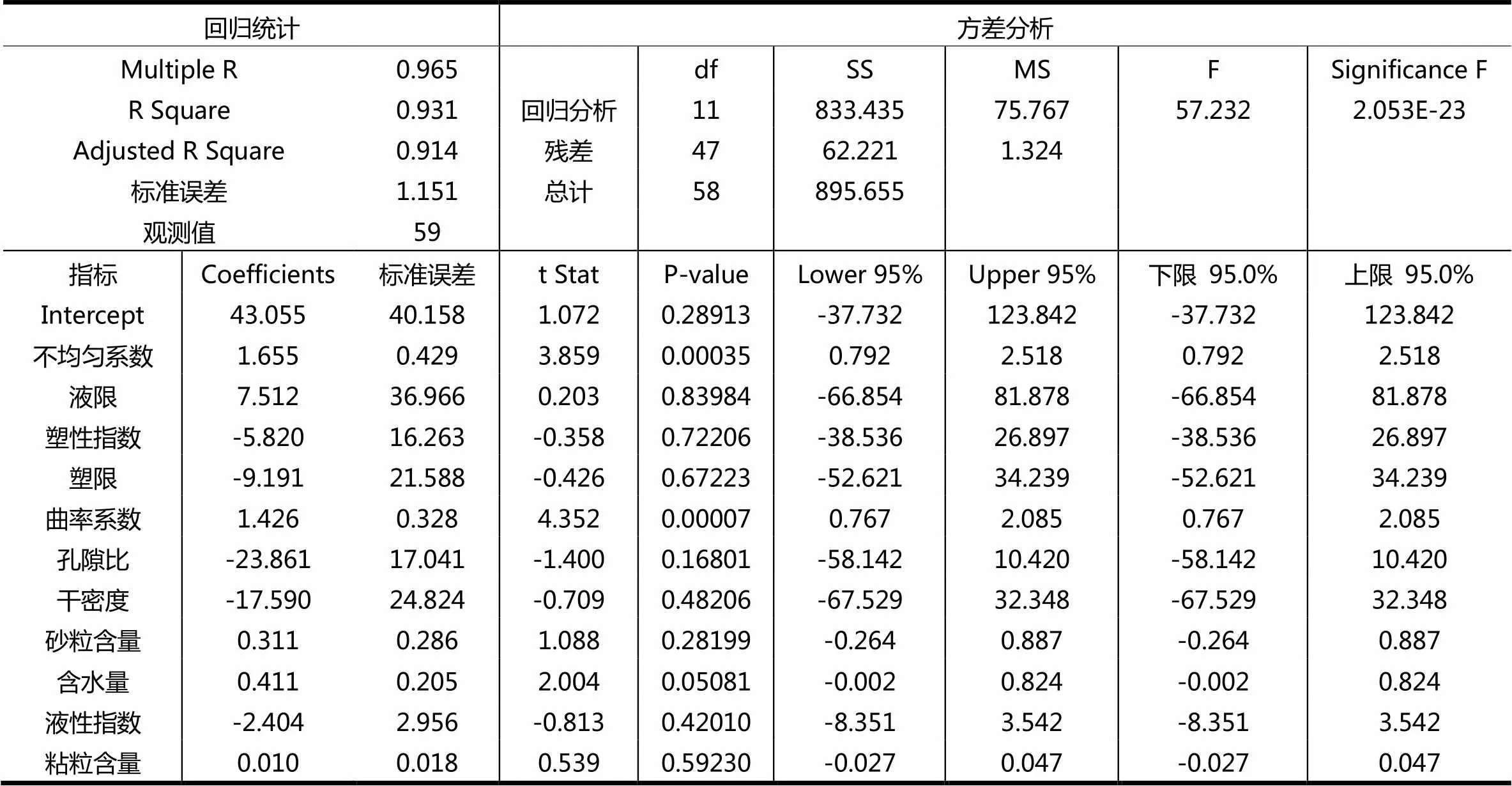
表3 内摩擦角多元线性回归分析结果

3 粘性土基本物理指标与内摩擦角的多因素相关性

根据物理指标与内摩擦角的单因素分析结果，假定内摩擦角与物理指标间服从多元线性关系，即：

￠=b0+b1×ln（Cu）+ b2×ln（Wl）+ b3×ln（Ip）+ b4×ln（Wp）+ b5×

ln（Cc）+b6×ln（e）+ b7×rd+ b8×ln（S）+ b9×w+ b10×Il+ b11×N （1）

利用EXCEL对式（1）进行多元线性回归分析，回归分析结果列于表3。

由表4的多元回归分析结果看以看出，回归方程复相关系数R2=0.965，其F值57.232远大于显著性F值2.053E-23（α=0.05），说明回归方程精度较高，但部分指标的P值超过了0.05（α=0.05），一方面是部分指标与内摩擦角的相关性本身就不高，另一方面，指标之间存在共线性的问题，如孔隙比与干密度，液限、塑限与塑性指数，液性指数与含水量、塑性指数等，为消除指标之间的共线性和相关性不大的指标，将回归分析结果中超过0.05的最大P值对应的指标剔除，取余下的指标进行多元回归分析，直至所有指标的P值均满足要求后停止。最终得到不均匀系数、塑性指数、曲率系数、孔隙比和含水量等五个物理指标与内摩擦角的回归分析结果列于表4。

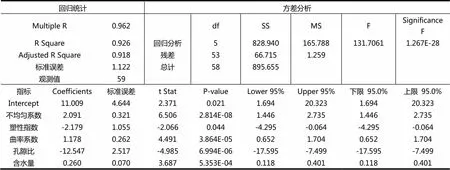
表4 内摩擦角多元线性回归分析结果

由表5的结果知，粘性土内摩擦角与粘性土不均匀系数、塑性指数、曲率系数、孔隙比和含水量之间的复相关系数为0.962，调整复相关系数的平方为0.918，说明影响粘性土内摩擦角91.8%的因素可由粘性土的不均匀系数、塑性指数、曲率系数、孔隙比、含水量等来解释。

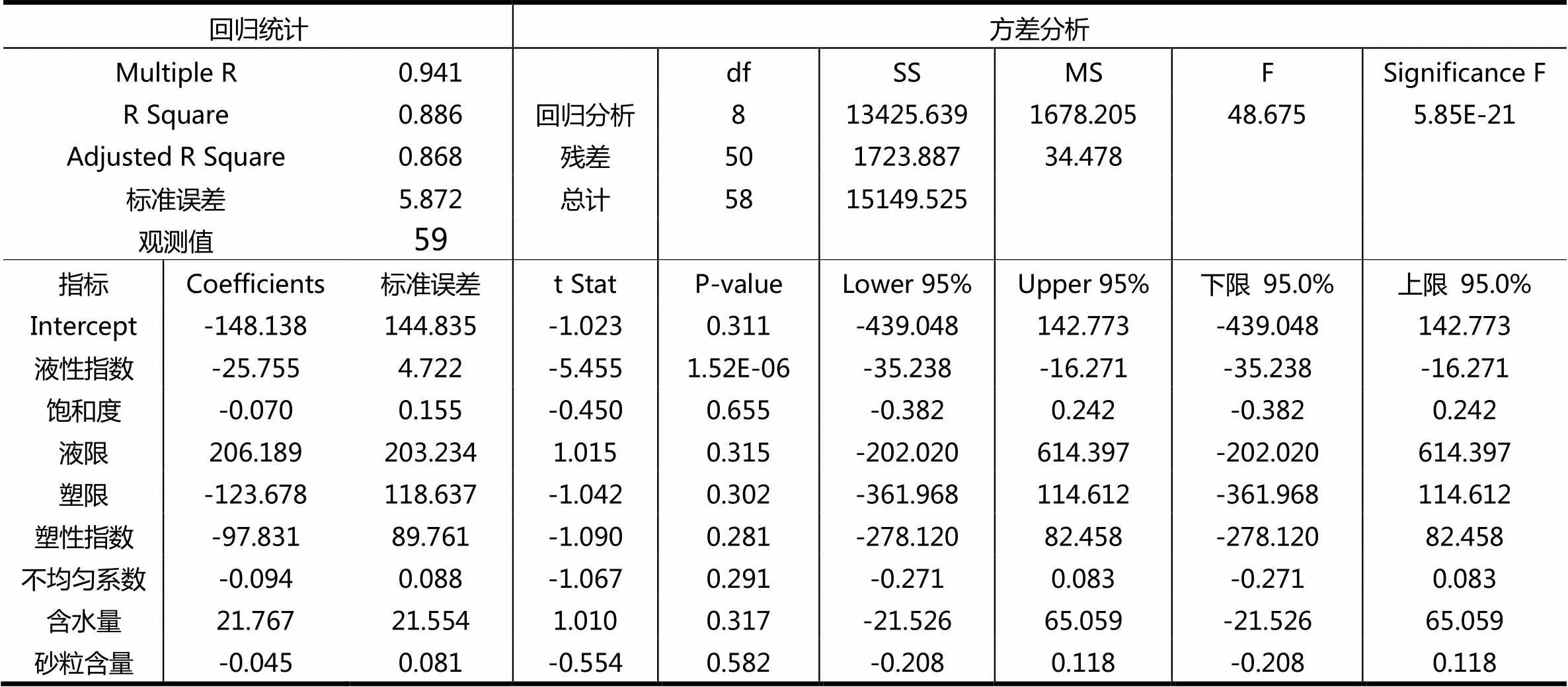
表5 凝聚力多元线性回归分析结果

不均匀系数、曲率系数反映了粘性土中颗粒的分布情况，塑性指数反映了土的分类，孔隙比反映了粘性土的密实程度，含水量反映了粘性土的饱和程度。数据分析结果与一般认识是吻合的。

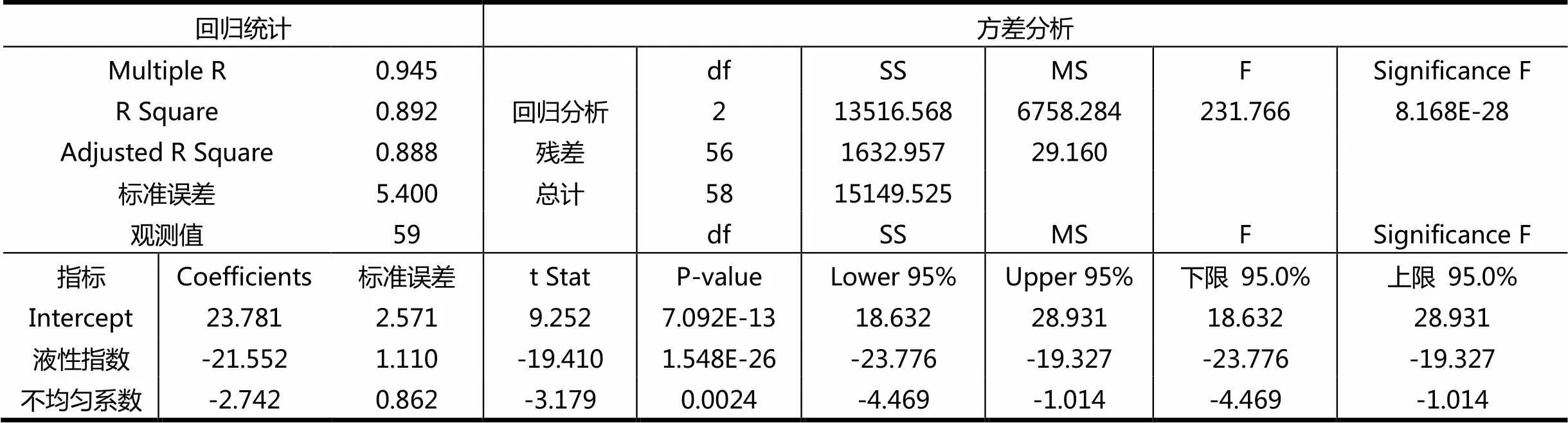
表6 凝聚力多元线性回归分析结果

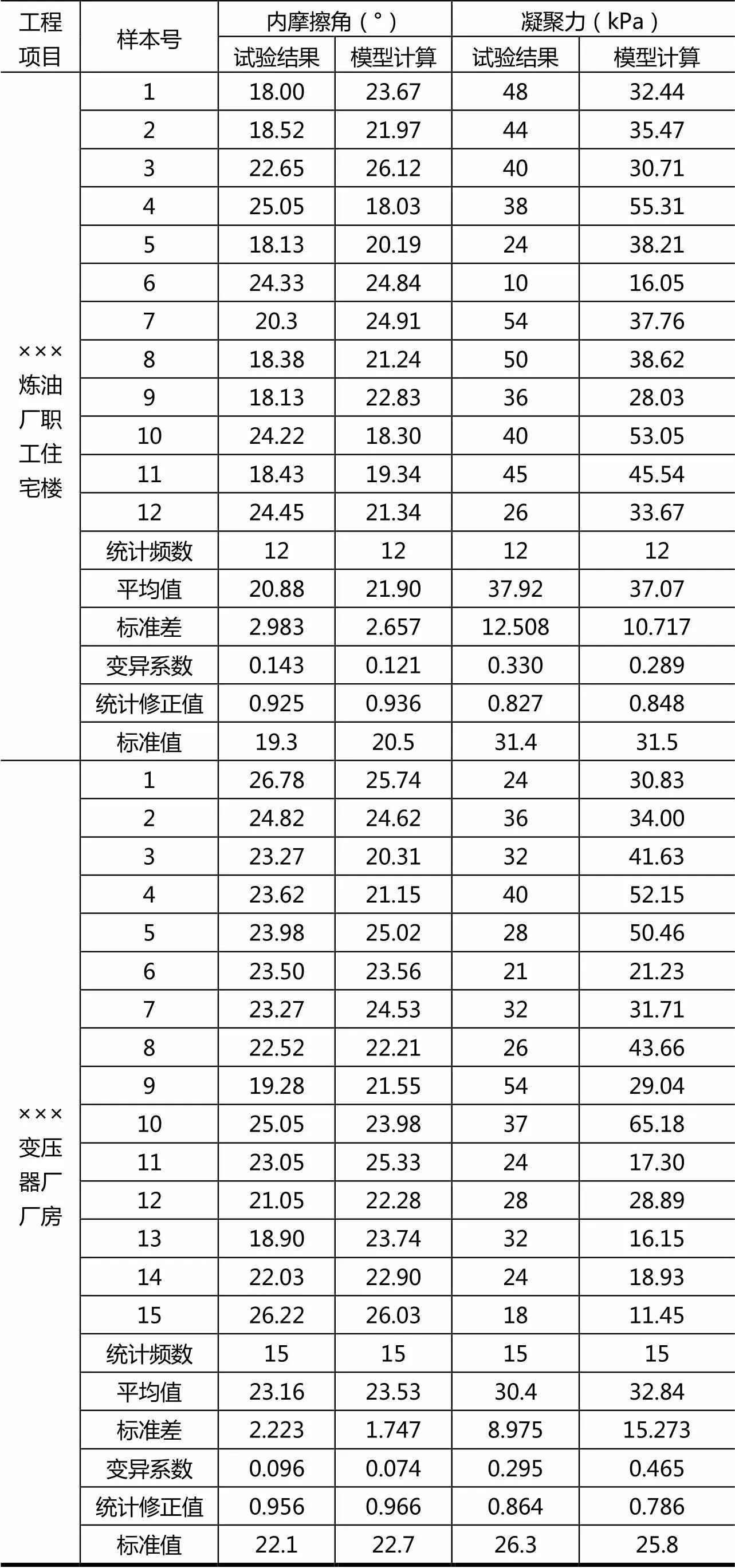
表7 ××炼油厂职工住宅楼场地土样抗剪强度参数标准值比较

4 粘性土基本物理指标与凝聚力的多因素相关性

根据物理指标与内摩擦角的单因素分析结果，同样假定凝聚力与物理指标间服从多元线性关系，即：

C=b0+b1×ln（IL）+ b2×Sr+ b3×ln（WL）+ b4×ln（WP）+ b5×ln（IP）+ b6×Cu+ b7×ln（w）+ b8×S （2）

利用EXCEL对式（3）进行多元线性回归分析，回归分析结果列于表5。

由表6的多元回归分析结果看以看出，回归方程复相关系数R2=0.941，其F值48.675远大于显著性F值5.85E-21（α=0.05），说明回归方程精度较高。与内摩擦角初次分析结果相似，部分指标的P值超过了0.05（α=0.05），一方面是部分指标与凝聚力的相关性本身就不高，另一方面，指标之间存在共线性的问题，如液性指数、饱和度与液限、塑限、含水量和塑性指数等，为消除指标之间的共线性和相关性不

大的指标，将回归分析结果中超过0.05的最大P值对应的指标剔除，取余下的指标进行多元回归分析，直至所有指标的P值均满足要求后停止。最终得到液性指数、不均匀系数等二个物理指标与凝聚力的回归分析结果列于表6。

由表6的结果知，粘性土凝聚力与粘性土液性指数、不均匀系数之间的的复相关系数为0.945，调整复相关系数的平方为0.888，说明影响粘性土凝聚力88.8%的因素可由粘性土的液性指数和不均匀系数来解释。

液性指数反映了粘性土的软硬程度，不均匀系数反映了粘性土中颗粒大小的分布情况。数据分析结果与一般认识也是是吻合的。

5 粘性土抗剪强度参数的统计模型

基于上述59个样本的统计分析，估算粘性土抗剪强度参数的统计模型为：

￠=11.009+2.091lnCu-2.179lnIp+1.178lnCc- 12.547lne+ 0.260w （3）

C=23.781-21.552lnIL-2.742lnCu （4）

6 工程实例

×××炼油厂职工住宅楼场地地基共取土样12组[6]、，×××变压器厂厂房场地地基共取土样15组[7]，基于统计模型预测的抗剪强度参数标准值与按试验成果计算的抗剪强度参数标准值列于表7。

表7表明，模型计算的粘性土抗剪强度参数标准值与试验结果统计的标准值非常接近，该模型十分具有使用价值。

7 结 语

粘性土的内摩擦角与粘性土的不均匀系数、曲率系数、塑性指数、孔隙比和含水量等物理指标密切相关，对内摩擦角影响程度最大的是粘性土的不均匀系数。

粘性土的凝聚力与粘性土的液性指数和不均匀系数等物理指标关系密切，对凝聚力影响程度最大的

是粘性土的液性指数。

本文建立的统计模型精度较高，可用于本地区工程实践。

为满足需要，其他地区可探索建立适用于本地区的相关模型。

[1]中华人民共和国建设部. GB50021-2001 岩土工程勘察规范（2009年版）[S].北京：中国建筑工业出版社，2009.

[2]杨英华. 土力学[M]. 北京：地质出版社，1987.

[3]卢肇均. 杨伟. 软土内摩擦角和塑性指数的关系[C]. 第一届全国土力学及基础工程学术会议论文选集. 北京：中国建筑工业出版社，1962.

[4]卢肇均. 曾昭群. 对粘性土内摩擦角的探讨[C]. 第六届全国土力学及基础工程学术会议论文选集. 上海同济大学出版社，中国建筑工业出版社，1991.

[5] 四川南充水利电力建筑勘察设计院. 1986年土工试验报告汇总[R]. 1986

[6] 四川南充水利电力建筑勘察设计院. 1988年土工试验报告汇总[R]. 1988.

[7] 郑德如. 回归分析和相关分析[M]. 上海：上海人民出版社，1984.

A Statistical Model for Estimating Shear Strength Parameters of Cohesive Soil

LI Yun

（Nanchong Research Institute of Investigation and Design of Water Conservancy, Hydropower & Architecture, Nanchong, Sichuan 637000）

The mechanical properties of soil body are closely related to its basic physical properties. Test procedure of the mechanical index is usually overelaborate and time-consuming, while the physical index test is relatively simple and fast. It is one of the basic tasks of soil mechanics to establish the quantitative relation between physical index and mechanical index of soil body. Based on the single factor regression analysis of the basic physical indexes and shear strength parameters of cohesive soil, and taking the correlation coefficient r≥0.4 as the primary index, the multivariate regression analysis is carried out, at all a statistical model for estimating the shear strength parameters of the cohesive soil is established. The test of the model shows that the statistical model has practical application prospect.

cohesive soil; physical index; shear strength parameter; statistical model

2018-03-05

李云（1970—），男，四川西充人，高级工程师，主要从事岩土工程设计、试验研究及水利工程质量检测工作

P642.1

A

1006-0995（2018）04-638-06

10.3969/j.issn.1006-0995.2018.04.023