基于MSC-Adams的桥式卸船机抓斗摆动自动控制研究

虞上长,杨明花,杨勇,李楠

基于MSC-Adams的桥式卸船机抓斗摆动自动控制研究

虞上长1,杨明花1,杨勇1,李楠2*

1. 浙江浙能温州发电有限公司, 浙江 温州 325602 2. 杭州集益科技有限公司, 浙江 杭州 311215

针对传统桥式卸船机抓斗摆动防撞控制的不足之处，本文构建了一个抓斗小车虚拟动力学系统，并基于MSC-Adams构建了多股钢丝绳的离散刚体，Bushing策略构建出钢丝绳链接模型。针对无摇摆防撞控制下的桥式卸船机抓斗进行仿真，具体探讨了空气阻力和抓卸料等因素对于桥式卸船机抓斗摇摆防撞的影响，仿真结果表明多种因素影响到抓斗摇摆防撞控制。最终，分析抓斗摆动教育和小车对抓斗相对速度的关系，得出桥式卸船机抓斗摆动曲线，制定出抓斗摇摆防撞控制策略。

桥式卸船机; 抓斗; 摆动控制

桥式卸船机在完成卸料任务的过程中，通常需要进行小车加速、抓斗上升引发的风力带来的空气阻力，从而导致卸船机的卸料抓斗出现摇摆的现象[1]。当抓斗出现严重摇摆的时候，有较大的风险出现撞击等危险，并且也会严重影响卸船机卸料的作业效率。在高空作业过程中，卸船机的结构增加了载荷，容易引起结构失效，造成较大的安全隐患[2]。因此，在桥式卸船机的卸料任务中，构建抓斗的摇摆防撞控制策略，能够提升卸船机的自动化和效率[3]。在构建桥式卸船机抓斗和小车系统的动力学模型的研究中，国内外的主流观点均采用解析模型构建出动力学模型[4-6]。解析模型的缺陷是在动力学模型中无法考虑率钢丝绳的力学特性和装配结构带来的影响因素，无法考虑实际作业中由于起升联动效应导致对钢丝绳的变化，此外风力干扰的不确定性也不能被考虑在内[7,8]。因此，传统的解析模型不能够全面解析卸船机抓斗和小车系统中的动力学特性。

在本文中，通过使用MSC-Adams机械动力学建模软件，构建卸船机抓斗和小车系统的数学仿真模型，该模型可以通过离散刚体柔性连接方法完成对钢丝绳的建模，以及其他数学模型完成对空气阻力和抓卸料的有效建模。通过该数学仿真模型，即可对卸船机抓斗的摇摆特性完成仿真，通过仿真结果可以对抓斗防撞控制策略进行分析和设计。

1 桥式卸船机抓斗和小车虚拟动力学系统

为了构建桥式卸船机抓斗和小车的虚拟动力学系统，文中以散货码头上的2100 t/h的桥式卸船机作为原型[9]，构建出虚拟动力学系统。

1.1 抓斗小车动力学模型

在系统动力学仿真模型中，小车部件是整个桥式抓斗机的驱动部分，因此小车中包含了滑块、滚筒和辅助滚轮三个组成部分。下图1(a)给出了小车部件的MSC-Adams仿真模型。

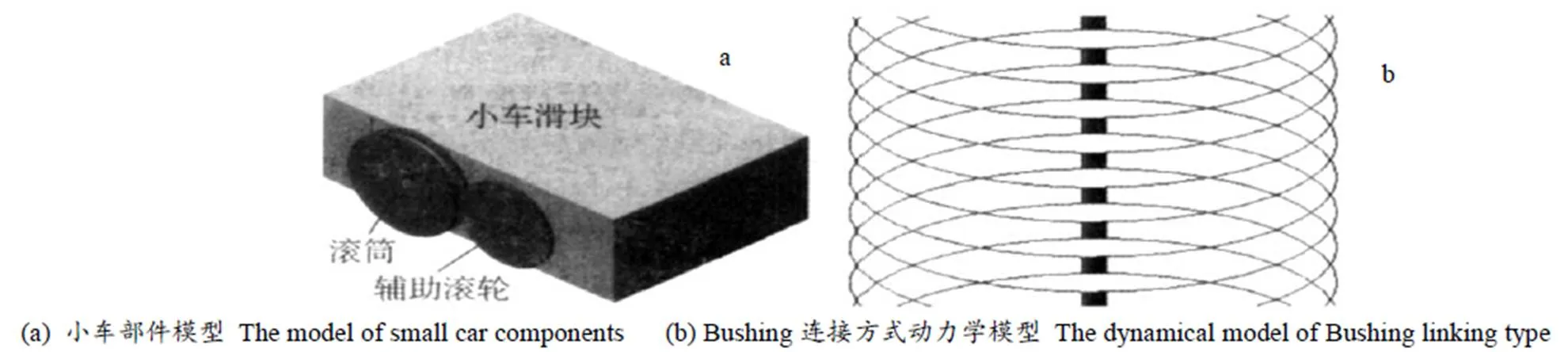
图 1 动力学系统的MSC-Adams仿真模型

在小车部件的仿真模型中，滑块是驱动小车进行水平运动的驱动力，而滚筒则与简化后的钢丝绳相连，小车驱动滚筒运动将会导致钢丝绳的驱动，该驱动力则可以用于抓斗的升降运动。辅助滚轮在侧边与钢丝绳相连，保障钢丝绳在被滚筒驱动过程中的鲁棒性，三个模块之间采用转动铰约束实现连接[10]。

1.2 多股钢丝绳弹性模型

钢丝绳在动力学系统中的主要作用是实现小车和抓斗之间的柔性连接，通过与小车的滚筒连接，让小车的水平运动引发钢丝绳的卷绕运动，卷绕运动驱动抓斗的升降，完成抓斗的卸料作业[11]。图1(b)给出了基于离散圆柱微段及采用Bushing连接方式的动力学模型。

一般来说，抓斗到达最大高度时钢丝绳的长度嘴短，此时的动力学模型应该保证离散个数足够大，才能够保证抓斗摇摆仿真的准确度。实际上，根据离散个数，可以通过下式确定钢丝绳的离散总数：=×((+)/) (1)

根据平衡计算量和仿真精度，文中可以选择微段长度220 mm，设置=152。如果不进行模型的简化，相应钢丝绳的离散总数可以形成103的量级，通过相关约束将会产生更大的运算量，所以在本文中对动力学模型进行简化，并且不再考虑相关约束，从而减少运算量。

在MSC-Adams的仿真建模中，文中采用Bushing方式在两个部件之间形成相互的作用力。在实际的动力改写模型中，文中定义六个力矩分量{F,F,F,T,T,T}，通过这些力矩分量来形成两个构建之间的柔性连接。下图2给出了Bushing方式形成部件之间的柔性连接示意图。

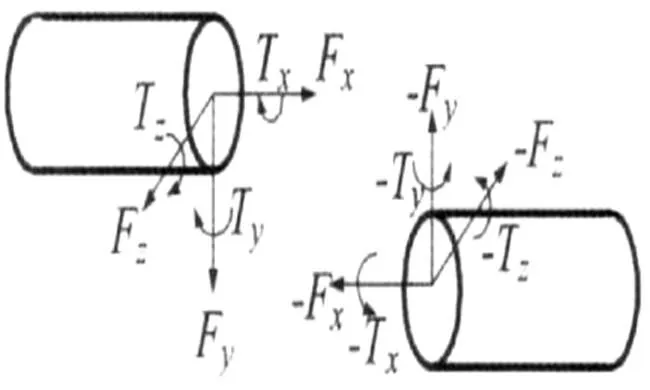
图 2 Bushing方式形成部件之间的柔性连接示意图

在上图的Bushing模型中，六个刚度系数和六个阻尼系数将会影响到钢丝绳模型的精确程度，因此需要通过精准计算来确定。本文通过文献[9]中给出的方法来确定钢丝绳模型中的刚度系数和阻尼系数。实际的数值确定为，将四根钢丝绳进行等效分析，六个阻尼系数均设置为20，然后在此基础上通过对钢丝绳的装配和本体结构计算力学性能，计算出修正系数对模型进行弹性和剪切模量进行修正。在六个阻尼系数的基础上，通过下式计算出六个刚性系数：

其中，11表示为拉伸系数；22，33表示为剪切系数；44表示为扭转系数；55，66表示为弯曲系数；1，2，3，4分别为结构修正系数；和分别为弹性和剪切模量，，，分别表示钢丝绳的截面积、微段长度和惯性矩。

1.3 抓斗中的抓卸料与空气阻力模型

其中，F表示的是空气阻力；表示的是空气阻力系数，取固定值为0.4。表示的是抓斗迎风的面积，取固定值为12 m2；表示的是空气密度，取固定值为1.2258 Ns2/m4；表示的是抓斗的运动速度。

2 动力系统仿真与抓斗摇摆防撞控制分析

2.1 仿真实验与结果

为了验证本文构建的动力学系统仿真模型的可行性和有效性，分别针对该动力学系统进行无摇摆控制和有摇摆防撞控制分析。下图3给出了模型针对无摇摆控制、起升联动工况仿真后的运动轨迹。针对实际的公开，在滚筒和小车之间通过转动铰约束来构建系统的转动运动，并在小车和大车之间的水平方向上施加水平移动运动，下图4(a)给出了滚筒和小车之间转动铰约束形成的模型驱动速度曲线。

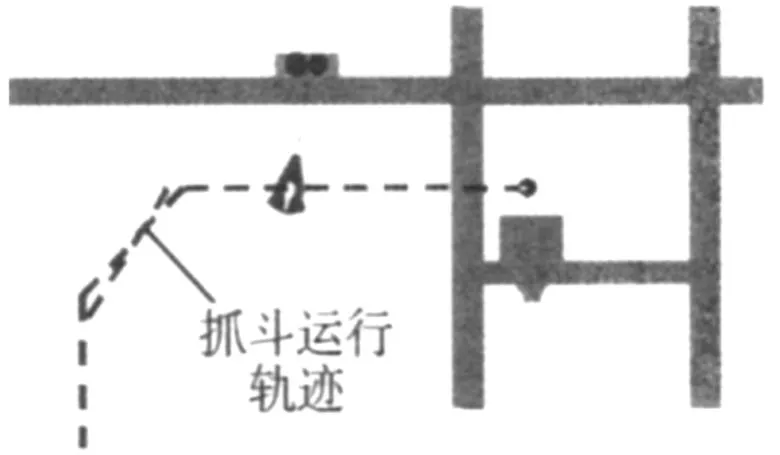
图 3 无摇摆控制、起升联动工况仿真模型的运动轨迹

图 4 仿真实验结果曲线

针对仿真结果进行进一步的分析，图4(b)给出了抓斗摇摆角度与时间的关系图。从上图的结果中可以看出，针对桥式卸船机抓斗的抓卸料和空气阻尼对抓斗摆角幅值之间存在如下的关系：当卸船机抓斗卸料完成后，质量发生减小，导致抓斗的摆动幅度增大，仅仅只通过钢丝绳和空气的力产生的阻尼并不足以快速减小抓斗摆角幅值，也就是仅仅依靠钢丝绳并不能直接完成对抓斗防撞的控制策略。因此，上述的结果表明了本文构建的动力学仿真模型符合实际的情况，有较高的正确性，针对抓斗摆动的防撞策略和控制是有必要的。

2.2 抓斗摇摆防撞控制分析

实际上，要研究桥式卸船机抓斗摇摆的防撞控制策略，必须研究小车、抓斗之间的关系。也就是说，需要满足小车匀速运动时，需要保证抓斗无摆动。上述的条件可以转化为，当轿车达到最大速度的时候，抓斗卸料后摆动的最大角度与小车对抓斗相对速度同时为0，所以需要分析抓斗摆动与小车对抓斗相对速度之间的关系。根据图5中给出的速度关系可以看出：

（1）小车与抓斗之间相对速度为0的时刻是抓斗呈现出极值摆角的时刻；

（2）当抓斗的摆角为0的相应时刻，是小车对抓斗之间的相对速度到达极值的时刻。

因此，针对抓斗卸料后的摇摆防撞策略分析，需要保证小车达到最终速度时，抓斗此时的摆角为0并且此时恰好为极值点，也就是在该时刻，摆角的曲线和时间轴呈现相切的关系。

桥式卸船机的抓斗摆动不利于卸船机结构的实际寿命，并且容易造成生产作业出现安全隐患的问题，因此桥式卸船机的抓斗摆动防撞策略能够最大程度较少整个卸料过程中抓斗摆角的幅值总量。因为抓斗的摆动程度是实现抓斗在卸料过程中加速度的必要条件，因此需要抓斗摆角的幅度总值量呈现最小，也就是在小车进行启动和制动过程中，抓斗的摆角不能穿越零点。针对上述分析，文中通过下图5给出了理想状态下桥式卸船机抓斗摆动防撞策略。在图中，中间的点线表示的部分为抓斗摆角不确定的时间段。

图 5 理想状态下桥式卸船机抓斗摆动防撞策略

3 结语

在本文中，基于MSC-Adams软件构建了一个桥式卸船机的抓斗和小车动力学系统仿真模型，通过仿真实验验证本文提出模型的可行性和有效性，仿真结果对于抓斗摇摆防撞控制的分析表明，理想状态下的抓斗摇摆曲线是一条位于小车开始和结束加速时间段内与两端时间相切，除两段外再无与其他时间节点有交点的曲线。今后的工作集中在考虑更多的环境影响因素来构建更理想的桥式卸船机抓斗系统动力学模型，通过更有意义的系统动力学模型，构建出更加鲁棒、更高性能的抓斗摆动防撞策略。

[1] 方关有,李铁.桥式抓斗卸船机机房底架加强筋布局优化分析[J].起重运输机械,2018(7):150-152

[2] 袁彦青,雷步忠,高翔.桥式抓斗卸船机在内河流域的滚装运输方案[J].起重运输机械,2017(10):159-161

[3] 张逸国,李林.交流变频技术在桥式自行小车式卸船机改造中的应用[J].起重运输机械,2007(8):70-74

[4] 叶永伟,陆俊杰.基于ANSYS的桥式抓斗卸船机结构抗震性能分析[J].机电工程,2017,34(9):986-992

[5] 殷江平.桥式卸船机检测应力的正确理解和应用[J].起重运输机械,2015(2):97-99,100

[6] 刘耀杰.桥式抓斗卸船机差动减速器工作原理[J].起重运输机械,2017(9):69-71

[7] 刘秀华,谢剑刚.桥式抓斗卸船机滑轮座底部裂纹的处理及分析[J].起重运输机械,2011(5):88-90

[8] 李宪晔,程从山,杨文武,等.650 t/h桥式卸船机卷筒装置故障分析及其改进措施[J].新技术新工艺,2010(11):28-29

[9] 何成忠,刘汉东.桥式抓斗卸船机应力测试技术应用[J].起重运输机械,2012(8):100-103

[10] 马文舒,林金栋,张建国.桥式抓斗卸船机的发展与现状分析[J].起重运输机械,2014(11):1-4

[11] 呙中樑,谢超,王新华,等.桥式抓斗卸船机的振动模态分析[J].重型机械,2014(5):47-50

[12] 赵红朋.桥式抓斗卸船机钢丝绳旋转机理及预防措施[J].港工技术,2011,48(3):16-19

Research on Autocontrol for the Grab Bucket Swing of Bridge Type Ship Unloader Based on MSC-Adams

YU Shang-chang1, YANG Ming-hua1, YANG Yong1, LI Nan2*

1.325600,2.311215,

Aims to the shortages of conventional ridge type un-loader grab swing self-controlling and anti-collision strategies, this paper constructed a novel grab-car virtual dynamic system. After construction of dynamic systems, we constructed discrete rigid bodies for multiple steel wire ropes based on MSC-Adams technology. Then, the Bushing strategy was constructed based on the steel wire rope models, and such strategy was useful for improving the elastic modules of steel wire ropes. Simulation experimental results showed that there existed multiple factors that influenced the anti-collision strategy of grab swing. Based on the multiple influenced factors, we analyzed the relationships between the magnitude of grab swing and the speed of small car. Analysis results demonstrated the swing curves of bridge type unloader grab, and we also designed the anti-collision strategy for the grab.

Bridge typr unloader; grab bucket; swing control

O231

A

1000-2324(2018)06-1040-04

10.3969/j.issn.1000-2324.2018.06.027

2018-01-23

2018-03-11

虞上长(1966-),男,硕士,高级工程师,研究方向:火力发电厂设备自动控制及Adams动力学分析. E-mail:2810621483@qq.com

Author for correspondence. E-mail:eslinan@gmail.com