一维泊松方程的结构优化及对PDEs的精确解

张秀英



一维泊松方程的结构优化及对PDEs的精确解

张秀英

郑州铁路职业技术学院, 河南 郑州 451460

关于PDEs的精确解问题，在实际求解中较为困难。本文以一维泊松方程为例，结合Lie对称方法和Wu方法分析方程的古典对称，计算单参数的无穷小向量，并设计方程的最优结构，通过两个定义得出一维泊松方程的最优换位和伴随算子，由此优化方程结构。以此为基础计算一维泊松方程最优结构单个元素对PDEs的精确解，在两种古典对称情况下，分别求出对PDEs的两个新解。此结果对PDEs精确解问题是一次有新意的尝试。

一维泊松方程; PDEs; 精确解

泊松方程属于一种偏微分方程（PDEs），在静电学和机械工程学中经常用到。关于PDEs的求解较为困难，常用的是Lie对称方法，通过Lie解析PDEs的对称性，由此找到精确解。但是对称群的子群通常无穷多，这赋予了精确解无穷多的可能性。为了找出等价的精确解，需要分类所有子群[1]。对于一维泊松方程来说，它的结构优化至关重要，最优结构下的一维泊松方程可以有效拓展应用领域，并且成为PDEs求解的关键之一。Lie对称方法尽管能够确定泊松方程的无穷小向量，但数据量大，计算过程复杂。而Wu方法能够克服这一缺陷。最近几年以来，Wu方法在微分领域得到了一定推广，该方法最早应用于纯代数领域，但它的一些算法适用于PDEs对称和分类问题的解决，展现出较高的应用价值。通过一维泊松方程的结构优化以及对PDEs的精确解，拓展了PDEs的求解途径。

1 一维泊松方程的结构优化

1.1 一维泊松方程对称性分析

一维泊松方程如式（1）所示：u+2uu-(1-)u=0 (1)

上式中(,,)、(,,)、(,,)作为对称向量无穷小的函数。按照Lie算法可以得出与方程（1）所对称的确定方程组，但难以手动进行求解。以Wu的微分特征算法可以计算出与该确定方程组相对应的特征方程组：===0，==0，==0，-=0，-=0

对以上方程组进行求解，得出无穷小函数：=1+2，=1+5，=1+3+4

在以上函数中，1到5属于任意函数，无穷小的向量则能用以下公式计算：

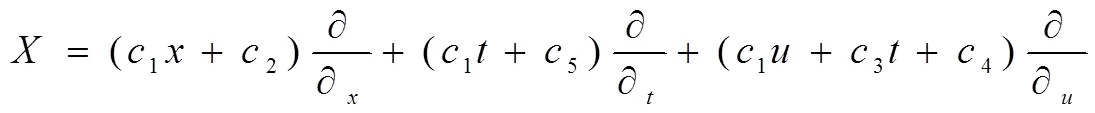
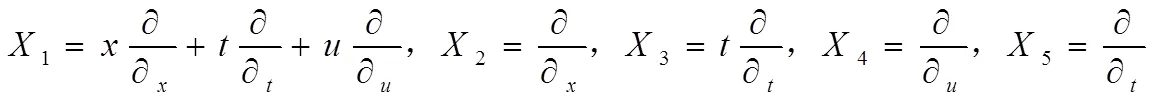
1.2 一维泊松方程的最优结构

计算出公式（1）各对称参数的无穷小向量，就可以分析一维泊松方程的最优结构。

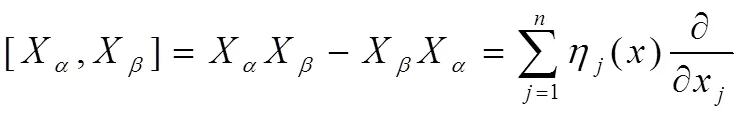
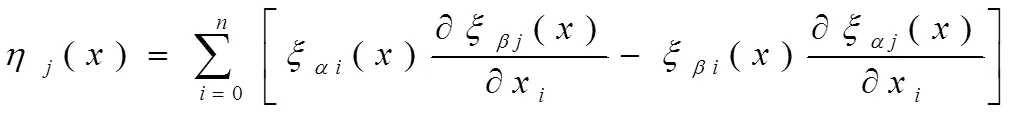
由此得出下面等式：[X,X]=-[XX]

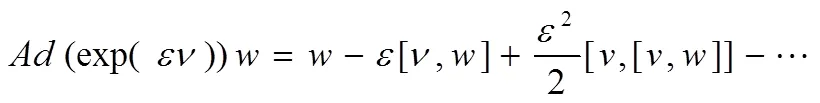
按照以上两个定义，得出公式（1）的最优换位和伴随算子，如表1和表2所示。

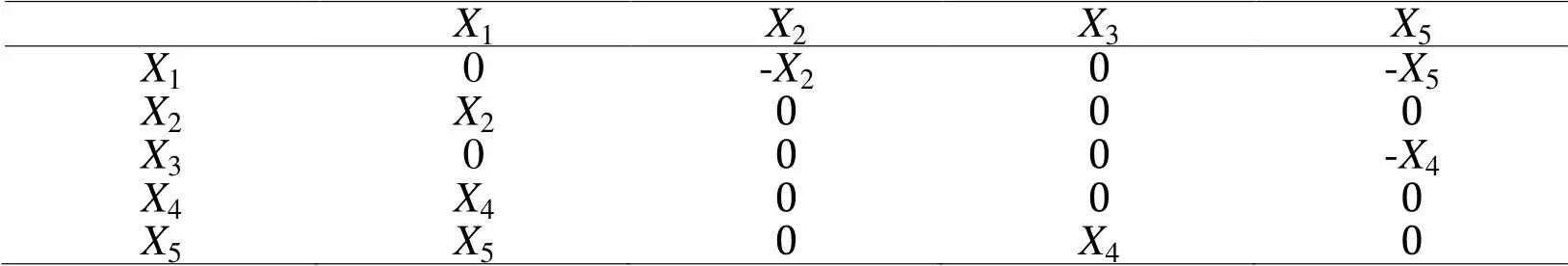
表 1 一维泊松方程最优换位表

表 2 一维泊松方程的伴随算子表

按照一维泊松方程最优结构的求解方法，假设Î5¹0，由5构建Lie代数，公式如下：

=11+22+33+44+55(2)

上式中的1到5属于任意常数。

（1）设1¹0，若使1=1，公式（2）可用以下表示：=1+22+33+44+55

设¢=(exp(3))，计算之后以下等式成立：¢=1+(2-)2+33+(4+5)4+55

使=2，以下等式成立：¢=1+33+(4+25)4+55

在¢中作用(exp(5))，则²=(exp(5))¢，在计算之后以下等式成立：

²=1+33+(4+25-3)4+(5-)5

设=5，则²=1+33+(4+25-35)4。在²中作用(exp(4))，则²¢=(exp(4))²，在计算之后以下等式成立：²¢=1+33+(4+25-35-)4

设=4+25-35，则²¢=1+33。由此可知伴随算子到这一步将无法继续使用。

（2）设1=0，5¹0，若使5=1，公式（2）可用以下表示：=22+33+44+5

在¢中作用(exp(3))，则¢=(exp(3))，计算之后等式¢=22+33+(4-)4+55成立。

设=4，则¢=22+33+55。由此可知伴随算子到这一步将无法继续使用。

（3）设1=5=0，2¹0，若使2=1，公式（2）可用以下表示：=2+33+44

在中作用(exp(5))，则¢=(exp(5))，计算之后以下等式成立：¢=2+33+(4-3)4

设=4/3，则¢=2+33。由此可知伴随算子到这一步将无法继续使用。

（4）设1=2=5=0，3¹0，若使3=1，公式（2）可用以下表示：=3+44

在中作用(exp(5))，则¢=(exp(5))，计算之后以下等式成立：¢=3+(4-)4

设=4，则¢=3。由此可知伴随算子到这一步将无法继续使用。

（5）设1=2=3=5=0，4¹0，若使4=1，则=4。由此可知伴随算子至此将无法继续使用。

根据以上5个步骤的分析，一维泊松方程的最优结构如下：

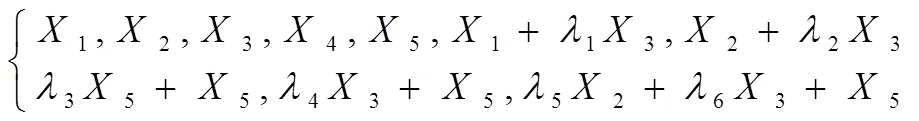
2 一维泊松方程对PDEs的精确解

根据式（4）可得出不变量=/，由于()/=()/(+)，得出=-+()，代入式（1）可得：

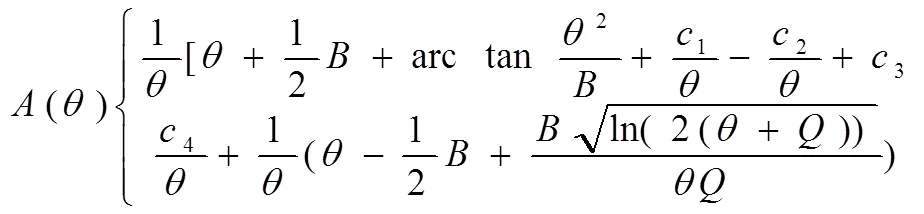
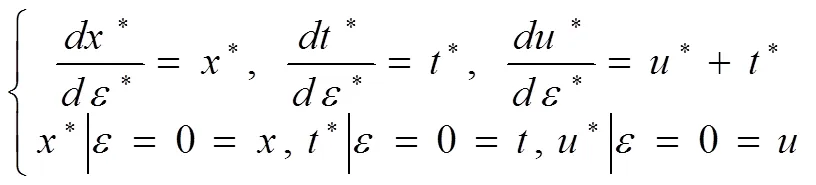
将以上变换群在精确解1(,)中进行作用，得出对PDEs的另一个新解：

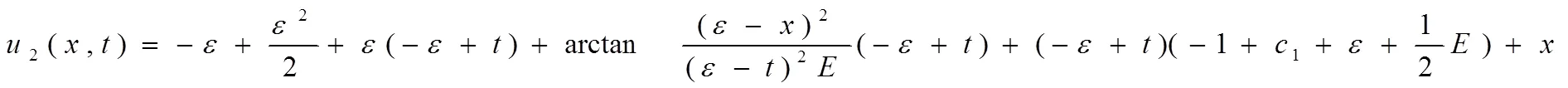
3 讨论

关于PDEs的求解问题，国内外学者进行了深入的探索。法国学者Mazurenko为了控制PDEs的模糊边界，提出了一种边界控制模型，该模型需要PDEs的精确解支撑，他提出了PDEs精确求解的几种方法[2]。Arshed综合了国际数学界关于PDEs求解的相关经验做法，提出一种随机偏微分方程最优控制方法，其中就涉及到PDEs精确解问题[3]。朝鲁教授在研究微分算法应用中，提出了Wu算法在PDEs求解中的使用，以此得出平面应力方程组的古典对称[4]。李吉娜等通过广义条件对称法，对偏微分方程的对称约化问题进行研究，使偏微分方程的初值约化得到解决[5]。总体来看，PDEs求解问题的彻底解决，还有很长一段路要走，但随着国内外相关学者的努力，会有越来越多的方法。

4 结论

PDEs求解在工程领域的应用越来越普遍，尤其计算它的精确解更为重要。泊松方程作为PDEs的一个分支，通过一维泊松方程求对PDEs的精确解有一定代表性。本文结合Lie对称方法和Wu方法分析一维泊松方程的古典对称，设计出该方程的最优结构，并计算最优结构中相应元素的Lie变换群，分析最优结构单个元素对PDEs的精确解，在两种古典对称情况下，得出对PDEs的两个新解。此结果对PDEs精确解问题的解决开拓了一条新途径。

[1] Yebdri M. On Weak Solutions of a Functional Differential Equation[J]. International Journal of Applied Mathematics & Statistics, 2018,57(2):125-127

[2] Stanislav M. Partial Differential Equation for Evolution of Star-Shaped Reachability Domains of Differential Inclusions[J]. Set-valued and variational analysis, 2016,24(2):333-354

[3] Saima A. B-spline solution of fractional integro partial differential equation with a weakly singular kernel[J]. Numerical Methods for Partial Differential Equations: An International Journal, 2017,33(5):1565-1581

[4] 朝鲁.产生和求解PDEs对称确定方程组的微分特征列集算法理论及其应用[J].内蒙古大学学报:自然科学版,1988(3):16-21

[5] 李吉娜,杨静,陈媛媛,等.一类三阶偏微分方程的对称约化[J].数学的实践与认识,2018(14):287-292

Structural Optimization of One-dimensional Poisson Equation and Its Exact Solution to PDEs

ZHANG Xiu-ying

451460,

The exact solution of PDEs is difficult in practice. Taking one-dimensional Poisson equation as an example, the symmetry of the equation is analyzed by Wu method, and the optimal structure of the equation is designed. The optimal transposition and adjoint operators of one-dimensional Poisson equation are obtained by two definitions, thus the structure of the equation is optimized step by step. On this basis, the exact solution of PDEs for single element of optimal structure of one-dimensional Poisson equation is calculated by invariant method. Under two classical symmetry conditions, two new solutions for PDEs are obtained respectively. This result is a new attempt to solve PDEs precisely.

One-dimensional Poisson equation; PDEs; exact solution

O29

A

1000-2324(2018)06-0995-03

10.3969/j.issn.1000-2324.2018.06.018

2018-03-12

2018-05-10

2017年度河南省高等教育教学改革研究与实践项目(2017SJGLX570);2018年度河南省高等学校重点科研项目计划(19B880029)

张秀英(1965-),女,本科,副教授,主要研究方向为数学教育、数学建模教学研究. E-mail:zhangxiuying588@163.com