基于J-C模型的TC18钛合金动态本构方程构建

贾宝华，刘思勇，李 革，刘 翔，王丹丹

(内蒙古科技大学，内蒙古 包头 014010)

0 引 言

TC18钛合金(苏联牌号为BT22)是在20世纪70年代，由苏联研制出的一种α+β型高强钛合金，名义成分为Ti-5Al-5Mo-5V-1Fe-1Cr[1-2]。它具有高韧性，高强度，优良的塑性、淬透性、锻透性和良好的焊接性等特点[3-5]。TC18钛合金在退火状态下，强度可达1 080 MPa，经过强化处理后，最高强度可以达到1 300 MPa，淬透深度可达250 mm[6-7]。由于TC18钛合金在截面厚度方向上基本没有淬透性的限制，所以可以采用热模锻、等温模锻和普通低成本模锻等热加工工艺来进行锻件的生产，因此适合制造飞机上各种高承载力构件，包括起落架、支架、横梁以及一些紧固件和弹簧等[8-11]。

对于在航空领域中被广泛用于制作各种高承力构件的TC18钛合金，其工作时不可避免的要承受冲击载荷作用，因此对其动态力学性能方面的研究十分必要。但由于TC18钛合金在准静态下的强度非常高，再加上材料的应变率效应，如果要进行动态冲击实验，必须选择有足够强度的霍普金森杆件，既要保证被测试的TC18钛合金发生塑性变形，又要保证霍普金森杆件自身处于弹性状态，因此国内外对TC18钛合金动态力学性能的研究很少，大部分研究是在准静态条件下进行的。在准静态条件下，由于加载非常缓慢，材料因塑性变形产生的热量能够及时传递出去，材料的塑性变形为一个等温过程，但在冲击载荷下，由于冲击时间很短，塑性变形所产生的热量来不及传递散发出去，因此这种情况下的塑性变形为绝热过程。很明显，冲击加载下，材料的应变率、温度、应变和绝热温升与材料的塑性变形是耦合在一起的，正确理解它们之间的耦合作用对预测材料的塑性变形行为是非常重要的。几十年来，人们一直致力于以材料模型的形式确定材料的变形行为，即通过建立本构模型对其力学性能进行表征。材料的本构模型即本构关系，是指材料的流变应力与变形温度、应变率以及变形程度之间的关系。本构关系也是有限元软件对材料变形过程进行数值仿真的重要基础，它是对材料性能的最基本表征[12]。在不同的变形条件下，不同的材料有着不同的本构关系[13]，它是结构或材料宏观力学性能的综合反映，能够反映物质宏观性质的数学模型。

材料的本构模型一般可以分为2类：一类为物理基础的本构模型，一类为经验或半经验的本构模型，相较于物理模型，经验或半经验模型可以通过有限的物理实验采用较少的材料参数来表征材料的力学性能。J-C模型即为典型的经验模型，由于其同时考虑了材料的应变率硬化和热软化效应，被广泛用来表征材料在高温和高应变率下的变形行为。

本研究拟在准静态实验的基础上，得到TC18钛合金在准静态下的塑性屈服强度，以此为依据选择霍普金森压杆型号，进行不同温度及应变率下的冲击加载实验，从而得到该合金在不同工况下的力学性能，并以实验数据为基础，采用J-C模型进行力学性能表征，通过实验数据分别确定模型中的应变率项和温度项参数，最终得到TC18钛合金在高温和冲击载荷共同作用下的塑性本构方程，并与实验结果进行对比验证，以期为TC18钛合金的有限元模拟奠定基础，同时为合金的结构设计和优化提供依据。

1 实 验

1.1 试样制备

本试验中所用的 TC18钛合金棒材由宝鸡钛业股份有限公司提供，化学成分见表1。根据试验设备的相关参数及应变率范围，选取动态试验试样尺寸为φ6 mm×6 mm。

表1 TC18 钛合金棒材的化学成分(w/%)

1.2 实验方案

TC18钛合金动态力学性能实验是在分离式Hopkinson压杆(φ13 mm)上进行的。由于试件的屈服强度相对较大，为1 060 MPa，高速冲击时需要较高的能量，而且要使分离式Hopkinson压杆在工作时处于弹性阶段，所以进行高应变率实验比较困难。本次实验拟测试TC18钛合金在应变率分别为500、1 000、1 500 s-1，温度分别为298、523、773、1 023 K的动态压缩行为。为了保证实验结果的可重复性，每个应变率下至少进行2次试验，取比较相近的2组实验结果的平均值作为最终实验结果。

2 J-C本构模型构造

TC18钛合金的组织类型为α+β型，非常适合采用J-C模型来表征其在冲击荷载下的力学性能[14]。J-C模型考虑了温度、应变率和应变等因素，形式简单，具有清晰的物理解释，同时参数较少，比较容易求解。J-C模型适用于描述金属材料从低应变率到高应变率下的动态行为，甚至可以用于准静态实验结果的分析，其基本表达式为：

(1)

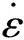
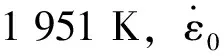
2.1 采用J-C模型表征准静态力学性能

σ=A+Bεn

(2)

将TC18钛合金近似为线性强化弹塑性材料，根据准静态实验数据，可以得出屈服应力为1 060 MPa，即A为1 060 MPa，代入式(2)得：

σ-1 060=Bεn

(3)

令：

Y=σ-1 060，X=ε

(4)

应用最小二乘法拟合方程，得到式(5)：

Y=1 883.7X0.895 5

(5)

即B、n分别为 1 883.7和0.895 5。将式(5)代入式(2)得到式(6)：

σ=1 060+1 883.7ε0.895 5

(6)

将由式(6)计算的数据和准静态下的实验曲线进行对比，结果如图1所示。

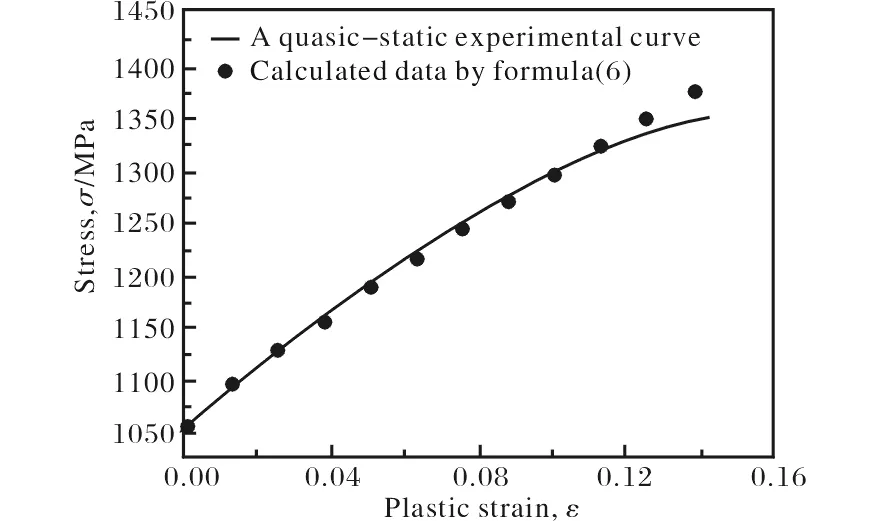
图1 式(6)计算数据与准静态下应力-应变曲线的对比图Fig.1 Comparison diagram of calculated data by formula(6) and a quasi-static stress-strain curve

从图1可以看出，式(6)的计算数值不能很好的拟合实验曲线。经反复拟合对比，发现对于TC18钛合金而言，一元二次方程比幂函数更符合实验曲线的增长趋势，为了更好的对实验数据进行拟合，将式(3)改写为式(7)：

σ-1 060=λ1ε2+λ2ε+λ3

(7)

由式(4)在坐标系下应用最小二乘法拟合方程，得到式(8)：

Y=-6 882.3X2+3 094.3X-1.652 8

(8)

将式(8)代入式(7)得式(9)：

σ= 1 060 - 6 882.3ε2+ 3 094.3ε- 1.652 8

(9)

将由式(9)计算的数据和准静态下的实验曲线进行对比，结果如图2所示。通过图1与图2对比可以看出，式(9)与实验曲线更为接近，因此采用式(9)能够更好的表征TC18钛合金在准静态下的塑性力学行为。

图2 式(9)计算数据与准静态下应力-应变曲线的对比图Fig.2 Comparison diagram of calculated data by formula(9) and a quasi-static stress-strain curve

2.2 采用J-C模型表征动态力学性能

2.2.1 确定J-C模型中应变率项

在常温下，J-C本构方程可以简化为式(10)：

(10)

(11)

使用最小二乘法对参数进行拟合得到C为0.046 4，将数值代入式(10)得到式(12)：

(12)

由于常温下，TC18钛合金的动态塑性流变应力未随着应变的增加而增长，趋势接近于平稳，因此在方程中不考虑应变项，只考虑应变率项，故得到的常温下TC18钛合金的动态本构方程如式(12)所示。

将由式(12)计算的数据和常温动态下的实验曲线进行对比，结果如图3所示。从图3可以看出，式(12)可以很好的预测TC18钛合金在常温冲击载荷下的流变应力。

2.2.2 确定J-C模型中温度项

通过温度为523、773、1 023 K，应变率为500、1 000、1 500 s-1的动态实验应力-应变曲线(共9组数据)来拟合m。

在高温下，J-C本构方程可以简化为式(13)：

(13)

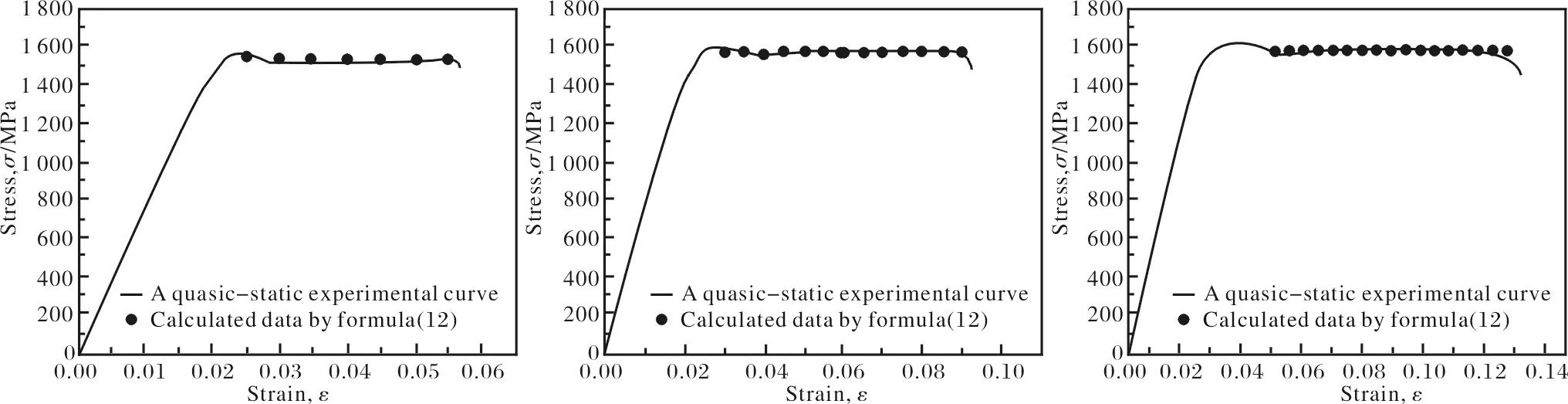
图3 式(12)计算数据与常温动态应力-应变曲线的对比图Fig.3 Comparison diagrams of calculated data by formula(12) and dynamic experimental stress-strain curves at normal temperature:(a)500 s-1;(b)1 000 s-1;(c)1 500 s-1

式中：σ(T*)为高温下合金的屈服应力，σ(Tr)为参考温度下合金的屈服应力。

将式(13)两边取对数得式(14)：

(14)

式中：Tr为298 K，Tm为1 951 K。令：

(15)

使用最小二乘法对参数进行拟合，得到m=0.85，代入(13)得式(16)：

(16)

在高温下，TC18钛合金动态塑性流变应力随应变的增加变化很小，趋势接近于平稳，因此在方程中亦不考虑应变项，只考虑应变率项和温度项，故得到的高温与冲击载荷共同作用下TC18钛合金的本构方程如式(16)所示。将由式(16)计算的数据与高温动态下的实验曲线进行对比，结果如图4所示。从图4可以看出，式(16)可以较好的预测TC18钛合金在高温与冲击载荷共同作用下的塑性流变应力。

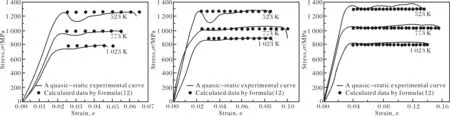
图4 式(16)计算数据与高温动态应力-应变曲线的对比图Fig.4 Comparison diagrams of calculated data by formula(16) and dynamic experimental stress-strain curves at high temperatures：(a)500 s-1；(b)1 000 s-1；(c)1 500 s-1

3 结 论

基于实验数据，建立了TC18钛合金在高温与冲击载荷共同作用下的塑性本构方程：

通过对确定的本构方程的计算结果和实验结果进行对比，表明该模型可以较好地预测TC18钛合金在高温与冲击载荷共同作用下的塑性流变应力。