基于马氏距离的重采样方法在流量识别中的应用❋
时鸿涛, 李洪平, 刘 竞
(中国海洋大学信息工程学院, 山东 青岛 266100)
精确的网络流量识别是流量工程、网络安全、网络质量服务(QOS)以及用户行为分析等工作的基础[1]。由于动态传输技术、流量加密算法和隧道技术在互联网中的广泛应用,传统的基于端口号和有效载荷检测的流量识别技术变得不再准确和高效,因此人们提出了基于机器学习的流量识别算法[2]。这类算法通过分析和识别流量底层的统计特征来实现网络流量的识别。由于不需要分析流量的有效载荷信息,这类算法的计算性能和准确率都非常高。目前,基于机器学习的流量识别方法已经成为了网络流量研究的重点。然而,随着研究的深入,人们发现网络流量中数据分布的不均衡问题会严重影响流量识别的准确率。这种不均衡通常会导致机器学习算法偏向于流量数据中多数类的流量样本。例如:文献[3]指出网络流量数据中HTTP流量的数量通常会远远超过P2P和VoIP流量的数量,而机器学习算法通常会将所有流量识别为HTTP流量以实现高准确率。在这种情况下,机器学习算法对于少数类流量的识别准确率非常低。然而,在许多情况下这些少数类流量(例如P2P和VoIP流量)却是人们更加关心的。
目前,解决数据分布不均衡问题的方法可以主要地分为两个方向:数据层方法和算法层方法。数据层方法主要通过对不均衡数据中的少数类进行过采样或者对多数类进行欠采样来实现数据的均衡。文献[4]提出了一种新的过采样方法SMOTE(Synthetic minority over-sampling technique),该方法能够通过合成新的样本来提高少数类样本的比例。文献[5]提出了一种边界SMOTE过采样方法,该方法通过对边界附近的少数类样本进行过采样来实现样本的均衡。文献[6]通过比较过采样方法和欠采样方法,指出过采样方法在解决数据分布不均衡问题时比欠采样方法更加有效。此外,算法层方法主要通过调整与错误分类相关的偏差来解决数据分布不均衡问题。文献[7]通过使用样本加权方法来构建成本敏感决策树(Cost-sensitive decision tree)以解决数据分布不均衡问题,并且该方法被证明能够非常有效的解决数据分布不均衡问题。文献[8]比较了成本敏感方法和重采样方法在解决数据分布不均衡问题的效果,结果显示成本敏感方法能够实现与重采样方法相似的效果。然而,以上方法虽然取得不错的效果,但这些方法主要用于二分类的数据分布不均衡问题,对于网络流量中的多分类数据分布不均衡问题,现有的重采样方法往往存在过拟合的缺点,而成本敏感方法则由于难以获得准确的错误分类偏差从而导致较低的识别准确率。
本文针对以上存在的问题,提出了一种基于马氏距离的重采样算法,该方法能够兼顾数据分布结构和变量间的相关性。因此所生的样本能够保留原始数据分布特征,并最大程度地避免过拟合的发生。
1 算法模型
1.1 马氏距离度量方法
马氏距离是由印度学者马哈拉诺比斯提出的一种距离度量方法,该方法能够有效的计算两个向量之间的相似度距离。相比欧氏距离,马氏距离能够考虑到向量中各变量之间的相关性。欧氏距离是一种普遍采用的距离度量方法,它被定义为n维空间中两个向量之间的几何距离,其计算公式如下:
(1)
也可以通过向量运算形式来表示:
(2)
欧氏距离的特点是计算向量之间的平均几何距离,即向量中每个变量对于欧氏距离的贡献是相同的。然而,在统计学中人们更倾向于根据向量中每个变量的方差来评估变量间的距离,并且具有较大方差的变量在距离计算中将具有较高的权重。因此,马氏距离度量更能体现这一统计特性。马氏距离的计算公式可表示如下:
(3)
式中:S为样本集的协方差矩阵;因此,马氏距离能够兼顾数据分布特征和变量之间的相关性。值得注意的是,当协方差矩阵S为单位矩阵时,马氏距离可简化为欧氏距离。
1.2 主成分分析介绍
主成分分析是一种的多元统计方法,它能够在降低数据维度的同时尽可能的保留原始数据中的大多数变量信息。该方法主要通过线性转换将一组存在相关性的变量转换为一组线性无关的综合变量,这些转换后的综合变量被称为主成分。主成分分析的公式可表示如下:
C=AX
。
(4)
式中:X为样本数据矩阵;A为主成分系数矩阵;C为主成分向量,且主成分之间相关性为零,即Cov(Ci,Cj)=0 (Ci,Cj∈C,i≠j)。因此,主成分之间的协方差矩阵可表示为一个对角矩阵V,其公式如下:
V=λE。
(5)
式中:λ是主成分的特征值向量,E为单位矩阵。
此外,为了简化原始数据,在选择主成分数量时通常会选择一个主成分集合的子集来代表原始变量。通常主成分个数的选择需要根据所选主成分的方差累计贡献率G来决定。
(6)
式中:λ为各主成分的特征值;s为所选择的主成分数量;n为全部主成分数量。当方差累积贡献率G>85%时,就认为所选择的前s个主成分能够反映原始变量的信息。
1.3 基于马氏距离的重采样方法
本文所提出的基于马氏距离的重采样方法将根据少数类中每个样本点与样本集中心之间的马氏距离来生成新的合成样本。由于马氏距离计算的复杂性,本文先利用主成分分析将原始样本数据转换到主成分空间,再通过计算各样本点到样本集中心的马氏距离来实现新样本的生成。主成分空间下马氏距离的计算公式可简化为
(7)
即:
(8)
本文将利用公式(8)来实现样本数据的重采样,整个算法流程如算法1所示。基于马氏距离的重采样算法主要包含以下几个步骤:
(1)对输入的样本数据进行零均值化处理(代码1)。
(2)使用主成分分析方法将零均值化后的样本数据转换至主成分空间,并选择方差累积贡献率G>85%的主成分子集作为原始变量的代表以简化计算复杂度(代码2)。
(3)在主成分空间中循环生成新样本(代码3)。首先,随机选择一个样本数据p,计算它到样本集中心的马氏距离dM(p,0)(代码3.1),然后,定义一个新的样本数据q,并使该样本数据满足条件dM(q,0)=dM(p,0)(代码3.2)。
(4)使用主成分分析方法将生成的新样本集合转换至原始数据空间(代码4)。
(5)通过逆零均值化得到最终数据结果(代码5)。
(6)对所有新样本数据进行输出(代码6)。
算法1基于马氏距离的重采样算法
输入:Sin={(x1,1,x1,2,…,x1,m),…,(xn,1,xn,2,…,xn,m)} %少数类样本集合,
k%需要生成的新样本数量,
输出:Sout%新生成的样本集合。
1:forj=1 tomdo
end for
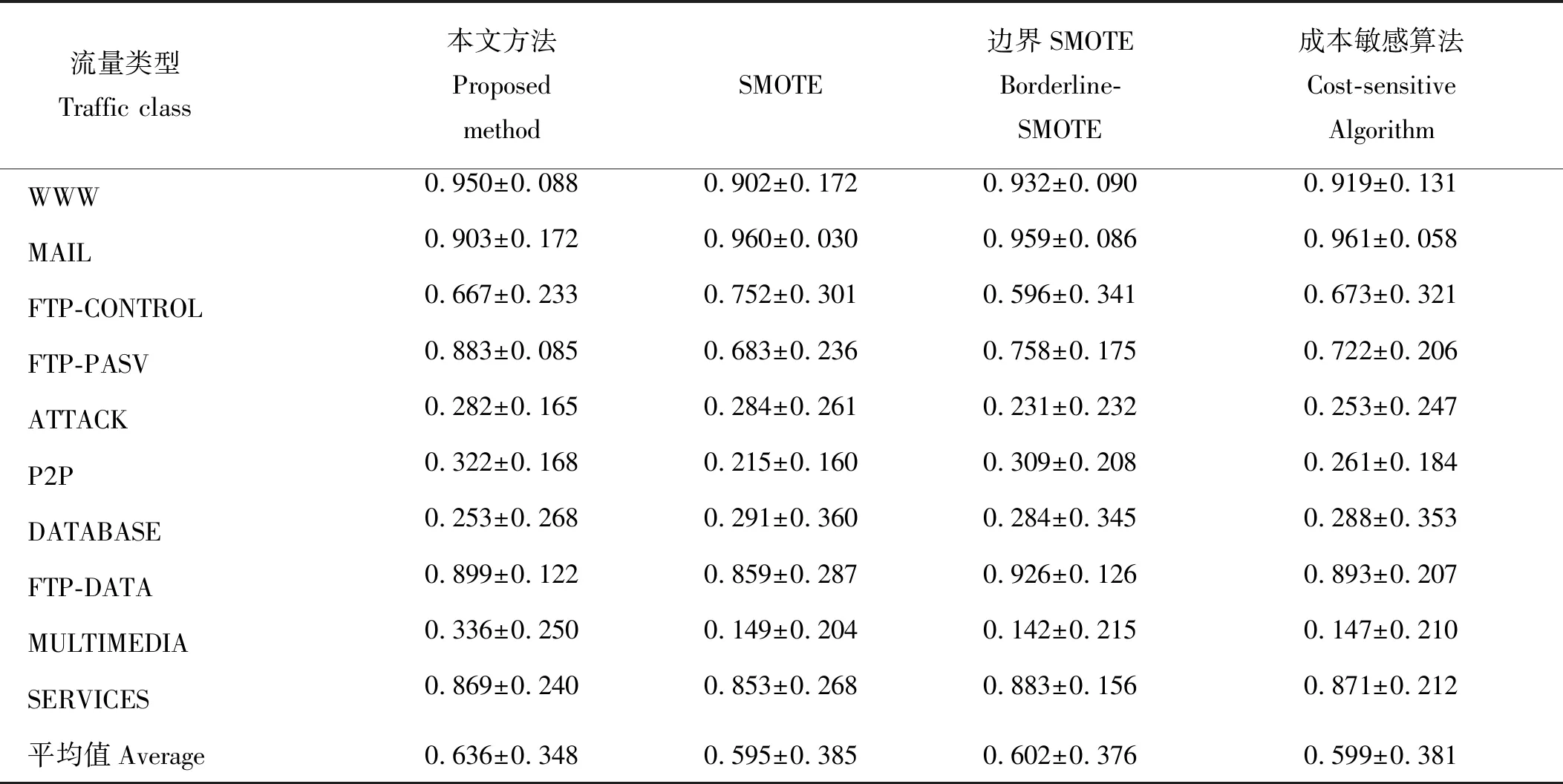
2:计算Z的主成分,并选择G>85%的主成分子集T,其行数和列数分别为n和m1(m1 3:fori=1 tokdo 3.1:p=random(T) 3.2:定义q forj=1 tom1-1 do %为q前m-1项赋值。 qj=random(-λ1dM,λidM) end for 将q加入集合Tnew。 end for 4:将Tnew转换至原始数据空间,得到新集合Znew。 6:返回Sout。 通过以上算法,所有新生成的样本将与原始样本保持相同的数据分布特征。下面将通过实验来验证本文算法的效果。 为了检验本文提出的重采样方法,本文使用剑桥大学实验室提供的公共网络流量数据[7]作为实验数据。这些网络流量数据包含10个数据集合,每个集合包含有不同数量的网络流量样本。每个样本具有248个特征,这些特征是通过使用Tcptrace进行提取。实验数据的流量特征信息如表1所示。从表1中可以发现对于所有集合,WWW流量类型的样本数量远远超过其他流量类型。因此,这些数据集都存在明显的多分类数据分布不均衡问题。 表1 实验数据特征信息Table 1 The characteristic information of the experimental data 为了评价所提出方法的有效性,本文使用3种不同的评价指标对分类结果进行分析。这些评价指标包括总体准确率(Overall Accuracy, OA)、F-measure和g-mean。这些指标通常被用于评价信息分类和检索的效果。 令TP代表真阳,TN代表真阴,FP代表假阳,FN代表假阴。OA可以表示为被正确分类的样本数量与全部样本数量之间的百分比,它反映了分类结果的总体正确程度,OA越高表示被正确分类的样本数量越多,其公式如下: (9) F-measure是召回率R和精确率P的一种加权平均值,它表示了对分类结果中的查准率和查全率的综合评价,F-measure越高表示分类算法更加有效: (10) g-mean表示为所有类型流量召回率的几何平均值,它主要用于评估多分类分布不均衡数据的分类效果,g-mean越高表示对少数类的分类效果越好: (11) 式中n为网络流量类型的数量。 在本文中,所有指标将分别按照网络流量数据的流(Flow)和字节(Byte)两种方式进行计算以评估本文方法的性能。 本文选用C4.5决策树作为分类算法,使用数据集1作为训练数据,并对其余9个数据集进行分类实验。为了证明本文方法的有效性,本文方法将与文献[2]中的SMOTE方法,文献[3]中的边界SMOTE方法以及文献[8]中的基于MetaCost的成本敏感算法进行比较,总体实验结果如图1所示。通过对图1的观察,我们发现本文方法对于流OA、字节OA和流g-mean都获得了最佳分类结果,然而对于字节g-mean,本文方法的性能略低于其他方法。此外,我们发现在本实验中边界SMOTE方法的实验结果要优于SMOTE方法,这与文献[3]中的结论一致。相比之下,成本敏感算法得到了最差的实验结果。 图1 总体实验结果Fig.1 Overall experimental results 表2详细显示了4种方法对于各流量类型所获得的流F-measure。通过表2不难发现本文方法对于大多数流量类型均取得了最佳的流F-measure,而对于ATTACK和FTP-DATA流量类型,本文方法所取得的流F-measure也接近于相应的最佳流F-measure。此外,通过对表3中最后一行所显示的平均流F-measure进行分析,可以证明本文方法获得了最佳的流分类效果。 表3详细显示了4种方法对于各流量类型所获得的字节F-measure。与表2类似,本文方法对于大多数流量类型,特别是含有大象流(Elephant flow)的流量类型(如:P2P和FTP-Data流量类型),均获得了最佳的字节F-measure。此外,通过对表3中最后一行所显示的平均字节F-measure进行分析,可以证明本文方法获得了最佳的字节分类效果。 表2 4种方法对于各网络流类型所获得的流F-measureTable 2 The flow F-measure of the four methods for each traffic class 通过对全部实验结果进行分析,可以发现本文方法在处理网络流量中的多分类数据分布不均衡的问题时,其性能明显优于现有的重采样方法以及成本敏感方法,这也充分证明了本文方法在生成新的少数类样本时能够充分保留原始数据中的数据分布特征,从而最大程度地避免破坏原始样本数据的数据结构。 表3 4种方法对于各网络流类型所获得的字节F-measureTable 3 The byte F-measure of the four methods for each traffic class 本文提出了一种基于马氏距离的重采样方法,该方法能够根据样本数据到样本集合中心点之间的马氏距离为少数类生成新的合成样本。相比于现有的重采样方法,本文方法在为少数类生成新样本的同时,能够保持样本数据的原始分布结构,从而避免过拟合的发生。使用剑桥大学实验室提供的公共网络流量数据进行流量分类实验,实验结果证明与现有的SMOTE方法、边界SMOTE方法以及基于MetaCost的成本敏感算法相比,本文方法能够更好的提升少数类的分类准确率,从而实现最佳的流量分类效果。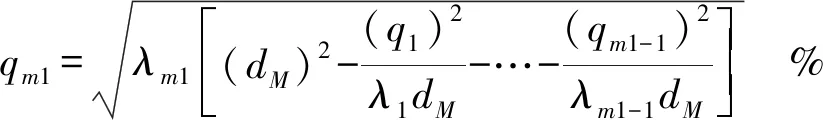
2 实验分析
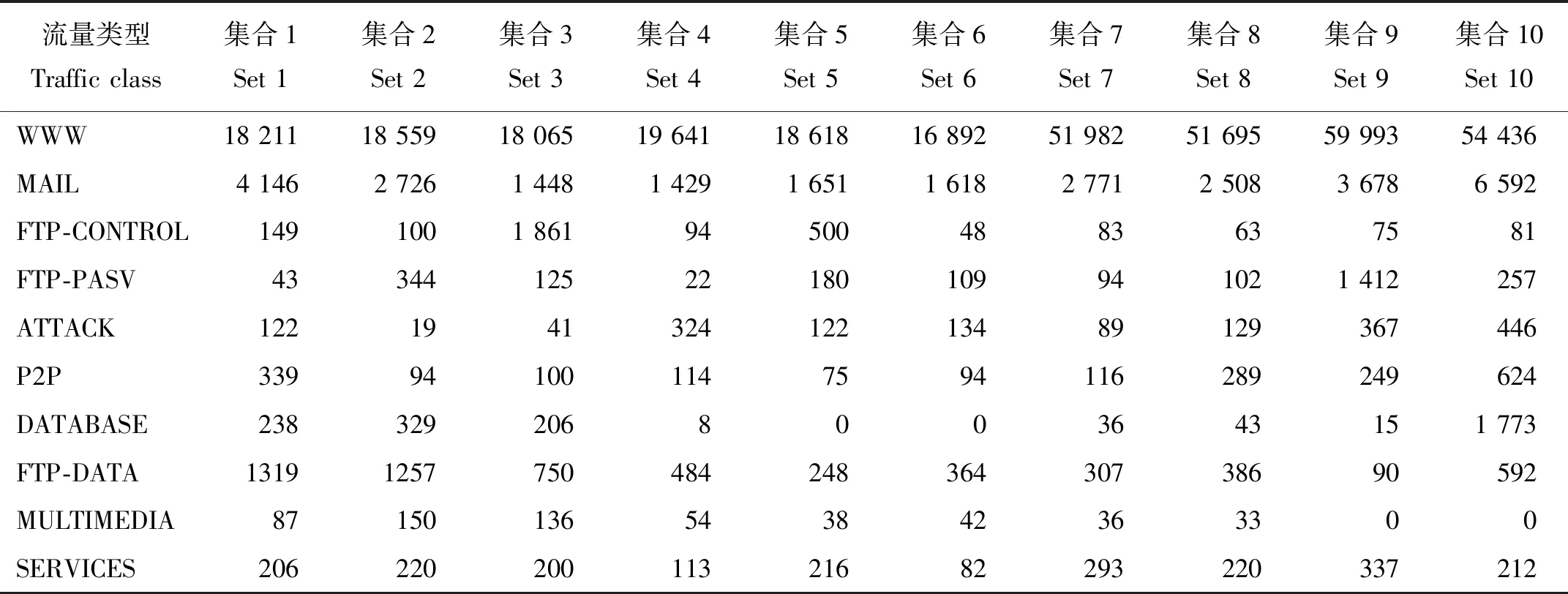
2.1 实验数据
2.2 评估指标
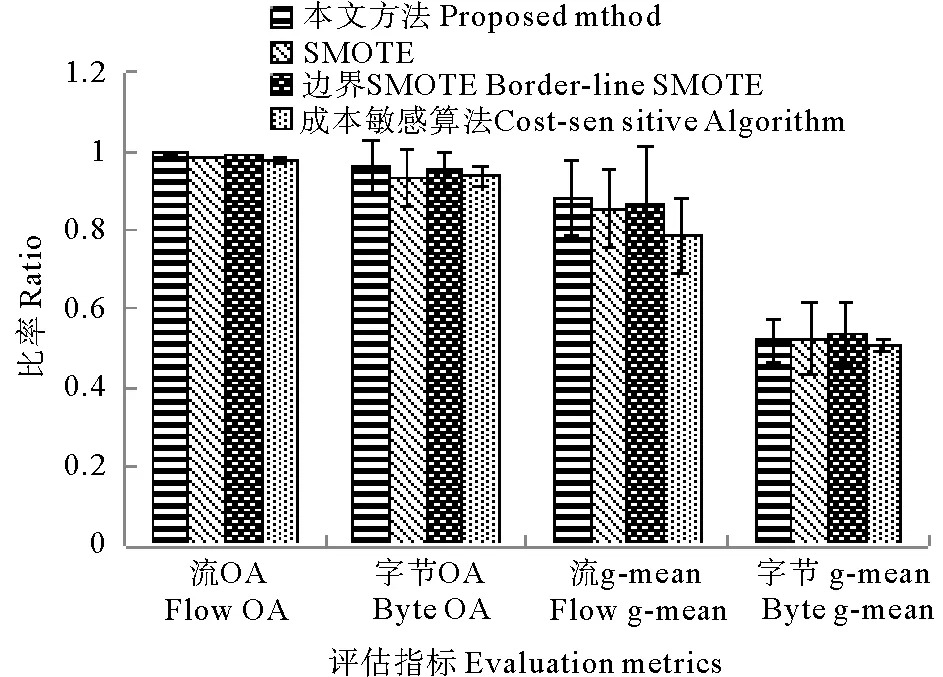
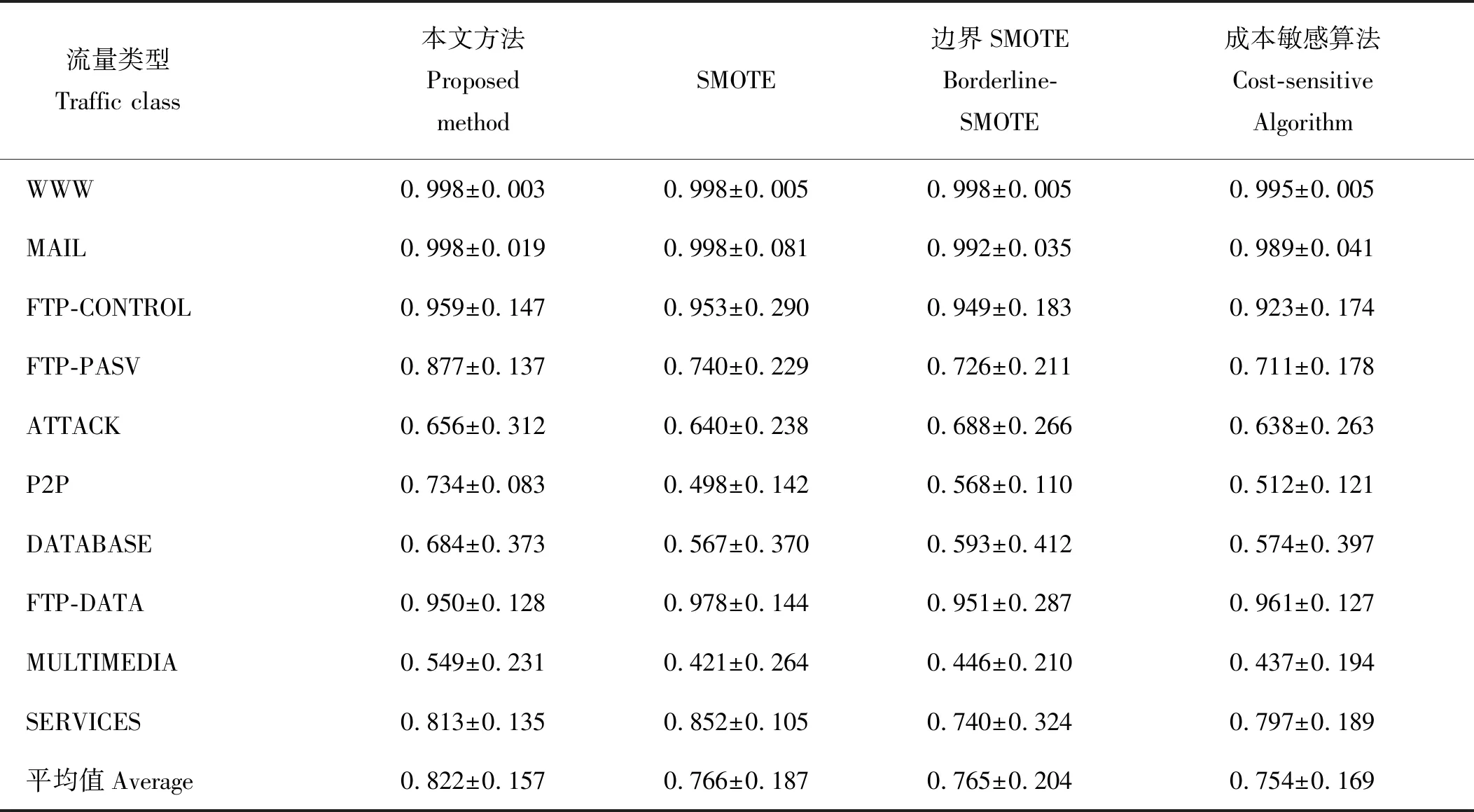
2.3 分类结果分析
3 结语

