展开与折叠 转化与互逆

在学习“展开与折叠”的过程中,可能有不少小伙伴无法在脑海中抽象出立体图形与平面图形的转化过程。其实这对我们的空间想象能力提出了较高的要求。现在我把我的一些发现整理如下,希望能帮助大家学习。
“展开与折叠”包含了两个关键词:展开、折叠,这两个词本身是一种互逆的关系。
首先,我们从图形的展开说起。展开就是将某个几何体的表面适当剪开并平铺的过程,形成的平面图形称为几何体的展开图。在小学阶段,我们曾了解到圆柱的展开图是两个圆和一个长方形(如图1)。
图1
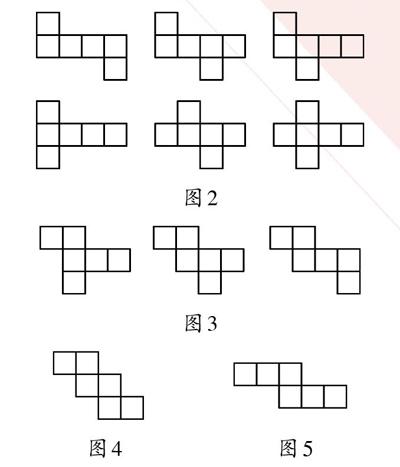
进入初中后,我们谈到图形的展开,就不得不提到一个非常重要的几何体——正方体。正方体的展开图可能是大家的一个困惑点。其实正方体的展开图种类并不多,只有11种。根据展开图中每一层的正方形个数(从上往下数),我们可以把它们分成4类,即“141型(如图2)”“231型(如图3)”“ 222型(如图4)”“33型(如图5)”。
图2
图3
图4 图5
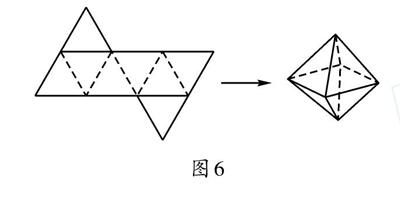
当然,在某些展开图中也隐藏着一些数量关系。比如图1中,圆的周长与矩形的长是相等的。因为如果将展开图折叠还原为圆柱,圆的一周与矩形的长是完全重合的。这里就涉及另一个关键词——折叠。将展开后的平面图形折叠成立体图形,形成几何体的过程,就是折叠。如果将8个相同的正三角形沿如图6所示的虚线折叠,则会得到一个正八面体。
图6
相较于“展开”结果的多样性,折叠结果则具有唯一性。对一个平面展开图实施不同的方法折叠,还原成几何体,这个几何体有且只有一个。在这个还原的过程中,会衍生出一类问题,比如求正方体展开图重新折叠成正方体时,原来的展开图上哪两个面是相对的?在解决这类问题之前,我们首先要明白一个基本规律:在正方体展开图中,相对的两个面不可能是“相连”的,应该是“分隔”的;如果展开图中两个面是“相连”的,那么折叠后的它们一定是相邻的面,而不是对面。
运用这个规律,我们逐个剖析,可以把正方体的11种展开图中的“对面”分布情况标注如下(如图7)。字母相同的两个面是对面。
图7
“展开”是将立体图形转化为平面图形;“折叠”是将平面图形转化为立体图形。这其中蕴含着转化和互逆的数学思想方法。我们在解决实际问题时,经常会把立体图形转化为平面图形来解决,也会借助平面图形折叠成立体图形,练习空间想象能力。
希望我的一点学习经验能为大家的学习带来帮助。
教师点评
“展开与折叠”是苏科版《数学》教材七年级上册的学习内容,是在小学内容的基础上对图形的进一步认识。在小学阶段,同学们已经初步认识了正方体、圆柱、圆锥等立体图形,从直观上對展开与折叠有了一定的认识,但对展开与折叠前后立体图形与平面图形的位置、数量之间的关系认识不足,直观想象能力有待进一步训练提高。许辰宇同学在平时的学习中,注重自主探索,及时归纳、总结学习中的小规律、小发现,形成有借鉴意义的小成果,值得同学们学习。众所周知,正方体与其展开图之间的相互转化是学习的重点,许辰宇同学以最具代表性的“正方体”为例,归纳总结了4类共11种展开图,便于记忆使用。文章最后给出正方体展开图的互为对面情况的标记,有助于同学们探寻对面的规律,理解并掌握展开图的特征。相信他的这篇小文章会对同学们的图形学习有一定的帮助。
(指导教师:孙 凯)

