“图形的运动”错解剖析

王云峰

图形的运动有三种方式：平移、翻折、旋转，习惯上分别将它们称为平移变换、对称变换、旋转变换。初学这部分内容，同学们常因观察不仔细，想象不丰富，思考不全面等原因出错。下面我们举例说明。

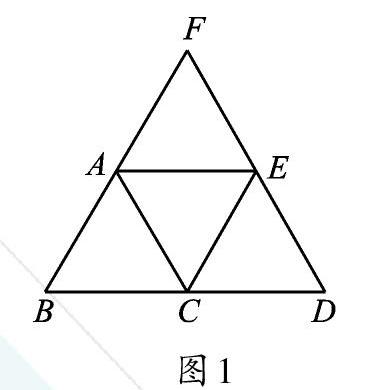
例1 如图1，4个小三角形的形状与大小都相同，其中可以通过平移三角形ABC而得到的三角形一共有（）。

A.0个 B.1个 C.2个 D.3个

图1 图2

【错解】D。

【错因】有些同学由条件“4个小三角形的形状与大小都相同”，误认为这4个三角形可以通过相互平移得到，错在没有考虑平移的方向。实际上，三角形ACE是由三角形ABC沿AC翻折得到的。

【正解】C。

【点评】两个图形间的运动方式为平移变换，它们不仅形状、大小相同，而且方向也要一致;翻折变换实际上是反向平移。

例2 “飞流直下三千尺”“坐地日行八万里（只考虑地球自转）”，如果只从数学角度看，它们分别蕴含的图形变换是（）。

A.平移、平移 B.平移、翻折

C.平移、旋转 D.旋转、翻折

【错解】A。

【错因】一些同学是这样思考的：人在地面行走可看成是平移变换，因此从数学角度看，“坐地日行八万里”是平移变换。其错在没有关注括号中的条件“只考虑地球自转”。它表达的意思是：人在地球上不动（“坐地”），地球自转导致人“日行八万里”。因此这是旋转变换。

【正解】C。

【点评】审题要仔细、全面，要关注题中的每一个条件。数学中许多式子会采用括号的形式表示，若不考虑全面，则容易出错。如：n=a（a≥0）写成n=a，就是错的。

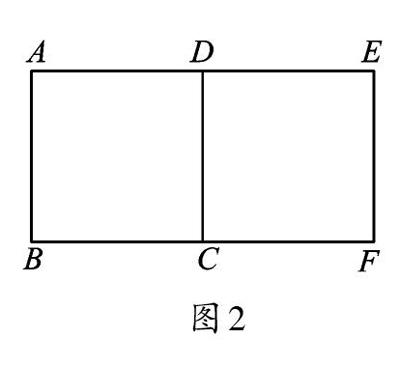
例3 如图2，正方形ABCD绕某个点（记为点O）旋转后能与正方形CDEF重合，则点O的位置有个。

【错解】2。

【错因】一些同学观察图形，发现点O在点C（或点D）处时，正方形ABCD旋转后能与正方形CDEF重合，错在仅关注了图中有字母的点，忽视了其他的点。实际上，绕CD的中点旋转，正方形ABCD旋转后也能与正方形CDEF重合。

【正解】3。

【点评】由图形的位置可知，正方形ABCD绕点C（或点D）旋转90°能与正方形CDEF重合。考虑完这种情形后，再考虑旋转90°的整数倍后结论是否也成立，这是解答这类问题的一个重要策略，可防止出现遗漏。绕CD的中点将正方形ABCD旋转180°能与正方形CDEF重合。

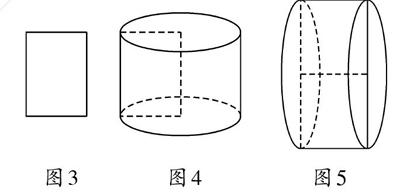
例4 如图3，是一个长为4cm、宽为3cm的长方形纸片。若将此长方形纸片绕边所在的直线旋转一周，求所形成的几何体的体积。

图3图4 图5

【错解】如圖4，是长方形纸片绕一边所在的直线旋转一周形成的几何体，这是一个圆柱，它的底面半径为3，高为4，所以它的体积为π×32×4=36π。

【错因】审题不清。“将此长方形纸片绕边所在的直线旋转一周”并没有指明是绕长边旋转还是绕短边旋转，因此要分两种情形求解。

【正解】当长方形纸片绕长边旋转一周，如图4，它的体积为36π。

当长方形纸片绕短边旋转一周，如图5，这个几何体是圆柱，它的底面半径为4，高为3，所以它的体积为π×42×3=48π。

综上，所求几何体的体积为36π或48π。

【点评】对于没有指明对象的问题，要考虑进行分类讨论。

例5 图6是3×3正方形方格，将其中两个方格涂黑，并且使得涂黑后的整个图案沿某条直线翻折，直线两旁的部分重合。约定正方形ABCD绕某点旋转能重合的图案都视为同一种图案，如图7中的四幅图就视为同一种图案。则得到的不同图案共有（）。

A.4种 B.5种 C.6种 D.7种

图6 图7

【错解】B。

【错因】一些同学设计的图案如图8所示，忽视了题目中范例的情形。根据题意，范例也应当包含在答案中。

图8

【正解】C。

【点评】利用翻折设计图案，可先确定所有可能的“折线”，然后在“折线”的两侧进行设计。本题的图案是正方形，而正方形的“折线”有4条，如图9所示。由于第1、2个图绕某点旋转重合，第3、4个图绕某点旋转也重合，所以只需在第1、3个图中设计即可。由第1个图可设计出范例及图8中前两个，由第3个图可设计出图8中后三个。这样就能防止出现遗漏了。

图9

（作者单位：江苏省盐城市葛武初级中学）